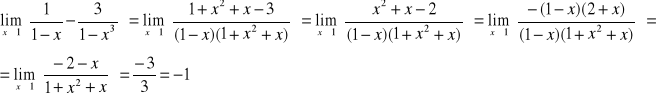
1. Obliczyć granice funkcji.

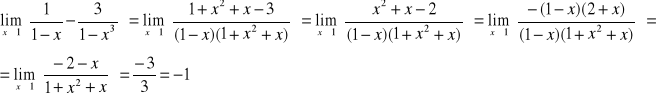
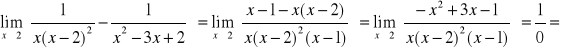
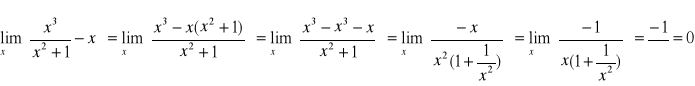
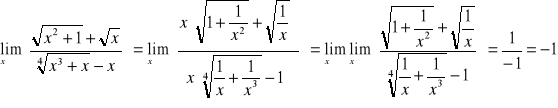
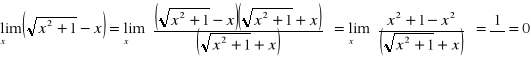
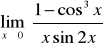
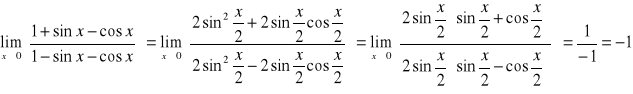
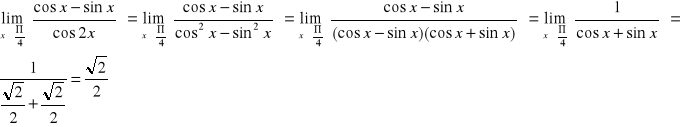
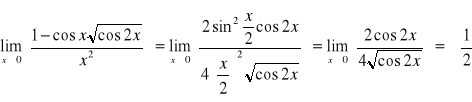
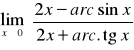
2. Obliczyć pochodne funkcji.

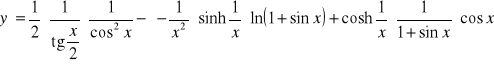
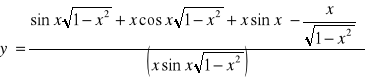
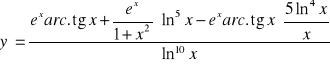
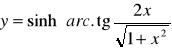
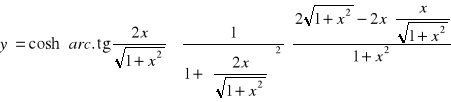
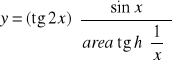
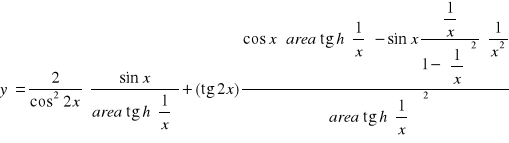
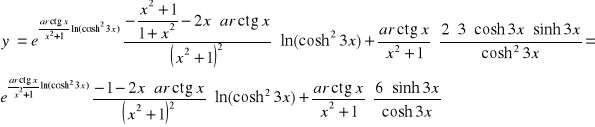
3. Wykazać że funkcja y=y(x) spełnia równanie.

a)

b)

c)

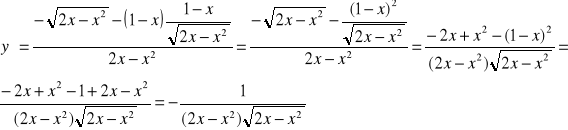
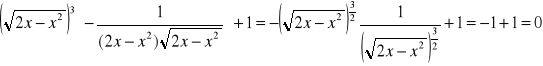
4. Obliczyć granice funkcji

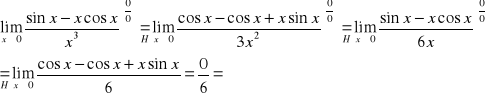
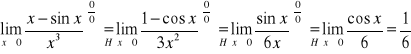
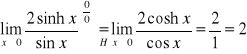
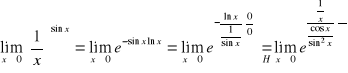
5. Podaj własności funkcji

a)

D: x∈R

PD: y∈R

Funkcja nie posiada ekstramum lokalnego Δ<0 i jest rosnąca dla x∈R.

x₀=1

Funkcja posiada punkt przegięcia w punkcie x₀=1, jest wypukła w przedziale x∈(-∝;1) i wklęsła w przedziale

x∈(1;∝).

b)

D: x∈R

PD: y∈<0, ∝)

x₀=0

Funkcja posiada ekstremum lokalne w punkcie x₀=0 i jest rosnąca dla x>0 i malejąca dla x<0.

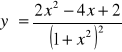
Funkcja posiada punkt przegięcia w punkcie x₀=1, jest wypukła dla x∈R.

c)

D: x∈R

PD: y∈R

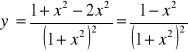
x₁=-1 ; x₂=1

Funkcja posiada ekstremum lokalne w punkcie x₁=-1 i x₂=1 oraz jest rosnąca dla x∈(-1;1) i malejąca dla x∈(-∝;-1)∪ (1;∝).

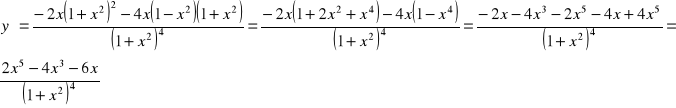
x₀=0

Funkcja posiada punkt przegięcia w punkcie x₀=0, jest wklęsła dla x<0 i wypukła dla x>0.