2.1. Zmienne losowe, ich rozkłady, dystrybuanta.

Definicja 2.2.1. Zmienną losową nazywamy dowolną funkcję
określoną w przestrzeni zdarzeń elementarnych
, przyjmującą wartości rzeczywiste i spełniającą warunki:

Warunek A. dla każdej liczby rzeczywistej
zbiór
jest zdarzeniem.

Innymi słowami funkcja
jest
— mierzalna, gdzie
, jak poprzednio, oznacza klasę zdarzeń, która jest
ciałem.

Z powyższej definicji wynika następne stwierdzenia:

Warunek B. dla każdej liczby rzeczywistej
zbiór
jest zdarzeniem;

Warunek C. dla każdej liczby rzeczywistej
zbiór
jest zdarzeniem;

Warunek D. dla każdej liczby rzeczywistej
zbiór
jest zdarzeniem.

Definicja „alternatywna”. Wartość liczbową
zależna od przypadku i taką, że dla dowolnych stałych
określone jest prawdopodobieństwo, że
przybierze wartość z przedziału
, nazywamy zmienną losową.

Definicja 2.2.2. Zmienną losową nazywamy skokową (dyskretną), jeżeli zbiór jej wartości jest skończony lub, co najwyżej przeliczalny.

Zauważmy, że kiedy przestrzeń zdarzeń elementarnych
jest skończona lub, co najwyżej przeliczalna, to zmienna losowa jest skokowa.

Definicja 2.2.3. Poznaczmy wartości zmiennej losowej skokowej przez
i oznaczmy

Definicja 2.2.4. Rozkładem zmiennej losowej skokowej nazywamy zbiór par
i dla uproszczenia rozważamy pary, gdzie
.

Definicja 2.2.5. Tablica rozkładu prawdopodobieństwa

Definicja 2.2.6. Zmienną losową jest ciągła, jeżeli istnieje taka nieujemna i całkowalna w przedziale
funkcja
, że dla dowolnej wartości
możemy oznaczyć

.

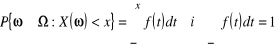
Definicja 2.2.7. Funkcję
nazywamy gęstością prawdopodobieństwa zmiennej losowej ciągłej.

Zauważmy, że
, mimo to, że nie jest to zdarzenie niemożliwe.

Definicja 2.2.8. Zdarzenie, że zmienna losowa
(skokowa lub ciągła) przyjmuje wartość mniejszą niż
, nazywamy dystrybuantą zmiennej losowej
, tzn.

.

Zaznaczmy, że dla zmiennej losowej skokowej

,

a dla ciągłej

.

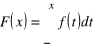
Różniczkując funkcję
w punktach ciągłości otrzymujemy

.

Dystrybuantą dowolnej zmiennej losowej
jest funkcją niemalejącą, przynajmniej lewostronne ciągłą, oraz spełnia warunki

.

Przy czym w przypadku zmiennej losowej ciągłej można korzystać z nierówności
,
lub
.

Przykład 2.2.1. Dobrać tak stałą
, by funkcja

była gęstością prawdopodobieństwa. Wyznaczyć dystrybuantę i obliczyć
.

Przykład 2.2.2. Zmienna losowa ma rozkład o dystrybuancie

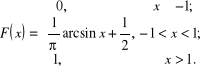
Wyznaczyć gęstość i obliczyć
.

Przykład 2.2.3. Zmienna losowa ma rozkład prawdopodobieństwa o gęstości

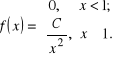
Wyznaczyć stałą
, dystrybuantę, obliczyć
w jednym doświadczeniu i prawdopodobieństwo tego, że w trzech doświadczeniach zmienna losowa ani razy nie przyjmie wartości z przedziału
.

2.2. Wartość przeciętna, momenty, wariancja zmiennej losowej.

Definicja 2.2.1. Wartością przeciętną zmiennej losowej skokowej nazywamy

,

a ciągłej

.

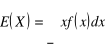
Definicja 2.2.2. Momentem zwykłym
rzędu
zmiennej losowej
nazywamy wartość przeciętną zmiennej losowej
, tzn. dla zmiennej losowej skokowej mamy

,

a dla ciągłej

.

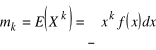
Definicja 2.2.3. Zmienną losową scentrowaną
lub odchyleniem zmiennej losowej
nazywamy

.

Definicja 2.2.4. Wariancja
(lub
) zmiennej losowej
nazywamy moment zwykły rzędu drugiego zmiennej losowej
, tzn.

.

Zaznaczmy, że bezpośrednio z poprzednich definicji również mamy

.

Dla zmiennej losowej skokowej
zapisujemy także

.

Jeśli
, to

.

Jeżeli zmienna losowa
zostanie poddana dowolnemu przekształceniu liniowemu
, gdzie
i
— stałe rzeczywiste, to

oraz
.

Definicja 2.2.5. Odchyleniem standardowym
zmiennej losowej
nazywamy

Definicja 2.2.6. Zmienną losową standardową (unormowaną) nazywamy

Dla tej zmiennej mamy

.

Przykład 2.2.1. Zmienna losowa ma rozkład o gęstości

Obliczyć
, wyznaczyć dystrybuantę, obliczyć
.

Przykład 2.2.2. Rzucamy monety 4 razy. Niech zmienna losowa
przyjmuje wartości równe liczbie wyrzuconych orłów. Podać rozkład tej zmiennej losowej i obliczyć
, wyznaczyć dystrybuantę, obliczyć
.

Przykład 2.2.3. Gracz rzuca raz kostką i otrzymuje 1 zł, gdy wyrzuci parzystą liczbę oczek, 2 zł, gdy wyrzuci 5 oczek, a w pozostałych przypadkach przegrywa 3 zł. Podać rozkład zmiennej losowej
, która jest wygrana gracza, wyznaczyć wartość przeciętną
i odpowiedzieć na pytanie, czy jest ta gra sprawiedliwa, tj. czy
?

Przykład 2.2.4. Dystrybuanta zmiennej losowej
określona jest wzorem

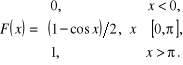
Znaleźć gęstość, obliczyć
, wyznaczyć
.

2.3. Rozstęp, mediana, moda.

Dla zmiennej losowej skokowej
przyjmującej znaczenia
, za miarę rozproszenia przyjmuje się też tzw. rozstęp
, definiowany za pomocą wzoru

,

gdzie
i
.

Medianą (wartością środkową)
zmiennej losowej ciągłej
tu wartość
, dla której dystrybuanta równia się
, tzn.

(albo
i
).

Innymi słowami mediana jest pierwiastkiem równania

.

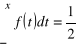
Zaznaczmy, że mediana może przyjmować nieskończenie wiele wartości.

Mediana jest szczególnym przypadkiem tzw. parametrów pozycyjnych jeszcze zwanych kwantylami.

Definicja 2.3.*. Kwantylem rzędu
zmiennej losowej
nazywamy wartość
, taką, że

i
.

Przy tym górnym kwantylem nazywamy kwantyl dla
, a wówczas dolnym kwantylem — kwantyl dla
. Kwantyle dla
nazywamy decylami.

Modą (wartością modalną, dominantą)
zmiennej losowej ciągłej
nazywamy tu wartość
, dla której gęstość
lokalnie przyjmuje wartość maksymalną. W przypadku różniczkowalnej funkcji gęstości
mamy

.

Należę zwrócić uwagę, że istnieją rozkłady antymodalne nie mające żadnej mody.

Definicja 2.3.1. Rozkład dwumianowy (Bernoulli'ego). W wyniku pewnego doświadczenia może zajść z prawdopodobieństwom
zdarzenie
(zwane za zwyczaj sukcesem) lub z prawdopodobieństwom
zdarzenie
. Dokonujemy
niezależnych doświadczeń i poszukujemy łączną liczbę sukcesów
. Mamy

,
.

Jest to rozkład dwumianowy.

Przykład 2.3.1. Zmienna losowa
ma rozkład o gęstości

Wyznaczyć dystrybuantę, obliczyć medianę i modę. Czy istnieje
?

Przykład 2.3.2. Zmienna losowa
ma rozkład o gęstości

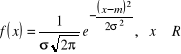
Obliczyć
, medianę i modę.

Przykład 2.3.3. Zmienna losowa
ma rozkład o gęstości

Wyznaczyć wartość stałej
, obliczyć
, medianę i modę.

Przykład 2.3.4. Zmienna losowa
ma rozkład o gęstości

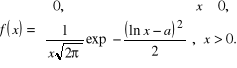
Obliczyć
.

Przykład 2.3.5. Zmienna losowa
ma rozkład dwumianowy (Bernoulli'ego) o gęstości
. Pokaż, że wartość przeciętna

.

Przykład 2.3.6. Zmienna losowa
ma rozkład dwumianowy (Bernoulli'ego) o gęstości
. Pokaż, że wariancja dla tego rozkładu

oraz
.

Twierdzenie 2.3.1. Liczba najbardziej prawdopodobna
zdarzeń
z prawdopodobieństwom
przy
doświadczeniach (wartość
wtedy maksymalna):

• jeśli
  nie jest liczbą całkowitą, to
  równia się całej części tej liczby, tzn.
  ;

• jeśli
  jest liczbą całą, to
  równia się
  i
  .

Przykłady: 20.62-20.66.

Twierdzenie 2.3.2 (rozkład Poissona).

Gdy przy
prawdopodobieństwo
w ten sposób, że
jest stała, to dla każdego
mamy prawo małych liczb

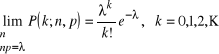
Definicja 2.3.2. Mówimy, że zmienna losowa
ma rozkład Poissona, jeśli przyjmuje ona wartości
każdą z prawdopodobieństwem

.

Zauważmy, że

,

oraz wartość przeciętna

wariancja

.

Interpretacja fizyczna jest oczywista. Zaznaczmy, że praktyce iloczyn
nie przekracza 10.

Przykład 2.3.7. Dwa procenty lamp mają wady. Do jednego pudełka pakuje się 100 sztuk lamp. Jakie prawdopodobieństwo, że
z nich będzie z wadami?

Takie prawdopodobieństwo określa się wzorem

(
)

lub przybliżono

.

W rozważanym przypadku
,
i
. Żeby odpowiedzieć na pytanie po ile sztuk należę pakować do pudełka, aby
pudełek zawierał nie mniej niż 100 sztuk dobrych lamp, należę rozwiązać równanie

,

gdzie
,
— liczba naturalna.

Twierdzenie 2.3.3 (de Moivre'a - Laplace'a). Dla dowolnych liczb rzeczywistych
i
mamy

.

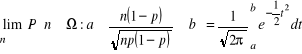
Wzór ten pozwala nam obliczać dla dużych
(rzędu kilkudziesięciu) przybliżone wartości prawdopodobieństwa, ilość sukcesów
będzie zawarta w przedziale

.

Przykład 2.3.8. Teatr ma 1000 miejsc i dwa wejścia, każde z których zaopatrzone w szatnie. Widzowie niezależne z prawdopodobieństwom
wybierają jedno z wejść. Ile wieszaków powinno być w szatnie, aby z prawdopodobieństwom
każdy z 1000 widzów mógł zostawić płacz przy wejściu?

Mamy tu
,
,
,
. Z tablic znajdujemy wartość
taką, żeby

.

Mamy
. Wtedy z twierdzenia de Moivre'a - Laplace'a znajdujemy

,

czyli 527 miejsc.

Definicja 2.3.3. Rozkład geometryczny mamy wtedy, kiedy

,
,

Typowym przykładem tego rozkładu będzie czas oczekiwania
na pierwszy sukces, jeżeli próby powtarzane niezależnie, w jednakowym odstępie czasu i z prawdopodobieństwem
.

Definicja 2.3.4. Rozkład hipergeometryczny mamy wtedy, kiedy

,
,
.

Badana populacja ma
elementów, z których
ma pewną cechę, a
tej cechy niema. Losujemy bez zwracania próbkę
elementową, powyższe daje prawdopodobieństwo znalezienia
z badaną cechą.

Definicja 2.3.5. Rozkład normalny mamy wtedy, kiedy

.

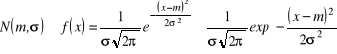
Definicja 2.3.6. Rozkład wykładniczy mamy wtedy, kiedy

gdzie
— stała rzeczywista. Jest, to np. długość życia urządzenia jeśli ona nie zależę od dotychczasowego czasu życia.

Twierdzenie 2.3.4 (wzór Sterlinga). Przy dużych wartościach
wykonuje się wzór przybliżony

.

RACHUNEK PRAWDOPODOBIEŃSTWA