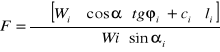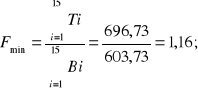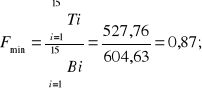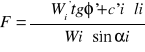Obiektem badanym jest skarpa o nachyleniu 1:1,5. Zadaniem jest określenie jej stateczności.
Schemat obiektu zawierający układ warstw geotechnicznych oraz geometrię skarpy i zadane obciążenie przedstawia rysunek 1.
2. Określenie stopnia złożoności warunków geotechnicznych i kategorii geotechnicznej.
Warstwa pierwsza o miąższości 2 m to piasek gruby o stopniu zagęszczenia
Id = 0,7. Warstwę drugą o miąższości 4 m tworzy glina piaszczysta o wskaźniku konsystencji Ic = 0,7 należąca do grupy konsolidacyjnej C, czyli gruntów spoistych nieskonsolidowanych (ale nie morenowych). Warstwa trzecia to glina Pylata należąca do gupy konsolidacyjnej B. Poziom wód gruntowych ustala się na tej samej wysokości co poziom wody w zbiorniku, czyli na głębokości 2 m.
Na podstawie danych o warunkach gruntowo - wodnych stwierdza się, że warunki geotechniczne są proste.
Na podstawie oceny stopnia złożoności warunków geotechnicznych, oraz zadanego schematu obiektu (skarpa o wysokości 10 m) stwierdza się, że obiekt należy do drugiej kategorii geotechnicznej.
3. Ustalenie wartości obliczeniowych parametrów wydzielonych warstw:
Tabela 1a. Podstawowe cechy fizyczne
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

'
|

sat
|
|
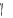
'
|
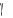
sat
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tabela 1b. Parametry wytrzymałościowe
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dla niespoistych c=0 i 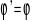
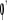
= 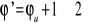
dla gliny piaszczystej (grunt spoisty).
4. Analiza stateczności skarpy dla kołowo-cylindrycznej powierzchni poślizgu metodą Felleniusa.
4.1. Założenia metody Felleniusa
płaski stan odkształcenia
kołowo-cylindryczna powierzchnia poślizgu
jednoczesne przemieszczenie punktów wzdłuż całej powierzchni poślizgu (klin odłamu zachowuje się jak bryła sztywna).
zakłada się brak oddziaływań między elementami (paskami) klina odłamu.
rozpatruje się tylko jeden warunek równowagi - warunek momentu dla całego klina odłamu
4.2. Obliczenie stateczności dla skarpy bez wody.
4.2.1 Wyznaczenie sił Wi w paskach
Gi stanowi składową ciężaru właściwego pochodzącego od każdego rodzaju gruntu w poszczególnych paskach;
Wi - wypadkowa obciążeń (sprowadzona do środka ciężkości bloku);
Ni - reakcja podłoża na składową normalną siły Wi;
Ti - opór tarcia i spójności (siła bierna, utrzymująca);
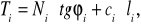
ci,φi - dla gruntu w podstawie bloku;
4.2.2. Obliczanie współczynnika stateczności F.
Wi - ciężar paska z uwzględnieniem obciążenia zewnętrznego
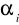
- kąt między powierzchnią poślizgu paska a poziomem (odczytane z rysunku);
li - szerokość powierzchni poślizgu paska (odczytane z rysunku);
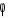
- kąt tarcia wewnętrznego (odczytane z normy);
c -spójność (odczytana z normy);
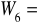
G16+G26+G36=10,66+117,33+47,90=175,89kN
4.3. Obliczanie stateczności dla skarpy z wodą
4.3.1 Wyznaczenie sił Wi w paskach
Stwierdzono, że najniebezpieczniejsza krawędź poślizgu skarpy zlokalizowana jest tak, że zaznaczone obciążenie nie ma wpływu na jej stateczność, toteż nie mogło ono zostać uwzględnione w obliczeniach.
Z dwóch rozpatrywanych przypadków tylko w jednym skarpę można uznać za stosunkowo stabilną, bowiem współczynnik stateczności mieści się w przedziale [1,1;1,3] (za Wiłun Z., Zarys geotechniki, WKŁ, Warszawa, 1976,2001) mimo, iż zaleca się odnosić do wielkości 1,3, od której otrzymany współczynnik jest mniejszy. Zapobiegawczo można zakotwić tę skarpę aby podwyższyć ów współczynnik oraz pewność stateczności skarpy.
Minimalny współczynnik stateczności w drugim przypadku (gdy zbiornik jest wypełniony wodą) jest mniejszy od jedności co wskazuje na niestabilność projektowanej skarpy. Zaleca się w tym wprowadzenie środków podwyższających stateczność skarpy, np zmienieni kąta nachylenia skarpy, lub wprowadzenie kotew umacniających zbocze.
Zestawienie tabelaryczne wartości sił działających na paski przy zalaniu wodą:
Wyznaczenie współczynnika stateczności F w przypadku zbiornika zalanego wodą:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()