Politechnika Śląska

Wydział Mechaniczny Technologiczny

Mechanika i Budowa Maszyn

Grupa 6

Temat ćw.: Wyznaczenie szerokości przerwy energetycznej termistora.

Sekcja 10

Paweł Śliwiak

Roman Zawisz

Krzysztof Szymiczek

1. Wprowadzenie :

Przewodność właściwa półprzewodników określona jest przez koncentrację nośników ruchliwość :

σ=e(n₊₊+n_-_-).

W celu zbadania temperaturowej zależności przewodnictwa elektrycznego pół­przewodników należy przeanalizować zależność temperaturową koncentracji i ruchli­wości obydwu rodzajów nośników: elektronów i dziur.

Stan energetyczny elektronów w sieci krystalicznej półprzewodnika opisany jest elektrodynamiką kwantową. Prawdopodobieństwo obsadzenia stanu ener­getycznego o wartości W określa funkcja rozkładu Fermiego-Diraca:

,

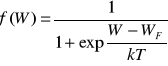
gdzie: k - stała Boltzmanna, T - temperatura, a W_F - tzw. energia Fermiego. Energia odpowiada poziomowi, którego prawdopodobieństwo obsadzenia przez elektron wynosi 1/2. Położenie poziomu Fermiego jest jednoznacznie związane z kon­centracją nośników ładunku w danej temperaturze. Znając rozkład koncentracji stanów dna pasma przewodnictwa W_C:

i odpowiednio w pobliżu wierzchołka pasma podstawowego W_V:

można obliczyć koncentrację nośników w danej temperaturze. W powyższych wzo­rach oznaczono przez m* - masy efektywne elektronów i dziur, a h - stałą Plancka.

Można wykazać, że iloczyn koncentracji nośników zależy tylko od szerokości przerwy energetycznej W_g i temperatury T:

np =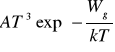
gdzie:

jest wielkością stałą. Ze wzoru wynika bardzo ważny wniosek, że iloczyn kon­centracji nośników ładunku nie zależy od położenia poziomu Fermiego, ani od tego, czy półprzewodnik zawiera domieszki lub defekty sieci, czy też nie. W półprzewodni­ku samoistnym koncentracje elektronów i dziur są sobie równe:

n = p =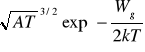

Wstawiając przykładowo dla germanu wartość szerokości przerwy energetycznej W_g = 0,67 eV otrzymamy w temperaturze pokojowej (300 K) koncentrację nośników n =- 2,4 * 10⁹ m^-3, a dla krzemu (W_g = l,11 eV) - n = 1,5 * 10¹⁶ m^-3. Ruchliwość nośników zależy od mechanizmu rozpraszania ich energii. Jeśli Wg » kT, to składnik T^3/2+p zmienia się z tem­peraturą znacznie wolniej niż wielkość eksponencjalna. Można więc przyjąć, że:

Na rys. 2.1 pokazano typowy przebieg temperaturowej zależności przewodności elektrycznej półprzewodnika w skali logarytmiczno-odwrotnościowej
.

Na wykresie tym można wyróżnić trzy charakterystyczne obszary:

I - w zakresie niskich temperatur praktycznie nie zachodzi termiczna generacja par elektron-dziura, a zjo­nizowana jest tylko część domie­szek; koncentracja zjonizowanych domieszek zależy wykładniczo od temperatury

II - w zakresie średnich temperatur (-150°C ÷ +75°C - dla germanu i -100°C ÷ +15O°C - dla krzemu) praktycznie wszystkie domieszki są zjonizowane i prze­wodność praktycznie jest stała, ponieważ w dalszym ciągu nie zachodzi termicz­na generacja par elektron-dziura,

III - w zakresie wysokich temperatur dominuje termiczna generacja par elektron­dziura i przewodność elektryczna półprzewodnika zmienia się z temperaturą tak jak dla półprzewodnika samoistnego.

Zewnętrzne pole elektryczne zmienia energię nośników ładunku powodując w konsekwencji zmianę ruchliwości, przy czym ruchliwość może rosnąć lub zmniej­szać się zależnie od mechanizmu rozpraszania. Silne pole elektryczne prowadzi do zmiany koncentracji nośników ładunku (jonizacja zderzeniowa, zjawisko Zenera, we­wnętrzna emisja polowa, zjawisko Starka).

Termistory są przyrządami półprzewodnikowymi wykorzystującymi zmiany opor­ności przy zmianie temperatury. Zasadniczo termistory posiadają ujemny współczynnik temperaturowy oporności, a ich opór zmienia się z temperaturą zgodnie ze wzorem:

gdzie R_∞ - oporność w temperaturze dążącej do nieskończoności, B = W_g/2k - stała materiałowa. Tak zwana znormalizowana rezystancja termistora R₂₅ definiowana jest jako jego oporność w temperaturze 25°C.

Temperaturowy współczynnik oporności określa względną zmianę oporności przy zmianie temperatury o 1 deg:

Temperaturowy współczynnik oporności określa się zwykle w odniesieniu do tem­peratury 25°C:

Termistor jest elementem nieliniowym, a wykres spadku napięcia na jego końcach jako funkcji natężenia płynącego prądu jest krzywą z wyraźnym maksimum (rys. 2.2). W zakresie niewielkich prądów opór pozostaje stały i obserwuje się prawie liniową za­leżność pomiędzy napięciem i natężeniem prądu (zgodność z prawem Ohma). Przy wzroście prądu termistor zaczyna się nagrzewać, co powoduje zmniejszanie się rezy­stancji. Dalszy wzrost prądu powoduje tak silny spadek rezystancji, że napięcie maleje.

Zwykle termistory wykonuje się w postaci spieku mieszaniny sproszkowanych materiałów półprzewodnikowych (termistorem jest grafit oraz niebieski diament).

Termistory z dodatnim współczynnikiem tempe­raturowym oporności wykonuje się z tytanianu baru BaTi0₃ i jego roztworów stałych, z SrTi0₃ i BaSn0₃ domieszkowanych La, Ce itp. Można stosować rów­nież monokrystaliczny krzem domieszkowany borem. Dobierając odpowiedni skład związków tytanianowych uzyskuje się termistory o współczynniku temperaturowym rzędu 50%/°C. Termistory z dodatkiem cyny posiadają liniową zależność ln R(T) w stosun­kowo szerokim przedziale temperatur. Termistory stosuje się głównie do pomiaru temperatury oraz w układach elektronicznych do kompensacji termicznej.

2. Przebieg ćwiczenia :

1. Łączymy obwód wg schematu pokazanego poniżej.

2. Zmieniając temperaturę kąpieli olejowej w przedziale 20°C ÷ 60°C co 3 deg mie­rzymy oporność termistora.

3. Pomiary powtarzamy podczas ochładzania termistora.

4. Rysujemy wykres zależności temperaturowej R = f(T).

5. Rysujemy wykres zależności
i obliczamy współczynniki regre­sji liniowej tej zależności.

6. Obliczamy szerokość przerwy energetycznej półprzewodnika:

i przeprowadzamy rachunek błędów.

7. Łączymy obwód wg poniższego schematu

8. Zmieniając napięcie zasilania w granicach od zera do 50 V co 2 V notujemy wska­zania mierników.

9. Rysujemy wykres charakterystyki napięciowo-prądowej badanego termistora.

Sprawozdanie z fizyki

- 4 -

---