1. Wprowadzenie teoretyczne:

Ciecz rzeczywista przy przepływie pokonuje opory kosztem energii mechanicznej. Ubytek energii mechanicznej wyraża się stratami ciśnienia między dwoma rozpatrywanymi przekrojami poprzecznymi strumienia.

Straty ciśnienia mogą być :

• nagłe, wywołane przez aparaturę zainstalowana na przewodzie, zmiany kierunku ruchu, zmiany przekroju poprzecznego przewodu ( opory miejscowe)

• stopniowe, proporcjonalne do długości przewodu (opory liniowe).

Piezometryczna linia ciśnień pokazuje wysokość słupa wody wzdłuż rozpatrywanego odcinka przewodu. Po przejściu wody z mniejszej do większej średnicy ciśnienie rośnie, gdyż zmienia się prędkość przepływu (maleje), przy zachowanym wydatku.

2. Opis modelów i metodyka pomiarów:

a) Do wyznaczenia współczynników oporów liniowych λ i miejscowych ζ służy model którego schemat przedstawiony jest poniżej:

Rys.1 Schemat stanowiska do pomiarów współczynników oporów liniowych i miejscowych oraz obserwacji piezometrycznej linii ciśnień.

W ćwiczeniu wykorzystano następujące przewody:

• Przewód plastikowy nr 2 ( D=16mm, L=
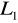
  =7,20m)

• Przewód stalowy czysty nr 5 (D=16mm, L=
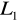
  =7,20m)

• Przewód stalowy skorodowany nr 7 (D=21mm, L=
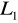
  =7,20m)

• Przewód plastikowy z oporem miejscowym (D=16mm, L=
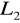
  =2,40m)

Użyto również:

• Manometry cieczowe

• Termometry

Metodyka pomiarów opierała się głównie na zmianie wielkości natężenia przepływu w przewodach, odczytach wysokości cieczy manometrycznej w manometrach oraz natężenia przepływu wody w rotametrze.

b) Do wykonania obserwacji piezometrycznej linii ciśnień posłużył przewód o zmiennych średnicach (nr 4). W dziesięciu przekrojach przewodu podłączone są przewody impulsowe piezometrów (bezpośrednio przed i za oporem miejscowym).

Schemat układu przedstawia następujący rysunek:

Rys.2 Schemat układu do obserwacji piezometrycznej linii ciśnień.

Metodyka pomiarów polegała na odczytywaniu wskazań piezometrów dla różnych warunków przepływu strumienia wody.

3.Wyniki pomiarów:

Przewód plastikowy nr 2 ( D=16mm, L=7,20m):

N	H1		H2		Q		Wartości uśrednione
		Odczyt 1	Odczyt 2	Odczyt 1	Odczyt 2	Odczyt 1	Odczyt 2	H1 [mm]	H2[mm]	Q[l/min]
1	330	330	300	298	46,0	46,0	330,0	299,0	46,00
2	306	307	280	282	44,5	44,5	306,5	281,0	44,50
3	283	287	262	257	42,5	43,0	285,0	259,5	42,75
4	268	271	250	246	41,5	42,0	269,5	248,0	41,75
5	249	244	225	222	39,5	39,5	246,5	223,5	39,50
6	228	231	210	206	38,0	38,5	229,5	208,0	38,25
7	197	199	180	177	35,0	35,0	198,0	178,5	35,00
8	168	170	155	151	32,0	32,0	169,0	153,0	32,00
9	140	142	130	126	29,0	29,0	141,0	128,0	29,00
10	87	88	82	80	22,5	22,5	87,5	81,0	22,50
11	44	45	42	41	15,0	15,5	44,5	41,5	15,25
12	17	18	17	17	9,0	9,0	17,5	17,0	9,000

• Przewód stalowy czysty nr 5 (D=16mm, L=7,20m):

N	H1		H2		Q		Wartości uśrednione
		Odczyt 1	Odczyt 2	Odczyt 1	Odczyt 2	Odczyt 1	Odczyt 2	H1 [mm]	H2[mm]	Q[l/min]
1	425	429	434	430	33,5	33,0	427,0	432,0	33,25
2	412	415	422	418	32,0	31,5	413,5	420,0	31,75
3	386	389	397	393	30,5	31,0	387,5	395,0	30,75
4	353	356	365	361	29,5	30,0	354,5	363,0	29,75
5	322	325	335	332	28,0	28,0	323,5	333,5	28,00
6	300	302	311	308	27,0	27,0	301,0	309,5	27,00
7	266	268	282	280	25,5	26,0	267,0	281,0	25,75
8	230	235	252	250	24,0	24,0	232,5	251,0	24,00
9	180	185	205	202	21,0	21,5	182,5	203,5	21,25
10	108	110	138	137	17,0	17,0	109,0	137,5	17,00
11	76	77	108	107	14,5	15,0	76,5	107,5	14,75
12	26	27	60	59	9,5	10,0	26,5	59,5	9,750

Przewód stalowy skorodowany nr 7 (D=21mm, L=7,20m):

N	H1		H2		Q		Wartości uśrednione
		Odczyt 1	Odczyt 2	Odczyt 1	Odczyt 2	Odczyt 1	Odczyt 2	H1 [mm]	H2[mm]	Q[l/min]
1	142	143	116	116	52,5	53,0	142,5	116	52,75
2	137	138	110	110	51,0	51,5	137,5	110	51,25
3	129	129	100	100	49,5	50,0	129,0	100	49,75
4	119	118	89	89	47,0	47,0	118,5	89	47,00
5	116	116	88	88	46,5	47,0	116,0	88	46,75
6	111	111	83	83	45,0	45,5	111,0	83	45,25
7	99	98	70	70	42,0	42,5	98,5	70	42,25
8	80	80	52	52	37,5	38,0	80,0	52	37,75
9	76	76	47	47	36,0	36,0	76,0	47	36,00
10	54	54	25	25	28,5	29,0	54,0	25	28,75
11	47	47	17	17	25,0	25,5	47,0	17	25,25
12	34	34	5	5	7,5	8,0	34,0	5	7,750

• Przewód z oporem miejscowym (D=16mm, L=2,40m):

N	H1		H2		Q		Wartości uśrednione
		Odczyt 1	Odczyt 2	Odczyt 1	Odczyt 2	Odczyt 1	Odczyt 2	H1 [mm]	H2[mm]	Q[l/min]
1	325	335	320	310	41,0	41,0	330,0	315,0	41,00
2	305	310	300	295	39,5	40,0	307,5	297,5	39,75
3	270	280	280	270	37,5	37,5	275,0	275,0	37,50
4	250	260	270	250	36,0	37,5	255,0	260,0	36,75
5	240	248	257	252	35,5	36,5	244,0	254,5	36,00
6	220	230	240	235	34,0	35,5	225,0	237,5	34,75
7	200	208	222	215	33,5	34,0	204,0	218,5	33,75
8	150	156	175	170	28,5	29,0	153,0	172,5	28,75
9	123	128	155	150	26,0	26,5	125,5	152,5	26,25
10	80	85	120	115	22,0	22,5	82,5	117,5	22,25
11	50	55	90	85	18,5	19,0	52,5	87,5	18,75
12	25	30	70	65	15,0	15,0	27,5	67,5	15,00

Wysokość słupa wody w piezometrach (przewód o różnych średnicach):

N	Q	H1	H2	H3	H4	H5	H6	H7	H8	H9	H10
1	16	125,0	128,5	120,0	122,5	118,5	115,5	107,5	98,0	81,5	63,5
2	18	155,5	160,0	163,5	154,5	150,0	147,0	139,5	126,0	107,0	84,5

Wartości od H1 do H10 są w mm zaś Q w l/min

Temperatura wody w przewodach t_w=2,5^oC

Temperatura otoczenia t=19^oC

Wszelkie pomiary natężenia przepływu zostały wykonane za pomocą rotametru.

4.Obliczenia wielkości hydraulicznych:

Określając wysokość oporów liniowych
wykorzystano wzór:
,gdzie:

ρ_cm - gęstość cieczy manometrycznej (rtęć o gęstości 13548 kg/m³, wartość odczytana z tablic dla temperatury 19^oC),

ρ' - gęstość wody w manometrze (999,965 kg/m³ -założono, ze ρ'=ρ),

ρ - gęstość wody w przewodzie (999,965 kg/m³ dla temperatury 2,5^oC).

Średnia prędkość przepływu w przewodzie obliczona została ze wzoru:




gdzie: D - średnica wewnętrzna przewodu (dla przewodu nr 2 D=16mm=0,016m) Q - wydatek
,[l/min]
różnica wskazań w manometrze [mm],[m]

• Przewód plastikowy nr 2 ( D=16mm, L=7,20m) :

N	Q[m^3/s]	ΔH [m]	hl [m]	v[m/s]
1	0,000767	0,6290	7,89	3,82
2	0,000742	0,5875	7,37	3,69
3	0,000713	0,5445	6,83	3,55
4	0,000696	0,5175	6,49	3,46
5	0,000658	0,4700	5,90	3,28
6	0,000638	0,4375	5,49	3,17
7	0,000583	0,3765	4,72	2,90
8	0,000533	0,3220	4,04	2,65
9	0,000483	0,2690	3,38	2,41
10	0,000375	0,1685	2,11	1,87
11	0,000254	0,0860	1,08	1,26
12	0,000150	0,0345	0,43	0,75

Obliczenia współczynnika oporów liniowych zostały dokonane na podstawie wzoru:


,

gdzie:

L₁ - długość badanego odcinka (L₁=7,20m),

g - przyspieszenie ziemskie (g=9,81 m/s²)

zaś liczba Reynoldsa




gdzie:

ν - kinematyczny współczynnik lepkości płynu (dla wody o temperaturze 2,5^oC wynosi 1,6425 10^-6 m²/s)


- prędkość przepływu wody [m/s]

Przewód plastikowy nr 2 ( D=16mm, L=7,20m):

N	Q[m^3/s]	hl [m]	v[m/s]	λ	Re
1	0,000767	7,89	3,82	0,02364	37163	0,000140	1939
2	0,000742	7,37	3,69	0,02360	35951	0,000146	1878
3	0,000713	6,83	3,55	0,02370	34537	0,000154	1808
4	0,000696	6,49	3,46	0,02362	33730	0,000158	1767
5	0,000658	5,90	3,28	0,02396	31912	0,000172	1676
6	0,000638	5,49	3,17	0,02379	30902	0,000178	1626
7	0,000583	4,72	2,90	0,02445	28276	0,000204	1495
8	0,000533	4,04	2,65	0,02501	25853	0,000233	1373
9	0,000483	3,38	2,41	0,02544	23429	0,000269	1252
10	0,000375	2,11	1,87	0,02647	18178	0,000392	990
11	0,000254	1,08	1,26	0,02941	12320	0,000726	697
12	0,000150	0,43	0,75	0,03388	7271	0,001732	444

Wykres
dla przewodu plastikowego nr 2 ( D=16mm, L=7,20m):




Dla pozostałych przewodów obliczenia zostały dokonane analogicznie.

Przewód stalowy czysty nr 5 (D=16mm, L=7,20m):

N	Q[m^3/s]	ΔH[m]	hl [m]	v[m/s]
1	0,000554	0,8590	10,78	2,76
2	0,000529	0,8335	10,46	2,63
3	0,000513	0,7825	9,82	2,55
4	0,000496	0,7175	9,00	2,47
5	0,000467	0,6570	8,24	2,32
6	0,000450	0,6105	7,66	2,24
7	0,000429	0,5480	6,88	2,14
8	0,000400	0,4835	6,07	1,99
9	0,000354	0,3860	4,84	1,76
10	0,000283	0,2465	3,09	1,41
11	0,000246	0,1840	2,31	1,22
12	0,000163	0,0860	1,08	0,81

N	Q[m^3/s]	hl [m]	v[m/s]	λ	Re
1	0,000554	10,78	2,76	0,06180	26862	0,000442	1424
2	0,000529	10,46	2,63	0,06577	25651	0,000492	1363
3	0,000513	9,82	2,55	0,06583	24843	0,000511	1323
4	0,000496	9,00	2,47	0,06448	24035	0,000522	1283
5	0,000467	8,24	2,32	0,06666	22621	0,000576	1212
6	0,000450	7,66	2,24	0,06661	21813	0,000601	1171
7	0,000429	6,88	2,14	0,06574	20803	0,000629	1121
8	0,000400	6,07	1,99	0,06677	19389	0,000692	1050
9	0,000354	4,84	1,76	0,06799	17168	0,000814	939
10	0,000283	3,09	1,41	0,06785	13734	0,001070	768
11	0,000246	2,31	1,22	0,06727	11916	0,001274	677
12	0,000163	1,08	0,81	0,07196	7877	0,002307	475

Wykres
dla przewodu stalowego czystego nr 5:




Przewód stalowy skorodowany nr 7 (D=21mm, L=7,20m):

N	Q[m^3/s]	ΔH[m]	hl [m]	v[m/s]
1	0,000879	0,2585	3,24	2,54
2	0,000854	0,2475	3,11	2,47
3	0,000829	0,2290	2,87	2,40
4	0,000783	0,2075	2,60	2,26
5	0,000779	0,2040	2,56	2,25
6	0,000754	0,1940	2,43	2,18
7	0,000704	0,1685	2,11	2,03
8	0,000629	0,1320	1,66	1,82
9	0,000600	0,1230	1,54	1,73
10	0,000479	0,0790	0,99	1,38
11	0,000421	0,0640	0,80	1,22
12	0,000129	0,0390	0,49	0,37

N	Q[m^3/s]	hl [m]	v[m/s]	λ	Re			Uwagi
1	0,000879	3,24	2,54	0,02878	32470	0,000056	1685
2	0,000854	3,11	2,47	0,02919	31546	0,000059	1639
3	0,000829	2,87	2,40	0,02866	30623	0,000062	1593
4	0,000783	2,60	2,26	0,02910	28930	0,000068	1508
5	0,000779	2,56	2,25	0,02892	28776	0,000068	1500
6	0,000754	2,43	2,18	0,02935	27853	0,000072	1454
7	0,000704	2,11	2,03	0,02924	26006	0,000080	1362
8	0,000629	1,66	1,82	0,02870	23237	0,000095	1223
9	0,000600	1,54	1,73	0,02940	22159	0,000103	1170
10	0,000479	0,99	1,38	0,02961	17697	0,000149	946
11	0,000421	0,80	1,22	0,03110	15542	0,000188	839
12	0,000129	0,49	0,37	0,20117	4770	0,002652	300	Pomiar odrzucony

Wykres
dla przewodu stalowego skorodowanego nr 7:




Przewód z oporem miejscowym (D=16mm, L=2,40m):

N	Q[m^3/s]	ΔH[m]	hc [m]	v[m/s]
1	0,000683	0,6450	8,09	1,97
2	0,000663	0,6050	7,59	1,91
3	0,000625	0,5500	6,90	1,81
4	0,000613	0,5150	6,46	1,77
5	0,000600	0,4985	6,26	1,73
6	0,000579	0,4625	5,80	1,67
7	0,000563	0,4225	5,30	1,62
8	0,000479	0,3255	4,08	1,38
9	0,000438	0,2780	3,49	1,26
10	0,000371	0,2000	2,51	1,07
11	0,000313	0,1400	1,76	0,90
12	0,000250	0,0950	1,19	0,72

Straty miejscowe zostały obliczone ze wzoru:


λ została wyznaczona z wykresu Colebrooka-White'a (z naniesionymi stratami na długości dla przewodów nr 2, nr 5, nr 7) - strona

N	Q[m^3/s]	hc [m]	v[m/s]	Re	λ	ζ			ζ
1	0,000683	8,09	1,97	33124	0,0238	37,1869	1323	0,0001	0,556
2	0,000663	7,59	1,91	32114	0,0239	37,0865	1285	0,0001	0,570
3	0,000625	6,90	1,81	30296	0,0240	37,9441	1216	0,0001	0,607
4	0,000613	6,46	1,77	29690	0,0241	36,8893	1193	0,0001	0,608
5	0,000600	6,26	1,73	29084	0,0243	37,2122	1170	0,0001	0,623
6	0,000579	5,80	1,67	28074	0,0244	37,0228	1131	0,0001	0,641
7	0,000563	5,30	1,62	27266	0,0248	35,6793	1100	0,0001	0,645
8	0,000479	4,08	1,38	23227	0,0255	38,0046	946	0,0001	0,780
9	0,000438	3,49	1,26	21207	0,0260	38,9544	869	0,0001	0,866
10	0,000371	2,51	1,07	17976	0,0270	38,8620	746	0,0001	1,029
11	0,000313	1,76	0,90	15148	0,0280	38,0994	639	0,0001	1,229
12	0,000250	1,19	0,72	12118	0,0296	40,4087	523	0,0001	1,652

Wykres ζ(Re) dla oporu miejscowego (4 kolana):




Piezometryczna linia ciśnień:




N	Q	H1	H2	H3	H4	H5	H6	H7	H8	H9	H10
1	16	125,0	128,5	120,0	122,5	118,5	115,5	107,5	98,0	81,5	63,5

4.Rachunek błędów:

Do obliczenia błędów:
,
,
została wykorzystana metoda różniczki zupełnej:

-Obliczenie błędu
:

Wzór z którego liczono wartość
:




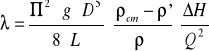
Przyjęto następujące wielkości obarczone błędami odczytu:

Wydatek: ∆Q=0,1 l/min=
m³/s

Wskazanie manometru: ∆h=1 mm=0,001 m







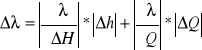
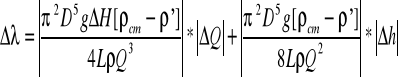
Przykład obliczeniowy dla przewodu plastikowego nr 2:







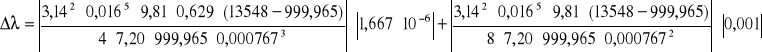
Kolejne obliczenia zostały wykonane analogicznie.

-Obliczeni błędu
:

Wzór z którego liczono liczbę Re:

Re=


Przyjęto następujące wielkości obarczone błędami odczytu:

Wydatek: ∆Q=0,1 l/min=
m³/s

Kinematyczny współczynnik lepkości:
(z uwagi na błąd odczytu temperatury)







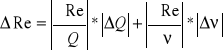
Przykład obliczeniowy dla przewodu plastikowego nr 2:







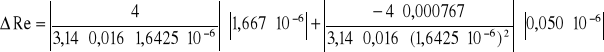
Kolejne obliczenia zostały wykonane analogicznie.

-Obliczeni błędu
:

Wzór z którego liczono wartość
:







Przyjęto następujące wielkości obarczone błędami odczytu:

Prędkość przepływu wody:

(z uwagi na błąd odczytu wydatku jaki przyjęto: ∆Q=0,1 l/min=
m³/s)

Wskazanie manometru: ∆h=1 mm=0,001 m


=0,0001 (stały błąd, gdyż podczas liczenia wartości
,
odczytywano z monogramu Colebrooka-White'a)







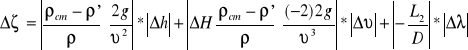
Przykład obliczeniowy dla przewodu z oporem miejscowym:





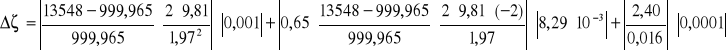
Kolejne obliczenia zostały wykonane analogicznie.

4.Analiza otrzymanych wyników:

• W badanym zakresie wraz ze wzrostem przepływu Q współczynnik strat na długości jak i współczynnik strat miejscowych maleją.

• Najmniejszy współczynnik strat na długości charakteryzuje przewód plastikowy zaś największy przewód stalowy czysty.

• Przepływ cieczy w przewodach pod ciśnieniem charakteryzuje duża wartość liczby Reynoldsa

• Linia ciśnień pokazuje wysokość słupa wody wzdłuż rozpatrywanego odcinka przewodu. Wraz ze wzrostem odległości ciśnienie maleje.

5.Porównanie obliczanej wartości ζ z wartościami literaturowymi:

Średnia wartość ζ w naszych obliczeniach wyniosła : 37,7 (dla 4 plastikowych kolan).

Wartość ζ odczytana z tablic dla jednego kolana wynosi 0,5 ( jednakże spotkano się

też z wartościami 2,0 a nawet 4,0).

Uzyskana wartość ζ jest dużo większa od wartości znalezionych w tablicach.

6.Wnioski:

• Przepływ wody w przewodach odbywa się ruchem burzliwym.

• Przewody stalowe, w porównaniu z przewodami z tworzyw sztucznych, korodują dlatego podczas przepływu cieczy występują tam większe straty energii.

• Współczynnik strat miejscowych zależy od rodzaju przeszkody. W przypadku kolana zależy od: materiału z jakiego jest wykonany (chropowatość), promienia krzywizny, kąta zmiany kierunku oraz wymiarów.

• Właściwości fizyczne cieczy ( w szczególności lepkość) mają duży wpływ na zdolność cieczy do pokonywania oporów.

• Po przejściu wody z mniejszej do większej średnicy ciśnienie rośnie, gdyż zmienia się prędkość (maleje) przepływu, przy zachowanym wydatku.

• Aby doprowadzić ciecz rzeczywistą, w przewodzie zamkniętym, z jednego punktu do drugiego musimy dostarczyć odpowiednią ilość energii, która wystarczy na pokonanie oporów miejscowych i liniowych.

13 z 14

---