1. WEKTOR NAPRĘŻENIA
średnia gęstość sił wewnętrznych na powierzchni F
naprężenie w punkcie A : funkcja wektorowa
2. STAN NAPRĘŻENIA W PUNKCIE
zbiór wektorów naprężenia w ustalonym punkcie przy dowolnej płaszczyźnie przekroju
wybieramy 3 szczególne płaszczyzny przekroju - prostopadłe do osi układu współrzędnych
wektor naprężenia przynależny płaszczyźnie prostopadłej do osi x i
wersory normalne płaszczyzn prostopadłych do osi x i
funkcja skalarna 3 skalarów
macierz naprężenia
σ11, σ22, σ33 - naprężenia normalne, pozostałe to napr. styczne
3. KONWENCJA ZNAKOWANIA NAPRĘŻEŃ
napręż. normalne jest dodatnie, jeżeli jest zgodnie skierowane z normalną zewnętrzną płaszczyzny
napr. styczne jest dodatnie, jeżeli:
1) normalna zewnętrzna płaszczyzny jest zgodnie skierowana z osią układu, do której jest ona równoległa
2) naprężenie styczne jest zgodnie skierowane z osią układu, do której jest ono równoległe,
lub gdy oba warunki są jednocześnie niespełnione.
4. TENSOR NAPRĘŻENIA
cos kąta między ściankami = cos kąta między normalnymi do ścianek
siły działające na ściankach Fi
siła działająca na ściance F
warunek równowagi sił (zamknięty przestrzenny wielobok sił)
![]()
symetria macierzy naprężeń ij = ji
itd..........
konwencja sumacyjna
współrzędne wektora naprężenia na ściance o normalnej ![]()
W wyniku pomnożenia wektora przez macierz otrzymujemy wektor, a zatem macierz naprężenia musi być tensorem.
5. TRANSFORMACJA TENSORA NAPRĘŻENIA
macierz przejścia
I wiersz
I kolumna
wiersze macierzy przejścia to współrzędne wersorów nowego układu wyrażone w ukł. starym
kolumny macierzy przejścia to współrzędne wersorów starego układu wyrażone w ukł. nowym
macierz ortonormalna wzg. wierszy i kolumn, tzn.
prawo transformacji
6. NAPRĘŻENIA GŁÓWNE
Poszukujemy takiej płaszczyzny przechodzącej przez dany punkt, aby odpowiadający jej wektor naprężenia ![]()
miał taki sam kierunek jak wersor normalny płaszczyzny ![]()
.
σ - miara wektora
Zauważmy, że utożsamiając kierunek wersora normalnego płaszczyzny z kierunkiem np. "1" osi nowego układu, wektor naprężenia tworzący pierwszy wiersz 'nowego" tensora naprężenia miałby niezerową tylko pierwszą składową - składową normalną. Byłaby ona największa spośród wszystkich możliwych. Takie naprężenie normalne nosi nazwę naprężenia głównego, a odpowiadająca mu płaszczyzna to płaszczyzna główna.
warunek kolinearności
wektor naprężenia
zagadnienie własne
(war. jednostkowej dług. wersora)
Warunek konieczny istnienia rozwiązania ze wzg. na elementy macierzy przejścia
(równ. charakterystyczne)
, ,
równanie charakterystyczne ma zawsze 3 pierwiastki rzeczywiste, które można uporządkować 1 > 2 > 3
każdej z wartości głównych odpowiada płaszczyzna główna, określona wersorem normalnym
wersory określające płaszczyzny główne są ortonormalne, tzn.
dla dowolnego tensora naprężenia zawsze istnieją 3 wzajemnie prostopadłe naprężenia i kierunki (płaszczyzny) główne.
procedura określania kierunków głównych, czyli zarazem macierzy przejścia do kierunków głównych
np. dla = 1
+ (*)
1) wziąć którekolwiek 2 spośród 3 równań, kładąc w nich np. 13 = t
2) znaleźć 11 = 11(t) , 12 = 12(t)
3) wyznaczyć parametr t z warunku " (*) "
4) obliczyć wartości 11 , 12 , 13
5) postąpić analogicznie dla 2
6) wyznaczyć
7. PŁASKI STAN NAPRĘŻENIA
stan naprężenia, dla którego wszystkie składowe leżą w jednej płaszczyźnie, np. (x1, x2).
tensor naprężenia
macierz przejścia
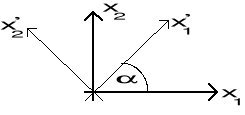
naprężenia główne + przekształcenia
pseudopłaski stan naprężenia - jak wyżej, ale 33 0. Rezultaty jak dla PSN, a trzecie naprężenie główne 3 = 33
8. EKSTREMALNE NAPRĘŻENIA STYCZNE
Problem : W punkcie A znany jest tensor naprężenia w osiach głównych. Jaką płaszczyzną należy przekroić ciało w pkt. A, aby miara rzutu wektora naprężenia odpowiadającego tej płaszczyźnie na nią samą była maksymalna?
wektor naprężenia
wersor normalny
σν - miara rzutu wektora naprężenia na normalną
τν - miara rzutu wektora naprężenia na płaszczyznę
Procedura rozwiązania (1)
(2)
+ warunek (3)
Zadanie sprowadza się do znalezienia ekstremum funkcji (2) z warunkiem pobocznym (3)
1) z war. (3) wyeliminować np. i wstawić do funkcji (2)
2) warunki konieczne istnienia ekstremum + przekształcenia
Rozwiązanie : Naprężenia styczne osiągają swoje ekstrema na płaszczyznach nachylonych pod kątami 45° do płaszczyzn głównych.
;
9. KOŁA MOHRA
Problem : W punkcie A znany jest tensor naprężenia w osiach głównych. Określić zbiór rozwiązań (ν, ν) dla dowolnych płaszczyzn przekroju ciała, przechodzących przez pkt. A.
wektor naprężenia
wersor normalny
σν - miara rzutu wektora na
τν - miara rzutu wektora na płaszczyznę
tensor naprężenia
Procedura rozwiązania
(1)
(2)
+ warunek (3)
Rozwiązanie układu równań (1), (2), (3) wzgl. ma postać :
Z relacji większościowych między naprężeniami głównymi wynikają nierówności:
; ;
Przekształcenia tych nierówności prowadzą do związków:
K23
zewnętrze okręgu o promieniu (2 - 3) / 2 i środku [ (2 + 3) / 2 ; 0 ]
K13
wnętrze okręgu o promieniu (1 - 3) / 2 i środku [ (1 + 3) / 2 ; 0 ]
K12
wnętrze okręgu o promieniu (1 - 2) / 2 i środku [ (1 + 2) / 2 ; 0 ]
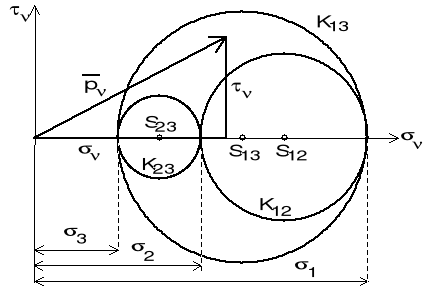
Zastosowanie kół Mohra dla płaskiego stanu naprężenia ( 3 = 0 )
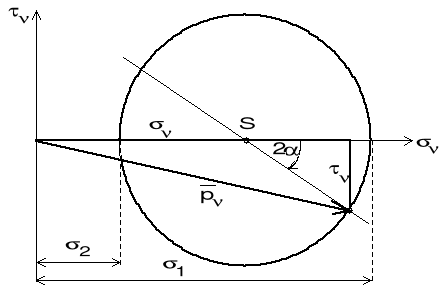
ZADANIE 1 : Dane są naprężenia główne 1 i 2 oraz kąt , pod jakim nachylona jest płaszczyzna do kierunku naprężenia 1. Wyznaczyć naprężenia normalne i styczne przynależne tej płaszczyźnie.
ZADANIE 2: Dany jest tensor naprężenia w pkt. A w dowolnym ukł. współrzędnych (x1, x2). Znaleźć naprężenia główne 1 i 2 oraz ich kierunki.
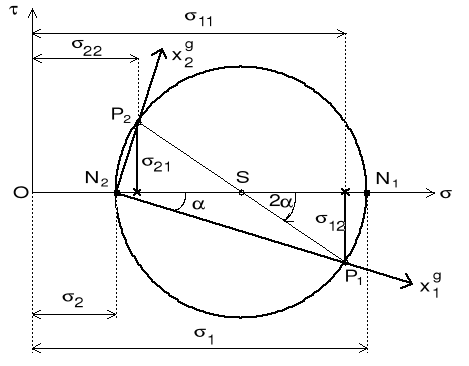
Kolejność czynności:
1) odłożyć na osi "" wartości 11 i 22
2) z punktu = 11 odłożyć na osi "" wartość 12 - jeżeli 12 > 0 to po dodatniej stronie osi "" ( na rysunku przyjęto 12 < 0 ). Z punktu = 22 odłożyć wartość 12 po stronie przeciwnej osi "" . Otrzymujemy punkty P1 i P2
3) połączyć punkty P1 i P2 - punkt S, przecięcia odc. P1-P2 z osią "" jest środkiem koła
4) narysować koło o środku w pkt. S i promieniu S P1 (S P2). Otrzymujemy punkty N1 i N2, przecięcia się okręgu z osią "". Odcinki ON1 i O N2 wyznaczają wartości naprężeń głównych 1 i 2
5) połączyć punkt P1 z N2 - otrzymujemy oś x1gł , określającą kierunek główny odpowiadający pierwszemu naprężeniu głównemu
6) połączyć punkt P2 z N2 - otrzymujemy oś x2gł , określającą kierunek główny odpowiadający drugiemu naprężeniu głównemu.
TEORIA STANU NAPRĘŻENIA 7
, - wektory sił wewnętrznych w punktach powierzchni ΔF wokół punktu A
- suma sił wewnętrznych na powierzchni ΔF
x1
x2
x3
A
x1
x2
x3
A
C
B
E
σ11
σ22
σ12
σ21
σ13
σ23
σ32
σ31
σ33
D
G
F
x1
x2
x3
A
x'2
x'1
x'3
x2
x1
x3
e'1
e'2
e'3
e2
e1
e3
x1
x2
x3
O
x1
x2
σ11
σ22
σ12
σ22
σ21
σ12
σ11
σ21
1
2
3
A
1
2
3
1
2
3
A
WNIOSEK :
Dla danego tensora naprężenia w pkt. A , określonego w osiach głównych, koniec wektora naprężenia odpowiadają-cego dowolnej płaszczyźnie przechodzą-cej przez pkt. A musi leżeć w obszarze określonym przez koła Mohra (obszar "zaciemniony"). Jest to obszar, w którym leżą wszystkie pary ( , )
Wyszukiwarka
Podobne podstrony:
rozcuzu2, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
rfizyczn, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
GEOMPRZE, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
nr wykl, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
bnsp kom, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
mimorozc, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
rozcuzup, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
Mechpek2, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
podstaw1, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
mimroz e, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
belki, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
Mechpek6, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
stodkszt, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, wytrzymalosc
PKM, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, od majka, SPRAWOZDA
2.3, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, laborki-mojeókrzste
Str.4 - Karta technologicza zbiorcza, Politechnika Lubelska, Studia, Studia, organizacja produkcji,
TM10, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, Wydział Mechaniczn
więcej podobnych podstron