Badanie właściwości magnetycznych ciał stałych
Wydział |
Dzień/godz. Poniedziałek 8:15 - 11:00 |
Nr zespołu: |
|||
Inżynierii Lądowej |
Data 8.12.2008 |
1 |
|||
Imię i Nazwisko |
Ocena z przygotowania: |
Ocena ze sprawozdania: |
Ocena: |
||
|
|
|
|
||
|
|
|
|
||
Prowadzący: |
Podpis |
||||
|
Prowadzącego |
||||
|
|
|
|
|
|
|
|
|
|
|
|
Cel ćwiczenia
Ćwiczenie ma na celu określenie magnetycznych właściwości ferromagnetyka w zależności od temperatury i wyznaczenie temperatury Curie.
Wstęp teoretyczny
Ferromagnetyk jest to substancja o silnych własnościach magnetycznych. Każdy atom ferromagnetyka wytwarza własne pole magnetyczne. Atomy te mają ponadto tendencję do ustawiania się w ten sposób, aby ich pole magnetyczne miało ten sam kierunek, co pole magnetyczne atomów sąsiednich. W efekcie tworzą się makroskopowe przestrzenie (o wymiarach liniowych rzędu 10-5 - 10-4 m), w których pole magnetyczne ma stały kierunek. Obszary te nazywa się domenami magnetycznymi. Jako że pole magnetyczne każdej z domen może być ustawione w zupełnie dowolnym kierunku ferromagnetyk może nie wytwarzać zewnętrznego pola magnetycznego. Gdy umieścimy ferromagnetyk w zewnętrznym polu magnetycznym domeny zaczynają ustawiać się zgodnie z kierunkiem zewnętrznego pola magnetycznego. Ferromagnetykami są na przykład: kobalt, żelazo, kobalt, nikiel. Namagnesowany ferromagnetyk wytwarza własne pole magnetyczne. Jego namagnesowanie nazywamy namagnesowaniem trwałym. Ferromagnetyk można rozmagnesować umieszczając go w zewnętrznym polu magnetycznym skierowanym przeciwnie do kierunku pola ferromagnetyka o odpowiedniej wartości (koercja) lub podwyższając temperaturę.
Ze wzrostem temperatury zwiększa się ruch atomów. Gdy temperatura osiąga pewną wartość zwaną temperaturą Curie, wówczas siły utrzymujące uporządkowanie atomów w domenach są zbyt małe, aby domeny mogły dalej istnieć. Następuje rozpad domen magnetycznych a pola magnetyczne poszczególnych atomów są skierowane chaotycznie w różnych kierunkach. Ferromagnetyki tracą swoje właściwości i zachowują się jak zwykłe paramagnetyki.
Właściwości magnetyczne substancji wynikają z ich budowy wewnętrznej. Elektrony krążące wokół jąder atomowych mają orbitalny i spinowy moment magnetyczny. Zjawisko namagnesowania substancji charakteryzuje wektor namagnesowania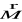 
, który jest stosunkiem momentu magnetycznego występującego w małej objętości substancji do wielkości tej objętości.
Wektor namagnesowania określa wzór:
Wykonanie pomiaru napięcia U pozwala na pośredni pomiar namagnesowania M.
Wartość namagnesowania próbki M jest proporcjonalna do mierzonego napięcia.
Zależność między napięciem w cewce wtórnej, a namagnesowaniem wyraża wzór:
Widzimy więc, że skoro
to
Us ~ ωSZμ0(Hs+Ms)
Do cewki pierwotnej przykładane jest zmienne napięcie. Wytwarzane przez cewkę pierwotną zmienne pole magnetyczne magnesuje próbkę ferromagnetyka. W cewce wtórnej indukuje się napięcie. Pomiar napięcia pozwala na pośredni pomiar magnetyzacji. Wraz ze wzrostem temperatury maleje wielkość magnetyzacji spontanicznej w domenach, maleje więc również wartość magnetyzacji próbki i mierzone napięcie. W okolicach temperatury Curie, gdzie znika uporządkowanie ferromagnetyczne, spadek napięcia jest szczególnie gwałtowny.
Podatność magnetyczną paramagnetyków w zależności od temperatury określa prawo Curie-Weissa:
gdzie:
Wykreślając wykres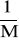 
w funkcji temperatury T możemy określić stałą C jako tangens nachylenia prostej oraz temperaturę Curie jako miejsce zerowe (przecięcie prostej z osią temperatury).
Jako że M~U temperaturę Curie w analogiczny sposób można wyznaczyć wykreślając wykres zależności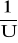 
od T.
Wyniki pomiaru
T[C] ± dT[C] |
U[mV] ± dU[mV] |
1/U[1/mV] |
d(1/U) [1/mV] |
|
|
|
|
24 ± 5 |
660 ± 15 |
0,00152 |
0,00002 |
30 ± 5 |
664 ± 15 |
0,00151 |
0,00002 |
35 ± 5 |
664 ± 15 |
0,00151 |
0,00002 |
40 ± 5 |
667 ± 15 |
0,00150 |
0,00002 |
45 ± 5 |
668 ± 15 |
0,00150 |
0,00002 |
50 ± 5 |
667 ± 15 |
0,00150 |
0,00002 |
55 ± 5 |
666 ± 15 |
0,00150 |
0,00002 |
60 ± 5 |
667 ± 15 |
0,00150 |
0,00002 |
65 ± 5 |
666 ± 15 |
0,00150 |
0,00002 |
70 ± 5 |
666 ± 15 |
0,00150 |
0,00002 |
75 ± 5 |
667 ± 15 |
0,00150 |
0,00002 |
80 ± 5 |
667 ± 15 |
0,00150 |
0,00002 |
85 ± 5 |
667 ± 15 |
0,00150 |
0,00002 |
90 ± 5 |
667 ± 15 |
0,00150 |
0,00002 |
95 ± 5 |
667 ± 15 |
0,00150 |
0,00002 |
100 ± 5 |
667 ± 15 |
0,00150 |
0,00002 |
105 ± 6 |
668 ± 15 |
0,00150 |
0,00002 |
110 ± 6 |
667 ± 15 |
0,00150 |
0,00002 |
115 ± 6 |
666 ± 15 |
0,00150 |
0,00002 |
120 ± 6 |
666 ± 15 |
0,00150 |
0,00002 |
125 ± 6 |
664 ± 15 |
0,00151 |
0,00002 |
130 ± 6 |
666 ± 15 |
0,00150 |
0,00002 |
135 ± 6 |
663 ± 15 |
0,00151 |
0,00002 |
140 ± 6 |
663 ± 15 |
0,00151 |
0,00002 |
145 ± 6 |
661 ± 15 |
0,00151 |
0,00002 |
150 ± 6 |
658 ± 15 |
0,00152 |
0,00002 |
155 ± 6 |
656 ± 15 |
0,00152 |
0,00002 |
160 ± 6 |
651 ± 15 |
0,00154 |
0,00002 |
165 ± 6 |
639 ± 14 |
0,00156 |
0,00002 |
170 ± 6 |
629 ± 14 |
0,00159 |
0,00002 |
175 ± 6 |
613 ± 14 |
0,00163 |
0,00002 |
180 ± 6 |
570 ± 14 |
0,00175 |
0,00003 |
185 ± 6 |
500 ± 13 |
0,00200 |
0,00003 |
188 ± 6 |
460 ± 12 |
0,00217 |
0,00003 |
190 ± 6 |
400 ± 11 |
0,00250 |
0,00004 |
191 ± 6 |
350 ± 10 |
0,00286 |
0,00004 |
192 ± 6 |
320 ± 10 |
0,00313 |
0,00005 |
193 ± 6 |
240 ± 9 |
0,00417 |
0,00006 |
195 ± 6 |
200 ± 8 |
0,00500 |
0,00008 |
196 ± 6 |
180 ± 8 |
0,00556 |
0,00008 |
197 ± 6 |
156 ± 7 |
0,00641 |
0,00010 |
198 ± 6 |
130 ± 7 |
0,00769 |
0,00012 |
199 ± 6 |
110 ± 7 |
0,00909 |
0,00014 |
200 ± 6 |
85 ± 6 |
0,01176 |
0,00018 |
201 ± 6 |
77 ± 6 |
0,01299 |
0,00020 |
202 ± 6 |
73 ± 6 |
0,01370 |
0,00021 |
203 ± 6 |
67 ± 6 |
0,01493 |
0,00022 |
204 ± 6 |
56 ± 6 |
0,01786 |
0,00027 |
205 ± 6 |
50 ± 6 |
0,02000 |
0,00030 |
207 ± 6 |
47 ± 6 |
0,02128 |
0,00032 |
208 ± 6 |
44 ± 6 |
0,02273 |
0,00034 |
209 ± 6 |
42 ± 6 |
0,02381 |
0,00036 |
210 ± 6 |
40 ± 6 |
0,02500 |
0,00038 |
211 ± 6 |
39 ± 6 |
0,02564 |
0,00039 |
212 ± 6 |
38 ± 6 |
0,02632 |
0,00040 |
213 ± 6 |
37 ± 6 |
0,02703 |
0,00041 |
214 ± 6 |
37 ± 6 |
0,02703 |
0,00041 |
215 ± 6 |
36 ± 6 |
0,02778 |
0,00042 |
216 ± 6 |
36 ± 6 |
0,02778 |
0,00042 |
217 ± 6 |
35 ± 6 |
0,02857 |
0,00043 |
218 ± 6 |
35 ± 6 |
0,02857 |
0,00043 |
219 ± 6 |
35 ± 6 |
0,02857 |
0,00043 |
220 ± 6 |
35 ± 6 |
0,02857 |
0,00043 |
IV. Opracowanie wyników
Na podstawie danych zamieszczonych w tabeli sporządzono wykres zależności napięcia U od temperatury T.
Na wykresie zauważamy gwałtowny spadek napięcia próbki. Dla dokładniejszego wyznaczenia szukanej temperatury należy znaleźć punkt przegięcia danej funkcji.
Graficzne oszacowanie temperatury Curie:
Θ = 203 ± 6 [OC]
Sporządzono również wykres zależności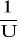 
od T dla temperatur powyżej temperatury Curie.
V .Wnioski
Temperatura Curie wyznaczona z zależności napięcia U od temperatury T wynosiła Θ = 203 ± 6 [OC].
Temperatura Curie
gdzie:
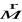
- moment magnetyczny
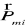
- moment magnetyczny i-tego elektronu lub molekuły
n - liczba atomów w objętości 
V
V - objętość
gdzie:
Z - liczba zwojów cewki wtórnej
S - pole przekroju cewki wtórnej
B - średnia indukcja pola
Hs - średnie natężenie pola
Ms - średnia magnetyzacja próbki
μ0 - przenikalność magnetyczna próżni
gdzie:
C - stała Curie
T - temperatura
Θ -paramagnetyczna temperatura Curie
Stałe C i Θ są charakterystyczne dla danej substancji
antyferromagnetyk
paramagnetyk
ferromagnetyk
Temperatura T
Θ
- Θ