PKM II prow. dr inż. Paweł Pyrzanowski egzamin 27.06.2005 zadania

Zadanie 1:

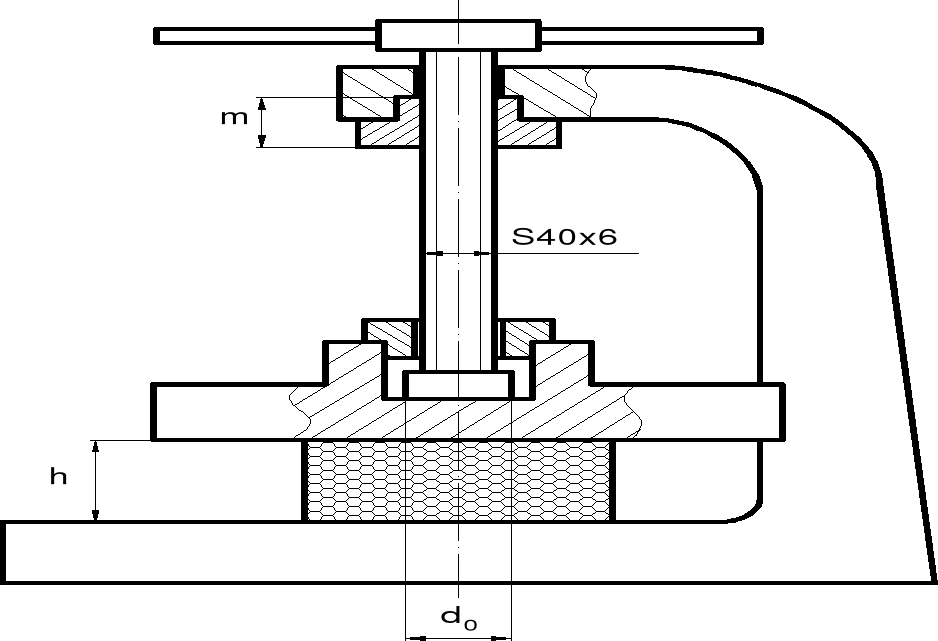
Prasa śrubowa pokazana na rysunku ściska obiekt o wysokości h = 0.1 m i podatności
c = 2·10^-8 m/N. Wyznaczyć:

1. 
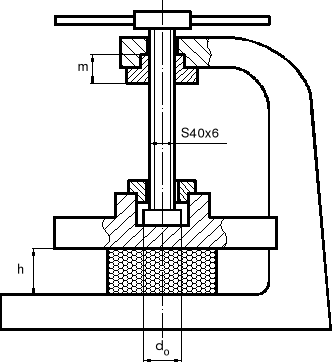
   Moment M_s niezbędny do wywołania
   w obiekcie odkształcenia ε = 5·10^-3. Wartości współczynników tarcia na wszystkich kontak-tujących się powierzchniach przyjąć μ = 0,15. Średnica stopy śruby d₀ = 50 mm.

2. Rozkład siły osiowej i momentu skręcającego
   w śrubie (wykres z wartościami).

3. Minimalną wysokość nakrętki m, jeżeli maksy-malne dopuszczalne naciski na zwojach gwintu wynoszą p_max = 12 MPa.

4. Naprężenia w śrubie w przekroju poniżej nakrętki .

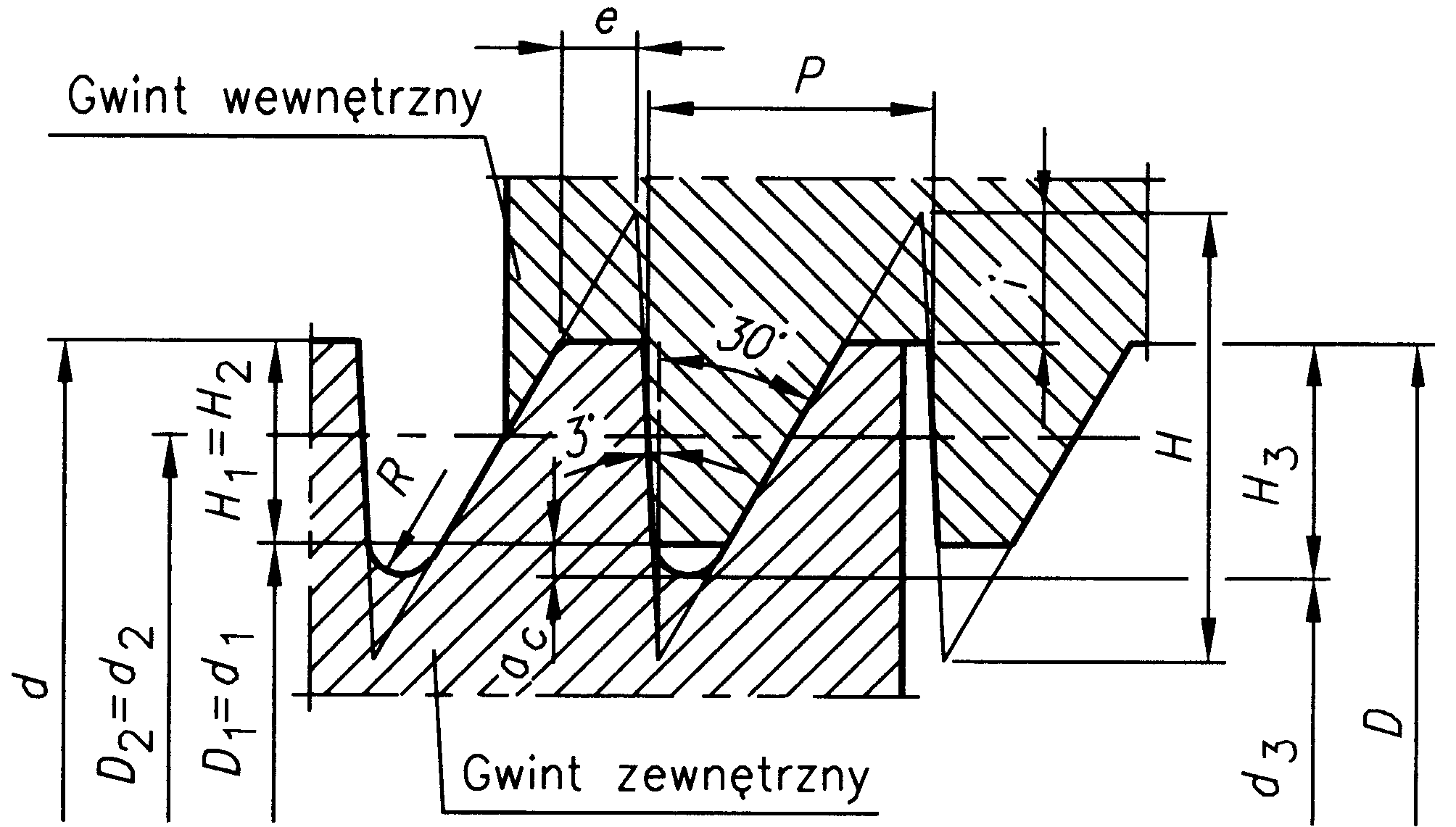
H=1,587911·P; H₁=0,75 ·P; H₃=H₁+a_c;

a_c=0,117767 ·P; d=D; d₂=d-0,75 ·P;

d₃=d-2 ·H₃; D₁=d-1,5·P

PKM II prow. dr inż. Paweł Pyrzanowski egzamin 27.06.2005 zadania

Zadanie 2:

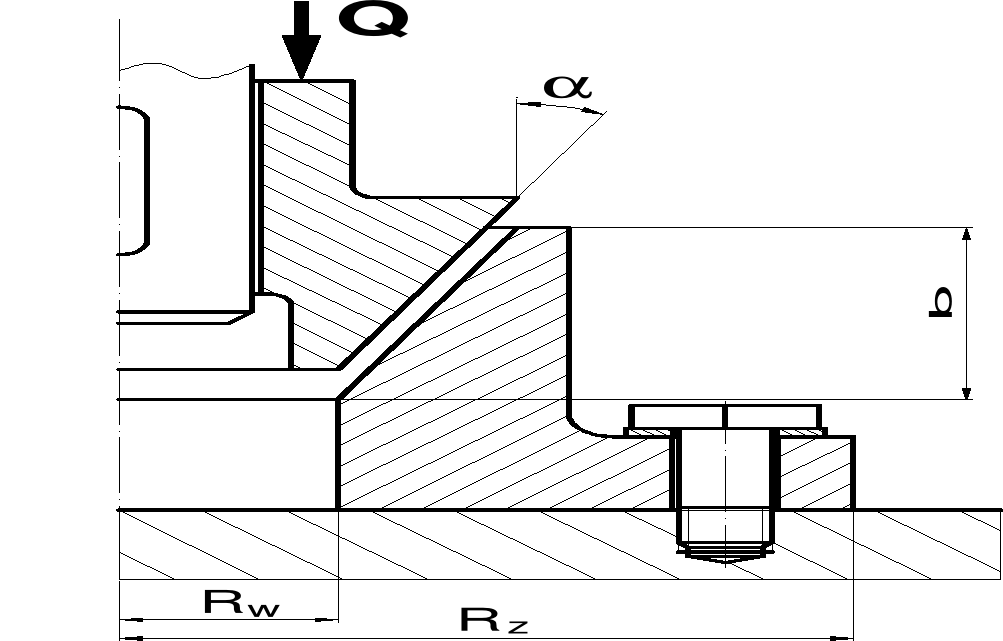
Przedstawiony na rysunku hamulec cierny przeznaczony jest do hamowania wału. Obliczyć:

1. 
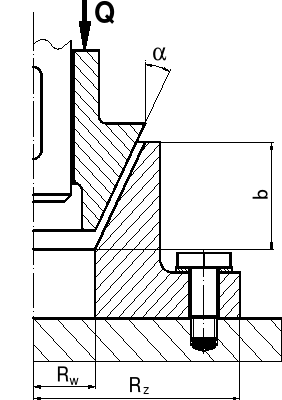
   Maksymalny moment hamowania M, jeżeli przyrost temperatury sprzęgła nie może przekroczyć ΔT = 250ºC. Założyć, że podczas trwającego t = 10 s hamowania wał zmienia prędkośc obrotową liniowo od n = 3000 obr/min do zera, ciepło właściwe elementów grzanych wynosi c = 0,55 kJ/(kg·ºC) a ich masa m = 10 kg.

2. Siłę Q potrzebną do dociskania górnej części sprzęgła do dolnej, jeżeli wewnętrzny promień okładzin R_w = 100 mm, kąt nachylenia stożka  = 15º, długość okładzin mierzona wzdłuż osi sprzęgła b = 80 mm, zaś współczynnik tarcia pomiędzy okładzinami μ = 0,35.

3. Minimalną siłę naciągu F każdej z k = 6 śrub mocujących sprzęgło do podłoża i uniemożliwiających jego obrót w momencie hamowania. Przyjąć współczynnik tarcia pomiędzy podstawą sprzęgła
   a podłożem μ_p = 0,2, promień zewnętrzny podstawy R_z = 180 mm, oraz nieodkształcalność wszystkich części.

PKM II prow. dr inż. Paweł Pyrzanowski egzamin 27.06.2005 zadania

Zadanie 3:

Łożysko kulkowe typu 6007 o nośności statycznej C₀ = 10 200 N i dynamicznej C = 15 900 N obciążone jest stała siłą poprzeczną T = 5000 N oraz stałą siłą osiową N = 2500 N. Obliczyć maksymalną prędkość obrotową wału, jeżeli wymagane jest P = 85 procentowe prawdopodobieństwo bezawaryjnej pracy łożyska w czasie L_s = 3000 h.

---