Akademia Techniczno- Humanistyczna

w Bielsku - Białej

Wydział Nauk o Materiałach i Środowisku

Kierunek: Ochrona Środowiska

Semestr II

Ćwiczenie nr 61

Temat: Wyznaczanie natężenia pola elektrycznego metodą sondy płomykowej

Wykonali:

I Wstęp teoretyczny

Sonda płomykowa

Sonda płomykowa jest bardzo cienką rurką, przez którą przepływa gaz świetlny. Jest ona umieszczona między okładkami kondensatora płaskiego, jej koniec znajduje się na osi symetrii płytek. Sonda umieszczona jest na izolowanym statywie który można przesuwać wzdłuż osi kondensatora. Odległość płytek kondensatora można zmieniać. Potencjał mierzymy woltomierzem elektrostatycznym. Całość podłączona jest do elektrycznego zasilacza wysokonapięciowego.

Kondensator powietrzny

Składa się z dwóch zespołów równoległych płytek(rotor oraz sator), na których zgromadzone są ładunki elektryczne. Pomiędzy płytkami wytworzone jest jednorodne pole elektryczne. Linie sił tego pola są równoległe. Oznacza to, że wartość natężenia pola elektrycznego jest stała a potencjał zmienia się liniowo razem z odległością.

Natężenie i potencjał pola elektrycznego

Pole elektryczne istnieje w przestrzeni otaczającej ciała naelektryzowane i przejawia się w postaci sił działających na ładunki elektryczne. W dowolnym układzie ładunków, każdy ładunek wytwarza własne pole elektryczne. W wyniku nałożenia się tych pól, powstaje pewne pole wypadkowe, które powoduje, że na każdy ładunek w rozważanym układzie działa określona siła.

W celu ilościowego opisania pola elektrycznego wprowadza się wielkość wektorową zwaną natężeniem pola elektrycznego E określoną wzorem:

gdzie:

E - natężenie pola elektrycznego

F - siła działająca w polu na ten ładunek

q₀ - ładunek próbny o bardzo małym dodatnim ładunku punktowym

Ładunek q₀ musi mieć małą wartość by jego własne pole nie zakłóciło badanego natężenia pola.

Natężenie pola może elektrycznego może mieć różną wartość i kierunek w różnych punktach pola - wówczas E jest funkcją położenia: E = E(x, y, z). Szczególnym zaś przypadkiem pola elektrycznego jest pole jednorodne, w którym wektor natężenia pola ma wszędzie jednakową wartość i ten sam kierunek, czyli spełnia warunek E = const. W polu elektrostatycznym natężenie pola nie zmienia się w czasie, co można zapisać w postaci warunku:

Pole elektrostatyczne w danym punkcie przestrzeni można scharakteryzować podając jego potencjał elektryczny. Jest to wartość skalarna, która określa stosunek energii potencjalnej dodatniego ładunku próbnego w danym punkcie pola do wielkości tego ładunku.

Potencjał pola możemy zapisać w następujący sposób:

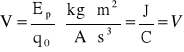
gdzie:

V - potencjał elektryczny pola

E_p - Energia potencjalna w danym punkcie pola

q₀ - ładunek próbny o bardzo małym dodatnim ładunku punktowym

Przyjmuje się, że energia potencjalna ładunku nieskończenie odległego od źródła pola elektrycznego jest równe zero. Zatem potencjał elektryczny danego punktu pola jest równy liczbowo pracy na jednostkę ładunku wykonywanej przez siły pola przy przenoszeniu jednostkowego ładunku dodatniego z danego punktu do punktu nieskończenie odległego.

Różnicę potencjałów ΔV między dwoma punktami pola elektrycznego określamy jako napięcie elektryczne U i można zapisać w postaci wzoru:

U = ΔV = (V₁-V₂) [V]

Związek między wartością natężenia pola E i potencjałem V.

Pomiędzy wartością natężenia pola a potencjałem możemy zapisać następującą zależność:

gdzie:

E - natężenia pola

V - potencjał pola

Wartość natężenia pola elektrostatycznego można wyrazić jako stosunek spadku potencjału -ΔV na niewielkim odcinku prostopadłym do powierzchni ekwipotencjalnej (powierzchnia równego potencjału) do długości Δl tego odcinka. Znak „ - ” wynika stąd, że zwrot wektora E jest przeciwny do spadku potencjału.

Gęstość powierzchniowa ładunku i jej związek z natężeniem pola

Wszystkie ładunki znajdujące się na powierzchni jakiegoś naładowanego przewodnika rozmieszczone są z różną gęstością powierzchniową. Gęstość powierzchniową ładunku określamy jako:

gdzie:

- gęstość powierzchniowa

Δq - ładunek elektryczny znajdujący się elementarnej powierzchni

ΔS - elementarna powierzchnia

Za pomocą związku między gęstością powierzchniową ładunku a natężeniem pola możemy obliczyć gęstość powierzchniową na podstawie znajomości natężenie pola.

Dla kondensatora gęstość powierzchniowa wyrażać się będzie wzorem:

gdzie:

- gęstość powierzchniowa

V₁ - wartość potencjału na pierwszej płytce kondensatora

V₂ - wartość potencjału na drugiej płytce kondensatora

d - odległość okładek kondensatora od siebie

E - natężenie pola elektrycznego

= 8,85·10^-12 [F/m] - przenikalność elektryczna próżni

II Przyrządy potrzebne do doświadczenia:

• dwie płytkie kondensatora

• sonda płomykowa

• zasilacz wysokiego napięcia WN

• woltomierz

III Przebieg doświadczenia

Doświadczenie miało na celu zbadanie natężenia pola elektrycznego między okładkami kondensatora przy pomocy sondy płomykowej.

1. Ustawiliśmy prawą płytkę kondensatora w odległości d₁=40 mm od lewej płytki

2. Zapaliliśmy sondę płomykową

3. Załączyliśmy zasilacz woltomierza i zasilacz WN

4. Przesuwaliśmy sondę do położenia, w którym wskaźnik woltomierza pokazał 600 V

5. Dokonaliśmy serii pomiarów przesuwając sondę w kierunku prawej płytki co 2mm wykonując pomiar potencjału.

6. Następnie dokonaliśmy pomiarów dla odległości d₂=80 mm i d₃=120 mm, przesuwając sondę płomykową co 3 mm (po wcześniejszym ustawieniu sondy płomykowej w miejscu, w którym woltomierz wskazał 600 V).

7. Wyniki pomiarów zamieszczamy w Tabelce 1.

Tabela 1. Tabela wyników pomiarów

d1=40 mm		d2=80 mm		d3=120 mm
U	l	U	l	U	l
[V]	[mm]	[V]	[mm]	[V]	[mm]
600	7	600	17	600	35
750	9	680	20	660	38
900	11	800	23	720	41
1060	13	920	26	800	44
1240	15	1040	29	860	47
1400	17	1160	32	920	50
1580	19	1280	35	980	53
1740	21	1400	38	1040	56
1920	23	1540	41	1100	59
2100	25	1680	44	1200	62
2280	27	1820	47	1260	65
2460	29	1960	50	1320	68
2620	31	2080	53	1440	71
2760	33	2260	56	1520	74
2900	35	2380	59	1600	77
3000	37	2540	62	1720	80
		2700	65	1800	83
		2820	68	1940	86
		2980	71	2040	89
				2180	92
				2220	95
				2300	98
				2440	101
				2540	104
				2680	107
				2760	110
				2920	113

Zależność potencjału V w funkcji odległości l dla kondensatora powietrznego jest funkcją liniową określoną wzorem
.

Prosta o równaniu y=ax+b jest wykresem funkcji. Współczynnik kierunkowy „a” jest równy natężeniu pola elektrycznego E.

Wykresy zależności U= f(l)

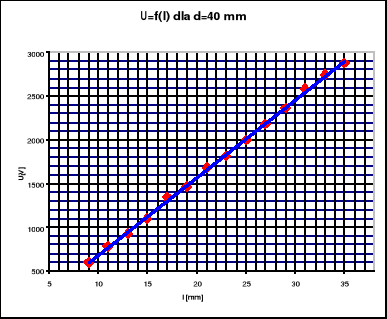
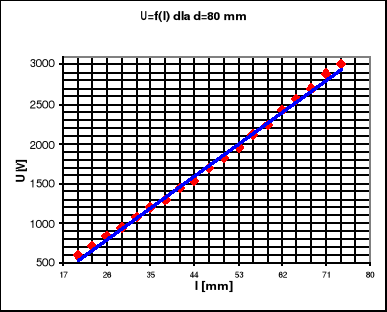
Arkusz kalkulacyjny dostępny na pracowni, posłużył nam do obliczenia współczynników a i b prostych regresji dopasowanych do wykreślonych zależności.

	Parametry prostej regresji
Odległość płytek - d		a =Ed	a	b [V]	b [V]
d1=40 mm		83,2	0,8	1,83	19,9
d1=80 mm		44,7	0,55	-249	26
d1=120 mm		29,6	0,66	-575	51

Wzór:

posłużył nam do obliczenia teoretycznych wartości natężenia pola elektrycznego E_t dla poszczególnych wartości d i zadanego napięcia między płytkami kondensatora. Wartość napięcia odczytaliśmy z zasilacz WN: U=3000 V.

Wartości teoretyczne dla:

• d₁=40 mm
  

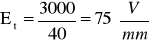
• d₁=80 mm
  

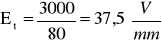
• d₁=120 mm
  

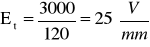
Obliczyliśmy względne odchylenia δ wartości doświadczalnych natężenia pola elektrycznego E_d od wartości teoretycznych E_t. Wynik wyrażony jest procentach.

Korzystając ze wzoru:

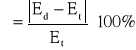
otrzymujemy następujące wyniki dla poszczególnych odległości d_x:

• d₁=40 mm
  

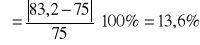
• d₁=40 mm
  

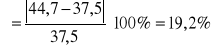
• d₁=40 mm
  

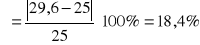
Tabela 2 zawiera zestawienie wyników obliczeń

Tabela 2. Wyniki obliczeń

d1=40 mm			d2=80 mm			d3=120 mm
Ed [V/mm]	Et [V/mm]	δ [%]	Ed [V/mm]	Et [V/mm]	δ [%]		Ed [V/mm]	Et [V/mm]	δ [%]
83,2	75	13,6	44,7	37,5	19,2		29,6	25	18,4

Obliczyliśmy gęstość powierzchniową ładunku σ_d na wewnętrznej powierzchni jednej z płytek.

Wyniki dwóch pierwszych doświadczeń(d₁=40 mm, d₂=80 mm) tworzą liniową zależność U=f(l).Gęstość powierzchniową liczymy z następującego wzoru:

σ = ε_r ^. ε₀ ^. E_d

gdzie:

σ - gęstość powierzchniowa

ε_r = 1,0006 - przenikalność elektryczna powietrza

ε₀ =8,85^.10^-15[F/mm] - przenikalność elektryczna próżni

Wyniki dla poszczególnych długości wynoszą:

• dla d₁=40 mm σ =
  

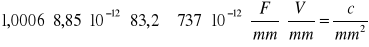
• dla d₂=80 mm σ =
  

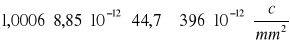
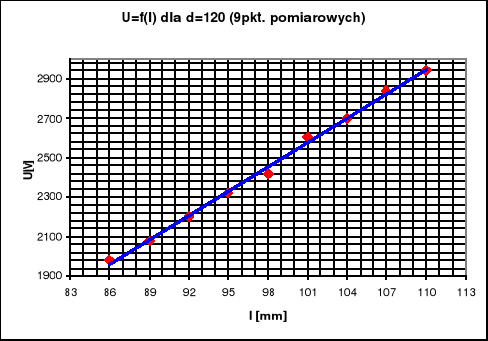
W doświadczeniu 3 (dla d₃=120 mm) wykres zależności U=f(l) odbiega od linii prostej. W celu obliczenie gęstości wyznaczyliśmy parametry prostej regresji dopasowanej do ostatnich 9-ciu punktów pomiarowych znajdujących się w pobliżu prawej płytki kondensatora. Parametr „a” określa lokalne natężenie pola elektrycznego E_dl.

Wykorzystując arkusz kalkulacyjny obliczyliśmy, że parametr jest równy 41,2. Wartość E_dl=41,2 [V/mm]. Z wzoru:
,gdzie
= 8,85·10^-12 [F/m] - przenikalność elektryczna próżni

Gęstość powierzchniowa wynosi:

σ =

Policzyliśmy w 3 przypadkach liczbę elektronów przypadającą na 1 mm² powierzchni płytki. Uzyskaliśmy go dzieląc obliczone wartości σ przez ładunek elementarny e = 1,602·10^-19 C = 1,602·10^-13 μC

• 737· 10¹²:1,602·10^-13 = 460,05·10²⁵
  

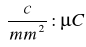
• 396· 10¹²:1,602·10^-13= 247,19·10²⁵
  

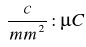
• 365· 10¹² :1,602·10^-13= 227,84·10²⁵
  

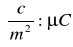
Tabela 3 zestawia wyniki obliczeń natężenia pola elektrycznego i gęstości powierzchniowej ładunku dla poszczególnych odległości.

Tabela 3. Wyniki obliczeń

d1=40 mm		d2=80 mm		d3=120 mm
Ed [V/mm]	σ x 10^-7[ μC/mm^2 ]	Edl [V/mm]	σ x 10^-7[μC/mm^2 ]	Edl [V/mm]	σ x 10^-7[μC/mm^2 ]
83,2	7,37	44,7	3,96	41,2	3,65

IV Wnioski:

Dla płytek o odległościach równych d₁₌ 40 mm oraz d₂= 80 mm zależności U=f(l) tworzą zależność liniową.

Odchylenia od prostej regresji są niewielkie.

Dla odległości 120mm odchylenia od prostej regresji są dosyć duże. Powodem tego może być to, że w pobliżu płytek pole elektryczne jest duże, a w miarę oddalania się od nich maleje

Wielkości zmierzone bezpośrednio i obliczone, są obarczone błędem, który może wynikać przyrządów:

• niedokładności przyrządów służących do wykonywania pomiarów

• niedokładnego ustawienia płytek kondensatora i sondy między okładkami kondensatora

• niejednorodności pola elektrycznego. Odległość między okładkami jest zbliżona do wymiarów okładek, więc natężenie pola między okładkami nie jest jednorodne.

.

---