ANALIZA WSPÓŁZALEŻNOŚCI ZJAWISK

Wstęp

Badanie zależności między zjawiskami i procesami masowymi jest jednym z naj-istotniejszych zagadnień w każdej dziedzinie wiedzy.

Umożliwia ono poznawanie występujących między nimi związków przyczynowo-skutkowych, będących podstawą przewidywania dalszego ich rozwoju. Nie wystarczy przy tym stwierdzić, że poziom danego zjawiska ulega zmianie wraz ze zmianą innego zjawiska bądź innych zjawisk. Konieczne jest sięganie do bardziej precyzyjnych narzędzi badania związków między zjawiskami, pozwalających skwantyfikować zależności między nimi.

Wykrywaniem i numerycznym ujmowaniem związków między zmiennymi reprezentującymi zjawiska masowe zajmuje się rachunek korelacji i regresji.

Zakres rzeczowy tej metody obejmuje dwa człony:

1. Rachunek korelacji, który zajmuje się badaniem siły i kierunku zależności między zmiennymi. Służą do tego celu różnego rodzaju miary korelacji.

W szczególności są to:

• współczynnik korelacji liniowej Pearsona, który jest stosowany, gdy:

− badamy zależność między dwiema zmiennymi mierzalnymi,

− badany związek korelacyjny uznamy za liniowy,

• współczynnik korelacji rang Spearmanna, stosowany, gdy:

− badamy zależność między dwiema cechami,

− poszczególnym kategoriom badanych cech można nadać rangi, czyli można „ustawić” je według hierarchii ważności,

• współczynnik kontyngencji i współczynnik Czuprowa, stosowane, gdy:

− analizujemy zależność między cechami niemierzalnymi.

2. Rachunek regresji, który, zajmuje się problematyką funkcyjnego odwzorowania zależności między badanymi zmiennymi.

Jego zadaniem jest poszukiwanie określonej klasy funkcji, która w możliwie najlepszy sposób charakteryzowałaby zależność między zmiennymi. Funkcję tą określa się mianem funkcji regresji.

Statystyczne badanie związków między zmiennymi opiera się na pojęciu tzw. związku korelacyjnego.

Jego istota sprowadza się do tego, że poszczególnym wartościom jednej cechy można przyporządkować średnią wartość drugiej cechy (ograniczając interpretację do relacji dwuwymiarowej).

Oznacza to, że pojęcie związku korelacyjnego różni się zasadniczo od pojęcia związku funkcyjnego.

Związek funkcyjny charakteryzuje się bowiem tym, że każdej wartości zmiennej niezależnej X odpowiada jedna, jednoznacznie określona wartość zmiennej zależnej Y.

Warto zwrócić uwagę na fakt, że stwierdzenie związku korelacyjnego między zmiennymi nie musi wcale oznaczać występowania pomiędzy nimi zależności przyczynowo-skutkowej. Może tak być, ale nie musi. Żeby tak było, konieczna jest dogłębna analiza merytoryczna.

W przypadku badania zależności między dwiema zmiennymi mierzalnymi najprostszym sposobem ujawnienia związku korelacyjnego jest sporządzenie tzw. diagramu korelacyjnego. Na jego podstawie można wnioskować:

• czy związek korelacyjny występuje, czy też go nie ma?

• jaki jest kierunek związku korelacyjnego?

• czy związek korelacyjny jest silny, czy słaby?

• jaki jest kształt funkcyjny zależności korelacyjnej?

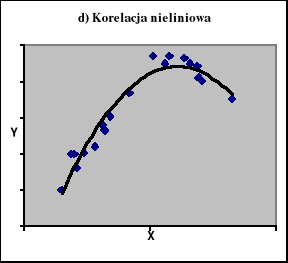
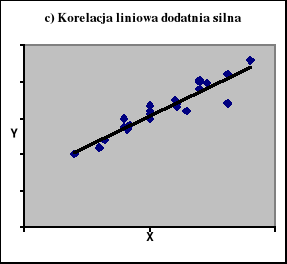
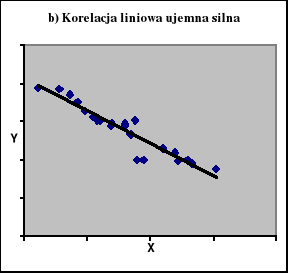
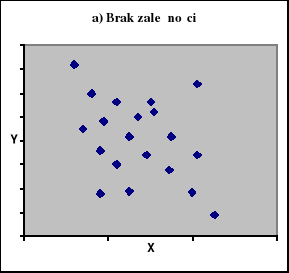
Na ryc. 1 zaprezentowano diagramy korelacyjne z jakimi możemy mieć do czynienia analizując zależności miedzy dwiema zmiennymi mierzalnymi.

W przypadku natomiast badania zależności między wieloma zmiennymi mierzalnymi, postępujemy pragmatycznie, przyjmując hipotezę, że jest to zależność liniowa. U podstaw takiego postępowania leży następujące rozumowanie.

Analizując zależności wielowymiarowe nie jesteśmy w stanie określić w sposób jednoznaczny postaci analitycznej funkcji regresji, argumentów za tym nie dostarcza bowiem ani teoria ani analiza wyników obserwacji.

Tym właśnie można tłumaczyć, dlaczego hipoteza o liniowości funkcji regresji jest najczęściej przyjmowana.

Ryc. 1

Korelacja między dwiema zmiennymi mierzalnymi

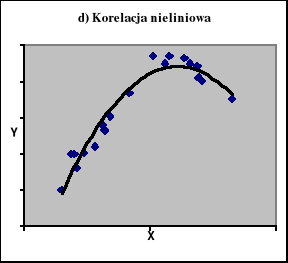
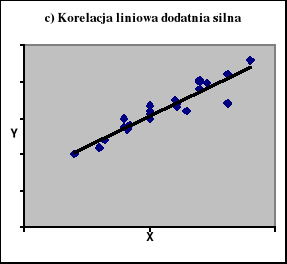
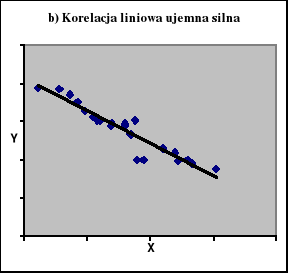
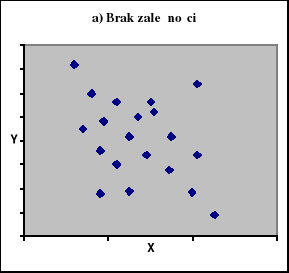
Źródło: Zestawienie własne.

Mierniki korelacji dwóch zmiennych

Współczynnik korelacji liniowej Pearsona

W analizie korelacji jednakowo traktujemy obie zmienne: zmienną objaśnianą i zmienną objaśniającą. Przyjmujemy wtedy założenie, że obie zmienne są zmiennymi losowymi. Badanie związku w tym nowym układzie to właśnie analiza korelacji. Silnie skorelowane ze sobą zmienne zachowują się tak, jak gdyby równocześnie się poruszały. W przypadku, gdy pomiędzy badanymi zmiennymi zachodzi związek liniowy, wówczas miarą siły i kierunku korelacji miedzy nimi jest współczynnik korelacji Pearsona r_xy.

O związku liniowym między zmiennymi mówimy wówczas, gdy jednostkowym przyrostom przyczyny (zmiennej niezależnej) towarzyszy stały przyrost skutku (zmiennej zależnej).

Współczynnik korelacji wyznacza się przez standaryzację kowariancji. Kowariancja natomiast jest średnią arytmetyczną iloczynu odchyleń zmiennych X i Y od wartości ich średnich arytmetycznych:

.

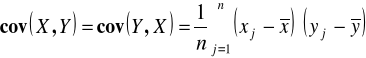
Kowariancja informuje o:

• braku zależności korelacyjnej gdy cov (X,Y) = 0 ,

• ujemnej zależności korelacyjnej gdy cov (X,Y) < 0,

• dodatniej zależności korelacyjnej gdy cov (X,Y) > 0.

Równocześnie :
.

Ostatecznie więc unormowanym miernikiem natężenia związku dwóch zmiennych jest współczynnik korelacji r :

.

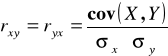
Współczynnik korelacji liniowej jest to stosunek sumy iloczynu odchyleń poszczególnych wartości zmiennych X i Y od ich średnich arytmetycznych do iloczynu odchyleń standardowych obydwu zmiennych i ogólnej liczebności zbiorowości (próby).

Można go więc zapisać następująco:

.

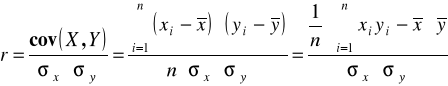
Współczynnik ten, jak już zapisaliśmy wcześniej, jest wielkością unormowaną, przyjmuje wartości z przedziału
:

r =1 − korelacja dodatnia, związek funkcyjny,

0 < r < 1 − korelacja dodatnia niedoskonała,

r = 0 − brak korelacji liniowej,

-1 < r < 0 − korelacja ujemna niedoskonała,

r = -1 − korelacja ujemna, związek funkcyjny.

Przykład.

Dla 15 gospodarstw domowych 4-osobowych zebrano informacje o przychodach miesięcznych (w zł/1 osobę) i wysokości wydatków na utrzymanie mieszkania (w zł/1osobę ) w I półroczu 2007 r.:

X	594	450	395	520	648	695	825	800	687	650	430	874	808	609	765
Y	58	48	42	62	70	75	95	92	66	72	45	88	85	65	74

Y - wydatki na utrzymanie mieszkania w przeliczeniu na 1 osobę

X - przychody miesięczne w zł / 1osobę

Określ siłę i kierunek zależności między tymi zmiennymi.

Rozwiązanie.

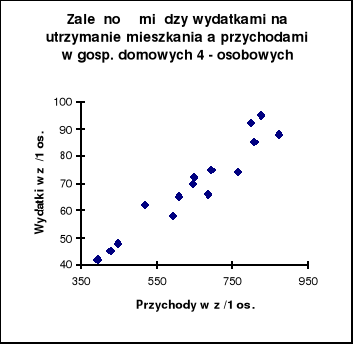
W celu sprawdzenia, czy zależność między tymi zmiennymi można uznać za liniową sporządzamy korelacyjny diagram rozrzutu.

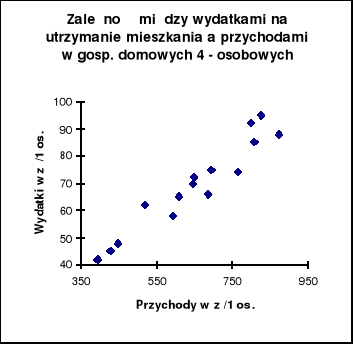
Jak wynika z wykresu zależność można uznać za liniową, wykres wskazuje też, że jest to zależność dodatnia i prawdopodobnie silna.

W związku z tym możemy liczyć współczynnik korelacji liniowej Pearsona. Wyliczymy go według wzoru:

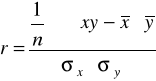
Obliczenia pomocnicze wykonane w oparciu o wyniki uzyskane w tabeli roboczej:

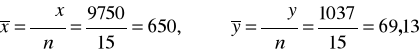
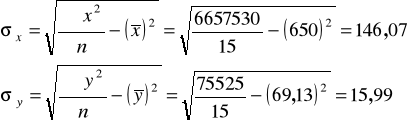
Podstawiamy do wzoru na r :

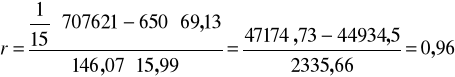
Tabela robocza:

xi	yi
594 450 395 520 648 695 825 800 687 650 430 874 808 609 765	58 48 42 62 70 75 95 92 66 72 45 88 85 65 74	352836 202500 156025 270400 419904 483025 680625 640000 471969 422500 184900 763876 652864 370881 585225	3364 2304 1764 3844 4900 5625 9025 8464 4356 5184 2025 7744 7225 4225 5476	34452 21600 16590 32240 45360 52125 78375 73600 45342 46800 19350 76912 68680 39585 56610
9750	1037	6657530	75525	707621

Źródło: Obliczenia własne.

Odpowiedź:

Między wydatkami na utrzymanie mieszkania a dochodem w przeliczeniu na 1 osobę występuje bardzo silna zależność o kierunku dodatnim.

Korelacja rang

W przypadku mało licznych zbiorowości sklasyfikowanych ze względu na dwie cechy, pomiędzy którymi chcemy zbadać współzależność, możliwe staje się zastosowanie do pomiaru siły i kierunku tej współzależności współczynnika korelacji rang Spearmana.

Miarę tą obliczamy wg wzoru :

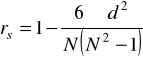
gdzie:

N − liczebność zbiorowości,

d − różnica rang między odpowiadającymi sobie wariantami cech X i Y.

Łatwo zauważyć, że miarę tę stosować można, gdy możliwe jest określenie hierarchii ważności wariantów badanych cech, co pozwala na nadanie im rang.

Ponadto, obliczenie tego współczynnika wymaga uporządkowania par wariantów cech X i Y wg wariantów cechy X, tj. tej zmiennej, która jest zmienną niezależną.

Współczynnik korelacji rang przyjmuje wartości z przedziału < -1; +1 >, a jego interpretacja przebiega podobnie jak współczynnika korelacji liniowej Pearsona.

Jeśli więc
= 0, to korelacja nie występuje.

Jeśli
, to mówimy o korelacji dodatniej.

Gdy natomiast
, to związek korelacyjny między zmiennymi jest ujemny.

Przykład.

Dla 10 pracowniczych gospodarstw domowych zebrano następujące informacje dotyczące przeciętnego miesięcznego dochodu na 1 osobę w zł oraz wysokości wydatków miesięcznych na 1 osobę na owoce w zł w 2007 r. Dane te zawarto w tabeli:

Dochód w zł	600	750	800	640	490	1020	840	780	520	600
Wydatki na owoce w zł	7,5	10,0	10,0	7,4	6,5	18,5	10,5	9,5	6,4	7,0

Określ siłę i kierunek zależności między tymi zmiennymi stosując współczynnik korelacji rang Spearmana.

Rozwiązanie:

Przyjmujemy, że wysokość wydatków na owoce zależy od dochodu, stąd:

X - dochód miesięczny na 1 osobę w zł,

Y - wysokość wydatków na owoce na 1 osobę w zł.

Porządkujemy gospodarstwa domowe rosnąco według wartości dochodu:

Dochód	Wydatki	Rangi
					Rx	Ry
490 520 600 600 640 750 780 800 840 1020	6,5 6,4 7,0 7,5 7,4 10,0 9,5 10,0 10,5 18,5	1 2 3,5 3,5 5 6 7 8 9 10	2 1 3 5 4 7,5 6 7,5 9 10	(1 - 2)^2 = 1 (2 -1)^2 = 1 (3,5 - 3)^2 = 0,25 (3,5 - 5)^2 = 2,25 (5 - 4)^2 = 1 (6 - 7,5)^2 = 2,25 (7 - 6)^2 = 1 (8 - 7,5)^2 = 0,25 (9 - 9)^2 = 0 (10 - 10)^2 = 0
X	X	X	X	9

Źródło: Obliczenia własne na podstawie danych umownych.

Podstawiamy do wzoru i otrzymujemy:

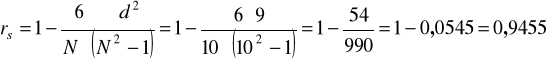
Odpowiedź:

Między wydatkami na owoce a dochodem na 1 osobę występuje bardzo silna zależność dodatnia.

1

8

---