WYMIAROWANIE KONSTRUKCJI MUROWYCH

• ŚCIANY OBCIĄŻONE GŁÓWNIE PIONOWO

Obciążenie pionowe ścian obciążonych głównie pionowo stanowią:

• ciężar własny,

• obciążenie pionowe od stropów (w tym również od dachów, schodów i balkonów) i ścian opartych na rozpatrywanej ścianie, a także siły wewnętrzne, wynikłe z połączenia ściany rozpatrywanej ze ścianami przyległymi, jeżeli ich odkształcenie pionowe jest znacząco różne od odkształcenia ściany rozpatrywanej.

Poza obciążeniem pionowym występować może również oddziaływujące bezpośrednio na ścianę obciążenie poziome, prostopadłe do płaszczyzny ściany (parcie gruntu, oddziaływanie wiatru), ale efekt oddziaływań poziomych ma drugorzędne znaczenie..

Obciążenie pionowe od stropów wyznacza się zgodnie z zasadami podanymi na rysunku 3b) lub zastępczo - obciążenie z pasma stropu o szerokości równej 0,3 rozpiętości stropu.

Rys. 3 - Rozdział obciążenia ze stropu na ściany konstrukcyjne: a) strop zbrojony jednokierunkowo, b) strop zbrojony jednokierunkowo, przylegający do ściany samonośnej, c) strop zbrojony dwukierunkowo, oparty na trzech ścianach nośnych, d) strop zbrojony dwukierunkowo, oparty na czterech ścianach nośnych; strzałkami oznaczono kierunek rozpięcia zbrojenia stropu

Stan graniczny nośności ścian obciążonych głównie pionowo sprawdzać należy z warunku:

N_Sd ≤ N_Rd

w którym:

N_Sd - obliczeniowe obciążenie pionowe ściany

N_Rd - nośność obliczeniowa ściany ze względu na obciążenie pionowe.

Sprawdzenia nośności należy dokonać w przekrojach:

• pod stropem,

• nad stropem,

• w środkowej strefie ściany.

Uwzględnić należy:

• geometrię ścian,

• mimośrodowe działanie obciążenia pionowego,

• właściwości materiałowe muru.

W ścianach z otworami sprawdzić należy także nośność nadproży.

Przy wyznaczaniu miejsca przyłożenia obliczeniowego obciążenia pionowego N_Sd należy uwzględnić niezamierzony mimośród przypadkowy e_a = h/300 (h w mm - wysokość ściany w świetle), lecz nie mniej niż 10 mm.

Nośność obliczeniową ściany wyznacza się:

• w przekroju pod stropem górnej kondygnacji N_1R,d oraz w przekroju nad stropem dolnej kondygnacji N_2R,d ze wzoru

N_iR,d = Φ_i A f_d (15)

w którym:

i = 1 dla przekroju pod stropem oraz i = 2 dla przekroju nad stropem;

Φ_i - współczynnik redukcyjny, zależny od wielkości mimośrodu e_i, na którym w rozpatrywanym przekroju działa obliczeniowa siła pionowa N_Sd, oraz od wielkości mimośrodu niezamierzonego e_a;

A - pole przekroju;

f_d - wytrzymałość obliczeniowa muru na ściskanie,

• w środkowej strefie ściany - ze wzoru

N_mR,d = Φ_m A f_d (16)

w którym:

Φ_m - współczynnik redukcyjny wyrażający wpływ efektów drugiego rzędu na nośność ściany, zależny od:

• wielkości mimośrodu początkowego e_o = e_m,

• smukłości ściany h_eff/t,

• zależności σ(ε) muru,

• czasu działania obciążenia.

Wysokość efektywna ściany h_eff uwzględnia warunki połączenia ściany ze stropem, a także usztywnienie ściany ścianami usytuowanymi do niej prostopadle.

ZASADY PRZYJMOWANIA WYSOKOŚCI EFEKTYWNEJ

Wysokość efektywną ściany oblicza się ze wzoru:

h_eff = ρ_h ∙ ρ_n ∙ h

w którym:

ρ_h - odpowiednio do przestrzennego usztywnienia budynku wg tablicy 17 (NORMA)

ρ_n - odpowiednio do usztywnienia ściany wzdłuż dwóch, trzech lub czterech krawędzi

Tablica 17 - Wartości współczynników ρ_h

Rodzaj konstrukcji z uwagi na usztywnienie przestrzenne		Rodzaj stropów
				z betonu z wieńcami żelbetowymi	inne
Konstrukcja usztywniona przestrzennie w sposób eliminujący przesuw poziomy		1,0	1,25
Konstrukcja bez ścian usztywniających, przy czym liczba ścian prostopadłych do kierunku działania obciążenia poziomego, przejmujących to obciążenie wynosi	3 i więcej	11,25	1,50
		2	1,50	2,0
Ściany wolno stojące		2,0

Ściany uważać można za usztywnione wzdłuż krawędzi pionowej, jeżeli:

• połączone są wiązaniem murarskim lub za pomocą zbrojenia ze ścianami usztywniającymi usytuowanymi do nich prostopadle, wykonanymi z muru o podobnych właściwościach odkształceniowych

• długość ścian usztywniających jest nie mniejsza niż 0,2 wysokości ściany, a grubość nie mniejsza niż 0,3 grubości ściany usztywnianej i nie mniejsza niż 100 mm.

W przypadku ściany usztywniającej z otworami, zaleca się, aby długość części ściany między otworami, przyległej do ściany usztywnianej była nie mniejsza niż podano na rysunku 6, a ściana usztywniająca sięgała poza otwór na długość nie mniejszą niż 1/5 wysokości kondygnacji.

Rysunek 6 - Minimalna długość ściany usztywniającej z otworami

Alternatywnie - ściany mogą być usztywniane przez inne elementy niż ściany murowane pod warunkiem, że sztywność tych elementów jest równoważna ze sztywnością murowanej ścianie usztywniającej, o której mowa powyżej, a obie ściany połączone są ze ścianą usztywnianą za pomocą ściągów lub kotew, zaprojektowanych tak, aby zdolne były przenieść siły ściskające lub rozciągające, które mogą się pojawić w połączeniu.

Za wartość ρ_n przyjmować można:

a) dla ścian podpartych u góry i u dołu, w przypadku posługiwania się:

• modelem ciągłym - ρ₂ = 0,75;

• modelem przegubowym - ρ₂ = 1,00;

b) dla ścian podpartych u góry i u dołu i usztywnionych wzdłuż jednej krawędzi pionowej (z jedną swobodną krawędzią pionową):

• jeżeli h ≤ 3,5 L, wartość obliczoną ze wzoru:

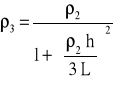
w którym:

ρ₂ - jak podano wyżej;

- jeżeli h > 3,5 L, wartość obliczoną ze wzoru:

w którym:

L - odległość krawędzi swobodnej od osi ściany usztywniającej;

c) dla ścian podpartych u góry i u dołu oraz wzdłuż obu krawędzi pionowych:

• jeżeli h ≤ L, wartość obliczoną ze wzoru:

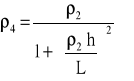
w którym:

ρ₂ - jak podano w a) powyżej lub

• jeżeli h > L, wartość obliczoną ze wzoru:

W przypadku, gdy ściany są usztywnione wzdłuż obu krawędzi pionowych i L ≥ 30t lub gdy ściany są usztywnione wzdłuż jednej krawędzi i L ≥ 15 t, gdzie t jest grubością ściany usztywnionej - ściany takie należy uważać za ściany usztywnione tylko u góry i u dołu.

Zaleca się, aby smukłość h_eff / i (lub wyrażona jako h_eff / t) ścian konstrukcyjnych była nie większa niż:

87,5 (25) - w przypadku ścian z murów na zaprawie f_m ≥ 5 MPa, z wyjątkiem murów z bloczków komórkowego;

63 (18) - w przypadku ścian z bloczków z betonu komórkowego, niezależnie od rodzaju zaprawy, a także dla murów z innego rodzaju elementów murowych, na zaprawie f_m < 5 MPa.

ZASADY OBLICZENIOWE

W zależności od warunków przekazywania w poziomie stropu, siły pionowej ze ściany górnej kondygnacji dolną, do wyznaczenia wielkości mimośrodu e_i względnie e_m posługiwać się należy:

• modelem ciągłym, w którym ściana stanowi pręt pionowy ramy połączony z prętami poziomymi, obrazującymi stropy lub

• modelem przegubowym, w którym ściana stanowi wydzielony pręt podparty przegubowo w poziomie stropów.

Modelem ciągłym można się posługiwać, kiedy stropy żelbetowe lub sprężone oparte są na ścianie za pośrednictwem wieńca żelbetowego szerokości równej grubości ściany lub nie mniejszej niż grubość stropu, średnie ściskające naprężenie obliczeniowe ściany σ_cd ≥ 0,25 MPa, a mimośród e₁ działania obciążenia pionowego w przekroju ściany pod stropem e₁ ≤ 0,33 (t - grubość ściany).

Przy wyznaczaniu wielkości e_i lub e_m należy także uwzględniać obciążenie poziome, oddziaływujące bezpośrednio na rozpatrywaną ścianę.

1. MODEL CIĄGŁY

Przy posługiwaniu się modelem ciągłym współczynnik Φ_i wyznacza się odpowiednio do wartości mimośrodu e_i działania obciążenia pionowego, którą obliczać można ze wzoru:

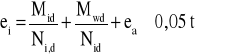
w którym:

t - grubość ściany

M_id - obliczeniowy moment zginający w przekroju ściany pod stropem (M_1d) lub nad stropem (M_2d), wynikły z obciążenia ściany stropem,

N_i,d - obliczeniowa siła pionowa w rozpatrywanym przekroju,

M_wd - obliczeniowy moment zginający, wywołany obliczeniowym obciążeniem poziomym oddziaływującym bezpośrednio na ścianę,

e_a - mimośród przypadkowy (e_a = h/300, gdzie h w mm - wysokość          ściany w świetle, lecz nie mniej niż 10 mm.

Wartość momentu M_id wyznaczać można dla każdego z węzłów ramy oddzielnie, przyjmując w uproszczeniu, że schodzące się w węźle ściany i strop są niezarysowane i zachowują się liniowo sprężyście.

Odkształcenia plastyczne zachodzące w węźle ściana-strop można uwzględniać, redukując wartości momentu zginającego w przekroju ściany nad i pod stropem, odpowiednio do wyników badania zachowania się węzła ramy pod obciążeniem obliczeniowym stropu i obciążeniem ściany nie mniejszym niż 0,6 jej nośności oblicze­niowej.

Jeżeli duża dokładność obliczeń nie jest potrzebna, a szerokość wieńca za pośrednictwem którego strop opiera się na ścianie jest nie mniejsza niż grubość ściany lub wysokość przekroju stropu - obowiązuje wartość mniejsza - do obliczeń przyjąć można moment zginający w przekroju nad i pod stropem równy 0,85 wartości uzyskanej z analizy sprężystej ramy.

Rysunek 4 - Model ciągły - wyznaczanie wartości momentów M_1d i M_2d

a) zewnętrzna ściana nośna, b) momenty wywołane mimośrodowym obciążeniem ściany stropa­mi i uproszczone modele obliczeniowe do wyznaczania wartości M_id

Jeżeli obciążenie obliczeniowe stropu jest równomiernie rozłożone i wynosi q_d, moment M_1d w przekroju ściany pod stropem wyznaczać można:

• dla ściany obciążonej jednostronnie

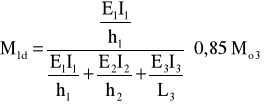
• dla ściany obciążonej obustronnie

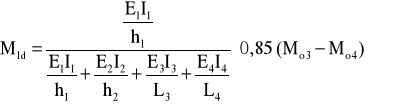
W przypadku, kiedy obciążenie stropu o rozpiętości L₃ jest równomiernie rozłożone i wynosi q_d, moment węzłowy M_o równa się:

- dla przęsła o rozpiętości L₃

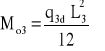
- dla przęsła o rozpiętości L₄

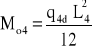
Jeżeli duża dokładność obliczeń nie jest wymagana, moment zginający występujący na podporze stropu 0,85M_o3 można rozdzielić proporcjonalnie do sztywności ścian w rozpatrywanym węźle ramy.

Wartość M_wd należy wyznaczać jak dla belki ciągłej.

Kiedy oddziaływujące bezpośrednio na ścianę obliczeniowe obciążenie poziome jest obciążeniem równomiernie rozłożonym w_d, za wartość M_wd przyjmować można:

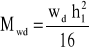
Kiedy zależność σ(ε) murów można wyrazić za pomocą „paraboli madryckiej" lub podobnej funkcji, tak jak to ma miejsce z reguły w przypadku murów z elementów grupy 1 i 2 (por. 4.7), wartość współczynnika Φ_i przyjmuje się równą:

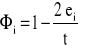
Dla murów z elementów grupy 3, których zależność σ(ε) z reguły nie ma półki poziomej zaleca się przyjmować

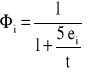
Wartość współczynnika Φ_i wyznacza się jak dla pręta podpartego przegubowo o wysokości efektywnej h_eff wyznaczonej zgodnie z p. 5.1.4, obciążonego siłą N_md działającą na mimośrodzie e_m, równym co do wartości u góry i u dołu ściany.

Wielkość mimośrodu e_m oblicza się w takim przypadku ze wzoru:

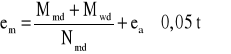
w którym:

M_md - największy moment obliczeniowy w środkowej 1/5 wysokości ściany, zależny od wartości M_1d i M_2d jak zaznaczono na rysunku 4b; wartości momentów M_1d i M_2d oblicza się ze wzoru (18);

M_wd - moment zginający w połowie wysokości ściany, wywołany przez obliczeniowe obciążenie pozio­me, oddziaływujące bezpośrednio na ścianę;

N_md - obliczeniowa siła pionowa w połowie wysokości ściany.

Wpływ długotrwałego działania obciążenia na nośność ściany uwzględnia się, przyjmując do wyznaczenia wartości Φ_m długotrwały moduł sprężystości muru E_∞ określony wzorem (13). Jeżeli duża dokładność obliczeń nie jest wymagana, przyjąć można η_E = 0,3 i
= 1,5. W związku z tym, za parametr
przyjmuje się:

• dla murów na zaprawie f_m ≥ 5 MPa, z wyjątkiem murów z bloczków z betonu komórkowego
  ;

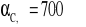
• dla murów na zaprawie f_m < 5 MPa i dla murów z bloczków z betonu komórkowego, niezależnie od rodzaju zaprawy
  .

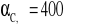
W przypadku ścian o przekroju prostokątnym wartości Φ_m przyjmuje się z Tablicy 16 odpowiednio do wartości współczynnika smukłości h_eff/t i współczynnika sprężystości
wyznaczonego dla
i
.

Jeżeli przyjmuje się inne wartości
i
wartości Φ_m przyjmuje się z tablicy 16 dla
i h_eff/t i mnoży przez 0,0316
, gdzie
jak we wzorze (13).

Wartości Φ_m podane w tablicy 16 odnoszą się do murów z elementów wszystkich trzech grup, z tym, że dla murów z elementów grupy 3 obowiązuje warunek:

Φ_m≤Φ_i (26)

w którym:

Φ_i - ze wzoru (24)

W przypadku ścian o przekroju innym niż prostokątny, również przyjmuje się wartości Φ_m z tablicy 16, dla współczynnika smukłości o wartość 2 h_eff/2y, gdzie: y - odległość środka ciężkości pola przekroju ściany od krawędzi bardziej ściskanej.

5.1.3 MODEL PRZEGUBOWY

Przy posługiwaniu się modelem przegubowym (rysunek 5a) do obliczania ściany przyjąć można:

a) na najwyższej kondygnacji:

• w przekroju pod stropem siła z dachu N_1d działa w stosunku do nominalnej osi ściany na mimośrodzie e_a, a obciążenie od stropu N_S|,_d - na mimośrodzie 0,41 + e_a;

• w przekroju nad stropem dolnej kondygnacji siła N_2d, stanowiąca sumę N_1d i N_s,_id ciężaru ściany, działa na mimośrodzie e_a;

b) dla ścian niższych kondygnacji:

• w przekroju pod stropem siła z górnych kondygnacji N_1d działa na mimośrodzie e_a, a obciążenie od stropu N_s!id - na mimośrodzie 0,33 t + e_a;

• w przekroju nad stropem dolnej kondygnacji - analogicznie jak w przypadku ściany najwyższej kondygnacji.

Rysunek 5 - Model przegubowy ściany zewnętrznej: a) ściana najwyższej kondygnacji, b) ściana niższych kondygnacji

W związku z powyższym, nośność ściany najwyższej kondygnacji sprawdza się w przekroju pod stropem górnej kondygnacji - na moment M_1d, a w przekroju nad stropem dolnej kondygnacji - na moment M_2d, równe

M_1d = N_1d · e_a + N_sl,d · (0,4 t + e_a)

M_2d = N_2d · e_a

a nośność ściany niższych kondygnacji - na moment M_1d i M_2d, równe

M_1d = N_1d · e_a + N_sl,_d · (0,33 t + e_a)

M_2d = N_2d · e_a

Aby skorzystać z wartości Φ_m podanych w tablicy 16 wyznacza się zastępczy mimośród początkowy e_m, równy co do wartości u góry i u dołu modelowego pręta ściany (rysunek 5b). Wartość tego mimośrodu wynosi:

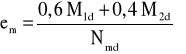
w którym:

M_1d i M_2d - ze wzoru (27) ÷ (30);

N_md - obliczeniowa siła pionowa w połowie wysokości ściany;

i dla tej wartości e_m znajduje się - zgodnie z zasadami podanymi w 5.1.2 - odpowiednią wartość Φ_m.

Jeżeli na ścianę oddziaływuje bezpośrednio obciążenie poziome, wartość e wzrasta o mimośród dodatkowy e_m,w równy:

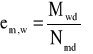
w którym:

M_wd - obliczeniowy moment zginający w połowie wysokości ściany, obliczony jak dla belki wolnopodpartej, w przypadku obciążenia równomiernie rozłożonego w_d

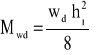
Wartość Φ_m wyznacza się w przypadku modelu przegubowego w sposób analogiczny jak dla modelu ciągłego (p. 5.1.2, dla e_m wyznaczonego ze wzoru (31) i - jeżeli zachodzi taka potrzeba - ze wzoru (32)).

Tablica 16 -Współczynnik redukcyjny nośności Φ_m

Współczynnik smukłości			Mimośród em
1000	700	400	0,05t	0,10t	0,15t	0,20t	0,25t	0,30t	0,33t
0	0	0	0,90	0,80	0,70	0,60	0,50	0,40	0,34
1	1	1	0,90	0,80	0,70	0,60	0,50	0,40	0,34
2	2	1,3	0,90	0,80	0,70	0,60	0,50	0,40	0,34
3	3	1,9	0,90	0,80	0,70	0,60	0,50	0,40	0,34
4	3,3	2,6	0,90	0,80	0,70	0,60	0,49	0,39	0,33
5	4,2	3,2	0,89	0,79	0,69	0,59	0,49	0,39	0,33
6	5,0	3,8	0,88	0,78	0,68	0,58	0,48	0,38	0,32
7	5,9	4,4	0,88	0,77	0,67	0,57	0,47	0,37	0,31
8	6,7	5,1	0,86	0,76	0,66	0,56	0,45	0,35	0,29
9	7,5	5,7	0,85	0,75	0,65	0,54	0,44	0,34	0,28
10	8,4	6,3	0,84	0,73	0,63	0,53	0,42	0,32	0,26
11	9,2	7,0	0,82	0,72	0,61	0,51	0,40	0,30	0,24
12	10,0	7,6	0,80	0,70	0,59	0,49	0,38	0,28	0,22
13	10,9	8,2	0,79	0,68	0,57	0,47	0,36	0,26	0,20
14	11,7	8,8	0,77	0,66	0,55	0,45	0,34	0,24	0,18
15	12,5	9,5	0,75	0,64	0,53	0,42	0,32	0,22	0,16
16	13,4	10,1	0,72	0,61	0,51	0,40	0,30	0,20	0,15
17	14,2	10,7	0,70	0,59	0,48	0,38	0,28	0,18	0,13
18	15,0	11,3	0,68	0,57	0,46	0,35	0,25	0,16	0,11
19	15,9	12,0	0,65	0,54	0,44	0,33	0,23	0,14	0,10
20	16,7	12,6	0,63	0,52	0,41	0,31	0,21	0,13	0,08
21	17,6	13,3	0,60	0,49	0,39	0,29	0,19	0,11	0,07
22	18,4	13,9	0,58	0,47	0,36	0,26	0,17	0,10	0,06
23	19,2	14,6	0,55	0,44	0,34	0,24	0,16	0,08	0,05
24	20,0	15,2	0,52	0,42	0,32	0,22	0,14	0,07	0,04
25	20,9	15,8	0,50	0,39	0,29	0,20	0,12	0,06	0,04
26	21,7	16,4	0,47	0,37	0,27	0,18	0,11	0,05	0,03
27	22,6	17,1	0,45	0,35	0,25	0,17	0,10	0,04	0,02
28	23,4	17,7	0,42	0,32	0,23	0,15	0,08	0,04	0,02
29	24,3	18,3	0,40	0,30	0,21	0,13	0,07	0,03	0,01
30	25,0	19,0	0,37	0,28	0,19	0,12	0,06	0,03	0,01

5.1.5 Ściana poddana obciążeniu skupionemu

Jeżeli ściana wykonana z elementów murowych grupy 1 i spełniająca wymagania konstrukcyjne podane w rozdziale 5 poddana jest obciążeniu skupionemu, należy sprawdzić, czy lokalne średnie naprężenie ściskające pod obliczeniowym obciążeniem skupionym, określone wzorem:

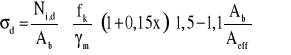
(39)

spełnia następujące warunki:

(40)

oraz:

• kiedy x = 0
  

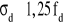
• kiedy x = 1,0
  

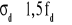
• kiedy 0 < x < 1,0 wartości górnego ograniczenia ustala się przez interpolację                                 liniową między 1,25 f_d i 1,5 f_d

w których:

f_d - obliczeniowa wytrzymałość muru na ściskanie,

x = 2a₁/H, lecz nie więcej niż 1,0;

a₁ - odległość od krawędzi ściany do najbliższej krawędzi pola oddziaływania       obciążenia skupionego (patrz rysunek 7);

H - wysokość ściany do poziomu obciążenia;

A_b - pole oddziaływania obciążenia skupionego, nie większe jednak niż 0,45 A_eff;

A_eff - efektywne pole przekroju o wymiarach L_eff × t (rys. 7)

L_eff - efektywna długość określona w połowie wysokości ściany lub przypory

        (rys. 7)

N_i,d - obliczeniowe obciążenie skupione

Rysunek 7 - Ściana poddana obciążeniu skupionemu

W przypadku ścian wykonanych z elementów murowych grupy 2 i 3, lokalne obliczeniowe naprężenia ściskające nie może być większe niż f_d. Kiedy bezpośrednio pod obciążeniem skupionym w ścianie wykonana została warstwa muru z elementów murowych grupy 1, można przyjąć, że obciążenie skupione rozkłada się pod katem 60° jak na rys. 7.

Zaleca się, aby wypadkowa naprężeń
znajdowała się w stosunku do płaszczyzny ściany w odległości nie większej niż 0,25 t.

Poza sprawdzeniem nośności ściany pod obciążeniem skupionym, należy również sprawdzić „klasyczną” nośność ściany wg zasad wcześniej podanych.

16

---