SPRAWOZDANIE Z LABORATORIUM Techniki Analogowej
Wykonał:	Nr grupy lab.:	Termin:	Data wyk. ćw.
Prowadzący:
Ćwiczenie nr 8 Własności funkcji transmitancji			Ocena

Cel ćwiczenia:

Celem ćwiczenia jest zbadanie wpływu zmian położenia biegunów funkcji transmitancji układu na jego odpowiedź impulsową oraz na jego charakterystykę częstotliwościową.

W ćwiczeniu należy wyznaczyć odpowiedź impulsową układu realizującego:

• pojedynczy biegun na osi rzeczywistej w lewej półpłaszczyźnie zmiennej s,

• parę biegunów na osi rzeczywistej w lewej półpłaszczyźnie zmiennej s,

• parę biegunów zespolonych sprzężonych w lewej półpłaszczyźnie zmiennej s.

Transmitancja układu ma postać:

.

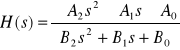
Przebieg ćwiczenia:

Pomiary wykonałem w układzie przedstawionym na rys.2.

Rys. 2. Schemat układu pomiarowego

Układ był pobudzany impulsem prostokątnym o parametrach:

• czas trwania impulsu: τ = 7 μs

• amplituda impulsu: A = 8 V

Pole impulsu pobudzającego

1. Badanie odpowiedzi układu I rzędu

a)Znormalizowany biegun funkcji transmitancji s₀=-0.2:

Do badania odpowiedzi układu pierwszego rzędu przyjęto parametry:

A₂ = 0; A₁ = 0.31; A₀ = 0.94; B₂ = 0.31; B₁ = 1; B₀ = 0.19;

Funkcja transmitancji ma postać:

.

Transmitancja H(s) jest wielkością znormalizowaną. Częstotliwość normalizująca wynosi:

f₀ = 1 [kHz],

zatem stosując podstawienie:

,gdzie p- zdenormalizowany biegun transmitancji.

Funkcja transmitancji ma postać:

.

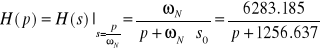
Odpowiedź impulsowa układu (wykres nr 1) :

.

b) Znormalizowany biegun funkcji transmitancji s₀=-0.6:

Do badania odpowiedzi układu pierwszego rzędu przyjęto parametry:

A₂ = 0 ; A₁ = 0.28 ; A₀ = 0.83 ; B₂ = 0.28 ; B₁ = 1 ; B₀ = 0.5;

Funkcja transmitancji ma postać:

.

Funkcja zdenormalizowana :

.

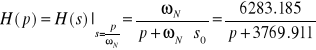
Odpowiedź impulsowa układu (wykres nr 2) :

.

2. Badanie odpowiedzi układu II rzędu

a) Dwa różne znormalizowane bieguny rzeczywiste

Do badania odpowiedzi układu drugiego rzędu przyjęto parametry:

A₂ = A₁= 0 ; A₀ =1 ; B₂ = B₁= 1 ; B₀ = 0.24

Dla takich parametrów funkcja transmitancji przyjmuje postać:

.

Denormalizując funkcję transmitancji otrzymamy:

.

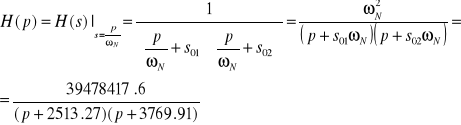
Odpowiedź impulsowa układu (wykres nr 3) :

.

b) Podwójny znormalizowany biegun rzeczywisty

Do badania odpowiedzi układu drugiego rzędu przyjęto parametry:

A₂ = A₁= 0 ; A₀ = 1 ; B₂ = B₁= 1 ; B₀ = 0.25.

Funkcja transmitancji ma postać:

.

Denormalizując funkcję transmitancji otrzymamy:

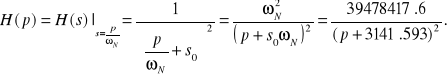
Odpowiedź impulsowa układu (wykres nr 4) :

.

3. Układ II rzędu (urojone znormalizowane bieguny transmitancji)

a) Układ bazowy:

Do badania odpowiedzi układu drugiego rzędu z pierwiastkami sprzężonymi przyjęto parametry:

A₂ = A₁= 0 ; A₀ = 1 ; B₂ = 1 ; B₁ = 0.4 ; B₀ = 0.2.

Dla takich parametrów funkcja transmitancji przyjmuje postać:

.

Znormalizowane pierwiastki funkcji transmitancji wynoszą:

;
.

Denormalizując funkcję transmitancji otrzymamy:

.

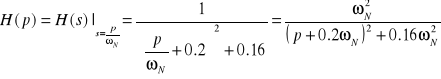
Odpowiedź impulsowa układu (wykres nr 5) :

.

,gdy
:

.

b) Pierwiastki zespolone sprzężone - zmiana części urojonej

Do badania odpowiedzi układu drugiego z pierwiastkami sprzężonymi rzędu przyjęto parametry:

A₂ = A₁= 0 ; A₀ = 1 ; B₂ = 1 ; B₁ = 0.4 ; B₀ = 0.68.

Dla takich parametrów funkcja transmitancji przyjmuje postać:

.

Znormalizowane pierwiastki funkcji transmitancji wynoszą:

;
.

Normalizując funkcję transmitancji otrzymamy:

.

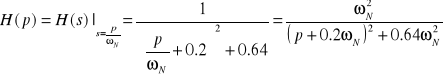
Funkcja transmitancji ma postać:

.

Odpowiedź impulsowa układu (wykres nr 6) :

.

c) Pierwiastki zespolone sprzężone - zmiana części rzeczywistej

Do badania odpowiedzi układu drugiego z pierwiastkami sprzężonymi rzędu przyjęto parametry:

A₂ = A₁= 0 ; A₀ = 1 ; B₂ = 1 ; B₁ = 0.8 ; B₀ = 0.32

Dla takich parametrów funkcja transmitancji przyjmuje postać:

.

Znormalizowane pierwiastki funkcji transmitancji wynoszą:

;
.

Denormalizując funkcję transmitancji otrzymamy:

.

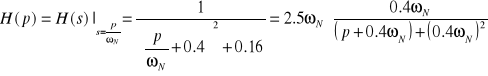
Podstawiając
, odpowiedź impulsowa układu (wykres nr 7) :

.

4. Charakterystyki amplitudowe:

a) Charakterystyka amplitudowa układu pierwszego rzędu (2a):

Dla parametrów z punktu 2a, teoretyczna charakterystyka amplitudowa ma postać :

.

Wyniki pomiarów dla układu pierwszego rzędu (wykres nr 8) :

f [Hz]	U [V]
20	3.52
50	3.53
100	3.45
125	3.39
150	3.32
175	3.24
200	3.15
225	3.06
250	2.96
275	2.85
300	2.74
350	2.53
400	2.33
450	2.13
500	1.92
600	1.6
700	1.31
800	1.11
900	0.92
1000	0.78
1100	0.68
1200	0.58
1300	0.51
1400	0.43
1500	0.39
1600	0.33
1700	0.3
1800	0.27
1900	0.24
2000	0.22
2200	0.18
2400	0.14
2500	0.13
2600	0.12
2700	0.1
3000	0.09

b) Charakterystyka amplitudowa układu drugiego rzędu (3b):

Wyniki pomiarów dla parametrów z punktu 3b (wykres nr 9):

f [Hz]	U [V]
20	1.36
30	1.39
60	1.42
100	1.42
150	1.45
200	1.47
250	1.51
300	1.58
350	1.64
400	1.73
450	1.82
500	1.94
525	2
550	2.1
575	2.12
600	2.23
650	2.38
700	2.53
800	2.63
825	2.61
850	2.53
875	2.45
900	2.34
950	2.08
1000	1.8
1100	1.39
1200	1.12
1250	0.96
1300	0.85
1350	0.78
1400	0.7
1500	0.58
1550	0.52
1600	0.47
1700	0.41
1800	0.36
1900	0.3
2000	0.26
2100	0.24
2200	0.21
2300	0.19
2400	0.17
2500	0.14
2600	0.14
2700	0.13

5. Wnioski:

Dla pojedynczego bieguna rzeczywistego odpowiedzią układu na pobudzenie impulsowe jest funkcja ekspotencjalnie malejąca.Szybkość tłumienia funkcji ekspotencjalnej zależy od położenia biegunów. Im biegun jest bardziej oddalony od osi OY w lewą stronę, tym sygnał jest bardziej tłumiony, czyli występuje większa szybkość opadania odpowiedzi. Analizując charakterystykę obliczyłem rzeczywiste wartości biegunów funkcji. Różnice w stosunku do założonych wartości mogą wynikać z błędów podczas ustawiania parametrów A₂…, B₂….B₀, oraz z błędów odczytu z charakterystyk.

Wyznaczając odpowiedź układu drugiego rzędu o podwójnym biegunie s0 = -0,5 możemy powiedzieć, iż jej charakter - początkowo narastający, a następnie powyżej opadający do zera - jest typową odpowiedzią dla układów o rzeczywistych biegunach podwójnych. W zależności od położenie tego bieguna w lewej półpłaszczyźnie odpowiedź może zmieniać swoje parametry, lecz nie zmieni się jej charakter.

Obserwacja odpowiedzi impulsowej dla układu drugiego rzędu o biegunach zespolonych pozwala nam stwierdzić, iż w przypadku biegunów położonych w lewej półpłaszczyźnie układu współrzędnych odpowiedzi mają charakter oscylacyjny gasnący. Możemy stwierdzić, że im większa wartość współczynnika
- część rzeczywista bieguna - tym odpowiedź szybciej osiąga wartość zero. Z kolei im większa wartość
- część urojona bieguna - tym mniejszy okres oscylacji.

Pierwszą charakterystykę amplitudową wyznaczono dla biegunów:

s1=-0,4; s2=-0,6. Jej kształt jest zgodny z przewidywaniami. Powyżej f = 100Hz charakterystyka opada, co prawdopodobnie świadczy o dużym tłumieniu układu dla wyższych częstotliwości.

Druga charakterystyka amplitudowa dla biegunów s₁=-0,2+j0,8; s₂=-0,2-j0,8,charakteryzuje się wzmocnieniem dla częstotliwości f=800Hz. Dla częstotliwości większej od f=1000Hz układ ma charakter tłumiący.

Wykres nr 8 : Charakterystyka amplitudowa układu pierwszego rzędu:

Wykres nr 9: Charakterystyka amplitudowa układu drugiego rzędu:

---