RÓWNANIA RÓŻNICZKOWE

§1 Równania różniczkowe rzędu I

§2 Równania różniczkowe rzędu II

§3 Równania różniczkowe rzędu III

§1 Równania różniczkowe rzędu I

1.WIADOMOŚCI OGÓLNE

Równanie postaci f(x, y, y')=0, w którym istotnie występuje pochodna y' szukanej funkcji y(x) nosi nazwę RÓWNANIA RÓŻNICZKOWEGO I-go RZĘDU .

np.
.

Rozwiązać równanie różniczkowe tzn. znaleźć taką funkcję y =
(x), która równanie przekształca w tożsamość.

Najprostszymi równaniami różniczkowymi rzędu I są RÓWNANIA NORMALNE postaci:

1. 
   .

Tego typu równania można rozwiązać przez kwadratury, czyli przez całkowanie. Wtedy rozwiązanie równania (1) postaci

2. 
   

jest zależne od stałej i będzie nosić nazwę CAŁKI OGÓLNEJ.

W interpretacji geometrycznej całka ogólna jest jednoparametrową rodziną krzywych całkowych.

ZAGADNIENIE CAUCHY'EGO

Zagadnienie Cauchy'ego dla równania (1) polega na znalezieniu takiego rozwiązania tzn. takiej całki szczególnej tego równania, które spełnia warunek początkowy:
, gdzie
,
są danymi liczbami. Wówczas wstawiając do całki ogólnej (2) wartości
,
otrzymujemy równość, z której obliczamy c:
.

W ten sposób

3. 
   
   

jest całką szczególną będącą rozwiązaniem zagadnienia Cauchy'ego dla równania (1).

W interpretacji geometrycznej zagadnienie Cauchy'ego dla równania (1) z warunkiem y(x0)=y0 polega na wybraniu spośród krzywych całkowych (2) takiej, która przechodzi przez z góry ustalony punkt P0(x0, y0).

2. RÓWNANIA RÓŻNICZKOWE O ZMIENNYCH ROZDZIELONYCH

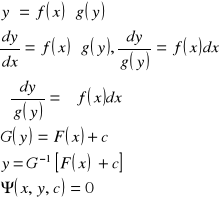
Przykład 1

Otrzymaliśmy całkę ogólną rozważanego równania. Aby rozwiązać zagadnienie Cauchy'ego stałą c obliczamy z narzuconych warunków początkowych:

3.RÓWNANIA RÓŻNICZKOWE JEDNORODNE POSTACI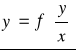
.

Aby rozwiązać tego typu równanie różniczkowe korzystamy z podstawienia:

Przykład 2

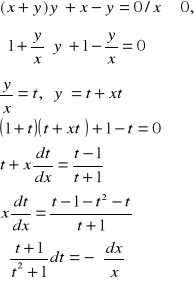
4.RÓWNANIA LINIOWE

1. y'+ p(x)y= f(x) - równanie liniowe niejednorodne (r.l.n.)

2. y'+ p(x)y= 0 - równanie liniowe jednorodne (f(x)≡0)

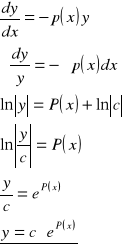
całka ogólna równania liniowego jednorodnego (c.o.r.l.j)

Całkę ogólną równania liniowego niejednorodnego poszukujemy metodą uzmiennienia stałej w postaci

Przykład 3

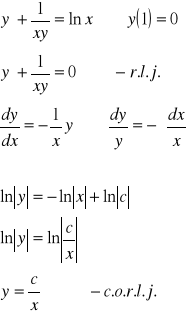
Stosujemy metodę uzmiennienia stałej poszukując rozwiązania w postaci

:

Aby z tej klasy rozwiązań wybrać jedno, spełniające warunek
należy wstawić za x=1 y=0.

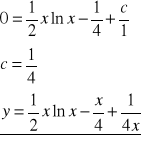
całka szczególna równania liniowego niejednorodnego (zagadnienie Cauchy'ego) spełniająca warunek

5. RÓWNANIE BERNOULLIEGO

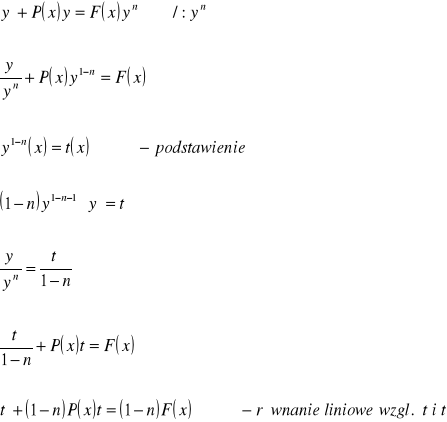
Przykład 4

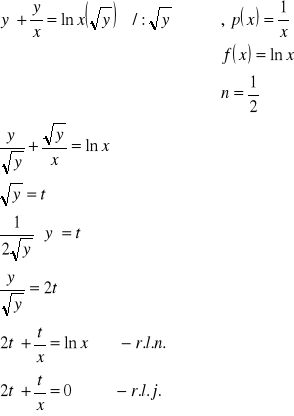
c.o.r.l.u. poszukujemy metodą uzmiennienia stałej:

Całka ogólna równania Bernoulliego:

§2. RÓWNANIA RÓŻNICZKOWE RZĘDU II.

1. WIADOMOŚCI WSTĘPNE

Równaniem różniczkowym rzędu II nazywamy związek postaci:

1. 
   ,

w którym istotnie występuje
szukanej funkcji
.

Dowolną funkcję

2. 
   

spełniającą ten związek nazywamy całką szczególną równania (1) (c.s.r.).

Najczęściej rozpatrywaną klasą równań typu (1) są równania postaci:

3. 
   

zwane równaniami normalnymi.

Zagadnienie początkowe (Cauchy'ego) dla równania (3) polega na znalezieniu takiej całki szczególnej tego równania, która spełnia warunki:

i
,

gdzie
to dane liczby.

Aby je rozwiązać należy określić całkę ogólną tego równania, która jest opisana funkcją:

4. 
   

określającą dwuparametrową rodzinę krzywych całkowych, spełniającą równanie (3).

Wtedy stałe
określamy ze wzorów (∗), tzn. z układu równań:

Jeżeli
i
są rozwiązaniem powyższego układu równań, to całka ogólna (4) przyjmuje postać:

5. 
   

i jest rozwiązaniem powyższego zagadnienia Cauchy'ego.

Podobnie, zagadnienie brzegowe dla równania (3) polega na wyborze spośród krzywych całkowych (4) takiej, która przechodzi przez z góry ustalone punkty
i
.

Wtedy parametry
obliczamy z układu równań:

2. RÓWNANIA RÓŻNICZKOWE RZĘDU II-go SPROWADZALNE DO RÓWNAŃ RZĘDU I-go

1° Równanie różniczkowe II-go rzędu postaci y''=f(x)

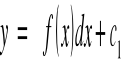
2º Równanie różniczkowe II-go rzędu bez szukanej funkcji podanej w sposób jawny:

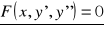
- równanie różniczkowe rzędu I-go

3º Równanie różniczkowe II-go rzędu bez zmiennej niezależnej podanej w sposób jawny:

Przykład 1

Rozwiązać zagadnienie brzegowe:

dla równania

całka ogólna

Aby określić krzywą całkową musimy rozwiązać układ równań:

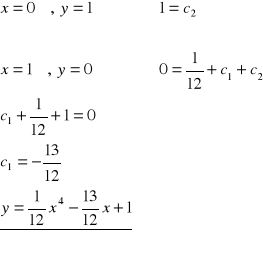
całka szczególna będąca rozwiązaniem rozważanego zagadnienia brzegowego.

Przykład 2

Warunki:

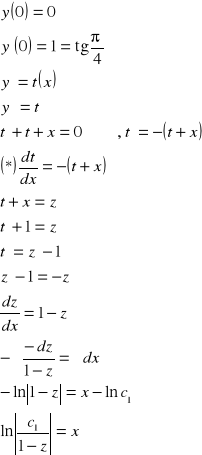
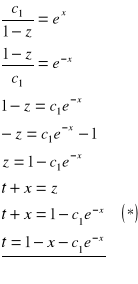
całka ogólna

całka ogólna równania rzędu II

całka szczególna będąca rozwiązaniem zagadnienia

Przykład 3

3.RÓWNANIA LINIOWE RZĘDU II-go:

Równaniem liniowym niejednorodnym rzędu II-go nazywamy równanie postaci:

Jeżeli
, to równanie liniowe nazywamy JEDNORODNYM i ma ono postać:

.

Dalsze ograniczenia dotyczą funkcji:
-stałe

Wtedy

jest równaniem liniowym rzędu II-go o współczynnikach stałych.

Całkę szczególną powyższego równania poszukujemy w postaci:
, gdzie r oznacza dobrany parametr.

Wstawiamy do równania (3):

Równanie (4) nazywamy równaniem charakterystycznym dla równania (3).

I

Całki szczególne liniowo niezależne tzn.

Wtedy

jest całka ogólną równania liniowego jednorodnego (równania

są liniowo niezależne)

.

II
-pierwiastek podwójny

-całki liniowo niezależne

Jeżeli coś jest całką ogólną, to po pomnożeniu przez x uzyskujemy również całkę ogólną.

Zatem

-całka ogólna

III

- pierwiastki sprzężone

- całka ogólna

bo
są liniowo niezależne.

↑ ↑

A B

-całka ogólna A,B - stałe

UWAGA!

Całki liniowo niezależne mają być przedstawione w postaci:

Można dowieść, że jeżeli
jest całką ogólną równania liniowego jednorodnego takiej postaci
i
- jest całką szczególną równania liniowego niejednorodnego
, to
jest całką ogólną równania liniowego niejednorodnego.

Uwaga 1

Własność powyższa dotyczy również przypadku, gdy p i q są funkcjami.

Uwaga 2

jest łatwo przewidzieć, gdy po prawej stronie są funkcje wielomianowe i wykładnicze:

Uwaga 3

Układ całek liniowo niezależnych
,
określających całkę ogólną równania liniowego jednorodnego za pomocą wzoru
jest łatwo określić w przypadku współczynników stałych.

Przykład 1

- równanie liniowe niejednorodne

- równanie liniowe jednorodne

↑

rząd pochodnej zmienia się w stopień r

↓

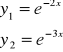
całki sprzężone liniowe niejednorodne, bo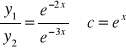
(iloraz nie jest stały, jest funkcją)

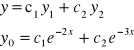
Całkę sprzężoną równania liniowego niejednorodnego przewidujemy w postaci podobnej do prawej strony
A, B tak dobrane, by
spełniało równanie liniowe niejednorodne.

→

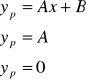
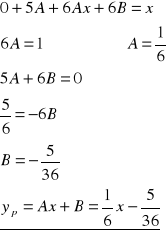
całka przewidywana

Wtedy
→ Całka ogólna równania liniowego niejednorodnego

Przykład 2

- równanie liniowe niejednorodne rzędu II

- y przewidywane

- równanie liniowe jednorodne

↓

- równanie charakterystyczne

całka ogólna równania liniowego jednorodnego

, A, B, a, b, k=?

↓

całka przewidywana równania liniowego niejednorodnego

Wstawiając powyższe do r.l.n. postaci

dostajemy

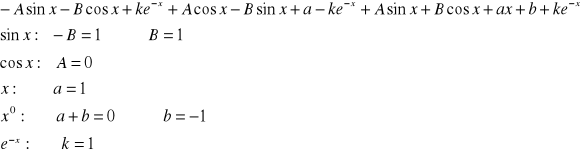
Zatem

- całka szczególna równania liniowego niejednorodnego

Wtedy

- całka ogólna równania liniowego niejednorodnego

- całka ogólna równania liniowego niejednorodnego

Aby określić całkę szczególną spełniającą warunki
należy rozwiązać układ:

Wstawiając
i
do równania liniowego ogólnego otrzymujemy całkę szczególną równania liniowego niejednorodnego spełniającą warunki początkowe. Oznacza to, że spośród dwuparametrowej rodziny krzywych całkowych wybraliśmy jedyną, która przechodzi przez początek układu (0,0) i której styczna w punkcie 0 jest nachylona pod kątem

do osi x.

Uwaga

Jeżeli podane są warunki początkowe w zerze tzn.:
,

to rozwiązanie zagadnienia Cauchy'ego można otrzymać za pomocą transformat Laplace'a:

- transformata odwrotna

Skorzystamy dalej z metody tranformacji Laplace'a

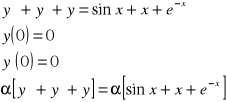
Ponieważ transformacja Laplace'a jest przekształceniem całkowym więc jest jednorodna i addytywna.

.

W celu znalezienia powyższych transformat skorzystamy z następujących ich własności :

Tablica transformat Laplace'a

0 0 0

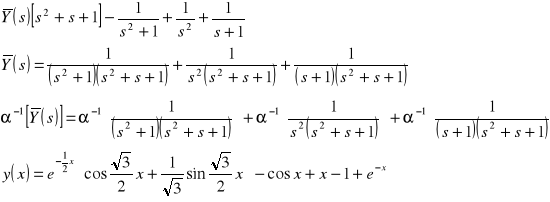
Uwaga 2

Gdy brak warunków początkowych stosujemy znaną metodę przewidywań, w przypadku prawej strony
będącej funkcją wielomianowo-wykładnikowo-trygonometryczną wtedy
, gdzie
, to całka ogólna równania liniowego jednorodnego, a
, to całka szczególna równania liniowego niejednorodnego.

Uwaga 3

W przypadku innym tzn. gdy
nie jest funkcją wykładniczo-wielomianowo-trygonometryczną stosujemy metodę uzmiennienia stałych. Polega ona na tym, że znając całkę ogólną równania liniowego jednorodnego w postaci:
(
,
- całki sprzężone równania liniowego jednorodnego liniowo zależne), całki ogólnej równania liniowego niejednorodnego poszukujemy w postaci

tzn.

Funkcje
i
należy tak więc dobrać, by (
) spełniało równanie liniowe niejednorodne. Można dowieść, że
i
należy obliczyć z układu równań:

Agnieszka Szablewska i Magdalena Skrzypczak

0

l

x

y

1

P₀ (x₀,y₀)

x

y

1

x

y