Do wykresu jednomianu kwadratowego należy punkt ![]()
. Wzór tego jednomianu ma postać
a) |
b) |
c) |
d) |
Aby otrzymać wykres funkcji
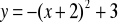
należy o pewien wektor przesunąć wykres jednomianu kwadratowegoAby otrzymać wykres funkcji
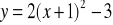
należy przesunąć wykres pewnego jednomianu kwadratowego o wektorPrzesuwając wykres funkcji
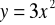
o wektor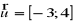
otrzymamy wykres funkcjiDana jest funkcja kwadratowa
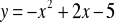
. Postać kanoniczna tej funkcji toDana jest funkcja kwadratowa
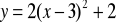
.Postać ogólna tej funkcji to
Wierzchołek paraboli będącej wykresem tej funkcji to punkt
Funkcja kwadratowa
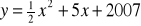
Dana jest funkcja kwadratowa
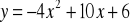
. Postać iloczynowa tej funkcji toDana jest funkcja kwadratowa
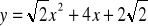
. Postać iloczynowa tej funkcji toWiadomo że
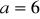
, oraz miejscami zerowymi funkcji kwadratowej są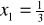
i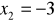
.Dana jest funkcja kwadratowa
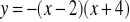
. Postać ogólna tej funkcji toDana jest funkcja
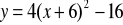
. Postać iloczynowa tej funkcji toDana jest funkcja
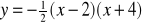
. Postać kanoniczna tej funkcji toDana jest funkcja
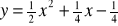
. Miejscami zerowymi tej funkcji sąDana jest funkcja
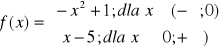
.Funkcja ta
W przedziale
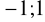
funkcja taW przedziale
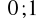
funkcja taWiadomo że miejscami zerowymi trójmianu kwadratowego są
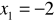
i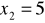
. Ponadto wykres przechodzi przez punkt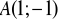
. Funkcja ta określona jest wzoremDo wykresu funkcji
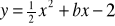
należy punkt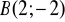
. Wobec tegoZbiorem wartości funkcji
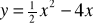
jest przedziałDo wykresu trójmianu kwadratowego
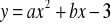
należy punkt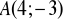
i jednym z miejsc zerowych trójmianu jest liczba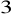
. Wzór tej funkcji ma postaćJedynym miejscem zerowym funkcji kwadratowej jest liczba
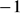
. Ponadto wykres przechodzi przez punkt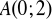
. Funkcja ta określona jest wzoremFunkcja
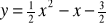
Ma w przedziale
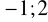
wartość największą równąMa w przedziale
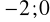
wartość najmniejszą równąNiech
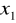
,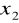
oznaczają miejsca zerowe trójmianu kwadratowego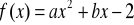
. Ponadto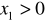
i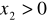
. Wobec tegoNiech
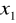
,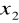
oznaczają miejsca zerowe trójmianu kwadratowego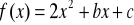
. Ponadto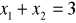
i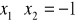
. Funkcja ta określona jest wzoremZbiorem wszystkich rozwiązań równania kwadratowego
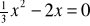
jestZbiorem wszystkich rozwiązań równania kwadratowego
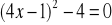
jestRównanie
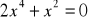
Zbiorem wszystkich rozwiązań równania
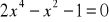
jestZbiorem wszystkich rozwiązań nierówności
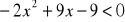
jest
a) |
b) |
c) |
d) |
a) |
b) |
c) |
d) |
a) |
b) |
c) |
d) |
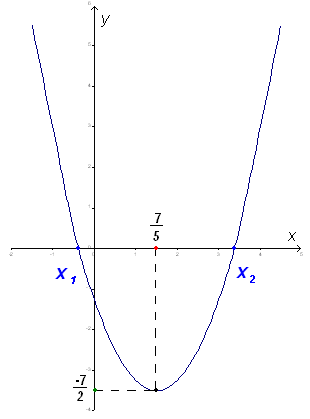
Przedstawiony wykres funkcji otrzymano w wyniku przesunięcia wykresu
jednomianu kwadratowego ![]()
o pewien wektor. Wzór tej funkcji ma postać
a) |
b) |
c) |
d) |
a) |
b) |
c) |
d) |
|
|
|
|
a) |
b) |
c) |
d) |
a) |
b) |
c) |
d) |
a) nie ma miejsc zerowych |
b) ma jedno miejsce zerowe |
c) ma dwa miejsca zerowe |
a) |
b) |
c) |
d) |
a) |
b) |
c) |
d) |
Postać iloczynowa tej funkcji to
a) |
b) |
c) |
d) |
a) |
b) |
c) |
d) |
a) |
b) |
c) |
d) |
a) |
b) |
c) |
d) |
a) |
b) |
c) |
d) |
a) nie ma miejsc zerowych |
b) ma dokładnie jedno miejsce zerowe |
c) ma dokładnie dwa miejsca zerowe |
d) ma dokładnie trzy miejsce zerowe |
a) jest stała |
b) jest rosnąca |
c) jest malejąca |
d) nie jest monotoniczna |
a) przyjmuje wartości nieujemne |
b) przyjmuje tylko wartości ujemne |
c) ma miejsce zerowe |
a) |
b) |
c) |
d) |
a) |
b) |
c) |
d) |
a) |
b) |
c) |
d) |
a) |
b) |
c) |
d) |
a) |
b) |
c) |
d) |
a) |
b) |
c) |
d) |
a) |
b) |
c) |
d) |
a) |
b) |
c) |
d) |
|
|
|
|
a) |
b) |
c) |
d) |
a) |
b) |
c) |
d) |
a) |
b) |
c) |
d) |
a) ma dokładnie jedno rozwiązanie |
b) ma dokładnie dwa rozwiązania |
c) ma dokładnie trzy rozwiązania |
d) ma dokładnie cztery rozwiązania |
a) |
b) |
c) |
d) |
a) |
b) |
c) |
d) |