Akademia Górniczo Hutnicza w Krakowie
LABORATORIUM Z PODSTAW AUTOMATYKI
TEMAT ĆWICZENIA: Rozwiązywanie równań różniczkowych z niezerowymi warunkami początkowymi
MSE Rok 3 grupa 3	Data wykonania 10-01-2007 r.		Data zaliczenia	Ocena	Tomasz Siwek

1. Cel ćwiczenia:

• zapoznanie się z różnymi metodami rozwiązywania równań różniczkowych w Matlabie,

• wykorzystanie Simulinka do tworzenia modelu równania różniczkowego,

• archiwizacja otrzymanych rozwiązań,

2. Przebieg ćwiczenia:

2.1 Rozwiązać równania różniczkowe wykorzystując funkcje ode45 oraz model równania przygotowany w Simulinku. Wykreślić przebieg funkcji y(t) otrzymanej w wyniku symulacji i porównać wyniki otrzymane w obu metodach.

a.)
dla war. początkowych: y(0)=0 i y'(0)=0

• przekształcamy powyższe równanie do postaci równań stanu:

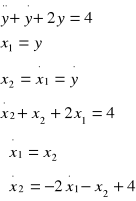
• tworzymy m-plik definiujący równania stanu:

function xdot=funkcja1a(t,x)

% Układ rownan rozniczkowych

xdot=zeros(2,1);

xdot(1)=x(2);

xdot(2)=(-2*x(1)-1*x(2)+4);

• wprowadzamy parametry wejściowe i wywołujemy funkcje ode45:

function rozw1a

t0=0;

clc

disp('Funkcja rozwiazuje rownanie rozniczkowe zwyczajne metodą ');

disp('Rungego - Kutty i podaje jego interpretacje graficzna:');

disp(' ');disp('Postac rownania:');disp(' ');

disp(' y``+ y`+ 2y = 4');

disp(' warunki początkowe:');

y01=0

y02=0

tk=input ('Podaj czas symulacji tk = ');

% przyjąłem tk=10

y0=[y01 y02];

[t,x]=ode45('funkcja1a',t0,tk,y0,0.001,0);

plot(t,x(:,1),'r-');

xlabel('czas [s]');ylabel('amplituda sygnalu');

title('Wykres rozwiazania rownania rozniczkowego y``+ y`+ 2y = 4');

grid;

• w wyniku wywołania powyższego m-pliku otrzymujemy wykres który jest rozwiązaniem pierwszego równania:

• 
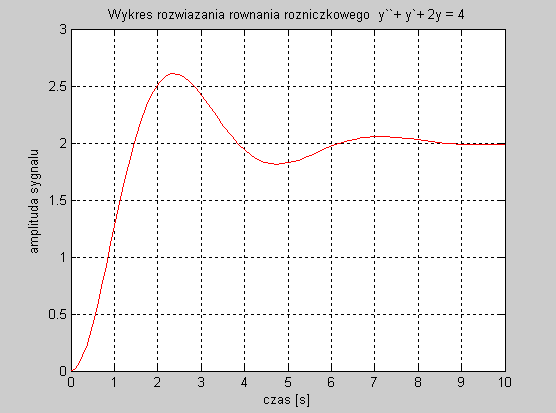
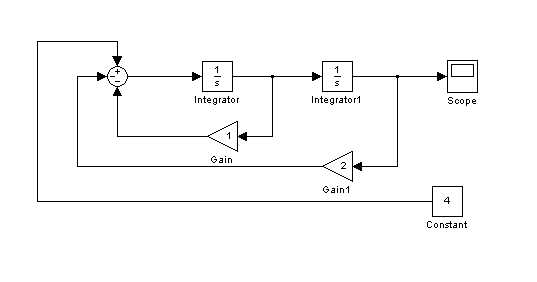
  To samo równanie różniczkowe rozwiązujemy przy pomocy Simulinka. W pierwszym kroku budujemy układ.

• W wyniku symulacji otrzymujemy następujący przebieg:

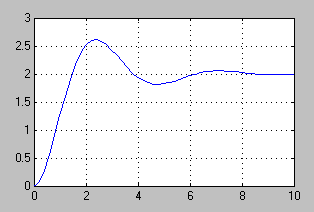
b.)
dla war. początkowych: y(0)=1 i y'(0)=1

• Z drugim równaniem postępujemy analogicznie, przekształcamy powyższe równanie do postaci równań stanu:

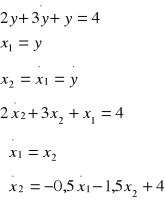
• tworzymy m-plik definiujący równania stanu:

function xdot=funkcja1b(t,x)

% Układ rownan rozniczkowych

xdot=zeros(2,1);

xdot(1)=x(2);

xdot(2)=(-0.5*x(1)-1.5*x(2)+4);

• wprowadzamy parametry wejściowe i wywołujemy funkcje ode45:

function rozw1b

t0=0;

clc

disp('Funkcja rozwiazuje rownanie rozniczkowe zwyczajne metodą ');

disp('Rungego - Kutty i podaje jego interpretacje graficzna:');

disp(' ');disp('Postac rownania:');disp(' ');

disp(' 2y``+ 3y`+ y = 4');

disp(' warunki początkowe:');

y01=1

y02=1

tk=input ('Podaj czas symulacji tk = ');

y0=[y01 y02];

[t,x]=ode45('funkcja1b',t0,tk,y0,0.001,0);

plot(t,x(:,1),'r-');

xlabel('czas [s]');ylabel('amplituda sygnalu');

title('Wykres rozwiazania rownania rozniczkowego 2y``+ 3y`+ y = 4');

grid;

• w wyniku wywołania powyższego m-pliku otrzymujemy wykres który jest rozwiązaniem drugiego równania:

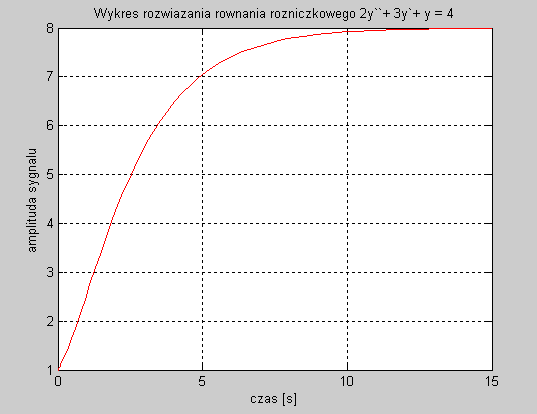
• To samo równanie różniczkowe rozwiązujemy przy pomocy Simulinka. W pierwszym kroku budujemy układ.

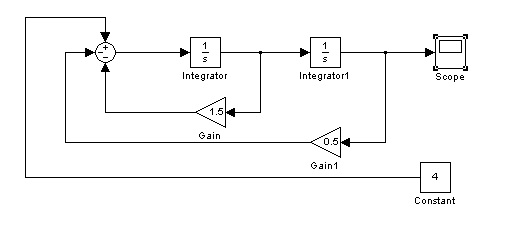
• W wyniku symulacji otrzymujemy następujący przebieg:

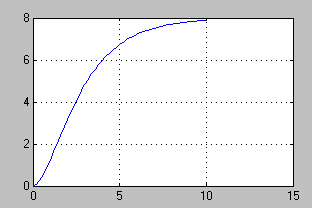
2.2 Skonstruować w Simulinku modele równań różniczkowych:

a.)
dla war. początkowych: y(0)=0 i y'(0)=0

• transmitancja powyższego równania i równania stanu mają następującą postać:

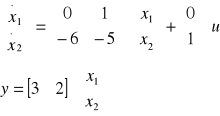
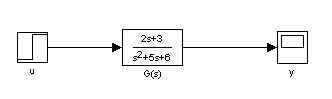
• równaniu a.) odpowiada następujący schemat blokowy zbudowany w oparciu
  o transmitancje i wykres uzyskany w wyniku symulacji:

• 
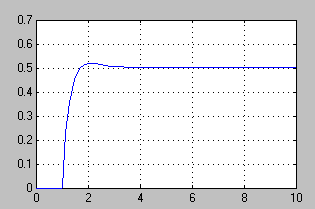
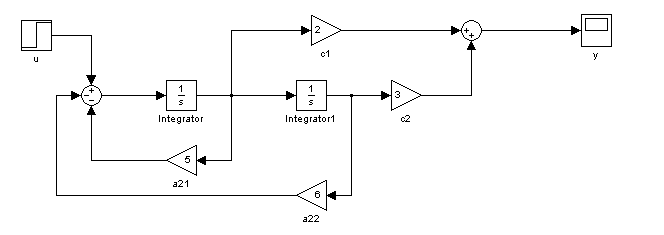
  kolejny schemat blokowy tworzymy w oparciu o równania stanu, w wyniku symulacji otrzymujemy następujący przebieg:

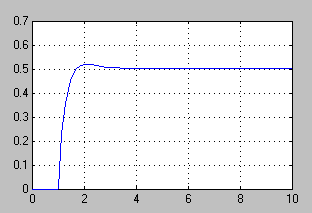
b.)
dla war. początkowych: y(0)=0 i y'(0)=0

• transmitancja powyższego równania i równania stanu mają następującą postać:

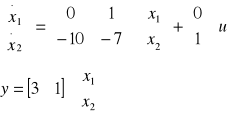
• równaniu b.) odpowiada następujący schemat blokowy zbudowany w oparciu
  o transmitancje i wykres uzyskany w wyniku symulacji:

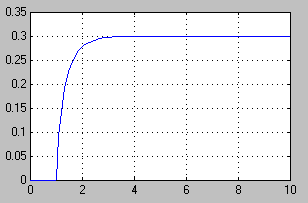
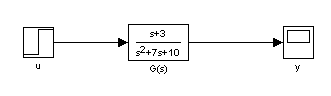
• kolejny schemat blokowy tworzymy w oparciu o równania stanu, w wyniku symulacji otrzymujemy następujący przebieg:

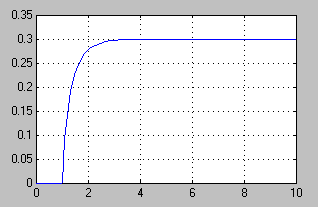
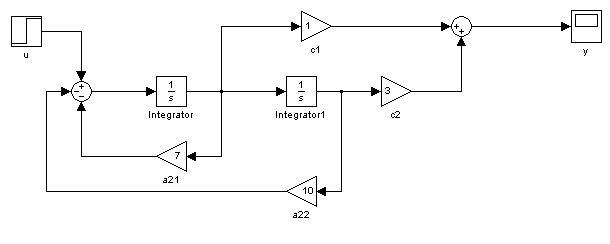
2.3 Rozwiązać równania różniczkowe wykorzystując funkcje ode45 i porównać
z rozwiązaniami analitycznym.

a.)
dla war. początkowych: y(0)=0 i y'(0)=15

• równania stanu przyjmują następującą postać:

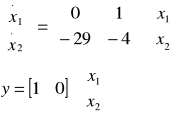
• rozwiązaniem analitycznym przedmiotowego równanie jest następująca funkcja:

• w oparciu o równania stanu definiujemy m-funkcje w Matlabie:

function xdot=funkcja4a(t,x)

% Układ rownan rozniczkowych

xdot=zeros(2,1);

xdot(1)=x(2);

xdot(2)=(-29*x(1)-4*x(2));

• wywołujemy m-plik porównujący rozwiązanie w oparciu o funkcje ode45
  i rozwiązanie analityczne:

function rozw4asum

t0=0;

clc

disp('Funkcja rozwiazuje rownanie rozniczkowe zwyczajne metodą ');

disp('Rungego - Kutty i podaje jego interpretacje graficzna:');

disp(' ORAZ ');

disp('Rysuje wykres rozwiązania analitycznego zadanego równania ');

disp(' Równanie : y``+ 4y`+ 29y = 0 ');

disp(' Rozwiązanie: y = 3*(e^(-2*t))*sin(5*t) ');

%ode45

disp(' warunki początkowe:');

x01=0

x02=15

tk=input ('Podaj czas symulacji tk = ');

x0=[x01 x02];

[t,x]=ode45('funkcja4a',t0,tk,x0,0.001,0);

plot(t,x(:,1),'r*');

xlabel('czas [s]');ylabel('amplituda sygnalu');

title('Wykres rozwiazania rownania rozniczkowego y``+ 4y`+ 29y = 0');

grid;

%rozwiązanie analityczne

t0a=0;ta=t0a:0.001:tk;

ya=3.*(exp((-2).*ta)).*(sin(5.*ta));

hold on

plot(ta,ya,'b-');

legend('ode45','analitycznie');

• w wyniku wywołania powyższego m-pliku otrzymujemy następujący wykres:

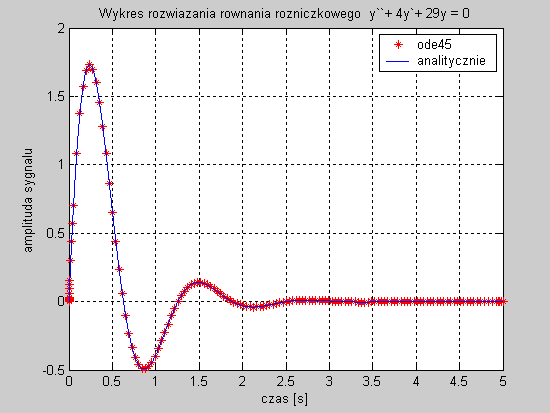
b.)
dla war. początkowych: y(0)=0 i y'(0)=9

• równania stanu przyjmują następującą postać:

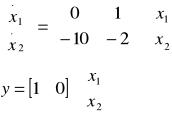
• rozwiązaniem analitycznym przedmiotowego równanie jest następująca funkcja:

• w oparciu o równania stanu definiujemy m-funkcje w Matlabie:

function xdot=funkcja4b(t,x)

% Układ rownan rozniczkowych

xdot=zeros(2,1);

xdot(1)=x(2);

xdot(2)=(-10*x(1)-2*x(2));

• wywołujemy m-plik porównujący rozwiązanie w oparciu o funkcje ode45
  i rozwiązanie analityczne:

function rozw4bsum

t0=0;

clc

disp('Funkcja rozwiazuje rownanie rozniczkowe zwyczajne metodą ');

disp('Rungego - Kutty i podaje jego interpretacje graficzna:');

disp(' ORAZ ');

disp('Rysuje wykres rozwiązania analitycznego zadanego równania ');

disp(' Równanie : y``+ 2y`+ 10y = 0 ');

disp(' Rozwiązanie: y = 3*(e^(-1*t))*sin(3*t) ');

%ode45

disp(' warunki początkowe:');

x01=0

x02=9

tk=input ('Podaj czas symulacji tk = ');

x0=[x01 x02];

[t,x]=ode45('funkcja4b',t0,tk,x0,0.001,0);

plot(t,x(:,1),'r*');

xlabel('czas [s]');ylabel('amplituda sygnalu');

title('Wykres rozwiazania rownania rozniczkowego y``+ 2y`+ 10y = 0');

grid;

%rozwiązanie analityczne

t0a=0;ta=t0a:0.001:tk;

ya=3.*(exp((-1).*ta)).*(sin(3.*ta));

hold on

plot(ta,ya,'b-');

legend('ode45','analitycznie');

• w wyniku wywołania powyższego m-pliku otrzymujemy następujący wykres:

3.Wnioski:

Na podstawie przeprowadzonych symulacji możemy stwierdzić, że dla danego równania każda z metod daje identyczne rozwiązanie graficzne. Teoretycznie jednak metoda analityczna jest najdokładniejsza bowiem daje rzeczywisty wynik, pozostałe metody są metodami numerycznymi i dają wyniki obarczone pewnym błędem, zależnym od kroku całkowania.

1

---