Magnetyczne właściwości cząsteczek
Pole magnetyczne o natężeniu H wywołuje w substancji indukcję magnetyczną B, której wielkość zależy od przenikalności magnetycznej κ.
![]()
Przenikalność magnetyczna próżni κ0=4π.10-7 (V.s)/(A.m)
Przenikalność magnetyczną substancji wyraża się względem różni κ/κ0 <1.
Względna przenikalność magnetyczna substancji zależy od właściwości substancji, czyli podatności magnetycznej χ, która zależy od:
trwałego momentu magnetycznego m,
magnetyzowalności substancji ξ
![]()
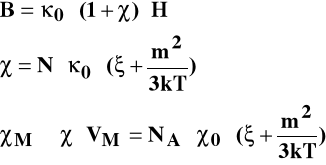
Paramagnetyki - składniki, których cząsteczki mają trwały moment magnetyczny, m≠0. Podatność magnetyczna paramagnetyków przyjmuje wartości dodatnie χ>0. Kierunek namagnesowania jest zgodny z kierunkiem pola magnetycznego.
Diamagnetyki - składniki, których cząsteczki nie mają trwałego momentu magnetycznego, m=0. Podatność magnetyczna diamagnetyków przyjmuje wartości ujemne χ<0. Kierunek namagnesowania jest przeciwny do kierunku działania pola magnetycznego.
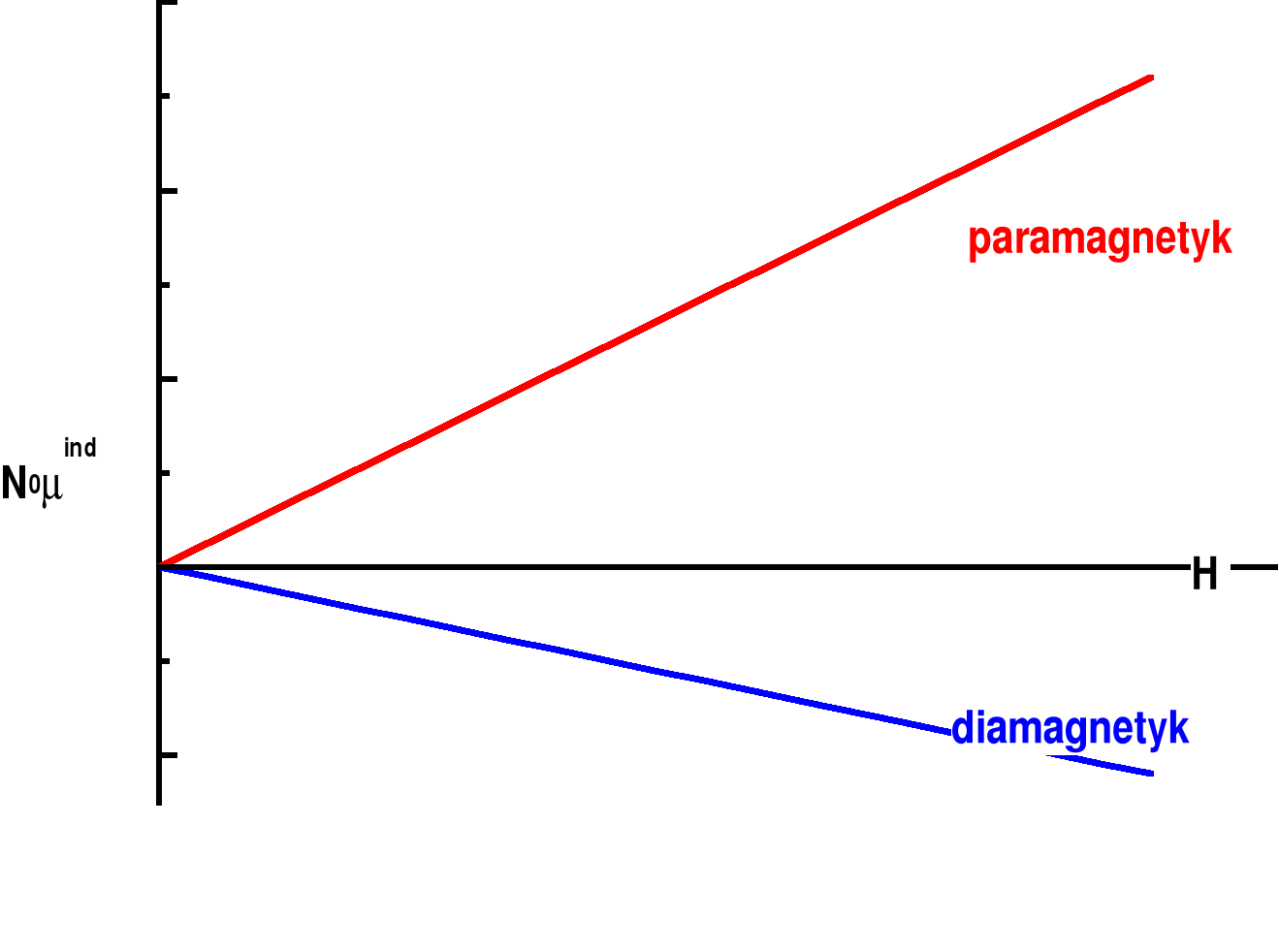
Namagnesowanie można zmierzyć za pomocą wagi magnetycznej Gouya.
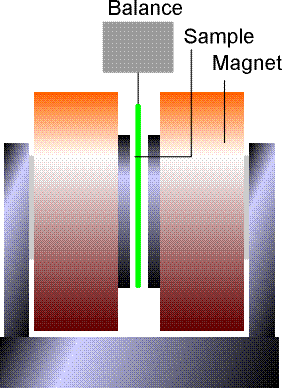
Cylindryczna próbka o przekroju S, jest umieszczona w polu magnetycznym o natężeniu H.
Po włączeniu pola magnetycznego substancja paramagnetyczna pozornie jest cięższa, natomiast substancja diamagnetyczna pozornie staje się lżejsza.
Siła działająca na próbkę zależy od natężenia pola magnetycznego oraz różnicy podatności magnetycznych próbki χm i ośrodka χo:
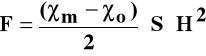
Diamagnetyki
Cząsteczki nie maja trwałego momentu magnetycznego, natomiast ulegają namagnetyzowaniu w polu magnetycznym.
Trwałego momentu magnetycznego nie wykazują atomy i jony o zamkniętych powłokach elektronowych: s2, p6, d10, f14
Podatność magnetyczną χ można określić w oparciu o teorię P.Langevina (1905):
![]()
nat - liczba atomów, χat - podatność magnetyczna atomu
λi - poprawka konstytucyjne (określa wpływ otoczenia na podatność magnetyczną atomu).
Podatność magnetyczna atomu χat zależy od liczby elektronów nel oraz odległości elektronu od jądra roi:
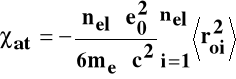
Diamagnetyki wykazują zjawisko anizotropii - różne właściwości magnetyczne w różnych kierunkach:
|
-χ1. 106 |
-χ1. 106 |
-χ1. 106 |
Benzen |
37,3 |
37,3 |
91,3 |
Naftalen |
56,1 |
53,9 |
169,0 |
Antracen |
75,8 |
62,6 |
251,8 |
Paramagnetyki
Cząsteczki paramagnetyków mają trwały moment magnetyczny m. Namagnesowanie paramagnetyków w polu magnetycznym można określić na podstawie teorii Langevina
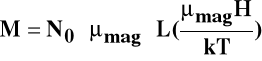
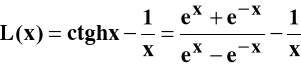
Jeżeli natężenie pola magnetycznego H jest stałe i duże, spełniony jest warunek 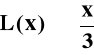
, namagnesowanie paramagnetyków określa zależność:
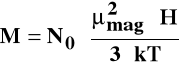
Podatność magnetyczną określa prawo Curie (1895):
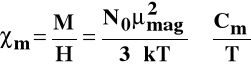
Cm jest stałą Curie.
Moment magnetyczny atomu jest konsekwencją:
moment magnetycznego związanego ze spinem elektronów,
orbitalnych momentów magnetycznych elektronów,
momentów magnetycznych jąder.
Moment magnetyczny wynikający ze spinów elektronów:
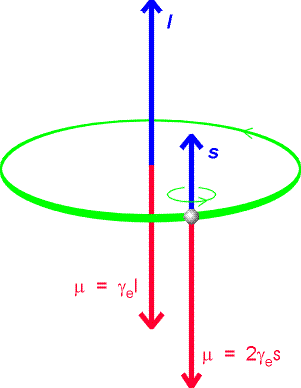
Ruch ładunków elektrycznych wywołuje pole magnetyczne.
Moment magnetyczny związany ze spinem elektronu:
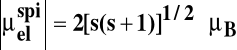
Magneton Bohra:
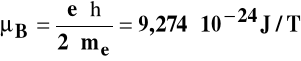
Orbitalny moment magnetyczny elektronu
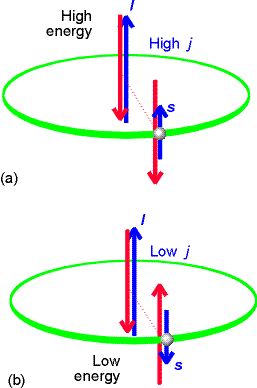
Moment magnetyczny jest anty- równoległy i proporcjonalny do orbitalnego momentu pędu:
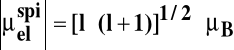
Sprzężenie spinowo orbitalne jest skutkiem oddziaływania momentów magnetycznych spinowego i orbitalnego.
Jeżeli momenty pędu, spinowy i orbitalny, są równoległe oddziaływanie jest niekorzystne -wypadkowa wewnętrzna liczba spinowa j, - określająca całkowity moment pędu, jest duża, jeżeli momenty pędu są antyrównoległe całkowity moment pędu jest mały:
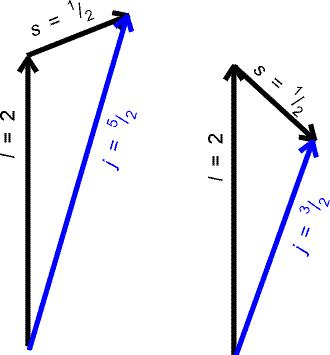
Sprzężenie spinowego i orbitalnego momentu pędu daje dwie różne wartości wypadkowej liczby kwantowej j, zależnie od wzajemnej orientacji pędów.
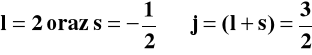
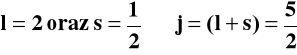
Moment magnetyczny cząsteczki zależy od wypadkowej wewnętrznej liczby kwantowej J, która określa całkowity moment pędu i jest sumą orbitalnych momentów pędu L i momentów magnetycznych niesparowanych elektronów S:
![]()
g(J,L,S) - współczynnik spektroskopowy Landego, sprzężenie momentów magnetycznych:
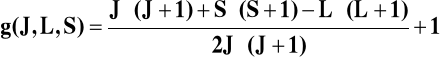
Moment magnetyczny jądra μI
Cechą charakterystyczną jądra jest jego liczba kwantowa I, która może przyjmować dodatnie wartości połówkowe lub całkowite.
Moment pędu jądra:
![]()
Magneton jądrowy: 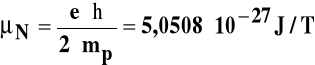
.
Jeżeli liczba kwantowa jądra spełnia warunek I>0 jądro ma stały moment magnetyczny i w polu magnetycznym zachowuje się jak magnes. Energia oddziaływania pola magnetycznego o natężeniu H na jądro o momencie magnetycznym μI:
![]()
μZ -składowa momentu magnetycznego jądra zgodna z kierunkiem pola, IZ - dozwolona składowa spinu jądra zgodna z kierunkiem pola.
Moment pędu jądra jest skwantowany i wartości IŻ nie mogą być dowolne, co wykazało doświadczenie Sterna i Gerlacha.
Z teorii klasycznej można oczekiwać, że pole magnetyczne powoduje dowolne odchylenie jądra obdarzonego trwałym momentem magnetycznym zgodnie z orientacją magnesu w polu, która określa kąt θ:
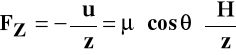
Doświadczenie Sterna i Gerlacha wykazało, że:
![]()
Liczba stanów dozwolonych dla składowej spinu jądra wynosi (2I+1), gdyż określa ją spinowa liczba kwantowa.
Jeżeli I = 1/2 dozwolone są stany: +1/2 oraz -1/2
Jeżeli I = 1 dozwolone są stany: +1, 0 , -1
Spinowa liczba kwantowa jest wypadkową spinów neutronów, protonów i elektronów.
Spinowa liczba jądrowa przyjmuje wartości zerowe dal jąder o parzystej liczbie protonów i neutronów I=0 np. 12C, 16O
Niezerowe spinowe liczby jądrowe mają jądra o nieparzystej liczbie protonów I≠0 lub nieparzystej liczbie neutronów I≠0.
Energię oddziaływania pola magnetycznego o natężeniu H na jądro o niezerowej spinowej liczbie jądrowej współczynnik proporcjonalności nazywany czynnikiem jądrowym gI, który jest wyznaczany doświadczalnie i może przyjmować wartości dodatnie, co oznacza, że moment magnetyczny i spin jądra mają ten sam kierunek, lub ujemne, gdy kierunki momentu magnetycznego i spinu są przeciwne.
Energię oddziaływania pola magnetycznego można wyrazić zastępując czynnik jądrowy gI stosunkiem magnetogirycznym jądra γI:
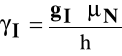
Jadro |
Spin I |
gI |
γI.107 T-1s-1 |
1H (99,98) |
1/2 |
5,585 |
26,753 |
2H (0.02) |
1 |
0,857 |
4,107 |
7Li |
3/2 |
2,171 |
10,398 |
13C (1,11) |
1/2 |
1,405 |
6,728 |
14N (96,64) |
1 |
0,403 |
1,934 |
15N |
1/2 |
-0,567 |
-2,712 |
17O |
5/2 |
-0,757 |
-3,628 |
19F |
1/2 |
5,257 |
25,179 |
neutron |
1/2 |
-3,826 |
-18,32 |
Podstawy magnetycznego rezonansu jądrowego
Rozpatrzmy energię protonu w polu magnetycznym.
Jeżeli moment magnetyczny protonu jest antyrównoległy, I = -1/2, do pola magnetycznego o natężeniu H:
![]()
Jeżeli moment magnetyczny protonu jest równoległy, I = 1/2, do pola magnetycznego o natężeniu H:
![]()
Różnica energii stanów α oraz β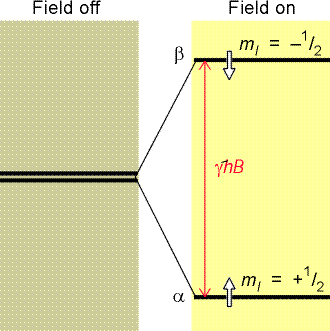
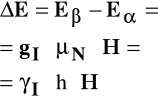
zależy od natężenia pola H.
Energię protonu w polu magnetycznym można określić za pomocą częstości Larmora νL:
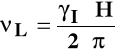
Częstość Larmora jest tym większa, im większe natężenie pola.
Dla protonu w polu 12 T częstość Larmora wynosi około 500 MHz
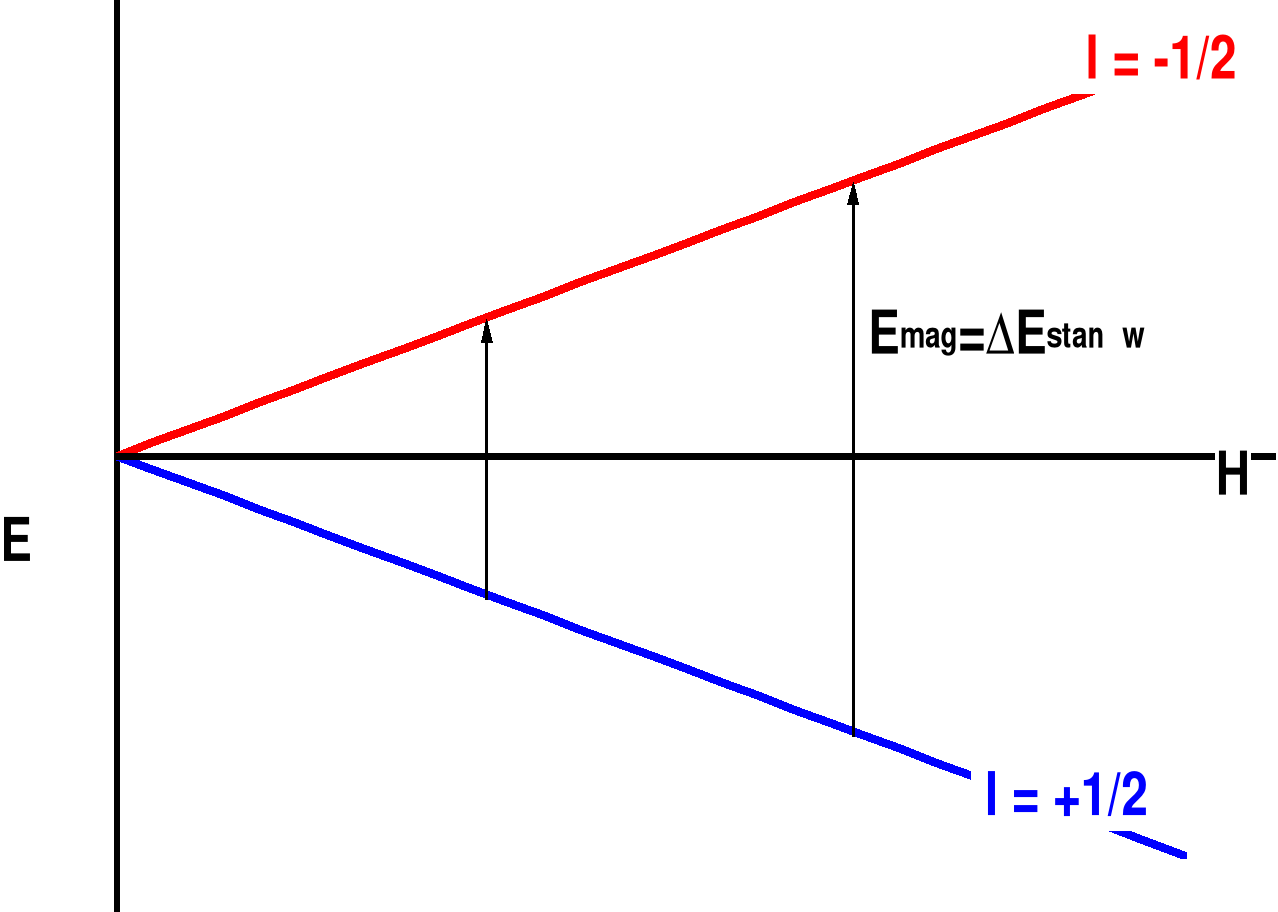
Dla większości jąder stosunek magnetogiryczny jest dodatni i energia stanu α jest wyższa od energii stanu β, a populacja stanów β jest nieznacznie większa od populacji stanów α. Stosunek populacji stanów określa rozkład Boltzmanna:
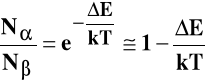
Stąd można obliczyć zależność różnicy obsadzeń stanów od energii oddziaływania natężenia pola:
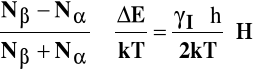
Jeżeli do próbki dostarczymy energię promieniowania ![]()
, która odpowiada różnicy energii stanów (Eα - Eβ), skutkiem absorpcji jest zmiana populacji stanów.
Częstość rezonansowa νrez zależy od natężenia pola H:
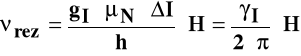
Rezonans magnetyczny
Próbka umieszczona w stałym polu magnetycznym o natężeniu H → dobieramy częstość rezonansową fali elektromagnetycznej νrez.
Próbka oświetlona falą elektromagnetyczną o stałej częstości ν → dobieramy natężenie pola magnetycznego H.
Energia jest absorbowana jeżeli częstość fali elektromagnetycznej (radiowej) odpowiada częstości rezonansowej. Zaabsorbowana energia jest proporcjonalna do H oraz do różnicy populacji stanów (Nβ - Nα), która jest proporcjonalna do H → rejestrowany sygnał jest proporcjonalny do H2
Częstości rezonansowe jąder w polu o natężeniu 14094 G:
Jądro |
νrez (MHz) |
Względna czułość (dla tej samej liczby spinów) |
1H |
60,00 |
1,00 |
2H |
9,2104 |
9,65.10-3 |
7Li |
23,317 |
0,293 |
13C |
15,317 |
1,59.10-2 |
14N |
4,3343 |
1,01.10-3 |
15N |
6,3343 |
1,04.10-3 |
17O |
8,314 |
2,91.10-2 |
19F |
56,446 |
0,833 |
Przesunięcie chemiczne
Lokalne pole magnetyczne działające na jądrowy moment magnetyczny może różnić się od zewnętrznego pola magnetycznego. Zewnętrzne pole magnetyczne indukuje orbitalny moment pędu elektronów, który powoduje powstanie małego dodatkowego pola δH. To dodatkowe pole jest proporcjonalne do pola zewnętrznego:
![]()
σ jest stałą przesłaniania (ekranowania), która zależy od struktury elektronowej w pobliżu danego jądra. Obliczenie wiarygodnej stałej ekranowania jest trudne, natomiast kierunki zmian stałej wskutek zmian otoczenia jądra są dobrze poznane.
Lokalne pole działające na jądro jest inne niż pole zewnętrze:
![]()
Skutkiem zmiany pola działającego na jądro jest zmiana częstości Larmora:
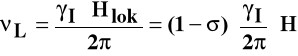
Częstość Larmora zależy od otoczenia jądra i dlatego można rozróżniać jądra tego samego pierwiastka znajdujące się w różnych otoczeniach.
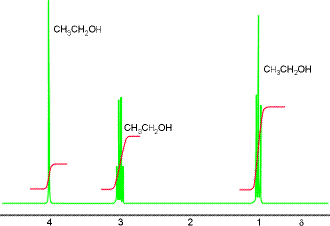
Wpływ otoczenia na częstość rezonansową charakteryzuje stosunek różnicy częstości rezonansowej jądra w danym otoczeniu ν i wzorca ν0, względem częstości rezonansowej wzorca, nazwana przesunięciem chemicznym δ:
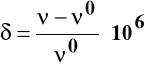
Wzorcem dla protonów jest częstość rezonansowa dla protonów w tetrametylosialnie Si(CH3)4, wzorcem 13C jest częstość rezonansowa 13C w tetrametylosialnie Si(CH3)4, wzorcem 31P jest częstość rezonansowa 31P w 85% wodnym roztworze H3PO4.
Przesunięcie chemiczne δ zależy od stałej ekranowania σ:
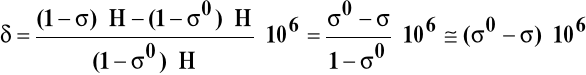
Jeżeli ekranowanie maleje, przesunięcie chemiczne rośnie. Jądra o dużym przesunięciu chemicznym są silnie odsłaniane.
Stała przesłaniania, obserwowana doświadczalnie, zależy od:
σ(lokalna) - wpływu elektronów związanych z rozważanym jądrem,
σ(otoczenie) - wpływu sąsiadujących z jądrem grup atomów,
σ(rozpuszczalnik) - wpływu cząsteczek rozpuszczalnika.
Wpływ elektronów na stałą przesłaniania jest sumą dodatniego udziału diamagnetycznego σd i ujemnego udziału paramagnetycznego σp: σ(lokalna) = σd + σp.
σd zależy od gęstości elektronowej w pobliżu jądra → zewnętrzne pole wywołuje ruch elektronów, co powoduje wytworzenie pola magnetycznego:
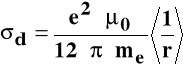
σp jest odwrotnie proporcjonalna do różnicy energii Δ orbitali HOMO (highest filled molecular orbital) i orbitali LUMO (lowest unfilled molecular orbital) gdyż w polu magnetycznym elektrony ulegają wzbudzeniu (duży efekt paramagnetyczny wykazują małe atomy o niskich energiach wzbudzenia):
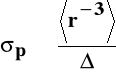
Wpływ grup otaczających na stałą przesłaniania zależy od podatności magnetycznej grupy
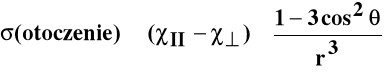
Pole magnetyczne, indukując prądy w rozkładach elektronów, wywołuje moment magnetyczny proporcjonalny do pola, którego wielkość zależy od podatności magnetycznej χ.
Indukowany moment wytwarza pole, w położeniu jądra, którego natężenie zależy od:
odległości jądra od grupy atomów r-3
różnicy podatności magnetycznej w kierunku równoległym i prostopadłym do grupy (χII -χ⊥)
kąta θ, utworzonego pomiędzy wektorem łączącym grupę z jądrem magnetycznym a osią symetrii grupy.
Wpływ grup sąsiadujących może być dodatni lub ujemny, zależnie od różnicy (χII -χ⊥) oraz cosθ.
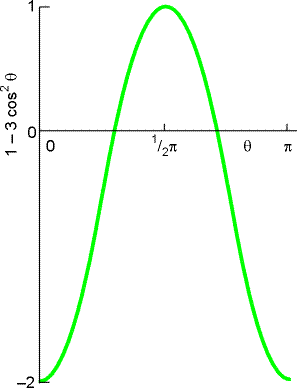
Jeżeli 54,7o < θ < 125,3o
![]()
Subtelna struktura sygnału NMR
Wysokorozdzielczy NMR pozwala zaobserwować rozszczepienie linii wskutek oddziaływań spinów. Wielkość oddziaływań wyraża stała sprzężenia skalarnego J, która jest niezależna od natężenia przyłożonego pola.
Rozważmy cząsteczkę AX, zawierającą dwa jądra znacznie różniące się przesunięciami chemicznymi.
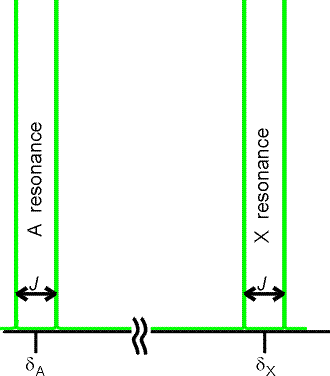
Częstość rezonansowa jądra A, w pobliżu którego jest jądro X o spinie -1/2, częstość rezonansowa jądra A przesunie się o +1/2J, natomiast jeżeli spin jądra X jest +1/2, częstość Larmora przesunie się o -1/2J. Skutkiem przesunięć jest rozszczepienie sygnału na dwie linie odległe o J.
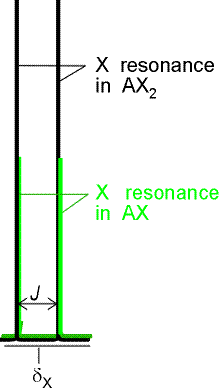
Rozważmy cząsteczkę AX2 - obecność dwóch jąder X nie wpływa na rozszczepienie sygnału, gdyż rozszczepienie sygnału jest skutkiem wpływu jądra A na częstość rezonansową jądra X, wpływa natomiast na intensywność sygnału.
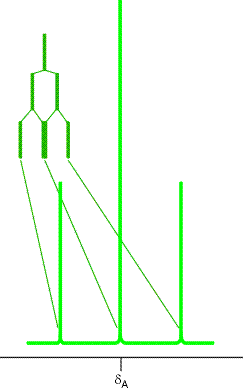
Obecność dwóch jąder X wpływa na rozszczepienie sygnału jądra A, gdyż pod wpływem jądra X sygnał jądra A ulega rozszczepieniu, a drugie jądro X rozszczepia każdą z linii dubletu.
Skutkiem takiego rozszczepienia jest tryplet, w którym intensywności sygnałów określa stosunek 1:2:1
Techniki impulsowe w NMR
Spektroskopia NMR z transformacja Fouriera - obserwujemy promieniowanie emitowane przy powrocie spinów jądrowych do stanu równowagi, który został zaburzony.
Wypadkowy moment pędu próbki, zawierającej wiele jąder o spinie ½, można przedstawić jako wektor o długości [I(I+1)]1/2, leżący na pobocznicy stożka wokół osi z. Dla I=1/2 długość wektora wynosi ½(3)1/2 i tworzy z osią kat 55o:
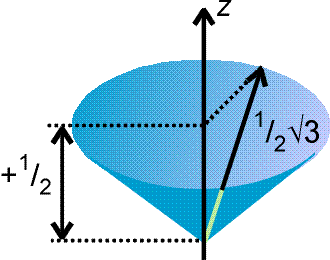
W zewnętrznym polu poszczególne wektory wykonują precesję z częstością Larmora.
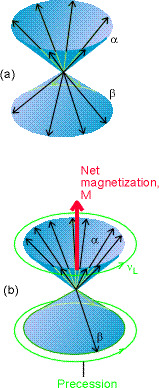
Bez pola magnetycznego liczby spinów α i β są takie same a ich rozłożenie wokół osi z jest przypadkowe - wypadkowe namagnesowanie jest zero
W stałym zewnętrznym polu magnetycznym zmienia się namagnesowanie próbki wskutek zmiany obsadzenia stanów -wzrasta liczba stanów α (o mniejszej energii):
Wektor namagnesowania M jest skierowany wzdłuż osi z, a jego długość jest proporcjonalna do różnicy populacji stanów α i β.
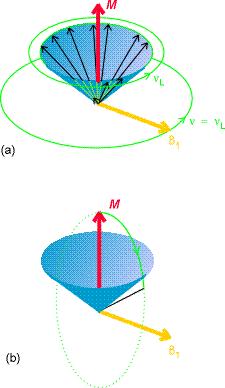
Na próbkę działa zmienne pole magnetyczne, o częstości radiowej, spolaryzowane kołowo w płaszczyźnie xy (prostopadłej do wektora namagnesowania). Jeżeli częstość oscylacji pola jest równa częstości rezonansowej, wektor namagnesowania znajduje się w stałym polu o natężeniu B1, ponieważ wirujące pole nadąża z precesją spinów. Po wpływem tego stałego pola wektor namagnesowania wykonuje precesję wokół B1z szybkością proporcjonalną do B1
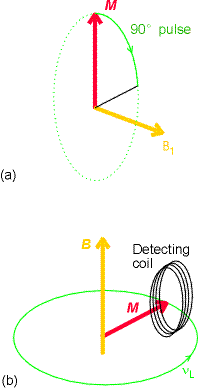
Jeżeli pole B1 jest przyłożone jako impuls o odpowiednio dobranym czasie trwania wektor namagnesowania M znajdzie się w płaszczyźnie xy (impuls π/2).
Wektor M wirując w płaszczyźnie xy indukuje sygnał w cewce odbiornika.
Ponieważ pole B1 przyłożono impulsowo, po wyłączeniu pola, wektor namagnesowania maleje, ze stałą czasową T2. Obserwujemy malejący oscylujący sygnał precesji swobodnej.
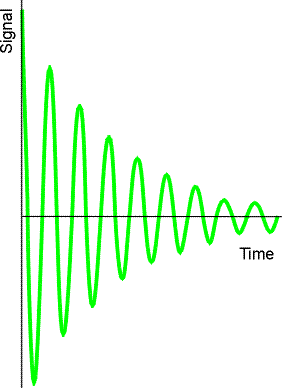
Składowa namagnesowania w kierunku y zmienia się w sposób opisany równaniem:
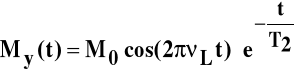
Proces zaniku namagnesowania w płaszczyźnie xy jest procesem relaksacji spinowej. T2 jest czasem relaksacji spin-spin.
Elektronowy rezonans paramagnetyczny EPR (ESR)
Spektroskopia EPR ogranicza się do cząsteczek, które zawierają niesparowany elektron i są paramagnetyczne.
Paramagnetyczne są cząsteczki:
zawierające paramagnetyczne atomy: atomy pierwiastków ziem rzadkich lub atomy pierwiastków przejściowych, np. jony Fe3+ lub [Fe(CN)6]3-,
rodniki czyli cząsteczki zawierające niesparowane elektrony zewnętrzne; rodniki mogą powstawać w reakcji chemicznej lub wskutek wzbudzenia elektronowego jako twory nietrwałe, znane są także trwałe rodniki np. DPPH (difenylo-pikrylohydrazyl),
cząsteczki w stanie trypletowym, który jest stanem trwałym np. O2, NO, NO2 lub nietrwałym stanem wzbudzonym np. w naftalenie.
Moment magnetyczny elektronu ![]()
, gdzie
gS=2.0023 dla swobodnego elektronu, w zewnętrznym polu magnetycznym ma dwie możliwe orientacje, wyznaczone przez magnetyczną liczbę kwantową, mS = ± ½, które różnią się energią, zależną od pola magnetycznego B:
![]()
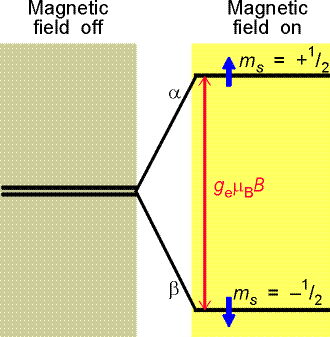
Energia elektronu w stanie α, któremu odpowiada mS= + ½ wzrasta ze wzrostem pola, natomiast energia elektronu w stanie β, któremu odpowiada mS= - ½ maleje ze wzrostem pola. Różnice energii wynosi ![]()
.
Próbka, umieszczona w polu magnetycznym, absorbuje falę elektromagnetyczną, jeżeli spełniony jest warunek rezonansu:
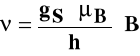
Typowe pole magnetyczne, stosowane w pomiarach EPR, wynosi około 0,3 T, spełnia warunek rezonansu dla częstości 10 GHz, co odpowiada fali o długości 3 cm.
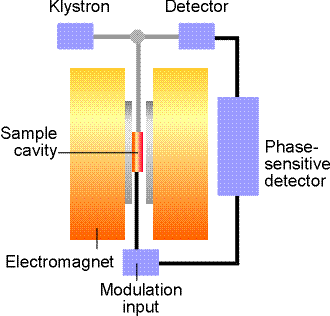
Próbkę w kwarcowym lub szklanym pojemniku umieszcza się we wnęce rezonansowej. Pomiar polega na monitorowaniu absorpcji mikrofal, których źródłem jest klistron, dla zmieniającego się pola magnetycznego.
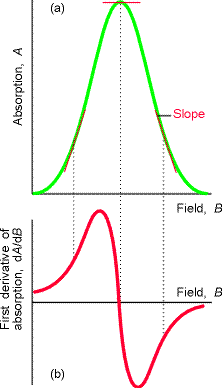
Sygnał rejestrowany jest nie jako krzywa absorpcji, lecz jej pierwsza pochodna.
Największej absorpcji odpowiada zerowa wartość pierwszej pochodnej, czyli punktowi, w którym krzywa przechodzi przez zero.
Spinowy moment magnetyczny oddziałuje z polem lokalnym, więc warunek rezonansu należy zapisać jako:
![]()
g jest czynnikiem rodnika lub kompleksu i różni się od wartości gS dla swobodnego elektronu, zależy bowiem od struktury elektronowej rodnika lub kompleksu.
Struktura nadsubtelna widm EPR
Nadsubtelna struktura widm EPR jest skutkiem rozszczepienia linii rezonansowych na składowe. Przyczyną rozszczepienia jest oddziaływanie magnetyczne spinu elektronu z magnetycznymi momentami jąder.
Lokalne pole magnetyczne działające na elektron:
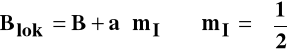
gdzie a jest stałą sprzężenia nadsubtelnego.
Połowa rodników ma spin mI = + ½, dlatego jest w rezonansie, gdy pole spełnia warunek:
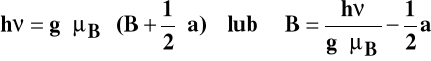
Druga połowa ma spin mI = - ½, dlatego jest w rezonansie, gdy pole spełnia warunek:
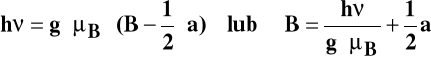
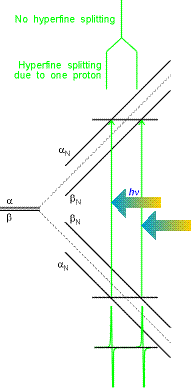
Odziaływanie elektronu z jądrem o spinie ½ prowadzi do pojawienia się czterech poziomów energetycznych (zamiast początkowych dwóch). Dlatego widmo składa się z dwóch linii o jednakowej intensywności.
gdy w rodniku występuje kilka jaer magnetycznych, każde z nich wnosi wkład w strukturę nadsubtelną. W przypadku równowaznych protonów niektóre z linii nakładają się. Jeżeli rodnik zawiera N protonów równoważnych pojawi się N+1 linii o rozkładzie intensywności określonym trojkątem Pascala.
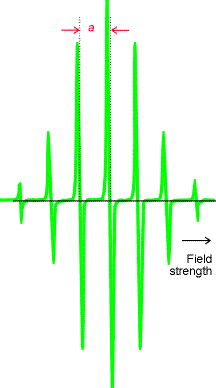
Widmo EPR anionorodnika benzenu C6H6- w roztworze.
Intensywności linii określa stosunek:
1: 6 : 15 : 20 : 15 : 6 : 1, wynikający z odziaływania sześciu równowaznych protonów.
Wyszukiwarka
Podobne podstrony:
mmgg, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II sprawka
spr57, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy
Moje 50 , Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II spr
monia 11, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II spr
15 wyznaczanie ciepła spalania, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, Chem
KOND41vmac, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II s
rad, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II sprawka
spr15, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy
Do druku askorbinowy, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczn
Elektroda szklana, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna c
Podczas wymuszonego przep+éywu p+éynu, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wsz
27 poprawa 2, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, Chemia fizyczna
POLSKI, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II spraw
spr26, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy
lab50as, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II spra
hk spr numer 23, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz
11 wyznaczanie ciepła rozpuszczania, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy,
więcej podobnych podstron