AUTOMATYKA NAPĘDU ELEKTRYCZNEGO

1. Wskaźniki jakości sterowania układów napędowych

Są wskaźnikami odnoszącymi się do syntezy układów sterowania silników elektrycznych, której zadaniem jest teoretyczne projektowanie układów sterowania napędów elektrycznych. Do przeprowadzenia syntezy niezbędna jest znajomość:

- modelu matematycznego SE wraz z MR oraz przekształtnikiem zasilającym;

- określenia zadania i wymagań, jakie ma spełniać UN

- charakterystyk zakłóceń działających na układ np. zmiany momentu obciążenia, spadki napięcia w zasilaniu;

- wskaźników jakości sterowania;

- ograniczeń dotyczących sygnałów wymuszających, elektromagnetycznych oraz mechanicznych zmiennych stanu.

Ze względu na nadmierne komplikacje dokładnych metod syntezy, bądź brak możliwości realizacji praktycznej regulatorów optymalnych, stosuje się szereg uproszczeń modeli matematycznych silników, przekształtników, sformułowań wskaźników jakości sterowania oraz rodzajów i struktur regulatorów.

Ogólna postać wskaźnika jakości sterowania: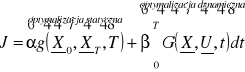
; gdzie: ၡ,ၢ - współczynniki wagi; ၡ,ၢ჎<0,1>, g,G - funkcje kosztów sterowania, X₀,X_T - wektory stanu dla t=0 i t=T, U - wektor sterowania

; Minimalizacja J₁ - zapewnia w stanach ustalonych stałą wartość strumienia ၙ_S; Minimalizacja J₂ - odpowiada w przypadku np. maszyn prądu przemiennego - warunkowi cosၪ ≈1 (minimalizacja w sensie energetycznym przekształtnika zasilającego); Minimalizacja J₃ - daje rozszerzenie J₁ (dynamiczne) - stabilizacja zadanego ၹ_S również w stanach dynamicznych; Minimalizacja J₄ - zapewnia dobrą dynamikę i tłumienie momentu m; Minimalizacja J₅ - zapewnia szybką i dobrze tłumioną regulację prędkości kątowej zarówno przy zmianach wymuszeń jak i zakłóceń.

2. Różnica pomiędzy optymalizacją statyczną i dynamiczną; struktury regulacji momentu elektromagnetycznego

- Optymalizacja statyczna: Polega ona na zaprojektowaniu odpowiednich bloków lub struktur regulacji, które umożliwiają uzyskanie w stanie ustalonym stabilizacji lub wartości ekstremalnych wybranych wskaźników statycznych.

- Optymalizacja dynamiczna układów napędowych: Podstawowy cel - uzyskanie dobrej dynamiki (szybkich i dobrze tłumionych przebiegów) przy przejściu od stanu początkowego do końcowego. Spośród dostępnych sygnałów sterujących wybieramy te zapewniające najlepsze właściwości dynamiczne układu. Dla wybranego rodzaju sygnału określamy taki jego przebieg by czas przejścia od stanu początkowego x₀(t) do końcowego x_k(t) był jak najkrótszy (poprzez dobór regulatorów i ich nastaw).

Moment elektromagnetyczny może być sterowany przy zastosowaniu czterech podstawowych struktur regulacji:

1. struktura z wymuszeniem napięcia (układ bezpośredniego sterowania prędkością);

Układ ten charakteryzuje się słabą dynamiką regulacji momentu, bo brak jest sprzężeń od zmiennych stanu tworzących moment silnika - przebiegi dynamiczne momentu nie są kontrolowane.

2. struktura równoległa;

Układ zapewnia kontrole sygnałów równoległych, lecz sterowana jest jedynie jedna wielkość (zmienna stanu) z aktualnego regulatora (wybierana przez sumator logiczny);

3. struktura szeregowa;

4. z podporządkowaną regulacją momentu.

3. Kryteria optymalnych nastaw regulatorów liniowych

Zadaniem regulacji automatycznej jest spełnienie dwóch podstawowych zadań: by przebieg wielkości regulowanej dokładnie odwzorowywał przebieg wielkości zadanej oraz by do minimum ograniczyć wpływ zakłóceń na wielkość regulowaną.

- Kryterium całkowe wyraża się więc funkcją: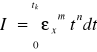
; gdzie: t_k - czas zakończenia procesu regulacji; przyjmuje się t_k = ∞, m=1,2; n=0,1,2.

- Kryterium ISE - całka minimalnej wartości średniej błędu kwadratowego: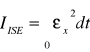
. Przy zastosowaniu tego kryterium do układu regulacji zamkniętej o transmitancji G(p)=l/(l+2ၸp+p²), uzyskuje się: współczynnik tłumienia ၸ=0,5; przeregulowanie ၳ_x=16%.

- Kryterium ITSE - całka z iloczynu kwadratu uchybu wielkości regulowanej i czasu: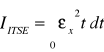
. Kryterium to powoduje, że uzyskuje się większe tłumienie oscylacji wielkości regulowanej w dalszych przedziałach czasowych.

- Kryterium IAE - całka wartości modułu uchybu wielkości regulowanej: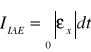
.Przy zastosowaniu tego kryterium dla układu o zamkniętej o transmitancji operatorowej G(p)= 1/(1+2ၸp+p²) otrzymuje się współczynnik tłumienia ၸ=1.

- Kryterium ITAE - całka z iloczynu czasu i wartości modułu uchybu wielkości regulowanej: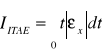
. ottrzymujemy: współczynnik tłumienia, przeregulowanie ၳx =4%, czas narostu tn = 4,7 Ts, czas regulacji tr = 8,4 Ts (przy dokładności ± 2%).

- Kryterium modułu odnosi się do przebiegu charakterystyki częstotliwościowej układu zamkniętego. Charakterystyka amplitudowo-częstotliwościowa powinna w swym przebiegu, w szerokim paśmie w mieć wartość stałą - bliską jedności:

Transmitancja regulatora PI:
; gdzie: KR - współczynnik wzmocnienia (proporcjonalności), TR - czas zdwojenia, TC = TR / KR - stała całkowania regulatora . Zgodnie z kryterium modułu, nastawy regulatora dobiera się wg następujących zależności:

. Stała całkowania regulatora:
. Dla układu otwartego:
. Transmitancja układu zamkniętego zoptymalizowanego wg kryterium modułu:
. Wielkości charakterystyczne odpowiedzi wielkości regulowanej na skok jednostkowy wielkości zadanej są następujące: czas narastania tn = 4.7 Ts; przeregulowanie s x = 4% ; czas uspokojenia tu = 8.4 Ts (przy dokładności 2%). Układ nastrojony wg kryterium modułu charakteryzuje się: małym przeregulowaniem, znacznym tłumieniem, krótkim czasem narostu,

KM nie nadaje się do strojenia obwodu, który poza członem inercyjnym zawiera człon całkując. Występują wówczas nietłumione oscylacje - układ niestabilny.

- Kryterium symetrii

Obiekt zawiera kilka członów inercyjnych I rzędu o małych stałych czasowych Ti oraz jeden człon całkujący:

; gdzie: TO - stała całkowania, Ts - zastępcza stała czasowa obiektów inercyjnych. Nastawy regulatora PI zgodnie z kryterium symetrii, dobiera się wg następujących zależności:
;
. Stała całkowania regulatora wynosi: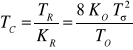
. Transmitancja układu otwartego:
. Transmitancja układu zamkniętego zoptymalizowanego wg kryterium symetrii:
; czas narastania tn = 3.1 Ts; przeregulowanie s x = 43% ; czas uspokojenia tu = 16.5 Ts (przy dokładności ± 2%).

4. Model matematyczny, transmitancje silnika obcowzbudnego prądu stałego

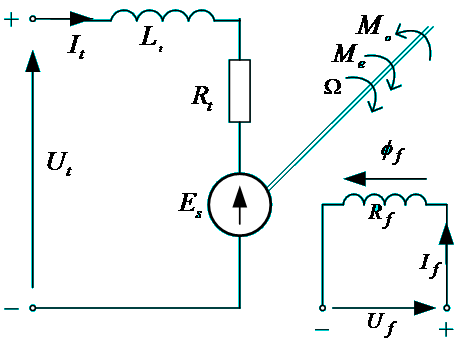
Równanie napięciowe obwodu wzbudzenia:
; równanie napięciowe obwodu twornika
; równanie ruchu:
; zależność na charakterystykę magnesowania:
;  zależność na siłę elektromotoryczną twornika: E_s
; równanie na moment elektromagnet. silnika: M_e
. Model matematyczny w jednostkach względnych:
;
;
;
; gdzie:
- współczynnik wzmocnienia obwodu twornika silnika prądu stałego;
- stała elektromagnetyczna obwodu twornika;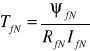
- stała elektromagnetyczna obwodu wzbudzenia;
- stała mechaniczna;
- nieliniowa charakterystyka magnesowania. - -

- Transmitancja przewodnia prędkościowa:
;

- Transmitancja przewodnia prądowa:
; gdzie: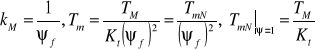

- Transmitancja zakłóceniowa prędkościowa:
; -

- Transmitancja zakłóceniowa prądowa
; gdzie: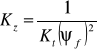
;

- Pulsacja drgań własnych wynosi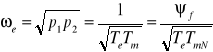
;

- Współczynnik tłumienia jest równy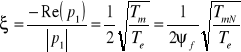

Schemat strukturalny silnika obcowzbudnego prądu stałego w jednostkach względnych

5. Wpływ strumienia wzbudzenia na właściwości dynamiczne (r. charakterystyczne transmitancji) silnika prądu stałego

Pierwiastki równania charakterystycznego:
wynoszą: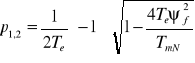
; gdzie: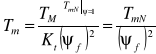
-

Transmitancja przewodzenia w stanie ustalonym: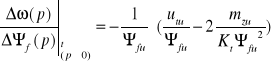
. Dopóki
czyli
to prędkość w rośnie, gdystrumień Ψ_f maleje. Natomiast gdy:
i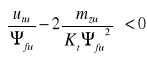
to prędkość będzie maleć pomimo, że strumień też maleje. Dalsze obniżanie strumienia nie spowoduje oczekiwanego wzrostu prędkości. A więc przy obniżaniu strumienia wzbudzenia:

- następuje wzrost elektromechanicznej stałej czasowej silnika: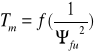

- SPS wykazuje większą wrażliwość na zmiany momentu obciążenia: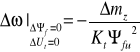

6. Możliwości realizacji wskaźników optymalizacji statycznej w napędzie prądu stałego

Wskaźniki optymalizacji statycznej dla SPS:

Minimalizując wskaźnik J1 :
; czyli przy sterowaniu przy zachowaniu stałej, znamionowej wartości strumienia (prądu) wzbudzenia - sterowanie prędkością przez zmianę napięcia twornika przy Yf = const.

Minimalizując wskaźnik J2 :
; czyli:
a więc, gdy strumień wzbudzenia jest prostopadły do kierunku prądu twornika:

Silnik musi posiadać uzwojenia kompensujące reakcję twornika - nie trzeba wówczas specjalnego sterowania!

Na podstawie ogólnego podziału struktur regulacji momentem można wyróżnić następujące struktury sterowania prędkością i momentem SPS:

1 - struktura szeregowa (kaskadowa),

2 - struktura równoległa (sprowadza się do struktury bezpośredniego wymuszenia napięcia twornika),

3 - struktura z podporządkowaną regulacją momentu (odmiana struktury szeregowej).

7. Napędy przekształtnikowe prądu stałego: struktura szeregowa, równoległa - różnice we właściwościach dynamicznych

- struktura szeregowa

Schemat blokowy obwodu regulacji prędkości

- stała czasowa twornika Te została skompensowana przez regulator prądu Ri (KM)

- obwód regulacji prądu staje się w przybliżeniu członem inercyjnym pierwszego rzędu o zastępczej stałej czasowej Tzi

- w zoptymalizowanym obwodzie regulacji prądu, pozostały nieskompensowane tylko małe stałe czasowe.

Układ zoptymalizowany charakteryzuje się krótkim czasem narostu tn = 3,1TZi, z pierwszym przeregulowaniem prędkości ၤ > 43% oraz czasem regulacji (przy założonej dokładności rzędu 2%) tr=16,5TZi. W celu zmniejszenia przeregulowania sygnał zadający podaje się poprzez filtr w zadajniku prędkości:
. Odpowiedź prędkości na skokową zmianę sygnału zadanego w tak zoptymalizowanym układzie regulacji charakteryzuje się przeregulowaniem rzędu ၤ ၀ 8%, czasem narastania tn=7,6TZi oraz czasem ustalania tr=13,3TZi.

W wyniku działania regulatorów PI prądu i prędkości uzyskuje się kompensację dwóch podstawowych dużych stałych czasowych napędu: stałej elektromagnetycznej obwodu twornika Te (Ri), stałej mechanicznej TM (Rw), nieskompensowana stała czasowa Tzi składa się ze stałej czasowej związanej z opóźnieniem przekształtnika oraz stałej Ti wynikającej z opóźnienia układu pomiaru prądu.

W strukturze szeregowej kontrolowane i sterowane są dwie zmienne stanu silnika: prędkość kątowa i prąd twornika.

- struktura równoległa

W wyniku działania regulatora PI prędkości uzyskuje się: kompensację tylko stałej czasowej mechanicznej TM. Nieskompensowana jest stała czasowa elektromagnetyczna Te i ona decyduje o właściwościach dynamicznych napędu w normalnych.

W strukturze równoległej sterowana jest tylko jedna zmienna stanu silnika - prędkość kątowa, a prąd twornika jest tylko kontrolowany

Porównanie obu struktur:

Transmitancje opisujące obie struktury mają podobną postać. W obu strukturach stała czasowa mechaniczna TM nie ma wpływu na właściwości dynamiczne zamkniętego obwodu regulacji prędkości (została skompensowana przez Rw ). W strukturze szeregowej (z podrzędnym regulatorem prądu) - o dynamice decyduje zastępcza stała czasowa obwodu regulacji prądu Tzi (zależna od stałej przekształtnika). W strukturze równoległej - o dynamice decyduje elektromagnetyczna stała czasowa Te twornika SPS.

8. Możliwości realizacji wskaźników optymalizacji statycznej w napędzie z SI

Wskaźnik optymalizacji statycznej dla napędu z SI:

Minimalizacja składnika I1:

Minimalizacja składnika I1 prowadzi więc do sterowania maszyny z zachowaniem stałej, znamionowej amplitudy strumienia skojarzonego z uzwojeniem stojana (lub wirnika).

Składnik I2 ma postać:

Warunkiem minimalizacji: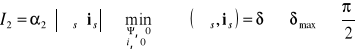

W maszynie indukcyjnej kąt obciążenia ၤ nie może osiągnąć wartości p/2, ponieważ wektor prądu jest zawsze przesunięty o kąt mocy ၪ względem wektora napięcia, a ၪ + ၤ = p/2. Wobec tego warunek maksymalizacji kąta ၤ sprowadza się do minimalizacji kąta ၪ:
, co oznacza pracę maszyny przy maksymalnym współczynniku mocy
. .

Uwzględniając, że na podstawie równania dla stanu ustalonego (ၷk = ၷs) oraz dla rs = 0, wektor strumienia skojarzonego z uzwojeniem stojana jest równy:
.

Wartość wskaźnika I2: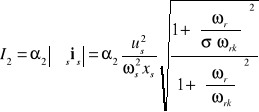
; gdzie: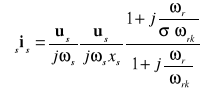
;

Minimalizacja I2 prowadzi do warunku:
, który oznacza on pracę SI z zachowaniem stałej pulsacji poślizgu wirnika
.

9. Podział układów regulacji momentu i prędkości silnika indukcyjnego

Moment można sterować przez:

- zmianę pulsacji poślizgu przy stałej amplitudzie strumienia skojarzonego wirnika,

- zmianę amplitudy strumienia wirnika przy zachowaniu stałej pulsacji poślizgu,

- kombinację obu wyżej wymienionych metod.

Dla sterowania ze stabilizacją strumienia Ψr=const oraz ze stabilizacją poślizgu ωr =const wyróżniamy metody:

- metody sterowania skalarnego - bierze pod uwagę zależności prawdziwe tylko w stanie ustalonym, czyli w układzie sterowania kontrolowane są tylko amplitudy i częstotliwości zmiennych stanu za pomocą amplitud wielkości sterujących (napięcia lub prądu stojana).

- metody sterowania wektorowego - oddziałuje się na wektory zmiennych stanu za pomocą wektorów wielkości sterujących - czyli w zamkniętych obwodach regulacji kontrolowane są nie tylko amplitudy i częstotliwości, ale i chwilowe położenia kątowe wektorów poszczególnych zmiennych stanu określających moment SI.

10. Wpływ rodzaju i orientacji sterowania na właściwości statyczne (charakterystyki mechaniczne) i dynamiczne (struktura sterowania momentem) silnika indukcyjnego

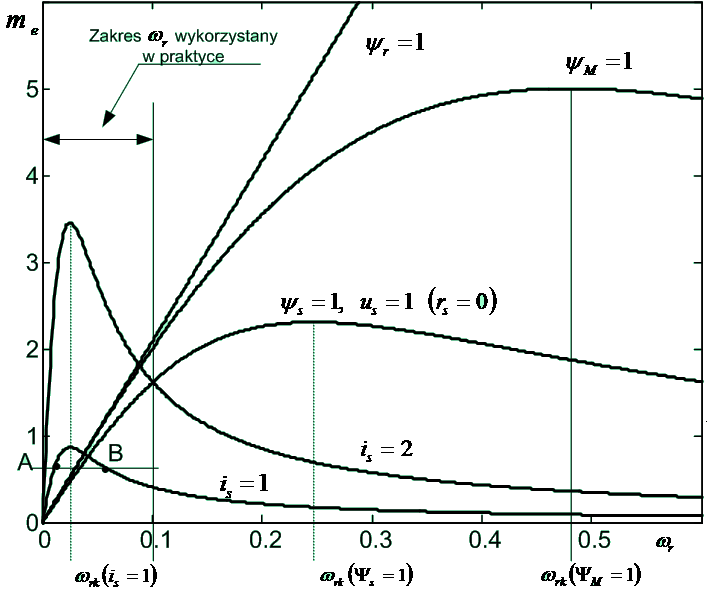
Ponieważ wektor elektromagnetycznych zmiennych stanu silnika można utworzyć za pomocą kombinacji dwu dowolnych wielkości elektromagnetycznych zmiennych stanu SI to na podstawie równań SI dla stanu ustalonego można moment wyrazić w funkcji amplitudy dowolnej zmiennej stanu lub zmiennej sterującej (np. amplitudy napięcia , prądu , strumienia stojana itd.). W związku z tym, można otrzymać nie tylko jedną zależność na charakterystykę mechaniczną silnika, ale również inne charakterystyki statyczne, odpowiadające innym zasadom sterowania momentem silnika indukcyjnego.

Przy pracy ze stałą amplitudą Ψr moment SI jest liniową funkcją częstotliwości względnej wirnika, wobec czego nie występuje tzw. utknięcie silnika, przy pozostałych rodzajach sterowania występuje wartość krytyczna momentu oraz odpowiadająca mu wartość poślizgu krytycznego (poślizg „utyku”). Poślizg krytyczny można wyznaczyć przyrównując do zera pochodną momentu względem poślizgu

11. Właściwości dynamiczne silnika indukcyjnego przy wymuszeniu prądu stojana w układzie polowo-zorientowanym; podobieństwo właściwości regulacyjnych SPS i SI sterowanego metodą polowo-zorientowaną

Silnik Indukcyjny przy wymuszeniu prądu stojana w układzie współrzędnych prostokątnych zorientowanym względem wektora strumienia wirnika, staje się liniowym obiektem sterowania. Strumień wirnika jest kształtowany z pomocą składowej isx wektora prądu stojana, natomiast moment dla stałej wartości strumienia wirnika zależy liniowo od składowej isy , zgodnie z wzorem:
; gdzie:
.

Analogia SPS i SI:

Wzór na moment SPS:
; Wzór na moment SI - sterowanego we współrzędnych polowych:

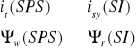
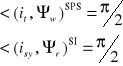
12. Porównanie struktury i właściwości dynamicznych układów pośredniego (Hasse) i bezpośredniego (Blaschke) sterowania polowo-zorientowanego

Podstawową cechą odróżniającą pośrednie IFOC od sterowania bezpośredniego DFOC jest inny sposób uzyskiwania informacji o aktualnym położeniu wektora strumienia wirnika.

W sterowaniu bezpośrednim informacja pochodzi z układu odtwarzającego składowe wektora strumienia wirnika na podstawie pomiaru prądów i napięć silnika - z estymatora tej zmiennej stanu. Bezpośrednie zadawanie składowej biernej isx wektora prądu stojana oraz inny sposób wyznaczania aktualnego położenia wektora strumienia wirnika eliminuje konieczność stosowania estymatorów strumienia. Jednak brak regulatora modułu wektora strumienia wirnika pogarsza nieco właściwości dynamiczne układu sterowania momentem silnika, w szczególności w strukturze z wymuszeniem napięciowym.

Natomiast w układzie sterowania pośredniego informacja ta uzyskiwana jest w wyniku zsumowania zmierzonej wartości prędkości wału i obliczonej wartości pulsacji poślizgu na podstawie wzoru i zadanych w układzie sterowania wartości składowych wektora prądu stojana. Charakterystyczne cechy metody:

- kąt położenia ၧsၹ wirującego układu współrzędnych (x-y) względem układu nieruchomego (ၡ-ၢ) nie jest mierzony lub obliczany bezpośrednio z informacji o wektorze strumienia, lecz uzyskiwany pośrednio, poprzez sumowanie mierzonego kąta położenia wirnika ၧm oraz kąta ၧrz, obliczanego na podstawie wartości zadanej isyz ,

- wynika z tego istotna wada metody, a mianowicie na dokładność wyznaczenia kąta położenia ၧsၹ będą miały wpływ takie parametry SI jak stała czasowa Tr obwodu wirnika oraz reaktancja główna xM.

13. Bezpośrednie sterowanie momentem SI

Kluczowym elementem metody DTC jest estymacja wektora strumienia skojarzonego stojana silnika. W celu wyestymowania wektora strumienia stojana należy znać wartość wektora napięcia stojana. Wektor napięcia stojana może zostać wyliczony na podstawie napięć zmierzonych na wyjściu falownika lub estymowany na podstawie stanu kluczy falownika. Metoda sterowania DTC jest: prosta w działaniu (co zwiększa jej niezawodność), niewrażliwa na zmiany parametrów silnika (poza rs ), nie wymaga trygonometrycznych przekształceń układu współrzędnych, nie wymaga stosowania regulatorów prądu.

Do charakterystycznych cech układu regulacji DTC należy zaliczyć:

- w przybliżeniu sinusoidalny kształt strumienia i prądu stojana;

- zawartość harmonicznych może być nastawiana przez zmianę wartości histerez regulatorów momentu i strumienia;

- możliwa jest praca wyłącznie z modulacją;

- częstotliwość łączeń nie jest stała i zależy od wartości napięcia zasilania, prędkości kątowej i parametrów silnika oraz szerokości histerez regulatorów momentu i strumienia;

- nie ma potrzeby stosowania osobnego bloku modulatora;

- nie są wymagane obwody bezpośredniej regulacji prądu;

- transformacja współrzędnych nie jest potrzebna;

- podobnie jak w systemach bezpośredniego sterowania polowo zorientowanego, jest wymagany pomiar lub estymacja wektora strumienia oraz momentu elektromagnetycznego silnika.

Cechy:

- możliwe sterowanie momentem bez zamkniętego toru regulacji prędkości

- moment sterowany „bezpośrednio”

Zalety

- bardzo szybka odpowiedź momentu

- pełny moment przy prędkości zero

- bardzo dokładne sterowanie prędkości

- niepotrzebny modulator

- uproszczenie struktury regulacji

14. Metody i układy skalarnego sterowania momentem i prędkością SI przy stabilizacji strumienia wirnika

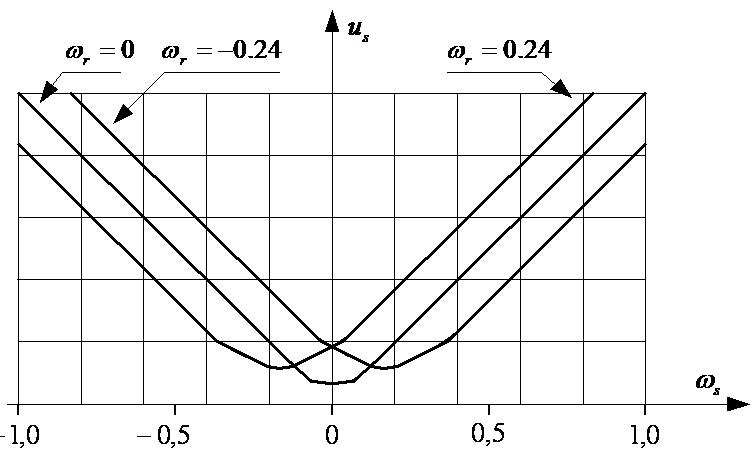
Pośrednia metoda sterowania amplitudy strumienia stojana przez zmianę amplitudy napięcia stojana;

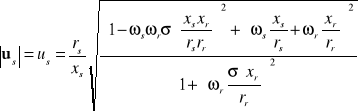
Charakterystyka sterowania:

- zapewnia korekcję amplitudy napięcia stojana o wartość spadku napięcia ၄us na rezystancji i reaktancji rozproszenia uzwojenia stojana w zakresie niskich wartości prędkości kątowej.

- realizowana jest kompensacja wpływu obciążenia silnik. Dąży się do tego, by poślizg ustalony nie przekraczał znamionowego.

Przy takim sposobie sterowania, wskutek zachowania w stanie ustalonym warunku stałej wartości strumienia, wartość momentu krytycznego również jest stała, co pociąga za sobą stałą przeciążalność momentem silnika.

Strumień stojana zachowuje stałą wartość w stanie ustalonym, co powoduje, że moment silnika jest proporcjonalny do częstotliwości poślizgu. W stanach dynamicznych strumień i moment silnika ulega zmianom wskutek zmian kąta obciążenia niekompensowanego w torze regulacji częstotliwości wirnika.

Pośrednia metoda sterowania amplitudy strumienia stojana lub wirnika przez zmianę amplitudy prądu stojana;

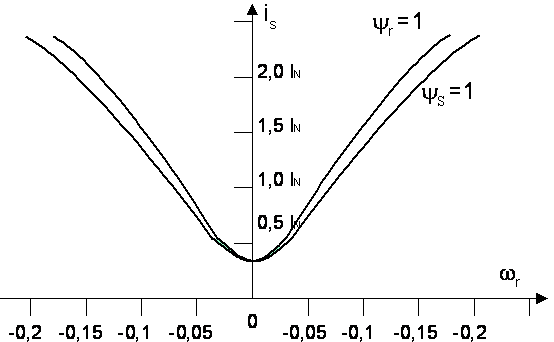
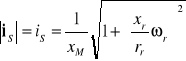
Właściwości metody:

- sumowanie częstotliwości kompensuje wpływ prędkości mechanicznej,

- w stanach ustalonych wielkość sterująca jest równa pulsacji poślizgu, gdyż wektory przestrzenne strumienia wirnika i prądu stojana wirują z jednakową prędkością, a kąt obciążenia pozostaje stały,

- sterowanie momentem silnika w stanach dynamicznych jest ograniczone, gdyż można nań wpływać jedynie za pomocą amplitudy prądu stojana

Bezpośrednia metoda sterowania amplitudy strumienia skojarzonego z uzwojeniem stojana (lub wirnika).

W metodzie tej wprowadza się do układu regulacji nadrzędny regulator strumienia RΨ, który zadaje amplitudę prądu silnika zapewniającą stałość strumienia w stanie ustalonym i zastępuje nieliniowy generator funkcji GNF z poprzedniej struktury.

W układzie wymagany jest pomiar amplitudy strumienia skojarzonego stojana lub wirnika, albo jego obliczenie na podstawie pomiaru napięcia czy prądy stojana. Charakterystyczne dla metody bezpośredniej stabilizacji strumienia jest to, że mimo stałej amplitudy strumienia nie można uzyskać szybkich zmian momentu, bo nie są kontrolowane zależności kątowe pomiędzy wektorami strumienia i prądu. Metoda ta nie przynosi żadnych korzyści dynamicznych, gdyż zmiana momentu przebiega bardzo wolno, co jest spowodowane, wolną zmianą kąta obciążenia.

15. Metody i układy sterowania momentem i prędkością SI przy stabilizacji częstotliwości względnej wirnika (poślizgu)

Metoda skalarna przy stabilizacji poślizgu ta opiera się na wzorze
określającym zależność momentu elektromagnetycznego silnika indukcyjnego od prądu stojana w stanie ustalonym, przy założeniu
. Sterowanie pulsacją poślizgu jest tu realizowane przy użyciu punktu sumowania częstotliwości. Właściwości tej metody:

- sumowanie częstotliwości
kompensuje wpływ prędkości mechanicznej, która stanowi sprzężenie wew. w silniku;

- w stanach ustalonych wielkość sterująca
jest równa pulsacji poślizgu
, gdyż
i kąt obciążenia pozostaje stały;

- w stanach przejściowych, wywołanych zmianami wielkości sterującej
, pulsacja poślizgu
w silniku różni się od wartości zadanej pulsacji poślizgu
, a różnica
wywołuje zmiany kąta obciążenia .

Metoda wektorowa przy stabilizacji poślizgu. Aby uzyskać dobre właściwości dynamiczne regulacji momentu silnika, nie wystarczy wykorzystać warunki stanu ustalonego i kontrolować w układzie sterowania tylko wielkości skalarne. Trzeba również, tak jak zawsze w przypadku sterowania wektorowego kontrolować zależności fazowe pomiędzy wektorami strumienia wirnika i prądu stojana - utrzymywać w stanach dynamicznych stały kąta obciążenia (równanie na „pulsacje i kąt”). Nadrzędny obwód regulacji momentu kompensuje nieliniową zależność między wartością zadaną momentu i prądu stojana, zapewniając liniowe charakterystyki statyczne układu. Dodatkowo regulator momentu redukuje zależność odpowiedzi czasowych od punktu pracy silnika. Dzięki temu, że regulator kąta obciążenia modyfikuje w stanach dynamicznych sygnał sterujący częstotliwością przemiennika , kąt obciążenia w silniku pozostaje stały.

Podsumowanie metod sterowania przy stabilizacji poślizgu:

- W wyniku zmian kąta obciążenia zarówno przebiegi amplitudy strumienia jak i momentu silnika są bardzo wolne oraz słabo tłumione.

- Odpowiedzi układu są zależne od punktu pracy silnika.

- Inercja jest wynikiem dużej stałej czasowej obwodu wirnika , która nie może być całkowicie skompensowana, gdyż amplituda będącego do dyspozycji prądu stojana jest w praktyce zawsze ograniczona.

- Aby zlikwidować słabo tłumione oscylacje, należy uwzględnić dodatkowo zależności fazowe, co ma miejsce w strukturze wektorowej ze stabilizacją kąta obciążenia .

16. Układy napędowe z silnikami bezszczotkowymi (BDCM) i z silnikami synchronicznymi z magnesami trwałymi (PMSM) - podstawowe struktury regulacji

Moment napędowy silnika SSMT:
. Moment ten osiąga maksymalna wartość dla

Równanie ruchu:

Budowa SMT (wyróżnia się dwie podstawowe konstrukcje):

- silnik z trapezoidalnym rozkładem SEM - BDCM

- silnik z sinusoidalnym przebiegiem SEM - PMSM

Cechy silnika z magnesami trwałymi

- mały moment bezwładności, małe stałe czasowe mechaniczne, duża przeciążalność momentem, rozwija moment obrotowy w czasie postoju, szeroki zakres regulacji prędkości,

Budowa wirnika silnika z magnesami trwałymi

- magnesy naklejane na powierzchni walcowego rdzenia,

- umieszczone w rdzeniu, mocowane tuleją ze stali niemagnetycznej,

- patent Parvex Francja,

- magnesy zagłębione w rdzeniu wirnika,

Struktury regulacji SSMT

- Sterowanie wektorowe - z regulatorami PI prądu. (Zaleta: dokładność regulacji prądu, doskonała dynamika)

- Sterowanie wektorowe z regulatorami histerezowymi (dokładność zależy od szerokości pętli histerezy, punktu pracy serwonapędu)

- Struktura sterowania typu „sensorless” (bez pomiaru prędkości i położenia)

- Struktura z rozmytą regulacjąprędkości i położenia (jedna z metod sterowania odpornego, nie wymaga znajomości modelu matematycznego, wymagana wiedza ekspercka)

Silniki PMSM warto stosować wszędzie tam, gdzie:

- wymagane są wysokie parametry dokładnościowe, dobra dynamika,

- uzasadnia to koszt ekonomiczny

- optymalne właściwości dynamiczne sterowania momentem - przy sterowaniu wektorowym

9

---