PROGNOZOWANIE NA PODSTAWIE KLASYCZNYCH MODELI TRENDU

W przypadku, gdy zjawisko jest opisane za pomocą trendu oraz wahań przypadkowych, wówczas można zastosować klasyczne modele trendu. W praktyce szereg powinien składać się z co najmniej 9-11 wyrazów. Ogólna postać modelu przyjmuje postać

lub
,

gdzie:

- poziom zjawiska w okresie t,

- poziom zjawiska w okresie t oszacowany na podstawie funkcji tendencji rozwojowej (trendu),

- składnik resztowy modelu, zwany składnikiem nieregularnym.

Do najczęściej stosowanych klasycznych modeli trendu zalicza się następujące:

• trend liniowy,

• trend wykładniczy,

• trend wielomianowy stopnia drugiego,

• trend wielomianowy stopnia trzeciego,

• trend potęgowy,

• trendy hiperboliczne.

Przykładowe wykresy trendów:

• liniowy (
  ),

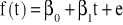
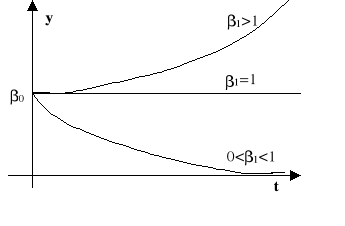
• wykładniczy (
  ),

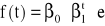
• wielomianowy stopnia drugiego (
  ),

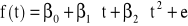
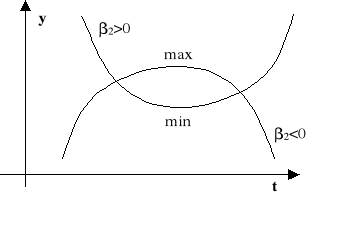
• potęgowy (
  ).

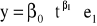
W celu ustalenia postaci analitycznej równania modelu można wykorzystać:

• aprioryczną wiedzę merytoryczną o badanych zależnościach (np. z teorii ekonomii wynika, że do konstrukcji modeli opisujących kształtowanie się produkcji w zależności od czynników produkcji wykorzystuje się najczęściej modele potęgowe),

• ocenę wzrokową rozrzutu punktów empirycznych na wykresach korelacyjnych. To podejście może być stosowane tylko i wyłącznie przy budowie modelu z jedną zmienną objaśniającą,

• podejście heurystyczne oparte o metodę prób i błędów polegające na szacowaniu dla tego samego zbioru danych modeli o różnych analitycznych postaciach i wyborze spośród nich tego, który najlepiej opisuje badane zjawisko. Każdy oszacowany model poddajemy weryfikacji merytoryczno-statystycznej i wybieramy ten, który ma najlepsze własności.

Przy budowie modelu przeprowadzamy dwa rodzaje weryfikacji:

1. Weryfikację merytoryczną polegającą na sprawdzeniu czy otrzymane wartości ocen parametrów strukturalnych są zgodne ze zdrowym rozsądkiem i z intuicją badającego. W szczególności należy sprawdzić sensowność znaków ocen parametrów strukturalnych modelu.

2. Weryfikację statystyczną polegającą na sprawdzeniu, czy model z dostateczną dokładnością odzwierciedla badany fragment rzeczywistości gospodarczej poprzez określenie:

• stopnia wyjaśnienia danego zjawiska poprzez zmienne objaśniające,

• stopnia dopasowania modelu do danych empirycznych,

• błędów szacunku parametrów strukturalnych modelu,

• istotności parametrów strukturalnych modelu.

Weryfikację statystyczną przeprowadza się na podstawie następujących analiz:

• analizy wariancji zmiennej objaśnianej,

• analizy ocen parametrów struktury stochastycznej modelu. W tym celu stosujemy następujące mierniki:

• odchylenie standardowe składnika losowego,

• współczynnik zmienności składnika losowego inaczej zwany współczynnikiem wyrazistości,

• błędy średnie szacunku ocen parametrów strukturalnych,

• współczynnik determinacji, współczynnik rozbieżności, skorygowany współczynnik determinacji,

• wartości empiryczne statystyki F w odniesieniu do wszystkich ocen parametrów strukturalnych badanego modelu oraz t-Studenta do poszczególnych ocen parametrów strukturalnych.

Zalety jakie ma stosowanie klasycznych modeli trendu do prognozowania:

• do budowy modelu tendencji rozwojowej niezbędne są jedynie dane empiryczne odnoszące się do zmiennej prognozowanej, która jest zmienną objaśnianą,

• nie występuje kłopotliwy problem znajomości wartości zmiennych objaśniających w okresie prognozowanym, należy tylko ustalić wartość zmiennej czasowej w przyszłości,

• parametry modeli tendencji rozwojowej można łatwo oszacować, gdyż są to najczęściej modele liniowe lub dające się do takich sprowadzić (wykładnicze, wielomianowe, potęgowe),

• stosunkowo łatwo można także ocenić dokładność budowanych prognoz, wykorzystując mierniki dokładności prognoz ex ante, które są obliczane jednocześnie z prognozą.

Trudności jakie mają miejsce w trakcie budowy prognoz na podstawie modeli tendencji rozwojowej:

• musi być zachowana zasada zwana dynamiczne status quo, orzekająca że w przyszłości na zmienną prognozowaną będą oddziaływać niezmiennie te same co dotychczas czynniki, to oznacza, że prognosta powinien być przekonany, że wykryta prawidłowość jest niezmienna w czasie lub prawie niezmienna w czasie, że zjawisko charakteryzuje się dużą inercją.

PROGNOZOWANIE NA PODSTAWIE ADAPTACYJNYCH MODELI TRENDU

Adaptacyjne modele trendu - są to modele, przy konstrukcji których odrzuca się krępujące założenie o niezmienności mechanizmu rozwojowego badanych zjawisk w przyszłości, co oznacza, że przy budowie tych modeli nie zakłada się stałości postaci analitycznej funkcji trendu i dopuszcza się możliwość zmian parametrów strukturalnych modelu w czasie. Modele mają dużą elastyczność i zdolność dostosowawczą w przypadku nieregularnych zmian kierunku lub szybkości trendu, czy też przesunięć i zniekształceń wahań periodycznych, gdy przebieg zjawiska w czasie nie jest dostatecznie stabilny. Modele adaptacyjne stosujemy jako narzędzie prognoz krótkookresowych. Wśród adaptacyjnych metod prognozowania wyróżniamy trzy podstawowe metody:

• średnich ruchomych,

• wyrównywania wykładniczego,

• trendu pełzającego i wag harmonicznych.

Metoda średnich ruchomych (metoda mechaniczna) polega na zastąpieniu pierwotnych wartości zmiennej prognozowanej średnimi arytmetycznymi (prostymi lub ważonymi), obliczanymi sekwencyjnie dla wybranej liczby obserwacji - liczby wyrazów średniej ruchomej, zwanej stałą wygładzania (k), którą określa prognosta. Średnia ruchoma wyznaczona z większej liczby wyrazów silniej wygładza szereg. Wyznaczone wartości średnie przypisuje się na ogół środkowym obserwacjom, na podstawie których były obliczane średnie, niekiedy przypisuje się je obserwacjom ostatnim. Z kolei średnia arytmetyczna ważona przypisuje różne znaczenie obserwacjom z różnych okresów. Podstawowym problemem w tej metodzie jest ustalenie tych wag, jak i stałej wygładzania. Do wyznaczenia liczby wyrazów średniej ruchomej można użyć średniego kwadratowego błędu prognozy ex post - wyrażającego w tym przypadku odchylenia prognoz wygasłych od wartości zmiennej prognozowanej:

,

gdzie:

- prognoza zmiennej Y wyznaczona na moment lub okres t,

- wartość zmiennej prognozowanej w momencie lub okresie t,

n - liczba wyrazów szeregu czasowego zmiennej prognozowanej,

k - stała wygładzania.

Spośród różnych, wstępnie przyjętych wartości stałej
, jako ostateczną wybiera się tę, dla której wielkość błędu jest najmniejsza.

Metody średnich ruchomych stosuje się na ogół do prognozowania, gdy:

• poziom wartości zmiennej prognozowanej jest prawie stały w rozpatrywanym okresie, z niewielkimi odchyleniami losowymi,

• w szeregu czasowym nie występują: tendencja rozwojowa i wahania sezonowe oraz cykliczne.

Używając modeli średniej ruchomej do prognozowania, przyjmuje się, że wartość zmiennej prognozowanej w następnym momencie lub okresie będzie równa średniej arytmetycznej (prostej lub ważonej) z k ostatnich wartości tej zmiennej. W przypadku średniej arytmetycznej formuła takiej prognozy jest następująca:

,

gdzie:

- prognoza zmiennej Y wyznaczona na moment lub okres t,

- wartość zmiennej prognozowanej w momencie lub okresie
,

- stała wygładzania (określana przez prognostę).

Wada modelu średniej ruchomej prostej - nadawanie tych samych wag (jednostkowych) wszystkim
 wartościom zmiennej prognozowanej, na których podstawie wyznacza się prognozę (nowsze dane zawierają bardziej aktualne informacje o prognozowanym zjawisku, zatem powinny być im nadawane relatywnie większe wagi niż obserwacjom starszym - postulat postarzania informacji).

Z kolei rozpatrując średnią ważoną otrzymujemy wzór o postaci

gdzie:

- waga nadana przez prognostę wartości zmiennej prognozowanej w momencie lub okresie
(
oraz
).

Def. 1. Układ liczb
nieujemnych i sumujących się do stałej
nazywamy wagami nieunormowanymi.

Def. 2. Układ liczb
nieujemnych i sumujących się do jedności nazywamy wagami unormowanymi.

Wybrane typy wag:

• ważenie w sposób potęgowy,

, czyli

,
, ...,
,
,

• ważenie w sposób liniowy

, zatem

,
, ...,
,
.

Uwagi końcowe !

1. Modele średniej ruchomej stosuje się na ogół do prognozowania, gdy:

• poziom wartości zmiennej prognozowanej jest prawie stały w rozpatrywanym okresie, z niewielkimi odchyleniami losowymi,

• w szeregu czasowym nie występują: tendencja rozwojowa i wahania sezonowe oraz cykliczne.

2. Do oceny dopuszczalności prognozy można użyć np. średniego kwadratowego błędu prognozy ex post.

3. W razie pojawienia się w szeregu czasowym liniowej tendencji rozwojowej, konstruujemy tzw. model podwójnej średniej ruchomej - wygładzony (średnią ruchomą prostą lub ważoną) szereg wartości zmiennej prognozowanej poddaje się powtórnemu wygładzeniu metoda średniej ruchomej.

4. Przy konstrukcji prognozy na podstawie modeli średniej ruchomej uwzględnia się jedynie
ostatnich wartości zmiennej prognozowanej. Nie uwzględnia się (z wyjątkiem przypadku, gdy
) obserwacji pochodzących z momentów lub okresów wcześniejszych od
, które także dostarczają pewnych informacji dotyczących kształtowania się wartości zmiennej prognozowanej w przeszłości.

5. Jeszcze jedną wadą tych modeli jest potrzeba, przy dużej wartości parametru
, przechowywania dużej niekiedy liczby danych. W praktyce najmniejsze błędy prognoz daje średnia z 12 i więcej obserwacji.

6. Przy korzystaniu z tych modeli nie bierze się pod uwagę związków przyczynowych, w które uwikłane są prognozowane zmienne.

7. Model średniej ruchomej należy do grupy tzw. modeli naiwnych. Może być stosowany do przewidywania sprzedaży, dochodów, przepływów gotówkowych itp. wielkości, nawet bez potrzeby użycia komputera.

Metoda wygładzania (wyrównywania) wykładniczego. Istota tej metody polega na tym, że szereg czasowy zmiennej prognozowanej wygładza się za pomocą ważonej średniej ruchomej, przy czym wagi są określane według funkcji wykładniczej. Podstawowym założeniem przy stosowaniu tych metod jest przyjęcie, że przyrosty wartości trendu zmiennej prognozowanej (poza okresami, kiedy następowała zmiana lub załamanie trendu) są w przybliżeniu stałe lub zmieniają się w regularny sposób.

Model wyrównania wykładniczego Browna rzędu pierwszego

Procedura wyrównania wykładniczego Browna rzędu pierwszego umożliwia otrzymanie prognozy przez wykładnicze ważenie przyszłych wartości szeregu. Stosuje się ten model w przypadku występowania wahań przypadkowych, czyli szeregu czasowego bez wyraźnie zaznaczonego trendu. Prognozę uzyskuje się z następującego wzoru:

,

gdzie:

- prognoza dla okresu t (
),

- poziom zmiennej prognozowanej w okresie
,

- prognoza dla okresu
sporządzona w okresie
,

α - stała wyrównania
.

Wartość początkową prognozy
można wyznaczyć jednym ze sposobów m. in.: jako średnia z kilku pierwszych okresów, metodą prognozowania „wstecz”, metodą najmniejszych kwadratów, albo przez przyjęcie wartości
.

Model wyrównania wykładniczego Browna rzędu drugiego

Procedura wyrównania wykładniczego Browna rzędu drugiego polega na podwójnym wygładzaniu rzeczywistych wartości Y. Model ten znajduje zastosowanie w przypadku szeregu czasowego wykazującego trend liniowy. Dany szereg czasowy wygładza się zgodnie ze wzorem:

,

a następnie wygładza się wartości prognoz
:

Wówczas prognozę w okresie t dla p okresów określa się następująco:

,

gdzie:
- ocena poziomu trendu w okresie t,

- ocena zmian trendu w okresie t.

W metodzie wygładzania wykładniczego ważny jest wybór wartości początkowej w wygładzonych szeregach i stałej wygładzania
. Najczęściej przyjmuje się jako wartość początkową
oraz
.

Model wyrównania wykładniczego Browna rzędu trzeciego

Procedura wyrównania wykładniczego Browna rzędu trzeciego polega na potrójnym wygładzaniu rzeczywistych wartości
. Model ten znajduje zastosowanie w przypadku występowania w szeregu czasowym trendu nieliniowego (wielomianowego stopnia drugiego). Dany szereg czasowy wygładza się zgodnie ze wzorami

,

,

.

Prognozę dla p okresów sporządza się na podstawie wzoru:

,

gdzie:
,

,

.

Najczęściej przyjmuje się jako wartość początkową
.

Model wyrównania liniowo-wykładniczego Holta

Procedura wyrównania liniowo-wykładniczego Holta służy do wygładzania poziomu trendu według wzoru:

,

a następnie do wygładzania zmian trendu:

.

Wówczas prognoza w okresie t dla p okresów jest następująca:

.

Model ten znajduje zastosowanie dla szeregu czasowego bez wahań sezonowych. Za wartość początkową
i
można przyjąć - odpowiednio - wyraz wolny i wyraz nachylenia trendu liniowego.

Metoda trendu pełzającego i wag harmonicznych. W metodzie tej uwzględnia się postulat głoszący, że wpływ nowszych danych na wartość prognozy powinien być większy od wpływu danych starszych i wykorzystuje się do wyznaczania prognoz zjawisk, które charakteryzują się nieregularnością i załamaniami trendu.

Prognozowanie tą metodą składa się z następujących części:

1. metody wyrównania szeregu czasowego za pomocą trendu pełzającego,

2. metody szacowania przyszłego prawdopodobnego kształtowania się zjawiska za pomocą wag harmonicznych.

Metoda trendu pełzającego. Wygładzanie szeregu czasowego opartego na funkcjach segmentowych, może odbywać się przy stałej lub zmiennej długości segmentu. Dla szeregu czasowego ze stałym segmentem wygładzania szacuje się parametry liniowych funkcji trendu na podstawie kolejnych fragmentów szeregu:

,

,

..........................

,

gdzie L - oznacza długość segmentu. W ten sposób otrzymujemy
liniowych trendów ruchomych. Na ich podstawie dla kolejnych okresów lub momentów t = 1, 2, ..., n dostaje się j = 1, 2, ..., 
wartości teoretycznych dla i-tego segmentu
, które wygładza się za pomocą średnich:

.

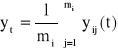
Prognoza metodą wag harmonicznych. Obliczony trend pełzający jest punktem wyjścia do oszacowania prognozy. Wówczas konstruujemy prognozę w następujących krokach:

1. wyznaczamy przyrosty funkcji trendu

dla t = 1, 2, ..., n-1,

2. obliczamy średnią przyrostu

,

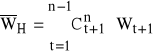
gdzie
- odpowiednio dobrane wartości współczynnika zwanego wagą harmoniczną i spełniającego warunki:
(dla t = 1, 2, ..., n-1) i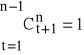
.

Jedna z metod ustalania wag przyjmuje postulaty:

1. informacje pochodzące z okresów dawniejszych powinny mieć wagę mniejszą od informacji aktualnych,

2. przyrosty wag powinny być odwrotnie proporcjonalne do czasu, jaki dzieli daną informację od informacji najświeższej.

Wagi mają postać:

dla t = 1, 2, ..., n-1.

Prognozę wyznacza się dodając do ostatniego wyrazu trendu wartość średniego przyrostu, czyli

dla t > n.

PROGNOZOWANIE ZJAWISK GOSPODARCZYCH

Z UWZGLĘDNIENIEM WAHAŃ SEZONOWYCH

Kształtowanie się określonego zjawiska w czasie może być przedstawione za pomocą modeli składowych szeregu czasowego. W praktyce stosuje się dwie formuły dekompozycji zaobserwowanych wartości szeregu czasowego. Pierwsza zakłada stosowanie modelu addytywnego składowych szeregu czasowego, co zapisujemy następująco:
,

druga oparta jest natomiast na modelu multiplikatywnym:
,

gdzie:

- poziom zjawiska w okresie t,

- poziom zjawiska w okresie t oszacowany na podstawie funkcji tendencji rozwojowej (trendu),

- wahania sezonowe w okresie t, przy czym
oznacza liczbę podokresów cyklu okresowości,

- składnik resztowy modelu, zwany składnikiem nieregularnym.

Funkcje tendencji rozwojowych
przedstawiają rozwój zjawiska w czasie, jego regularne i systematyczne zmiany w ciągu długiego okresu (np. tendencję rozwojową targowiskowych cen zbóż w Polsce w latach 1995-2006).

Wahania sezonowe
są to zmiany, które powtarzają się regularnie w tym samym okresie każdego roku. Przykładowo, na wahanie zjawisk gospodarczych w rolnictwie mają wpływ różne czynniki natury biologiczno-technicznej oraz klimatyczne, które powtarzają się w określonych porach roku (sezonach).

Wahania przypadkowe
, zwane nieregularnymi lub losowymi, wynikają z oddziaływania na dane zjawisko czynników nie dających się przewidzieć (np. wpływu czynników klimatyczno-biologicznych - powodzi, pożarów, gradobicia - na wyniki produkcyjne i ekonomiczne rolnictwa, wpływu zmian polityki rządu na ceny produktów rolnych itd.).

Procedura konstrukcji prognozy z uwzględnieniem wahań sezonowych przebiega następująco:

1) WYKRYWANIE WAHAŃ SEZONOWYCH

Występowanie wahań sezonowych w analizowanym zjawisku można określić na podstawie:

• pozastatystycznej wiedzy o danym zjawisku,

• analizy graficznej,

• analizy statystycznej.

Analiza graficzna polega na sporządzeniu dwóch wykresów, na których przedstawiamy:

• poziom danego zjawiska dla analizowanego szeregu czasowego,

• poziom danego zjawiska dla jednoimiennych okresów (np. kwartałów lub miesięcy).

Jeśli wahania dla okresów jednoimiennych są dużo mniejsze od wahań dla całego szeregu czasowego, to wówczas stwierdzamy istnienie w szeregu wahań sezonowych.

Analiza statystyczna polega na stosowaniu odpowiednich testów statystycznych np. nieparametrycznego testu zwanego testem sum rang (test Kruskala-Wallisa). Jeśli wahania mają charakter przypadkowy (bez sezonowości), to rozkład tych wahań powinien być taki sam we wszystkich okresach.

W celu sprawdzenia istotności wahań sezonowych stosujemy nieparametryczny test zwanym testem sum rang (test Kruskala-Wallisa).

Wówczas statystyka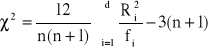
ma rozkład chi-kwadrat o
stopniach swobody, gdzie:
- liczba podokresów cyklu okresowości,
- liczba efektów sezonowych
,

- liczba efektów sezonowych w i-tym podokresie, R_i - suma rang w i-tym podokresie.

2. WYODRĘBNIANIE TENDENCJI ROZWOJOWEJ badanego zjawiska z szeregu czasowego stosując:

1. Metodę analityczną, która polega na dopasowaniu do danych empirycznych (całego szeregu czasowego) odpowiedniej funkcji trendu (np. funkcji trendu liniowego
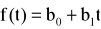
   ) i wyznaczeniu wartości teoretycznej dla każdego okresu (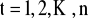
   ).

2. Metodę mechaniczną, która polega na obliczeniu średnich ruchomych lub średnich ruchomych scentrowanych
   .

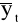
Średnia ruchoma 4-okresowa (dla danych w układzie kwartalnym):

Średnia ruchoma 12-okresowa (dla danych w układzie miesięcznym):

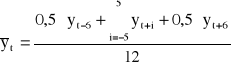
3. ELIMINACJA TENDENCJI ROZWOJOWEJ Z SZEREGU CZASOWEGO. W przypadku stosowania modelu addytywnego eliminacji tej dokonuje się obliczając różnice zaobserwowanych wartości cechy
od wartości teoretycznych - obliczonych
lub
:

lub
.

Natomiast w przypadku modelu multiplikatywnego wyznaczamy ilorazy:

lub
.

Obliczone wielkości
zawierają wahania sezonowe i przypadkowe.

4. ELIMINACJA WAHAŃ PRZYPADKOWYCH poprzez obliczenie tzw. surowych wskaźników sezonowości. Stanowią je średnie arytmetyczne dla okresów jednoimiennych, czyli
dla i-tego podokresu cyklu okresowości (
), natomiast m jest liczbą lat badania sezonowości (np. gdy podokresami są kwartały mamy
,
,
,
). Suma wartości surowych wskaźników sezonowości jest różna od zera (
) dla modelu addytywnego, natomiast różna od liczby rozpatrywanych podokresów d (
) dla modelu multiplikatywnego.

5. WYZNACZANIE WSPÓŁCZYNNIKA KOREKTY

i na tej podstawie wartości OCZYSZCZONYCH WSKAŹNIKÓW SEZONOWOŚCI:

1. dla modelu addytywnego - odejmując od poszczególnych wartości surowych wskaźników sezonowości współczynnik korekty K:

dla
, przy czym
.

2. dla modelu multiplikatywnego - dzieląc wartości surowych wskaźników sezonowości przez współczynnik korekty K:

dla
, przy czym
.

Wartości oczyszczonych wskaźników sezonowości
(
) informują, o ile jednostek bezwzględnych wartości cechy obserwowane w i-tym podokresie cyklu są (na skutek wahań sezonowych) wyższe (
) lub niższe (
) od przeciętnej podokresu (model addytywny). W przypadku modelu multiplikatywnego wartości
określają, o ile procent wartości cechy obserwowane w i-tym podokresie cyklu są (na skutek wahań sezonowych) wyższe lub niższe od przeciętnej podokresu (100%).

6. ELIMINACJA SEZONOWOŚCI Z SZEREGU CZASOWEGO

Po wyznaczeniu oczyszczonych wskaźników sezonowości usuwamy je z analizowanego zjawiska poprzez:

• ich odjęcie - dla modelu addytywnego
  ,

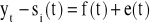
• ich podzielenie - dla modelu multiplikatywnego
  .

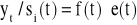
7. WYODRĘBNIENIE TENDENCJI ROZWOJOWEJ

Otrzymany szereg czasowy po wyeliminowaniu efektów wahań sezonowych służy do wyznaczania tendencji rozwojowej badanego zjawiska (w punkcie 6 otrzymaliśmy funkcje trendu
oraz wahania przypadkowe
).

8. SZACOWANIE WAHAŃ PRZYPADKOWYCH

Po wyeliminowaniu sezonowości (punkt 6) usuwamy tendencję rozwojową zjawiska otrzymując wahania przypadkowe poprzez:

• ich odjęcie - dla modelu addytywnego
  ,

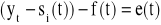
• ich podzielenie - dla modelu multiplikatywnego
  .

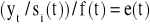
9. BUDOWA PROGNOZY

Prognozę buduje się korzystając z funkcji trendu, a następnie uwzględnia się wskaźniki sezonowości:

• dla modelu addytywnego
  ,

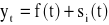
• dla modelu multiplikatywnego
  .

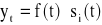
MODEL WYRÓWNANIA WYKŁADNICZEGO WINTERSA

Model wyrównania wykładniczego Wintersa jako adaptacyjny model trendu może być stosowany do szeregu czasowego, w którym występują wahania sezonowe. Niezależnie od tego, czy model jest addytywny czy multiplikatywny, występują następujące parametry: α - stała wygładzania dla poziomu trendu, γ - stała wygładzania dla zmian trendu, δ - stała wygładzania dla wahań sezonowych.

Rozpoczęcie wyrównywania szeregu czasowego metodą Wintersa wymaga obliczenia wartości początkowych, czyli oceny funkcji trendu
w okresie
, oceny zmian trendu
w okresie
i oczyszczonych wskaźników wahań sezonowych
dla i-tego okresu jednoimiennego (np. miesiąca lub kwartału). W celu określenia wielkości
,
,
dokonuje się arbitralnego podziału szeregu czasowego o n jednostkach na dwa szeregi czasowe odpowiednio o
i
jednostkach, przy czym
. Na podstawie danych z pierwszego szeregu uzyskuje się informacje o rozważanych wielkościach. Natomiast z drugiego szeregu otrzymuje się wyrównane wartości badanej cechy oraz jej prognozy na kolejne okresy czasowe. Dla modelu addytywnego o postaci:

,

wygładzanie prowadzi się w oparciu o następujące równania:

,

,

gdzie:
- przebiega przez kolejne okresy jednoimienne (
),

- liczba wyodrębnionych okresów jednoimiennych,

- ocena trendu w okresie t dla danych po wyeliminowaniu sezonowości,

- wygładzone wskaźniki sezonowości w i-tym okresie jednoimiennym.

Prognozę w okresie t dla p okresów buduje się według wzoru:

Dla modelu multiplikatywnego o postaci
,

podstawą są następujące równania:

,

,

.

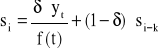
Prognozę w okresie t dla p okresów buduje się według wzoru:
.

Do budowy prognozy na podstawie szeregu czasowego z wahaniami sezonowymi można zastosować autoregresyjne modele wahań sezonowych lub metodę trendów jednoimiennych.

PROGNOZOWANIE ZJAWISK GOSPODARCZYCH

Z UWZGLĘDNIENIEM WAHAŃ SEZONOWYCH I CYKLICZNYCH

Jeśli wstępna analiza materiału empirycznego wykazuje istnienie wahań cyklicznych tj. zmian powtarzających się regularnie w okresie zdecydowanie dłuższym od rocznego (np. cykl świński trwa 3-4 lata), to szereg czasowy można opisać modelem:

1. addytywnym
   ,

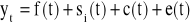
2. multiplikatywnym
   .

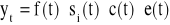
gdzie:

- poziom zjawiska w okresie t,

- poziom zjawiska w okresie t oszacowany na podstawie funkcji tendencji rozwojowej (trendu),

- wahania sezonowe w okresie t, przy czym
oznacza liczbę podokresów cyklu okresowości,

- wahania cykliczne w okresie t,

- składnik resztowy modelu, zwany składnikiem nieregularnym.

Procedura konstrukcji prognozy z uwzględnieniem wahań cyklicznych i sezonowych na przykładzie modelu multiplikatywnego przebiega następująco:

1. WYZNACZENIE TRENDU I WAHAŃ CYKLICZNYCH. W tym celu oblicza się średnią ruchomą (przy nieparzystej liczbie okresów) lub średnią ruchomą scentrowaną (przy parzystej liczbie okresów), która reprezentuje tendencję rozwojową
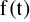
   i wahania cykliczne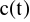
   .

2. ELIMINACJA TENDENCJI ROZWOJOWEJ I CYKLICZNOŚCI Z SZEREGU CZASOWEGO. W przypadku modelu multiplikatywnego oblicza się ilorazy (obliczone wielkości
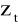
   zawierają wahania sezonowe i przypadkowe)

3. OBLICZENIE OCZYSZCZONYCH WSKAŹNIKÓW SEZONOWOŚCI. W celu wyeliminowania wahań przypadkowych z wielkości
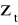
   wyznacza się tzw. surowe wskaźniki sezonowości, które poddaje się oczyszczeniu dzieląc je przez współczynnik korekty K.

4. ELIMINACJA SEZONOWOŚCI Z SZEREGU CZASOWEGO polega na podzieleniu wartości badanego zjawiska w okresie t przez odpowiedni oczyszczony wskaźnik sezonowości

5. OSZACOWANIE TENDENCJI ROZWOJOWEJ z szeregu czasowego po usunięciu sezonowości,

6. WYODRĘBNIENIE WAHAŃ CYKLICZNYCH dzieląc średnią ruchomą (lub średnią ruchomą scentrowaną) przez funkcję trendu

7. OBLICZENIE WAHAŃ PRZYPADKOWYCH jako iloraz wartości analizowanego zjawiska po usunięciu sezonowości przez średnią ruchomą (lub scentrowaną)

8. KONSTRUKCJA PROGNOZY. Prognozę buduje się korzystając z funkcji trendu i oczyszczonych wskaźników sezonowości, a następnie uwzględnia się wahania cykliczne:

OCENA TRAFNOŚCI PROGNOZ

Do oceny trafności prognoz można wykorzystać następujące mierniki błędów prognoz ex post:

• błąd średni
  ,

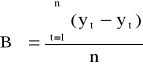
• średni błąd bezwzględny
  ,

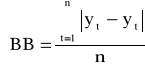
• średni błąd procentowy
  ,

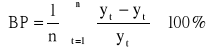
• średni bezwzględny błąd procentowy
  .

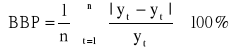
Błąd średni i średni błąd bezwzględny opierają się na uśrednieniu odpowiednio różnicy lub bezwzględnej różnicy pomiędzy rzeczywistą wartością analizowanego zjawiska a jego wartością prognozowaną. Błędy te wyrażają się w jednostkach naturalnych. Im ich wartości są bliższe zera tym prognoza jest doskonalsza. Natomiast średni błąd procentowy i średni bezwzględny błąd procentowy wyrażają względne odchylenia prognoz od wartości rzeczywistych, tzn. w stosunku do wielkości rzeczywistych. Określają one miarę względnego całkowitego dopasowania.

Na podstawie mierników prognoz ex post można przyjąć, że skonstruowane prognozy są bardzo dobre dla miernika ≤ 3%, prognozy są dobre dla 3% < miernika ≤:5%, prognozy są dopuszczalne dla 5% < miernika ≤ 10% oraz prognozy są niedopuszczalne dla miernika > 10%.

Literatura

Prognozowanie gospodarcze. Metody i zastosowania. Red. naukowa Maria Cieślak, PWN, Warszawa 1997.

Stańko S. (1999): Prognozowanie w rolnictwie, Wydawnictwo SGGW, Warszawa.

Zeliaś A. (1997): Teoria prognozy. PWE, Warszawa.

Zeliaś A., Pawełek B., Wanat S. (2003): Prognozowanie ekonomiczne. Teoria przykłady zadania. PWN, Warszawa.

Modele, w których zmienność zmiennej objaśnianej - prognozowanej jest opisywana tylko przez jedną specyficzną zmienną objaśniającą, jaką jest czas.

Sezonowość produkcji rolniczej wpływa na rynek rolny, dochody rolnicze i nakłady, od niej uzależniona jest podaż produktów rolniczych i poziom cen.

---