Laboratorium z fizyki

Sprawozdanie z ćwiczenia nr 3

Temat: ”Pomiar prędkości dźwięku w powietrzu metodą składania drgań elektrycznych”

Wykonał:

Paweł Waskian

I Elektronika

Grupa laboratoryjna nr 3

1) Cel ćwiczenia

Celem ćwiczenia jest wyznaczenie prędkości rozchodzenia się fal dźwiękowych w powietrzu w zależności od ich częstości.

2) Część teoretyczna

Źródłem dźwięku jest każde urządzenie, które drgając powoduje okresowy ruch powietrza. Jeżeli ruch te jest przez dłuższy czas okresowy odbieramy wrażenie słuchowe zwane dźwiękiem, w granicach częstotliwości od 16 do 20000 Hz . Drgania o wyższej częstotliwości nazywamy ultra dźwiękami, a o niższej infradźwiękami. Źródło dźwięku drgające z częstotliwością „słyszaną” znajdujące się w ośrodku sprężystym stałym, ciekłym lub gazowym wzbudza w nim fale głosowe.

Jest to fala przemieszczeń cząsteczek prowadząca do wytworzenia się zagęszczeń i rozrzedzeń lub też falę zmian ciśnień.

Ruch falowy

Zjawisko rozprzestrzeniania się drgań w środowisku sprężystym nazywamy falą. Każda z cząsteczek w tym procesie drga wokół własnego położenia równowagi

Rozchodzenie się drgań

Rozpatrzmy zjawisko rozchodzenia się drgań wzdłuż prostej OX , gdzie dana cząsteczka rozpocznie drganie w początku tego układu w chwili t = 0 w kierunku osi OY zgodnie z zależnością:

gdzie: y₀ - wychylenie z położenia równowagi w punkcie 0

a - amplituda wychylenia

- prędkość kątowa

t - czas

Jeżeli chcemy dowiedzieć się po jakim czasie drgania dojdą do punktu P znajdującego się w dowolnym miejscu osi OX to musimy skorzystać ze wzoru:

gdzie: X - odległość punktu P od początku układu współrzędnych

V - prędkość rozchodzeni się fali

Jeżeli wiemy, że od momentu rozpoczęcia drgań w punkcie 0 upłynął czas t , to od momentu rozpoczęci ich w punkcie P upłynął czas . Tak więc wychylenie cząsteczki w punkcie P można zapisać równaniem:

Powyższe równanie jest równaniem fali płaskiej rozchodzącej się w kierunku OX. Podaje ono wychylenie z położenia równowagi w dany punkcie odległym od źródła drgań o X po czasie t.

Z rysunku przedstawiającego rozchodzenie się drgań wynika, że fazy różnych punktów w tym samym momencie czasu są różne. Odległości między sąsiednimi punktami drgającymi w zgodnych fazach nosi nazwę długości fali , natomiast czas, po którym cząstka rozpoczęła drganie w tej samej fazie jest okresem .

Każda fala charakteryzuje się określoną częstotliwością f , która jest wielkością odwrotną do okresu. Fala w ciągu jednego okresu przebywa drogę , stąd prędkość fazowa rozprzestrzeniania się fali , czyli prędkość rozprzestrzeniania się fazy fali ( prędkość fazowa V ) wynosi:

gdzie: - długość fali

T - okres drgań

f - częstotliwość drgań

Wówczas równanie promienia fali ma postać:

WYZNACZANIE PRĘDKOŚCI ROZCHODZENIA SIĘ FAL AKUSTYCZNYCH O RÓŻNYCH CZĘSTOTLIWOŚCIACH ŹRÓDŁA.

Metoda oparta jest na składaniu drgań harmonicznych o tej samej częstotliwości wzajemnie prostopadłych

Eliminując czas otrzymujemy równanie :

Z powyższego równania widać, że torem cząsteczki jest elipsa.

Układ do pomiarów prędkości głosu metodą składania drgań elektrycznych

1- głośnik

mikrofon

wzmacniacz

Powyższy układ pozwala na wytworzenie dwu drgań elektrycznych, przesuniętych względem siebie w fazie i obserwację wyniku ich złożenia. Do pary płytek X oscyloskopu, w którym wyłączono podstawę czasu, przykładamy napięcie bezpośrednio z generatora. Do pary płytek Y sygnał dociera drogą przez głośnik, mikrofon oraz wzmacniacz i opóźniony w fazie w stosunku do sygnału na płytkach X . Opóźnienie to wynika z różnicy prędkości fali akustycznej i elektromagnetycznej. W zależności od odległości głośnik - mikrofon zmienia się przesunięcie fazowe między obydwoma sygnałami i na ekranie oscyloskopu obserwujemy odpowiadające im krzywe Lissajous.

Przesunięciu mikrofonu z położenia z₁ do położenia z₂ towarzyszy zmiana fazy:

Znając częstotliwość drgań możemy wyznaczyć prędkość fali

gdzie : z₂ - z₁ = k k- liczba całkowita

3) Część praktyczna

Tabela pomiarów

f		z		śr		śr	Vśr	śr
[kHz]	[Hz]	[mm]	[mm]	[mm]	[mm]	[mm]	[m/s]	[m/s]	%
2		195 365 580	170 215	192,5	1	20,5	344	35,74	10,38
2,5		278 410 557	132 147	139,5	1	7,5	348,7	17,51	5,02
3		222 349 453 574	127 104 121	117,3	1	9	352	27	7,67
3,5	100	141 245 343 450 532 633	104 98 107 82 101	98,4	1	8,3	344,4	28,7	8,13
4		132 220 310 397 492	88 90 87 95	90	1	4	360	16	4,44
4,5		154 234 312 384 464 554	80 78 72 80 90	80	1	6,6	360	29,7	8,25
5		139 215 284 354 454 523 607	76 69 70 80 89 84	78	1	8	390	38,87	10,25

Obliczenia

Rachunek błędu

Obliczanie błędu metodą różniczki logarytmicznej

Błąd średni procentowy

4) Wnioski

Ćwiczenie to polegało na wyznaczeniu prędkości dźwięku w powietrzu. Pomiaru tego dokonaliśmy przy pomocy układu zbudowanego z generatora akustycznego i oscyloskopu, na którym obserwowaliśmy złożenie dwóch drgań harmonicznych wzajemnie prostopadłych. Obserwacje przeprowadziliśmy dla różnych częstotliwości z zakresu od 16 Hz do 20 kHz. , przesuwając mikrofon z położenia z₁ do położenia z₂ na linijce . W położeniu z₁ obraz na ekranie oscyloskopu przedstawiał odcinek prostej. Po przejściu mikrofonu do położenia z₂ takiego, że z₂ - z₁ = k /2 obrazem był również odcinek prostej ale o innym nachyleniu ( symetria względem osi Y ) . Przesuwając dalej mikrofon dostaliśmy odraz tak samo usytuowany jak na początku ( z₂ - z₁ = k). Z tych obserwacji mogliśmy więc wyznaczyć długość fali , a znając częstość drgań - prędkość fali. Na błąd pomiarów miały wpływ dochodzące z laboratorium odgłosy, które zakłócały obraz oscyloskopu. Obraz ten zaczynał drgać i ciężko było ustawić mikrofon na skali aby uzyskać idealnie prostą linię. Również błąd generatora akustycznego nie pozostawał bez znaczenia na wynik pomiarów.

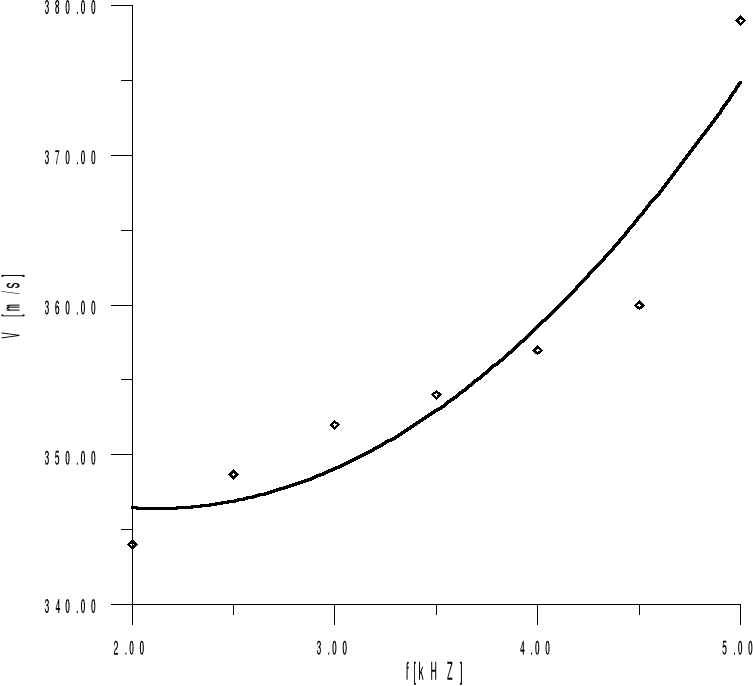
Na podstawie dokonanych obserwacji można wysunąć wniosek, że prędkość rozchodzenia się fali dźwiękowej jest proporcjonalna do częstotliwości. Zależność ta została przedstawiona na wykresie. Z wykresu tego wynika również to, że prędkość fali przy coraz to większych częstotliwościach rośnie znacznie szybciej niż przy częstotliwościach mniejszych.

Uwzględniając błędy i niedokładności otrzymany wynik jest bardzo zbliżony do rzeczywistego, gdyż szybkość rozchodzenia się dźwięku w powietrzu wynosi 340m/s.

---