Politechnika Śląska w Katowicach

Wydział Transportu

Rok akademicki 2007/2008

W wytrzymałości spoin należ zmienić k na k_r

Podstawy Konstrukcji Maszyn

Projekt 1

Temat: Konstrukcja spawana.

Wojciech Pietrzak

Grupa T 37

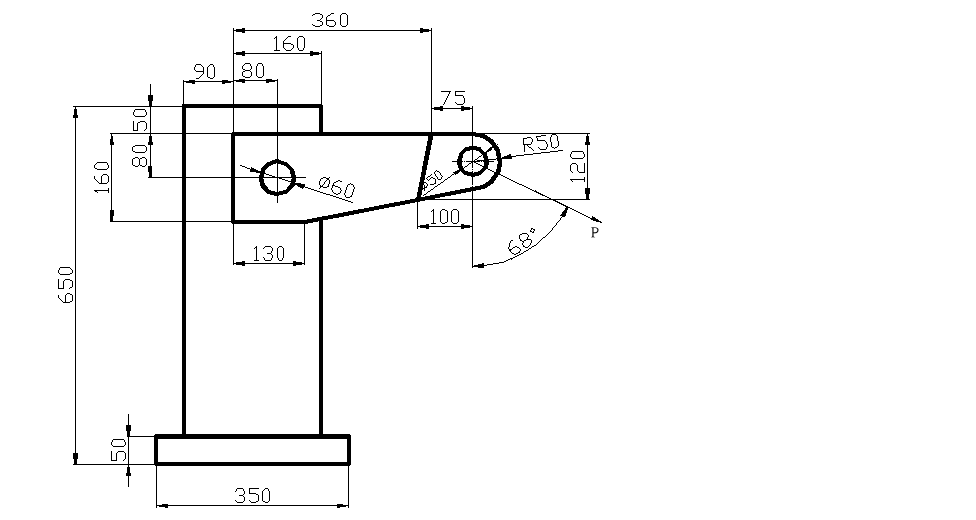
SZKIC I DANE

Konstrukcja jest obciążona siłą statyczną P = 92 [kN] zaczepioną pod kątem α = 68 ˚.

Przyjęty współczynnik bezpieczeństwa konstrukcji x =1,6.Współczynnik jakości wykonania spoiny s₀ =0,8

DANE	OBLICZENIA I SZKICE			WYNIKI
Qr = 315 MPa Qc = 315 MPa Qq = 375 MPa Qs = 195 MPa Qt = 195MPa	Dobrane profile: Podstawa: PN-80/H-92200 Blacha stalowa gruba walcowana na gorąco Wymiary: szerokość 250mm, długość 350mm, grubość 50mm Kolumna: PN-EN 10088 Pręty ciągnione - płaskowniki Wymiary: długość 600mm, szerokość 250mm, grubość 50mm Ramię I PN-EN 10088 Pręty ciągnione - płaskowniki Wymiary: długość 360mm, szerokość 160mm, grubość 40mm Ramię II PN-84/H-93202 Pręty stalowe walcowane płaskie Wymiary: długość 150mm, szerokość 120mm, grubość 40mm Wszystkie części są wykonane ze stali węglowej konstrukcyjnej wyższej jakości C35 dla których dopuszczalne obciążenia odczytano z książki Zbigniewa Osińskiego Podstawy konstrukcji maszyn
x =1,6 Qr = 315 MPa Qc = 315 MPa Qq = 375 MPa Qs = 195 MPa Qt = 195 MPa	Naprężenie dopuszczalne dla elementów konstrukcji			kr = 197 MPa kc = 197 MPa kq = 234 MPa ks= 122 MPa kt = 122 MPa
DANE	OBLICZENIA I SZKICE				WYNIKI
Obliczenie wytrzymałości kolumny w przekroju A-A
sk = 0,25m gk = 0,05m	Pole przekroju; Wskaźnik wytrzymałości przekroju na zginanie;			Ak = 0,0125 m^2
sk = 0,25m t = 0,525 m b1 =0,4m P = 92 kN α = 68˚ b2 = 0,5 m Ak = 0,0125 m^2	Obliczenie występujących w przekroju naprężeń: Ramię działanie składowej pionowej siły P na przekrój b1 = t-0,5sk Zginanie: Ściskanie: Ścinanie:			b1 =0,4m
DANE		OBLICZENIA I SZKICE		WYNIKI
		Obliczenie naprężenie zastępczego: Największym naprężeniem jest zginanie, więc zgodnie z hipotezą wytężeniową Hubera naprężenie zastępcze wynosi:
kg = 234 MPa		Porównanie naprężenia dopuszczalnego z naprężeniem zastępczym: 234 MPa ≥ 111 MPa		Kolumna nie ulegnie zniszczeniu w przekroju A-A
Obliczenie wytrzymałości ramienia I w przekroju B-B
sRI = 0,16m gRI = 0,04m		Pole przekroju: Wskaźnik wytrzymałości przekroju na zginanie		ARI = 0,0056m^2
DANE		OBLICZENIA I SZKICE		WYNIKI
P = 92 kN α = 68˚ b3 = 0,335 m b4 = 0,03 m ARI = 0,0056m^2		Obliczenie występujących w przekroju naprężeń: Zginanie: Rozciąganie: Ścinanie:
		Obliczenie naprężenie zastępczego: Największym naprężeniem jest zginanie, więc zgodnie z hipotezą wytężeniową Hubera naprężenie zastępcze wynosi:
kg = 234 MPa		Porównanie naprężenia dopuszczalnego z naprężeniem zastępczym: 234 MPa ≥ 103 MPa		Ramię I nie ulegnie zniszczeniu w przekroju B-B
Obliczenie wytrzymałości ramienia II w przekroju C-C
DANE		OBLICZENIA I SZKICE	WYNIKI
sRII = 0,1m gRII = 0,04m		Pole przekroju:	ARII = 0,002 m^2
P = 92 kN α = 68˚ ARII = 0,002 m^2		Obliczenie występujących w przekroju naprężeń: Rozciąganie: Ścinanie:
		Obliczenie naprężenie zastępczego Największym naprężeniem jest rozciąganie, więc zgodnie z hipotezą wytężeniową Hubera naprężenie zastępcze wynosi:
kr = 197MPa		Porównanie naprężenia dopuszczalnego z naprężeniem zastępczym: 197 MPa ≥ 52 MPa	Ramię II nie ulegnie zniszczeniu w przekroju C-C
gk = 0,05m		Sprawdzenie wytrzymałości spoiny pachwinowej w połączeniu kolumny z podstawą. Grubość obliczeniowa spoiny:	aI = 0,025m
DANE		OBLICZENIA I SZKICE	WYNIKI
aI = 0,025m lp1 = 0,05m lp2 = 0,25m ep = 0,15m		Obliczenie przekroju spoiny: Wyznaczenie momentu bezwładności spoiny: Środek ciężkości spoiny pokrywa się ze środkiem ciężkości przekroju kolumny. Obliczenie momentu bezwładności względem osi 0Y ( jest to oś działanie momentu gnącego)	ApI = 0,015m^2
ep = 0,15m		Obliczenie wskaźnika wytrzymałościowego przekroju na zginanie:
DANE		OBLICZENIA I SZKICE	WYNIKI
b1 =0,4m P = 92 kN α = 68˚ b2 = 0,5 m ApI = 0,015m^2		Obliczenie naprężeń w spoinie: Dla spoiny pachwinowe wszystkie naprężenia traktuje się jako naprężenia styczne. Zginanie. Wartość siły jak w przekroju A-A dla kolumny: Ściskanie: Ścinanie:
		Obliczenie naprężenia zastępczego:
kt = 122 MPa s = 0,65 s0 = 0,8		Porównanie naprężenia zastępczego z dopuszczalnym: Współczynnik uwzględniający charakter naprężeń s = 0,65 63,4 MPa ≥ 77 MPa	s = 0,65 Spoina pachwinowa łącząca kolumnę z podstawą nie wytrzyma naprężenia

DANE	OBLICZENIA I SZKICE	WYNIKI
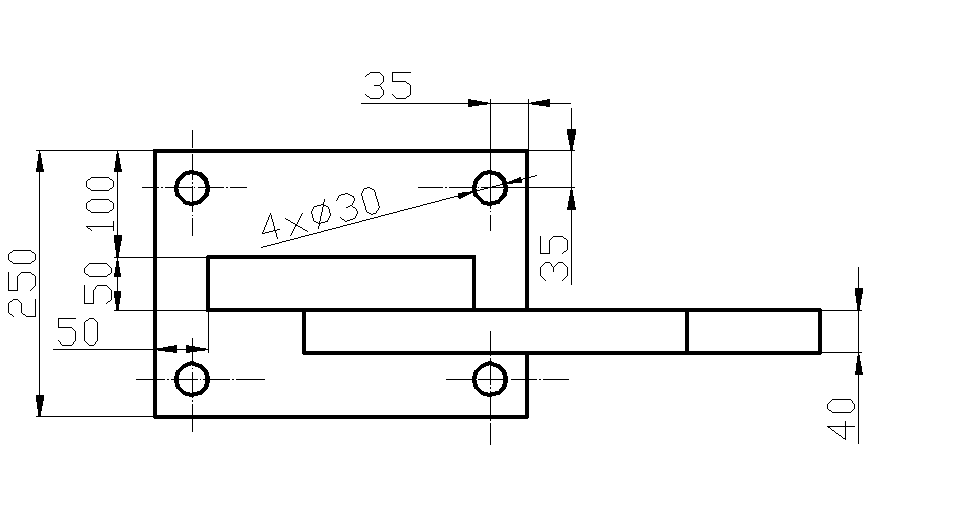
Sprawdzenie wytrzymałości spoiny czołowej 2U w połączeniu ramienia I z ramieniem II.
b5 = 0,12 m b6 =0,025m gRI = 0,04m gRII = 0,04m	Długość spoiny czołowej: Spoina jest wyprowadzana na płytki wybiegowe grubość spoiny czołowej	lc = 0,122m ac = 0,04m
lc = 0,122m ac = 0,04m b5 = 0,12 m	Obliczenie przekroju obliczeniowego spoiny: Wskaźnik wytrzymałości przekroju spoin na zginanie:	Ac = 0,0049m^2

DANE	OBLICZENIA I SZKICE	WYNIKI
b7 = 0,083m b8 = 0,03m P = 92 kN α = 68˚ β = 12˚ Ac = 0,0049m^2	Obliczenie naprężeń w spoinie: Zginanie: Rozciąganie: Ścinanie:
	Obliczenie naprężenia zastępczego: Największym naprężeniem jest zginanie , więc zgodnie z hipotezą wytężeniową Hubera naprężenie zastępcze wynosi:
kg = 234MPa s = 0,65 s0 = 0,8	Porównanie naprężenia zastępczego z dopuszczalnym: Współczynnik uwzględniający charakter naprężeń s = 0,8 150 MPa ≥ 62 MPa	s = 0,8 Spoina czołowa łącząca ramię I z ramieniem II wytrzyma naprężenia

DANE	OBLICZENIA I SZKICE	WYNIKI
gk = 0,05m gRI = 0,04m	Sprawdzenie wytrzymałości spoiny pachwinowej w połączeniu ramienia I z kolumną. Grubość obliczeniowa spoiny:	aII = 0,025m
aII = 0,025m lP3 = 0,16m lP4 = 0,16m lP5 = 0,13m	Obliczenie przekroju spoiny:
aII = 0,025m lP3 = 0,16m lP4 = 0,16m lP5 = 0,13m O1=(0,105;0,1975) O2=(0,0125;0,105) O3=(0,09;0,0125)	Wyznaczenie środka ciężkości spoiny pachwinowej:	XS = 0,078m YS = 0,129m

DANE	OBLICZENIA I SZKICE	WYNIKI
aII = 0,025m lP3 = 0,16m lP4 = 0,16m lP5 = 0,13m O1=(0,105;0,1975) O2=(0,0125;0,105) O3=(0,09;0,0125) XS = 0,078m YS = 0,129m	Obliczenie momentu bezwładności spoiny pachwinowej: Względem środka ciężkości w kierunku osi OX: Względem środka ciężkości w kierunku osi OY Wyznaczenie biegunowego momentu bezwładności
P = 92 kN α = 68˚	Wyznaczenie naprężeń ścinających pochodzących od siły P :
P = 92 kN α = 68˚ e1 = 0,381m e2 = 0,006m	Wyznaczenie momentu skręcającego działającego na spoinę:	MS = 13,6 kNm

DANE	OBLICZENIA I SZKICE		WYNIKI
Wyznaczenie wskaźników wytrzymałościowych na skręcanie i naprężeń skręcających : Współrzędne punktów podane są w metrach S(0,078;0,129) W(0,185;0,21) r1 = 0,134 m U(0;0,025) r2 = 0,13 m T(0;0,155) r3 = 0,15 m
r1 = 0,134 m r2 = 0,13 m r3 = 0,15 m MS = 13,6 kNm		Obliczenie wskaźników wytrzymałościowych na skręcanie: Obliczenie naprężeń skręcających: Do obliczenia naprężenia wypadkowego przyjęto największą wartość naprężenia skręcającego, czyli

DANE	OBLICZENIA I SZKICE		WYNIKI
Wyznaczenie naprężenia wypadkowego: γ = 127˚
kt= 122 MPa s = 0,65 s0 = 0,8		Porównanie naprężenia zastępczego z dopuszczalnym: Współczynnik uwzględniający charakter naprężeń s = 0,65 63,4 MPa ≥ 15,3 MPa		s = 0,65 Spoina pachwinowa łącząca kolumnę z ramieniem I wytrzyma naprężenia
		Wnioski: Z wykonanych obliczeń wynika, że elementy konstrukcji mają wystarczającą wytrzymałość na występujące w tej maszynie naprężenia i nie zostaną zniszczone. Spoina pachwinowa łącząca kolumnę z podstawą nie wytrzyma naprężeń, można temu zapobiec zwiększając grubość ( nawet o 10mm) spoiny oraz poprawiając jakość jej wykonania, reszta spoin wytrzyma naprężenia na nie działające .

14

τ_t

τ_S3

τ_ty

τ_tx

---