Z1

1. Dlaczego układ regulacji musi mieć strukturę zamkniętą?

Wszystkie układy regulacji można podzielić na układy o strukturze :

• otwartej ,

• zamkniętej.

Otwarte układy sterowania spełniają stosunkowo proste funkcje i nie można wymagać od nich dużej dokładności wielkości sterowej y . Często zadaniem takiego układu jest jedynie przestawienie jakiegoś elementu w jedno z dwóch możliwych położeń. W przypadku, gdy położeń tych jest więcej , trzeba zdawać sobie sprawę , że położenie y obarczone będzie błędami spowodowanymi zakłóceniami.

Aby skompensować wpływ zakłóceń działających na układ, trzeba znać wartość oraz kierunek odchylenia wielkości sterowanej od jej wartości zadanej i usunąć to odchylenie przez odpowiednie oddziaływanie urządzenia sterującego na obiekt. Trzeba więc mierzyć rzeczywistą wartość wielkości sterowanej, porównywać ją z wartością zadaną tej wielkości i wynik porównania wykorzystać do skorygowania oddziaływania urządzenia sterującego.

Tak właśnie działają układy o zamkniętej strukturze. Dlatego właśnie układy regulacji muszą mieć strukturę zamkniętą.

O - obiekt

R - regulator

y - wielkość regulowana

w - wartość zadana regulowanej wielkości

e - odchylenie regulacji

x - sygnał nastawiający

z - zakłócenia

z z y

O

x y

R

e w

z

Schemat zamkniętego układu regulacji

2.Określić typ członu i wyznaczyć transmitancję dla układu opisanego równaniem różniczkowym:

Jest to człon inercyjny pierwszego rzędu, gdzie: k- współczynnik wzmocnienia, T - stała czasowa,

Różniczkujemy przekształcenie Laplace'a:

otrzymujemy:

;

3. Podać kryterium stabilności według Lapunowa wraz z interpretacją graficzną.

Definicja stabilności według Lapunowa sformułowana jest dla układów nieliniowych. Dotyczy ona stabilności punktu równowagi układu i opiera się na pojęciu przestrzeni stanów (przestrzeni fazowej). Punkt równowagi nazywa się stabilnym, jeżeli dla każdego dowolnie małego obszaru ε odchyleń od stanu równowagi można dobrać taki obszar η warunków początkowych, że cała trajektoria startująca z obszaru η będzie zawarta wewnątrz obszaru ε.

Definicja Lapunowa dotyczy stabilności układu

w małym otoczeniu punktu równowagi. Taka stabilność nazywa się lokalną, natomiast stabilność punktu równowagi przy dowolnie dużych warunkach początkowych nazywa się globalną.

U₂

ε

η

U_p

U_o U₁

I metoda Lapunowa.

Metoda ta formułuje warunki stabilności lokalnej układu. Załóżmy, że stan równowagi znajduje się w początku układu współrzędnych i układ nieliniowy opisany jest za pomocą równań stanu:

(1)

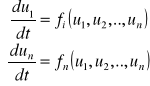
Funkcje f_i(u₁,u₂,...,u_n) można w otoczeniu punktu równowagi rozwinąć w szereg Taylora.

Liniowe przybliżenie powyższego układu równań można przedstawić jako:

(2)

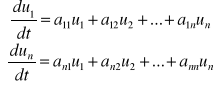
Do badania stabilności tego układu można zastosować znane kryteria stabilności układów liniowych.

Podstawowe tezy I metody Lapunowa:

- jeżeli zastępczy układ liniowy opisany równaniami (2) jest stabilny asymptotycznie, to układ nieliniowy opisany równaniami (1) jest również stabilny asymptotycznie.

- jeżeli zastępczy układ liniowy jest na granicy stabilności, to układ nieliniowy może być zarówno stabilny jak i niestabilny.

II metoda Lapunowa.

Stabilność globalną układu nieliniowego można zbadać za pomocą drugiej metody Lapunowa zwanej bezpośrednią.

I twierdzenie Lapunowa o stabilności:

Układ nieliniowy opisany równaniami stanu (1) jest stabilny asymptotycznie w obszarze D zawierającym początek układu współrzędnych, jeżeli można dobrać taką funkcję V(u₁,u₂,..,u_n) dodatnio określoną w obszarze D, której pochodna względem czasu jest funkcją ujemnie określoną w tym obszarze.

II twierdzenie o niestabilności:

Układ nieliniowy opisany równaniami stanu (1), dla którego istnieje rzeczywista funkcja ciągła V(u₁,u₂,..,u_n) mająca ujemnie określoną pochodną dV/dt = W, jest niestabilny w tym ograniczonym obszarze przestrzeni stanów, w którym V nie jest nieujemnie określona.

Z 2

1. Co wyraża astatyzm układu regulacji?

Astatyzm układu regulacji wyraża to, że układ l-tego rzędu odtwarza bez odchylenia (uchybu) statycznego tylko te wymuszenia, których pochodne począwszy od l-tej są dla dostatecznie dużych czasów równe zero.

Na przykład dla wymuszenia liniowo narastającego ω(t)=at dla uzyskania e_st=0 konieczny jest astatyzmu drugiego rzędu, w przypadku wymuszenia parabolicznego ω(t)=at² - astatyzm trzeciego rzędu. Wymagania te są niemożliwe do spełnienia bez wprowadzenia specjalnych członów korekcyjnych przyspieszających fazę.

w y w y

w(t)

w(t)

e_st→∞

e_st

y(t) y(t)

t t

Przykład odpowiedzi na wymuszenie skokowe i liniowo narastające układów astatycznych I rzędu.

2. Do czego stosuje się transmitancję operatorową a do czego widmową?

Transmitancja operatorowa opisuje własności elementy lub układu liniowego w sposób kompletny jak równanie różniczkowe (jest równoważna równaniu różniczkowemu). Transmitancja operatorowa G(s) elementy lub układu nazywamy stosunek transformaty wielkości wyjściowej y(s) do transformaty wielkości wejściowej x(s) przy zerowych warunkach początkowych. G(s) = y(s)/x(s) Ogólna postać transmitancji operatorowej jest ilorazem dwóch wielomianów zmiennej zespolonej s.

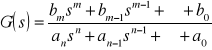
W przypadku elementów o wielu wejściach i wyjściach należy określić macierz transmitancji G(s).

Transmitancja widmowa stanowi teoretyczną podstawę charakterystyk częstotliwościowych, które określają zachowanie elementu lub układu przy wszystkich częstotliwościach wymuszenia, podają stosunek amplitud odpowiedzi do wymuszenia oraz przesunięcie fazowe między odpowiedzią a wymuszeniem jako funkcje częstotliwości. Transmitancję widmową definiuje się:

G(jω) = G(s)/s = jω lub G(jω) = y / x

y - wartość zespolona składowej ustalonej odpowiedzi układu wywołanej wymuszeniem sinusoidalnym;

x - wartość zespolona tego wymuszenia;

Wykresem transmitancji widmowej nazywamy wykres G(jω) (charakterystyka amplitudowo-fazowa, lub zespolona charakterystyka częstotliwościowa).

3. Zadanie.

;

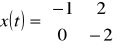
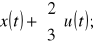
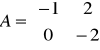
macierz stanu

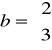
macierz wejść

Warunkiem koniecznym i dostatecznym sterowalności jest aby macierz

była rzędu n. Układ ten aby był sterowalny, wyznacznik z S musi być różny od 0.

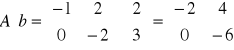
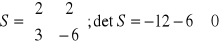
Ponieważ wartość wyznacznika jest różna od 0 więc układ jest sterowalny.

Z 3

1. Co to jest model matematyczny układu dynamicznego. Podać przykład takiego modelu.

Model matematyczny układu dynamicznego sprowadza się do podania związku między wektorem sygnałów wejściowych i wyjściowych - np. w postaci równania różniczkowego, całkowego czy też zależności operatorowej. Występujące w tych równaniach parametry zależą od takich parametrów układu fizycznego jak: masa, współczynnik tarcia, pojemność itp. Mogą one być stałe lub też zależne od czasu oraz od współrzędnych układu. Parametry układu mogą również zależeć od współrzędnych geometrycznych - mówimy wtedy, że jest to układ o parametrach rozłożonych - w przeciwieństwie do układu o parametrach skupionych.

Matematyczny opis układu dynamicznego pozwala na jednoczesne określenie zachowania się układu, pozwala określić sterowalność i obserwowalność układu. Za pomocą aparatu matematycznego można: - dokonać syntezy układu; - przeprowadzić analizę warunków pracy; -ocenić wpływ różnych czynników na obraz modelu.

Opis matematyczny dowolnego elementu składa się z:

- równania (wykresu) charakterystyki statycznej,

- równania różniczkowego lub operatorowego opisującego własności statyczne i dynamiczne w otoczeniu wybranego na charakterystyce punktu pracy.

Przykłady modelu matematycznego układu dynamicznego:

Przykładem zależności od czasu może być zmiana współczynnika wzmocnienia lampy elektronowej na skutek jej starzenia się. Jako przykład zależności od współrzędnych można podać zależność napięcia Zenera od temperatury złącza.

2. Wyznaczyć transmitancję wypadkową układu. Wyznaczyć wartość k (równania charakterystycznego) dla którego transmitancja jest nieokreślona.

Transmitancja wypadkowa:

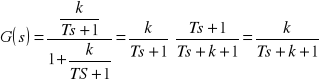
Równanie charakterystyczne: Ts + k + 1 = 0; Ts + k = -1;

k = -1 - Ts;

3. Do czego służy płaszczyzna fazowa? Co to jest trajektoria fazowa?

Istota płaszczyzny fazowej polega na tym, że na podstawie kształtu trajektorii fazowej można określić własności układu dynamicznego: - stabilność, własności dynamiczne, statyczne. Rozwiązaniem układu dynamicznego na płaszczyźnie fazowej o współrzędnych Y i Y' jest trajektoria fazowa, gdzie Y-położenie, Y'-dy/dx-prędkość.

W przestrzeni fazowej możemy badać nie tylko przebiegi w układach swobodnych, lecz także odpowiedzi układu na wymuszenie skokowe, liniowo narastające oraz na dowolne kombinacje tego typu wymuszeń.

Każdemu punktowi w przestrzeni n-wymiarowej będzie odpowiadał pewien stan dynamiczny (faza) układu i odwrotnie, każdy stan dynamiczny układu znajdzie swe odbicie w odpowiednim punkcie tej przestrzeni. Zmianie stanu układu będzie odpowiadał ruch punktu w przestrzeni fazowej, krzywa jaka zakreśli ten punkt w przestrzeni fazowej, nazywa się trajektorią fazową lub krzywą całkową (trajektoria fazowa może niekiedy składać się z wielu krzywych całkowych) - jest to zbiór kolejnych stanów dynamicznych układu. Trajektoria fazowa wychodzi z punktu przedstawiającego warunki początkowe y(0) i :

a) albo kończy się w punkcie równowagi, tzn. w punkcie, w którym wszystkie pochodne funkcji y(t) są równe 0.

b) zdąża do nieskończoności.

c) przechodzi w krzywą zamkniętą, zwaną cyklem granicznym.

Z 4

1.Wyznaczyć charakterystykę l_m członu o transmitancji G(s) = Ts + 1.

G(s) = Ts + 1 = T(jω) + 1 = 1 + jωT;

G(jω) = P(ω) + jQ(ω); G(jω) = 1 + jωT; P(ω) = 1;

Q(ω) = ωT;

Charakterystyka amplitudowa:

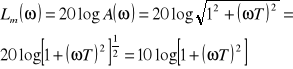
ω	0	10
P(ω)	1	1
Q(ω)	0	10
A(ω)	1	10,5
Lm=20loga(ω)	0	46,13

L_m=20logA(ω) [dB]

46,13

ω

0 1 10

2. Podać określenie dynamicznego układu ciągłego. Co to jest postać normalna układu równań różniczkowych opisujących układ dynamiczny?

Układ dynamiczny to układ, w którym sygnał rozpatruje się jako funkcja czasu. Opisany jest przez trajektorię s={T,W,B}, gdzie T - zbiór chwil czasowych, W - zbiór wartości sygnałów, B - zbiór trajektorii; T > W spełniających prawa rządzące obiektem.

Układ ten jest ciągły, jeśli T = R, gdzie R - zbiór liczb rzeczywistych czyli czas jest zmienną ciągłą.

Warunkiem ciągłości układu jest to, że wszystkie elementy muszą działać w sposób ciągły w czasie i w poziomie tzn., że wszystkie sygnały są funkcjami ciągłymi i mogą przybierać każdą wartość (od najmniejszej do największej) znajdującą się w normalnym obszarze ich zmienności.

Równania różniczkowe mogą posłużyć do opisu matematycznego układu dynamicznego przez podanie związku między wektorem sygnałów wejściowych i wyjściowych. Przy założeniu tradycyjnych oznaczeń stanu układu (x) sygnału wyjściowego (y) model matematyczny naszego układu ma postać normalną:

y = x ;

3. Co to są punkty osobliwe trajektorii płaszczyzny fazowej?

Punkty osobliwe trajektorii są to punkty, w których równanie trajektorii

nie jest jednoznacznie określone (x₂ = 0 ; F(x₁, x₂) = 0). Punkty te są punktami równowagi układu, ponieważ odpowiadają warunkowi x₁=x₂= 0. Można to interpretować jako warunek stanu ustalonego układu. Punktem osobliwym jest prawie zawsze początek układu współrzędnych (x₁=x₂= 0). Liczba tych punktów może być większa od jedności, co więcej można otrzymać zbiory nieskończone (odcinki osi x₁lub całą oś) składające się z punktów osobliwych.

Z5

1.Scharakteryzować wymagania stawiane układom regulacji.

Wymagania stawiane układom regulacji to:

1.Dokładność regulacji - jest to wielkość różnicy miedzy sygnałem wartości zadanej y_o(t), a sygnałem wyjściowym y(t). W praktyce dąży się do uzyskania tzw. dokładności wystarczającej lub określa się dopuszczalną bezwzględną wartość uchybu dynamicznego i uchybu ustalonego. Dokładność dynamiczną osiąga się poprzez dobór parametrów i korekcji regulatora. Dokładność statyczną ustala się na dopuszczalnym poziomie. Kryterium dokładności statycznej jest jednoznaczne: albo układ regulacji jest astatyczny i nie ma uchybu albo jest statyczny i posiada uchyb. Zerowanie uchybu ustalonego osiąga się wprowadzając do regulatora układy całkujące. Dążenie do zerowania uchybu może powodować utratę stabilności.

2.Stabilność regulacji.

Doprowadzenie uchybu ustalonego do wartości zerowej osiąga się poprzez wprowadzenie wymaganego poziomu (stopnia) astatyzmu, czyli liczbę biegunów transmitancji G₀(s).

Ocena stabilności zamkniętego układu regulacji może zostać dokonana na podstawie układu otwartego. Mianowniki wyrażeń określających transmitancje układu zamkniętego zawierają wyrażenie 1+G₀(s), które można traktować jak równanie charakterystyczne: 1+G₀(s) = 0 i znaleźć wartości s, które spełniają to równanie. Aby układ był stabilny, pierwiastki równania charakterystycznego powinny znajdować się w lewej półpłaszczyźnie zmiennej zespolonej s. W praktyce do oceny stabilności stosuje się metody algebraiczne.

3.Wskaźniki regulacji.

- wskaźnik uchybu ustalonego

określa się przez podanie: a) wartości dopuszczalnej w jednostkach fizycznych; b) w jednostkach względnych

- czas regulacji t_r - przedział czasu od chwili wymuszenia do chwili w której uchyb przejściowy ε_p(t)= ε(t)- ε_s , nie przekroczy 5% wartości maksymalnej tj. ε_po.

- współczynnik przeregulowania χ - iloraz największej wartości uchybu ε_p1 o znaku przeciwnym do ε_po i maksymalnej wartości uchybu przejściowego (tj. ε_p0),

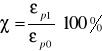
2.Równania układu są następujące:

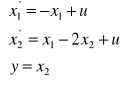
wyznaczyć macierze układu i sterowalność.

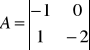
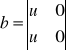
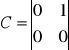
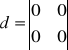
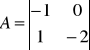
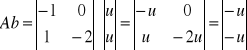
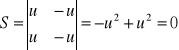
Układ jest niesterowalny.

3.Co to jest transmitancja macierzowa?

Elementami transmitancji macierzowej G(s) są transmitancje łączące poszczególne wejścia i wyjścia.

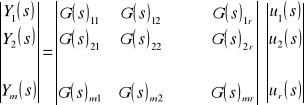
Równania stanu poddajemy przekształceniom Laplace'a:

;

i otrzymujemy

Równanie stanu przyjmuje postać:

Na podstawie równania stanu wyznaczamy:

Wyznaczona wartość transformaty wektora stanu X(s) podstawiamy do równania wyjścia i otrzymujemy:

Dzieląc obustronnie powyższe wyrażenie przez U(s), otrzymujemy wyrażenie na transmitancję macierzową:

W przypadku gdy układ jest układem jednowymiarowym tj. U(t)=u(t), Y(t)=y(t) to transmitancja macierzowa wyraża się:

Z6

1.Co można powiedzieć o własnościach układu dynamicznego na podstawie charakterystyk widmowych (amplitudowo-fazowej, amplitudowej, fazowej)?

Do charakterystyk widmowych zalicza się ch-kę: amplitudowo-fazową, amplitudową i fazową.

Charakterystyka amplitudowo-fazowa G(jω) zwana również zespoloną charakterystyką częstotliwościową lub wykresem transmitancji widmowej określa jak zachowuje się układ bądź element przy różnych częstotliwościach wymuszenia oraz określa kąt przesunięcia fazowego między odpowiedzią a wymuszeniem.

Charakterystyka amplitudowa częstotliwościowa M(ω)=G(jω) jest wykresem modułu ch-ki częstotliwościowej natomiast fazowa ch-ka częstotliwoś. e(ω) = arg G(jω) jest wykresem argumentu ch-ki częstotliwościowej.

ω=∞ ω=0

e(ω_i) Re[G(jω)]

M(ω_i)

ω_k

G(jω)

Ch-ka amplitudowo-fazowa

M(ω)

ω_I ω_k ω

Charakterystyka amplitudowa

e(ω)

ω_I ω_k ω

-90˚

-180˚

-270˚

Charakterystyka fazowa.

2.Wyznaczyć uchyb statyczny układu regulacji

przy wymuszeniu skokowym y_o(t) = 1(t) (przyjąć, że transmitancja

przy wyznaczaniu granicy uwzględnić twierdzenie graniczne rachunku operatorowego).

wymuszenie skokowe y_o(t) = 1(t)

przyjmuję

y_o(t) = 1(t); y_o(s) = 1/s *A

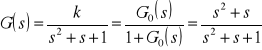
3.Podać przykład charakterystyki statycznej układu nieliniowego i uzasadnić tą nieliniowość.

y

x

Charakterystyka statyczna elementu nieliniowego ze strefą nieczułości.

Układem nieliniowym jest każdy układ zawierający choć jeden element nieliniowy. Układy i elementy nieliniowe opisuje się za pomocą nieliniowych równań różniczkowych lub algebraicznych. Nieliniowość tego układu powoduje, że nie może być wyznaczona wypadkowa odpowiedź na każde z wymuszeń skokowych.

Z 11

1.Podać interpretację: co oznacza jeśli transmitancja G(s) = 0 i jeśli G(s) →∞.

G(s) = 0 - tzn. że transformata sygnałów wyjściowych równa się 0, y(s) = 0;

G(s)→∞ tzn. że x(s)→0 (odpowiedź niepewna)

2.Wyznaczyć logarytmiczną charakterys. amplitudową układu o transmitancji G(s) = sT.

Transmitancja widmowa członu różniczkującego idealnego:

;

a) x(t) b) y(t)=h(t)

f(t)

t t

Charakterystyki czasowe członu różniczkując. idealnego:

a) przebieg sygnału wejściowego

b) odpowiedź skokowa

G(s) = sT; P(ω) = 0; G(jω) = jωT; Q(ω) = jωT;

[dB] Lm

20

+20 dB/dek

10

10^-1 10 10¹

-10

Charakterystyka logarytmiczna amplitudowa członu różniczkującego idealnego.

Nachylenie charakterystyki logarytmicznej amplitudowej wynosi m_o= +20dB/dek. Przechodzi ona przez punkt ω₀=1/k, Im(ω₀) = 0; 20 log kω₀ = 0;

Argument transmitancji widmowej

jest stały, niezależnie od zmian pulsacji.

3.Określić co to jest zapas fazy.

Układ zamknięty jest stabilny, jeśli logarytmiczna charakterystyka amplitudowa układu otwartego posiada wartość ujemną dla pulsacji odpowiadającej przesunięciu fazowemu -π.

[dB] Lm

ω_m ω_a

∆Lm₀ logω[rad/s]

φ(ω
)

ω_m ω_a

log [rad/s]

∆φ₀

-π

Ilustracja graficzna dla przykładu, gdy układ otwarty po zamknięciu pozostaje stabilny. Wynika z niej, że na podstawie przebiegu charakterystyk logarytmicznych modułu i fazy można nie tylko ocenić stabilność układu lecz również podać tzw. „zapas fazy”. Jest to pewien margines bezpieczeństwa, dający pewność, że układ pozostanie stabilny. W języku charakterystyk częstotliwościowych dla układów stabilnych zapas stabilności określa się za pomocą zapasu modułu ∆Im₀ [dB] i zapasu fazy ∆φ₀.

Zapasem fazy ∆φ₀ nazywa się odchylenie charakterystyki fazowej układu otwartego od wartości -180˚ dla pulsacji

ω = ω_m ∆φ₀ = 180˚ + φ₀(ω_m).

Z 12

1.Jak zbadać ciągłość układu dynamicznego?

Układ o działania ciągłym jest to układ, który w skończonym przedziale czasu t przyjmuje nieskończoną liczbę wartości.

x(t)

t

Ciągłość układów dynamicznych określa się na podstawie przebiegów wyjściowych y(t) następujących po wprowadzeniu określonego sygnału wejściowego x(t). Wyznaczenie tych przebiegów (odpowiedzi na wymuszenie) wymaga rozwiązania równania:

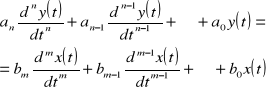
co można wykonać metoda operatorową. Idea tej metody polega na znalezieniu przekształcenia pozwalającego zastąpić równania różniczkowe algebraicznym.

2.Wyznaczyc charakterystykę fazową układu o transmitancji G(s) = sT.

Transmitancja widmowa: G(jω) = Tjω;

część rzeczywista i urojona: P(ω) = 0; Q(ω) = Tω;

φ(ω)

90°

ω

Jest to układ różniczkujący idealny.

3.Określić jaki model układu dynamicznego stosowany jest w metodzie zmiennych stanu.

Modelem stosowany w metodzie zmiennych stanu jest zespół n równań różniczkowych pierwszego rzędu. Obieramy n zmiennych stanu:

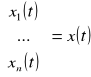
x(t) - wektor stanu;

Załóżmy, że w chwili początkowej t = t₀ znamy wartość zmiennych stanu x₁(t₀), ... ,x_n(t₀). Mówimy, że zbiór liczb {x_i(t₀)} przedstawia stan układu w chwili t = t₀ jeżeli wystarcza on (wraz ze znanym modelem matematycznym i przebiegami sygnałów zewnętrznych) do jednoznacznego określenia zachowania się układu w chwili t > t₀. Wektor stanu kreśli w przestrzeni n-wymiarowej trajektorię stanów. Załóżmy, że układ będzie liniowy, ciągły, stacjonarny. Układ n równań różniczkowych zwykłych wiąże sygnał wejścia z sygnałem wyjścia.

1.Określić transmitancję układu:

R

U₁ C U_c

;

;

gdzie - T = RC;

2.Podać określenie lub definicję dynamicznego układu liniowego i stanu układu.

Układ dynamiczny liniowy można określić następująco:

- równaniem różniczkowym (całkowe, różniczkowe);

- modelem wyjściowo-wyjściowym :

* charakterystyki statyczne

* charakterystyki dynamiczne: (czasowe, częstotliw.)

- transmitancja operatorowa i widmowa, rachunek operatorowy.

Stan układu przy pomocy zmiennych stanu do których należą: - stan układu dynamicznego, - przestrzeń stanu, -wektor stanu, - trajektoria stanu.

Stan układu - najmniej liczny zbiór wielkości, którego znajomość w chwili początkowej t₀ i znajomość wymuszeń w przedziale (t₀, t] pozwala wyznaczyć ilość i odpowiedź układu w dowolnej chwili t > t₀. Najliczniejszy zbiór wielkości, które pozwalają na poznanie zachowania się w przyszłości, czyli jednoznacznie określa zachowanie się układu.

Wg T. Kaczorka - zbiór liniowo niezależnych wielkości, które jednoznacznie określają skutki przyszłych oddziaływań na układ jest wystarczający do wyznaczenia zachowania się układu w przyszłości.

3.Wymień częstotliwościowe wskaźniki regulacji.

Częstotliwościowe wskaźniki regulacji określa się przy pomocy charakterystyk częstotliwościowych (amplitudowych, amplitudowo-fazowych i fazowych):

- częstotliwości granicznej modułu Lm charakterystyki amplitudowej;

- częstotliwości granicznej fazy;

- zapas fazy ∆φ₀;

- zapas modułu (amplitudy ∆Lm) lub wielkości d=│G₀(jω_a)│;←(dla układu otwartego).

Dla układu zamkniętego:

- wskaźnik regulacji:

q(s) - operatorowy wskaźnik;

q(jω) - częstotliwościowy wskaźnik

- częstotliwość rezonansu ω_p.

O

R

Im[G(jω)]

k/TS+1

---