1A

(-4,-2);(1,-2);(1,2);(-4,2) wierzchołki prostokąta

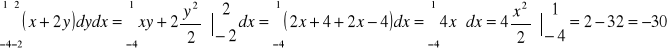
1B

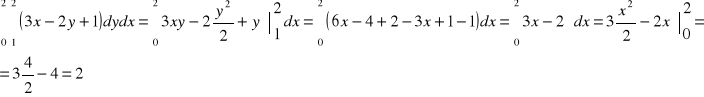
1D

y=x wychodzi z równania prostej przez 2 punkty

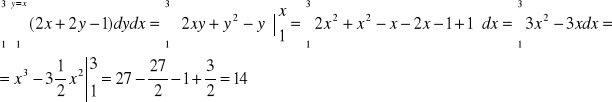
1E

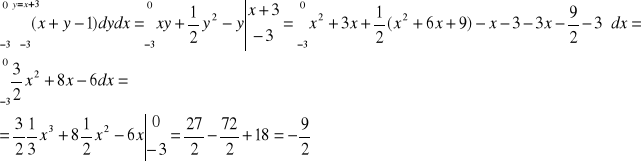
1F

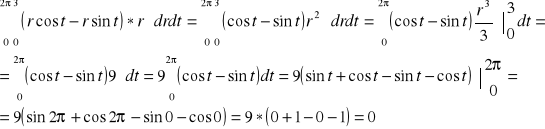
1G

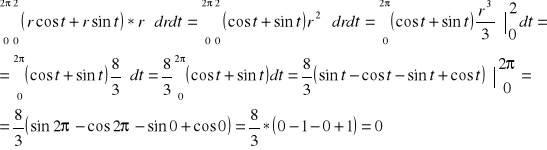
1 H

Z zależności :

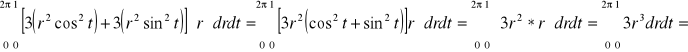
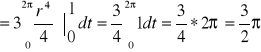
1I

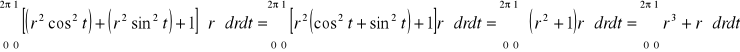
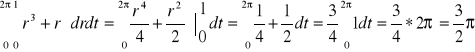
1J

Z zależności :

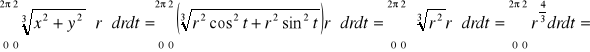
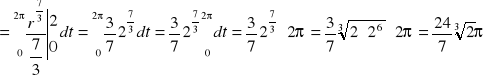
1 K

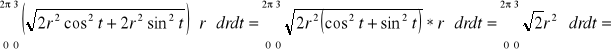
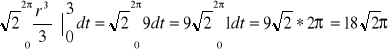
2H

x, y

r₁(t) r₂(t) robimy pochodne z tych wyrażeń po (t)

r'₁(t)=2 (pochodna)

r'₂(t)=1

do wzoru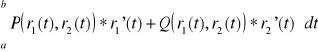
a=0 b=1 bo

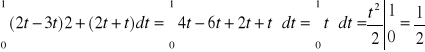
2I

gdzie K jest ćwiartką okręgu o równaniu
skierowana od punktu (1,0) do punktu (0,1)

=>

r'₁(t)=1 (pochodna)

r'₂(t)=

do wzoru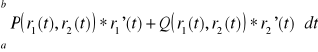
a=1 b=0 bo

(t) jest skierowane od punktu (1,0) do punktu (0,1), jakby punkty były skierowane od (0,1) do (1,0) to a =0 b=1

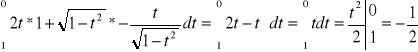
4C

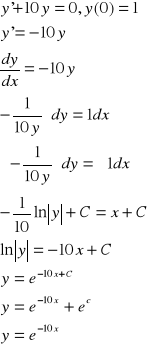
Objaśnienie
oraz

3A

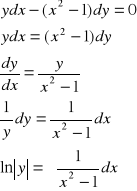
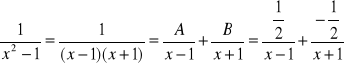
Zamieniamy na inna postać i całkujemy

Ax+A+Bx-B=1

A+B=0 A=

A-B=1 B=

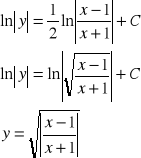
Lub prościej
by obliczyć

3C

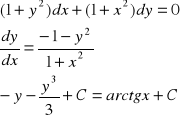
I proszę o wskazówkę

3D

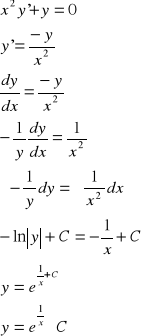
3E

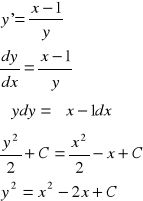
3F

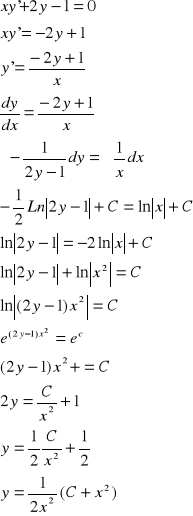
3G

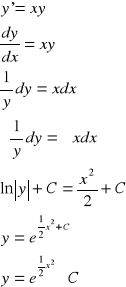
7A

y”+y=0 y(0)=1 ; y'(0)=1

zamieniamy na

r”+r= 0

obliczamy delte
i
oraz miejsca zerowe
<0

r₁= -i

r₂ =i a+bi a =0 b=1

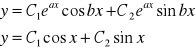
Wiemy ,że y(0)=1

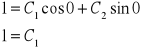
Wiemy też, że pochodna y'(0)= 1 i C1=1

<<= robimy z tego pochodną i wstawiamy za x i y

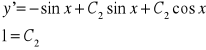
Ostatecznie

7B

y”+8y'+7y=0 y(0)=1 ; y'(0)=1

zamieniamy na

r”+8r'+7r= 0

obliczamy delte
i
oraz miejsca zerowe
>0

r₁= -7

r₂ = -1 wstawiamy do wzoru

Wiemy ,że y(0)=1 równanie powyższe przyjmie postać (w miejsce x wstawiamy 0,a w miejsce y - 1 )

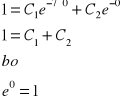
Wiemy też, że pochodna y'(0)=1 x=0 a y'=1

robimy z tego pochodną i wstawiamy za x i y

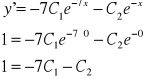
Z układu równań wyznaczamy C1 i C2

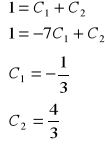
Ostatecznie
w miejsca c1 i c2 wstawiamy wyniki obliczeń

7C

y”-4y'+3y=0 y(0)=2 ; y'(0)=4

zamieniamy na

r”-4r'+3r= 0

obliczamy delte
i
oraz miejsca zerowe
>0

r₁= 1

r₂ = 3

Wiemy ,że y(0)=2

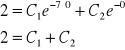
Wiemy też, że pochodna y'(0)=4

robimy z tego pochodną i wstawiamy za x i y

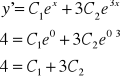
Z układu równań wyznaczamy C1 i C2

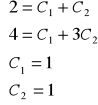
Ostatecznie

7D

y”+4y=0 y(0)=1 ; y'(0)= -1

zamieniamy na

r”+4r= 0

obliczamy delte
i
oraz miejsca zerowe
<0

r₁= -2i

r₂ = 2i a+bi a =0 b=2

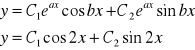
Wiemy ,że y(0)=1

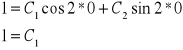
Wiemy też, że pochodna y'(0)= - 1 i C1=1

<<= robimy z tego pochodną i wstawiamy za x i y

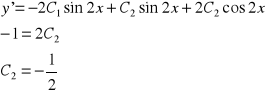
Ostatecznie

7E

y”-2y'+2y=0 y(0)=0 ; y'(0)= -1

zamieniamy na

r”-2r'+2r= 0

obliczamy delte
i
oraz miejsca zerowe
<0

r₁= 1- i

r₂ = 1 + i a + bi wybieramy jedno rozwiązanie i wstawiamy do wzoru poniżej

a= 1 b= 1

wzór gdy delta < 0

Wiemy ,że y(0)=0

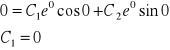
Wiemy też, że pochodna y'(0)= -1

<<= robimy z tego pochodną i wstawiamy za x i y

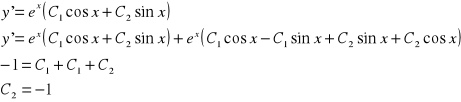
Wstawiamy c1 i c2 do wzoru podkreślonego

Ostatecznie

7F (przykład 6 od p. Cegełki)

y”-y'-3y=3x+1 y(0)=0 ; y'(0)= -2

zamieniamy lewą stronę na

r”-r'+3r= 0 i przyrównujemy do zera

obliczamy delte
i
oraz miejsca zerowe
>0

r₁= -1

r₂ = 1

wiemy ,że y”=0 i y'=A i y=Ax+B wyznaczamy A i B

0 - (Ax+B)=3x+1 -Ax=3x -B=1

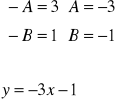
(3) i y(0)=0

(1)

pochodna z tego to :

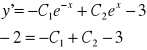
(2) y'(0)=-2

Z (1) i (2) robimy układ równań i obliczamy C1 i C2 i wstawiamy do (3)

C1= 0

C2= 1

Ostatecznie CSRR

7G

y”-y'-12y= -12x-13 y(0)=3 ; y'(0)= 2

zamieniamy lewą stronę na

r”-r'-12r= 0 i przyrównujemy do zera

obliczamy delte
i
oraz miejsca zerowe
>0

r₁= -3

r₂ = 4

wiemy ,że y”=0 i y'=A i y=Ax+B wyznaczamy A i B

0 - A - 12(Ax+B)= -12x-13

-A-12Ax-12B=-12x-13

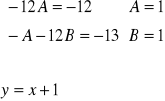
(3) i y(0)=3

(1)

pochodna z tego to :

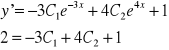
(2) y'(0)=2

Z (1) i (2) robimy układ równań i obliczamy C1 i C2 i wstawiamy do (3)

C1= 1

C2= 1

Ostatecznie CSRR

7H

y”-9y=9x+9 y(0)=2 ; y'(0)= -2

zamieniamy lewą stronę na

r”-9r= 0 i przyrównujemy do zera

obliczamy delte
i
oraz miejsca zerowe
<0

r₁= -3i

r₂ = 3i r =a + bi

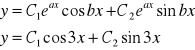
wiemy ,że y”=0 i y'=A i y=Ax+B wyznaczamy A i B

0 + 9(Ax+B)=9x+9 9Ax=9x 9B=9

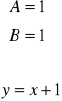
(3) i y(0)=2

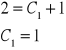
(1)

pochodna z tego to :

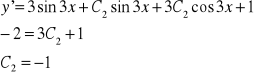
(2) y'(0)=-2

C1 i C2 i wstawiamy do (3)

Ostatecznie CSRR

7 I

y”+3y'-4y= -4x+7 y(0)=2 ; y'(0)= -1

zamieniamy lewą stronę na

r”-r'-12r= 0 i przyrównujemy do zera

obliczamy delte
i
oraz miejsca zerowe
>0

r₁= -4

r₂ = 1

wiemy ,że y”=0 i y'=A i y=Ax+B wyznaczamy A i B

0 +3A - 4(Ax+B)= -4x+7

3A-4Ax-4B=-4x+7

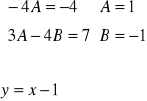
(3) i y(0)= 2

(1)

pochodna z tego to :

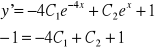
(2) y'(0)= -1

Z (1) i (2) robimy układ równań i obliczamy C1 i C2 i wstawiamy do (3)

C1= 1

C2= 2

Ostatecznie CSRR

7 J

y”+y'-6y= 2x-1 y(0)=
; y'(0)=

zamieniamy lewą stronę na

r”+r'-6r= 0 i przyrównujemy do zera

obliczamy delte
i
oraz miejsca zerowe
>0

r₁= -3

r₂ = 2

wiemy ,że y”=0 i y'=A i y=Ax+B wyznaczamy A i B

0 + A - 6(Ax+B)=2x-1

A-6Ax-6B=2x-1

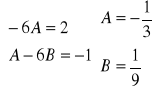
(3) i y(0)=

(1)

pochodna z tego to :

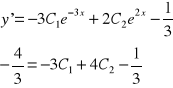
(2) y'(0)=

Z (1) i (2) robimy układ równań i obliczamy C1 i C2 i wstawiamy do (3)

C1= 1

C2= 1

Ostatecznie CSRR

---