eksplikacja

• kolejny rodzaj definicji, który służy do zmniejszenia wieloznaczności

• stosowana do wyrażenia wieloznacznego. Ale ograniczenie wieloznaczności osiągamy inną drogą niż w przypadku definicji regulującej: nie pozostajemy przy niektórych dotychczasowych znaczeniach eksplikowanego wyrażenia, ale respektujemy te znaczenia tylko w pewnej mierze. W pewnej mierze konstruujemy nowe znaczenie

• jak przeprowadzamy eksplikację:

• 1. wypisz wybraną listę zdań, które zawierają wyrażenie W i są tezami przy niektórych znaczeniach wyrażenia W. Te zdania to kryterium adekwatności eksplikacji, jaką chcemy sformułować (jeśli z naszej eksplikacji te zdania będą wynikać, to spełnia ona kryterium adekwatności)

• 2. wybierz język eksplikujący - język zewnętrzny w stosunku do języków, w których dotychczas występowało wyrażenie W

• 3. sformułuj eksplikację, której definiendum (określane tu jako eksplikandum) jest identyczne z wyrażeniem W. A definiensem (eksplikansem) jest pewne wyrażenie W1 języka eksplikującego

• 4. sprawdź, czy eksplikacja jest adekwatna (czyli czy wynikają z niej wybrane uprzednio przez nas zdania stanowiące kryterium tej adekwatności)

• eksplikacja wyrażenia W, które należy do jednorodnych gramatycznie języków J1, J2, J3 - definicja wyrażenia W sformułowana dla języków J1, J2, J3 na gruncie języka J prim (który jest sumą jednego z języków J1, J2, J3 oraz pewnego języka J, zewnętrznego w stosunku do tych języków i zawierającego definiens (eksplikans) tej eksplikacji

• funkcja eksplikacji - ograniczenie wieloznaczności wyrażenia eksplikowanego + po to, by zastosować nowy, zwykle bardziej precyzyjny, aparat pojęciowy, ukształtowany w ramach języka eksplikującego (zewnętrznego) do problemów rozpatrywanych tradycyjnie w języku zawierającym eksplikandum i niejednokrotnie intersubiektywnie nierozstrzygalnych

Język potoczny a język sformalizowany

• język potoczny = etniczny, naturalny

• charakter języka naturalnego sprawia, że niemożliwe jest skonstruowanie wyczerpującego systemu reguł zdających w pełni sprawę ze sposobu używania języka (reguł formowania i reguł dedukcyjnych), o których można byłoby stwierdzić, że ich stosowanie byłoby wystarczające dla zbudowania dowolnego zdania języka naturalnego. Jest tak dlatego, że język naturalny:

• nie powstał w sposób zaplanowany (jak język sztuczny), ale jest rezultatem upowszechnienia się różnego rodzaju niekoordynowanych ze sobą inicjatyw indywidualnych. System jego reguł = niezwykle skomplikowana całość, którą trudno byłoby ogarnąć świadomością

• jest tworem dynamicznym, nieustannie rozwijającym się. Można go przeciwstawić językowi sztucznemu:

• słownictwo naturalnego nie da się scharakteryzować wyczerpująco przez proste wyliczenie, bo bez przerwy pojawiają się nowe słowa i znikają dotychczasowe

• poszczególne słowa i większe całości słowne naturalnego zmieniają swoje kategorie gramatyczne, często, nie tracąc starych, uzyskują nowe i stają się w ten sposób wyrażeniami gramatycznie okazjonalnymi

• tak więc użycie języka naturalnego posiada charakter twórczy

• reguły można sformułować dla języków sztucznych, tak jak robi to logiczna teoria języka, która studiuje reguły językowe charakteryzujące sposób użycia wyrażeń języków sformalizowanych

• języki sformalizowane:

• wszystkie ich reguły wymienione są w sposób wyraźny

• poszczególne kategorie gramatyczne wyrażeń rozpoznawalne są na podstawie formalnych cech tych wyrażeń

• język sformalizowany = płodna poznawczo idealizacja języka naturalnego. Można za jego pomocą badać ogólny sposób funkcjonowania każdego języka naturalnego w procesie komunikacji międzyludzkiej, a także różne sposoby funkcjonowania tego języka w ramach głównych odmian procesów komunikacyjnych [stosunek logicznej teorii języka do badań językoznawczych = taki jak stosunek geometrii do opisowej wiedzy o poszczególnych obiektach fizycznych]

• formalnologiczne badania nad językiem - różny stopień ogólności:

• najmniej ogólne - gdy dotyczą jakiegoś jednego języka sformalizowanego → założenia wyjściowe = reguły wyznaczające jeden określony język

• bardziej ogólne - gdy dotyczą całej obszernej klasy takich języków → założenia wyjściowe charakteryzują ogólnie typ języka reprezentujący cały zbiór różnych, konkretnych języków sformalizowanych, z których każdy ma inne reguły

Klasyczny rachunek logiczny

• stałe logiczne - kwantyfikatory i spójniki takie jak „nie jest tak, że”, „oraz”, „lub”, „jeżeli… to”, „wtedy i tylko wtedy, gdy”

• forma logiczna (schemat logiczny) - schemat zdania, które uzyskamy, pozostawiając bez zmian stałe logiczne oraz pozostałe wyrażenia zastępując zmiennymi

• cecha specyficzna schematów logicznych - to, że zastępując w nich zmienne dowolnymi stałymi, uzyskamy znowu tezy języka

• tautologia logiczna języka J - teza języka J o takiej formie logicznej, że każde zdanie języka J posiadające tę samą formę logiczną jest również tezą języka J. Ustalanie czy coś jest tautologią logiczną odbywa się tak, że ustala się najpierw, jakie schematy logiczne są schematami tautologicznymi (jeśli jakieś zdanie podpada pod schemat tautologiczny, wiadomo, że jest ono tautologią logiczną) → czyli najpierw definiuje się pojęcie schematu tautologicznego a potem określa się tautologię logiczną jako podstawienie pewnego schematu tautologicznego

• schemat tautologiczny - forma (schemat) logiczna zdania będącego tautologią logiczną

• klasyczny rachunek logiczny

• dyscyplina pomocnicza logicznej teorii języka

• odpowiada na pytanie „jakie schematy logiczne są schematami tautologicznymi?”

• 2 etapy:

• rachunek zdań: odpowiedź na pytanie, jakie schematy logiczne zbudowane wyłącznie ze spójników i zmiennych zdaniowych są schematami tautologicznymi

• rachunek kwantyfikatorów: odpowiedź, jakie schematy logiczne zbudowane z wszelkich stałych logicznych i odpowiednich zmiennych są schematami tautologicznymi

• rachunek kwantyfikatorów 1-go rzędu (węższy rachunek funkcyjny) - gdy kwantyfikatory wiążą wyłącznie zmienne indywiduowe

[rachunek zdań i rachunekkwantyfikatorów = dyscypliny formalne (czyli dyscypliny, które określają wyłącznie reguły formowania i reguły dedukcyjne); przyjmuje się tu wyłącznie tezy językowe!]

• w rachunku zdań spójniki zapisuje się w skrótowej postaci:

Spójnik	Zapis	Czyta się
Negacji	~	Nie jest tak, że (nie)
Koniunkcji	Λ	Oraz (i)
Alternatywy	V	lub
Okresu warunkowego (implikacji)	→	Jeżeli, … to
Równoważności	≡	Wtedy i tylko wtedy, gdy

• reguły formowania rachunku zdań:

• reguła ustalająca słownik: znaki kształtu „p”, „q”, „r” oraz znaki kształtu „~” i „→” są słowami rachunku zdań

• reguły ustalające kategorie gramatyczne wyrażeń rachunku zdań: jeżeli dowolne wyrażenie A ma indeks „z”, to wyrażenie „~A” też ma indeks „z”; jeżeli dowolne wyrażenia A, B mają indeks „z”, to wyrażenie „A→B” też ma indeks „z”

• schematy rachunkowo-zdaniowe - wyrażenia rachunku zdań, którym przysługuje indeks „z”

• reguły dedukcyjne (języka) rachunku zdań:

• aksjomatyczna - tezy rachunku zdań:

• (p→q) → [(q→r) → (p→r)]

• (~ p → p) → p

• p → (~ p→q)

• inferencyjne

• podstawiania: jeżeli A jest tezą rachunku zdań, to tezą jest wyrażenie B powstałe z A przez zastąpienie w A dowolnego wyrażenia „p”, „q”, „r” dowolnym schematem rachunkowo-zdaniowym na wszystkich pozycjach, na których wyrażenie to występowało w A

• odrywania: jeśli tezami rachunku zdań są wyrażenia kształtu A oraz A→B, to tezą rachunku zdań jest wyrażenie B

• zastępowania: jeśli tezą rachunku zdań jest wyrażenie C, to jest nią też wyrażenie D powstałe z C w ten sposób, że występujący w C schemat rachunkowo-zdaniowy zastąpiony został schematem rachunkowo-zdaniowym odpowiadającym mu na mocy równości definicyjnych

• zdania wykluczają się = 2 zdania sprzeczne ze sobą nie mogą być jednocześnie prawdziwe

• zdania dopełniają się = 2 zdania sprzeczne ze sobą nigdy nie są fałszywe

• zdania niezgodne = 2 zdania, które się wykluczają

• „prawa De Morgana”

• prawo a: zaprzeczenie komunikacji jest równoważne alternatywie zaprzeczeń

• prawo b: zaprzeczenie alternatywy jest równoważne koniunkcji zaprzeczeń

• p Λ (p → q) → q

• modus ponens - łac. tryb stwierdzający: jeśli prawdziwy jest poprzednik prawdziwego okresu warunkowego, to prawdziwy jest następnik tego okresu: ~ q Λ (p→ q) → ~ p

• modus tollens - łac. tryb obalający: jeśli fałszywy jest następnik prawdziwego okresu warunkowego, to fałszywy jest i poprzednik tego okresu: (p→ q) Λ (q→ r) → (p → r) [sylogizm hipotetyczny]

Stevensa klasyfikacja zmiennych: nominalne, porządkowe, interwałowe, ilorazowe

• zbiór wartości zmiennej przyjmuje postać 1 z 4 skal wyróżnionych przez Stevensa

• typ skali - określa podstawowe operacje empiryczne, jakie można przeprowadzić na zbiorze wartości danej zmiennej, wskazuje dopuszczalne przekształcenia matematyczne, określa jakie statystyki, miary korelacji i testy statystyczne można stosować. Nazwą skali pomiarowej przyjęło się określać typ zmiennej. Tak więc zmienne dzielimy na:

• nominalne (jakościowe) - tylko grupują obiekty (osoby) wg wartości, jakie przyjmują zmienne dla tych obiektów. Np. płeć, bo zmienna ta przyjmuje dla każdej osoby z populacji 1 z 2 wartości. Całą populację można rozdzielić na tyle grup, ile wartości może dana zmienna nominalna przyjmować. Możemy jedynie stwierdzić, czy obiekty są równe czy różne pod względem ich wartości, jakie przyjmuje dla nich zmienna nominalna

• porządkowe - uporządkowanie obiektów wg wartości, jakie przyjmują zmienne dla tych obiektów. Pozwalają na stwierdzenie równości, różności i wykazanie, któremu z obiektów A i B zmienna porządkowa przysługuje w wyższym stopniu

• uporządkowanie silniejsze (całkowite) - gdy zbiór jest uporządkowany przez relację przeciwsymetryczną „<”

• uporządkowanie słabsze (częściowe) - uporządkowany przez relację antysymetryczną („większe lub równe”)

Osoby można uporządkować (porangować) np. wg stopnia przychylności postawy wobec Kościoła, wg wysokości samooceny, wysokości IQ.

Większość zmiennych psychologicznych to, co najwyżej zmienne porządkowe.

• interwałowe (ilościowa) - pozwalają stwierdzić, o ile natężenie zmiennej X dla obiektu A jest większe (mniejsze) od natężenia zmiennej dla obiektu B

• stosunkowe (ilorazowe) (ilościowa) - pozwalają dodatkowo na stwierdzenie, że natężenie zmniennej X dla obiektu A jest „k” razy większe (mniejsze) niż natężenie tej zmiennej dla obiektu B. Np. wiek, czas reakcji

Zmienne - zależne i niezależne. Klasyfikacja zmiennych

• zależna (Y) - jest przedmiotem naszego badania. Jej związki z innymi zmiennymi chcemy wyjaśnić

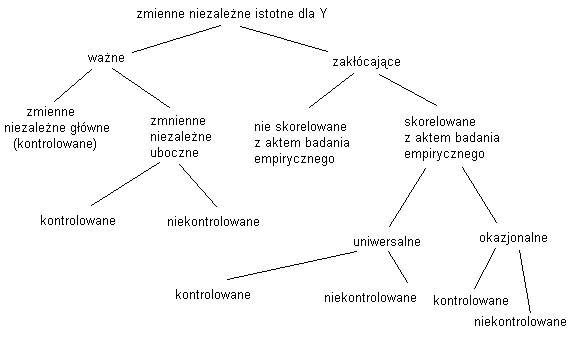
• niezależna (X) - zmienna, od której zależy zmienna zależna. Zmienne niezależne można uporządkować pod względem siły oddziaływania na zmienną zależną (Xg - główne, najsilniej oddziałujące. Xu - uboczne)

• Xg + Xu = W (zmienne ważne dla danej zmiennej zależnej Y)

• Z - zmienne niezależne-zakłócające (mają inferencyjny wpływ na zależność, która wiąże zmienne ważne ze zmienną zależną). Dzielą się na 2 klasy:

• „na zewnątrz” sytuacji badawczej („nie skorelowane” z aktem badania empirycznego). Ich wpływ - „niespecyficzny”, np. indywidualna tolerancja na zmiany ciśnienia atmosferycznego

• „wewnętrzne” względem sytuacji badawczej („skorelowane” z aktem badania empirycznego). To np. zmienne konteksty psychologicznego badania, zmienne będące „pochodną” wchodzenia badacza z osobą badaną w interakcję - oczekiwania badacza, lęk przed oceną, itp.

• N - zmienne niezależne-niekontrolowane = zmienne niezależne-uboczne nie kontrolowane + zmienne niezależne-zakłócające

• K - zmienne niezależne-kontrolowane = zmienne niezależne-główne + reszta zmiennych niezależnych-ubocznych, których wpływ na Y badacz uwzględnia

• zmienne niezależne istotne dla Y = zm. niezależne-główne + zm. niezależne-uboczne + zm. niezależne-zakłócające

Model EX Post Facto (EPF)

Stosowany jest gdy niemożliwe jest zastosowanie modelu eksperymentalnego.

EPF stanowi jakby odwrócenie kolejności czynności badawczych w stosunku do modelu eksperymentalnego. O ile w modelu E chodziło o to, by przez manipulację co najmniej jedną zmienną niezależną - główną wywołać obserwowane zmiany zmiennej zależnej, o tyle w EPF badacz usiłuje zidentyfikować nie znane mu zmienne niezależne, które spowodowały, iż zmienna zależna podjęła określone wartości dla osób z badanej populacji.

Dwie odmiany Modelu EPF

1. odmiana eksploracyjna (EPF-E)

Stosowana w przypadku rozwiązywania problemów istotnościowych, które przyjmują postać następującej kwestii : „ jakie zmienne niezależne są istotne dla zmiennej zależnej”

2. odmiana konfirmacyjna (EPF-K)

Różnica: badacz formułuje hipotezę , która mówi, że zmienna Xj wpływa na zmienną Y. W związku z tym jest on nastawiony na udzielenie rozstrzygającej odpowiedzi : albo Xj jest istotne dla Y albo nie jest.

Wady i zalety modelu EPF

Wady:

Brak możliwości manipulowania zmiennymi niezależnymi istotnymi, gdyż zadziałały już one na zmienną Y w jakieś chwili tj. odległej od tej, w której badacz dokonuje pomiaru zmiennej zależnej Y. Badacz może zaobserwować jedynie efekt tych oddziaływań po upływie określonego czasu.

„grube metody” (wywiad, skale szacunkowe) wprowadzają dość dużą wariancję błędu

Niedogodność natury praktycznej - EPF wymaga celowego doboru grup porównawczych

Zalety:

Względy natury etycznej lub technicznej nie pozwalają badaczowi na zastosowanie modelu eksperymentalnego do rozwiązania danego problemu badawczego.

Ocena istotności zmiennych w modelu EPF

• W tym modelu najczęściej stosowanym testem jest chi- kwadrat. Jeżeli wartość statystki x2 wpada w obszar odrzuceń hipotezy zerowej, uznaje się daną zmienną za istotną dla zmiennej Y. Natomiast jako wskaźnik stopnia, w jakim dana zmienna x1 jest istotna dla Y, używa się współczynnika korelacji punktowo-czteropolowej albo współczynnika Q-Kendalla czy lambda Goldmana i Kruskala.

• Bywa i tak, że o tym czy dana zmienna X1jest istotną dla Y badacze decydują na podstawie przeprowadzonych porównań frekwencyjnych, które mogą wyglądać następująco : zmienna zależna Y, jeżeli jest ona zmienną de facto wielowartościową, podaję się dychotomizacji w jakimś punkcie krytycznym i wyróżnia się 2 grupy osób. Także jako dychotomiczną traktuje się zmienną niezależną i dzieli się całą próbę badana na te osoby, dla których zmienna X1 przyjmuje wartość 1 i dla których przyjmuje wartość 0. Oblicza się procent tych wszystkich 4 kombinacji. Różnica między nimi przekraczająca arbitralnie przez badacza ustaloną wartość progową jest wskaźnikiem istotności zmiennej X1 dla zmiennej Y.

Podstawowe teoriomnogościowe kategorie ontologiczne

• kategorie ontologiczne (kategorie przedmiotów) [ontologia = ogólna nauka o bycie]

• semantyka logiczna wykorzystuje kategorie ontologiczne wyodrębnione w teorii mnogości - bo kategorie ontologiczne teorii mnogości najlepiej odpowiadają kategoriom gramatycznym wyrażeń językowych [teoria mnogości należy do matematyki]

• podstawowe teoriomnogościowe kategorie ontologiczne:

• obiekt indywidualny

• zbiór obiektów indywidualnych

• relacja między obiektami indywidualnymi

• zbiór lub relacja wyższego rzędu

• system relacyjny (struktura)

• „zbiór” - 2 główne znaczenia:

• sens kolektywny (agregat): „zbiór obiektów indywidualnych” = zespół fizycznych elementów tworzących pewną fizyczną całość”

• sens dystrybutywny: „zbiór obiektów indywidualnych” = „ogół tych wszystkich obiektów indywidualnych, które posiadają pewną cechę wspólną (spełniających pewien predykat jednoargumentowy)” [w teorii mnogości zbiór jest pojmowany w tym sensie!]

• związek między cechą a predykatem: przedmiot a posiada cechę f wtedy i tylko wtedy, gdy a spełnia predykat f(x)

• relacje są pewnego rodzaju zbiorami:

• zbiór w szerszym sensie jest relacją (zbiór par uporządkowanych, trójek uporządkowanych, itp.)

• zbiór w węższym sensie jest odpowiednikiem cechy

• suma zbiorów X i Y = zbiór wszystkich i tylko tych przedmiotów, które należą do zbioru X lub zbioru Y (inaczej: do sumy zbiorów X i Y należy każdy taki i tylko taki przedmiot, który należy do X lub Y)

• iloczyn zbiorów X i Y = zbiór tych wszystkich i tylko tych przedmiotów, które należą zarazem do zbioru X oraz do zbioru Y (inaczej: do iloczynu zbiorów X i Y należy każdy i tylko taki przedmiot, który należy zarówno do X, jak i do Y)

• inkluzja (zbiór X zawiera się w zbiorze Y) = gdy każdy element zbioru X jest także elementem zbioru Y

• zbiór X jest identyczny ze zbiorem pełnym = gdy każdy spośród rozważanych przedmiotów należy do zbioru X

• zbiór X jest identyczny ze zbiorem pustym = gdy żaden przedmiot do niego nie należy

• zbiór X jest identyczny z dopełnieniem zbioru X = gdy jest on zbiorem tych wszystkich przedmiotów ze zbioru pełnego, które nie należą do zbioru X

• RELACJA

• relacja R zawiera się w relacji S wtedy i tylko wtedy, gdy każde 2 przedmioty, między którymi zachodzi relacja R, wchodzą także między sobą w relację S (np. relacja kuzynostwa zawiera się w relacji pokrewieństwa)

• relacja R jest zwrotna w zbiorze X wtedy i tylko wtedy, gdy każdy element zbioru X pozostaje w tej relacji do siebie samego (np. relacja bycia rówieśnikiem w zbiorze ludzi). Stosuje się tu kwantyfikator z ograniczeniem (dla każdego x należącego do zbioru X)

• relacja R jest przeciwzwrotna w zbiorze X wtedy i tylko wtedy, gdy żaden element ze zbioru X nie pozostaje w tej relacji do siebie samego (np. relacja starszeństwa w zbiorze ludzi)

• relacja R jest niezwrotna w zbiorze X wtedy i tylko wtedy, gdy nie każdy element zbioru X pozostaje w tej relacji do siebie samego (np. relacja oceny postępowania, bo nie każdy człowiek ocenia swoje własne postępowanie)

• relacja R jest symetryczną w zbiorze X gdy zachodząc między dwoma dowolnymi elementami tego zbioru x i y, zachodzi także między y i x (np. relacja bycia rówieśnikiem)

• relacja R jest przeciwsymetryczną w zbiorze X gdy zachodząc między dowolnymi elementami tego zbioru x i y, nie zachodzi nigdy między y i x (np. relacja starszeństwa)

• relacja R jest niesymetryczną w zbiorze X gdy zachodząc między dowolnymi elementami tego zbioru x i y, nie zawsze zachodzi między y i x (np. relacja oceny postępowania)

• relacja R jest przechodnią w zbiorze X gdy dla dowolnych trzech elementów tego zbioru x, y, z: jeśli zachodzi ona między x i y oraz między y i z, to zachodzi również między x i z (np. relacja starszeństwa)

• relacja R jest spójną w zbiorze X gdy dla każdych dwóch różnych elementów tego zbioru x i y bądź relacja zachodzi między x i y, bądź między y i x (np. relacja większości)

• R jest funkcją określoną na zbiorze X i biorącą wartości z Y gdy każdemu elementowi ze zbioru X odpowiada jeden i tylko jeden element ze zbioru Y

• relacja R jest konwersem relacji R (np. relacja większości jest konwersem relacji mniejszości)

• R jest funkcją jedno-jednoznaczną określoną na zbiorze X i biorącą wartości ze zbioru Y gdy R jest funkcją określoną na X i biorącą wartości z Y, oraz R jest funkcją określoną na Y i biorącą wartości z X

• SYSTEM RELACYJNY (STRUKTURA) = układ elementów, które tworzą pewien zbiór U (uniwersum). Poszczególne elementy należą do zbiorów X1, X2…, zachodzą między nimi relacje R1, R2…

wyjaśnianie faktu szczegółowego = coś innego niż:

• przewidywanie

• postdykcja

• retrodykcja

Ich cechą wspólną jest to, że polegają na sformułowaniu zdania będącego zawsze mniej lub bardziej rozbudowaną koniunkcją zdań prostszych, która zawiera warunki początkowe, z których wynika logicznie pewne zdanie atomiczne lub molekularne.

A różnice są takie:

• we wszystkich 3 przypadkach zdanie będące następstwem logicznym jest hipotezą nie włączoną jeszcze do odnośnego systemu wiedzy empirycznej E

• w przypadku przewidywania odnośne, hipotetyczne następstwo logiczne dotyczy stanu rzeczy, który ma nastąpić później niż chwila, w której dokonano przewidywania

• w przypadku postdykcji odnośne, hipotetyczne następstwo logiczne dotyczy stanu wcześniejszego od czasu dokonania postdykcji

• w przypadku retrodykcji odnośne, hipotetyczne następstwo logiczne dotyczy stanu rzeczy wcześniejszego zarówno od czasu dokonania retrodykcji, jak i od czasu wystąpienia faktu stwierdzonego przez warunki początkowe

Reguły dedukcyjne

• reguły formowania nie wystarczą do uzyskania wiedzy pozwalającej na wykonanie czynności językowej, której sensem jest zakomunikowanie określonego faktu, bo nie każde zdanie oznajmujące komunikuje jakiś fakt (nie komunikują faktu normy. Normy komunikują, podobnie jak zdania rozkazujące, wartości). A nawet jeśli wykluczymy normy, należy stwierdzić, że nie każde zdanie oznajmujące (nienormatywne) komunikuje pewien fakt

• nie komunikują faktów np. kontrtezy danego języka (np. Dziś jest czwartek, jutro będzie sobota). Zaprzeczając kontrtezie otrzyma się zdanie o oczywistej prawdziwości dla każdego, kto zna dany język (Jeśli dziś jest czwartek, to jutro nie będzie soboty) → zaprzeczenie kontrtezy = teza

• ale: poczucie oczywistości nie jest warunkiem ani wystarczającym, ani niezbędnym tego, żeby odnośne zdanie oznajmujące było tezą danego języka (np. zdanie W Polsce znajdują się miasta nie jest tezą)

• zbiór tez każdego języka jest wyznaczony przez reguły dedukcyjne tego języka. Reguły dedukcyjne dzielą się na:

• aksjomatyczne

• nakazują bezwarunkowo uznawać za prawdziwe pewne ustalone zdania, określając je jako tezy

• reguły aksjomatyczne języka J wyodrębniają część tez języka J; charakteryzują postać tych zdań języka J lub po prostu wymieniają kolejno zdania języka J, które są jego tezami

• aksjomaty - zdania języka J wyodrębnione jako tezy przez reguły aksjomatyczne

• inferencyjne

• nakazują uznawać pewne zdania, w sytuacji, gdy uznane już zostały za prawdziwe określone zdania inne

• orzekają, jakie zdania są tezami, jeśli tylko tezami danego języka są pewne inne zdania tego języka

• każda teza języka J jest bądź aksjomatem języka J, bądź bezpośrednią lub pośrednią konsekwencją inferencyjną aksjomatów języka J

• reguł dedukcyjnych można się jedynie domyślać, obserwując sposób użycia zdań danego języka. Chyba że mamy do czynienia z językiem sformalizowanym - wtedy problemów nie ma

• reguły dedukcyjne są szczególnym przypadkiem reguł interpretacji kulturowej

• w języku potocznym, gdy chcemy rozstrzygnąć, czy dane zdanie jest tezą, można posłużyć się kryterium praktycznym - pytaniem: Czy zdanie to jest uznawane za prawdziwe tylko ze względu na samo znaczenie zawartych w nim słów? albo: Czy nieuznanie tego zdania za prawdziwe byłoby świadectwem, że dana osoba nie zna znaczenia zawartych w nim słów? [zdanie języka potocznego uznawane za prawdziwe tylko ze względu na samą znajomość znaczenia zawartych w nim słów, a nie ze względu na jakąkolwiek inną wiedzę, jest tezą języka potocznego]

• wniosek: w skład kompetencji językowej wystarczającej i niezbędnej dla formułowania wyrażeń języka J będących jego zdaniami (oznajmującymi), a przy tym nie będących kontrtezami języka J, wchodzą:

• reguły formowania

• reguły dedukcyjne

• działy logicznej teorii języka:

• składnia logiczna - bada reguły formowania i reguły dedukcyjne

• semantyka logiczna - bada związki między językiem a rzeczywistością

9

---