1. PRZEBIEG ĆWICZENIA:

1. Pomiar wymiarów obciążników w postaci sześcianu, prostopadłościanu o podstawie
prostokąta, prostopadłościanu o podstawie kwadratu. Każdy pomiar wykonujemy
pięciokrotnie.
2. Pomiar czasu 10 wahnięć wahadła nieobciążonego.
3. Pomiar czasu 10 wahnięć wahadła po zamocowaniu w ramce obciążnika w postaci
sześcianu.
4. Pomiar czasu 10 wahnięć wahadła po zamocowaniu w ramce obciążnika w postaci
prostopadłościanu dla trzech głównych osi bezwładności oraz dla głównej przekątnej.
5. Pomiary wymienione w punktach 2 - 4 wykonano trzykrotnie

2.OPRACOWANIE WYNIKÓW

Wymiary obciążników:

Sześcian:

Lp.	1	2	3	4	5
A[mm]	40	40,2	40,1	39,9	40,2
			Średnia:		40,08
(Ai-A)^2[mm]	6,4*10^-3	0,0144	0,0004	0,0324	0,0144
			Odchylenie:		0,06

A=(40,08±0,06)[mm]=(0,04008±0,0006)[m]

Prostopadłościan:

Lp.	1	2	3	4	5
A[mm]	40	40,2	40,1	39,8	40,3
			Średnia:		40,08
(Ai-A)^2[mm]	6,4*10^-3	0,0144	0,0004	0,0784	0,0484
			Odchylenie:		0,09
Lp.	1	2	3	4	5
B[mm]	39,9	40,3	40,1	40	40,2
			Średnia:		40,1
(Bi-B)^2[mm]	0,04	0,04	0	0,01	0,01
			Odchylenie:		0,07
Lp.	1	2	3	4	5
C[mm]	80	80,2	79,8	80,1	80,3
			Średnia:		80,8
(Ci-C)^2[mm]	0,64	0,36	1	0,49	0,25
			Odchylenie:		0,37

A=(40,08±0,09)[mm]=(0,04008±0,00009)[m]

B=(40,1±0,07)[mm]=(0,0401±0,00007)[m]

C=(80,8±0,37)[mm]=(0,0808±0,00037)[m]

Masa sześcianu: = 178,28 g=0,178 [kg]
Masa prostopadłościanu:= 356,86 g=0,357[kg]

Czas 10 wahnięć:

a) Wahadło nieobciążone [t₀]

7,942	7,942	7,941	Średnia	7,942
0	0	1*10^-6	Odchylenie	4,08*10^-4

b) Wahadło obciążona sześcianem[t_s]

8,213	8,213	8,213	Średnia	8,213
0	0	0	Odchylenie	0

c) Wahadło obciążona prostopadłościanem

Względem osi a:[t_PA]

9,220	9,219	9,220	Średnia	9,220
0	1*10^-6	0	Odchylenie	4,08*10^-4

Względem osi b: :[t_PB]

9,220	9,219	9,220	Średnia	9,220
0	1*10^-6	0	Odchylenie	4,08*10^-4

Względem osi c: :[t_PC]

8,476	8,477	8,476	Średnia	8,476
0	1*10^-6	0	Odchylenie	4,08*10^-4

Względem osi głównej przekątnej:[t_pp]

8,719	8,721	8,721	Średnia	8,720
1*10^-6	1*10^-6	1*10^-6	Odchylenie	7,07*10^-4

3)OBLICZENIA

a)Obliczenie okresu drgań

T=1/10*t [s]

1.Okres 1 drgania wahadła nieobciążonego
T₀= (0,7942±0,0004)[s]

2. Okres 1 drgania wahadła obciążonego sześcianem
T_s= (0,8213±0)[s]

3.Okres 1 drgania wahadła obciążonego prostopadłościanem względem osi II a i II b
T_pa=T_pb (0,9220±0,0004)[s]

4. Okres 1 drgania wahadła obciążonego prostopadłościanem względem osi II c
T_pc= (0,8476±0,0004)[s]

5. Okres 1 drgania wahadła obciążonego prostopadłościanem względem głównej przekątnej
T_pp= (0,8720±0,0007)[s]

b) Obliczanie wartości głównych momentów bezwładności dla badanego obciążnika.

Moment bezwładności sześcianu obliczamy ze wzoru:

gdzie:
a = 4,008 [cm] = 0,04008[m]
m_s = 178,28 [g] = 0.178 [kg]

=
∙ 0,178 ∙(0,04008
=4,77*10^-5 [kg∙
]

oraz niepewność

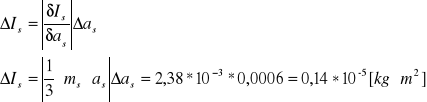
Moment bezwładności dla prostopadłościanu obliczamy ze wzoru

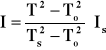
Moment bezwładności względem osi II a=II b

I_I=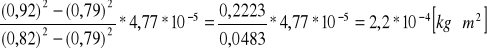

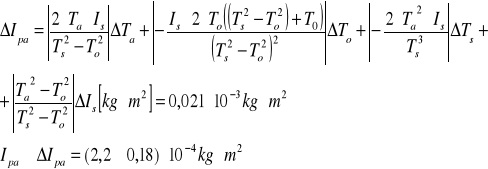
Moment bezwładności względem osi II c

I_II=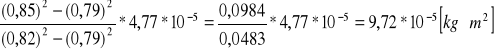

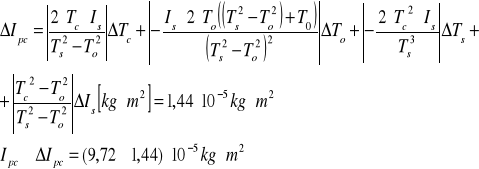
Moment bezwładności względem głównej przekątnej

I_p=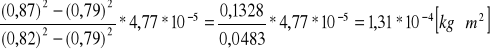

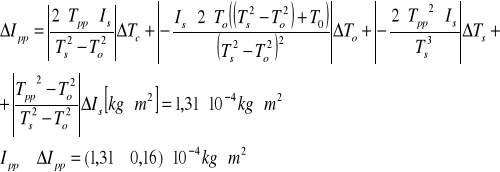
c)Wyznaczanie równania przekątnej prostopadłościanu

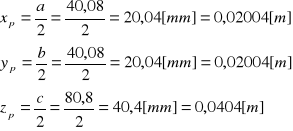
Równanie przekątnej na postać :

d)Wyznaczamy elipsoidę bezwładności prostopadłościanu o podstawie prostokąta :

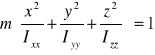
wiemy że I_xx = I_I, I_yy = I_II oraz że I_zz =I_III

więc :

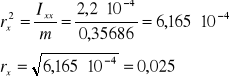
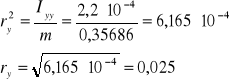
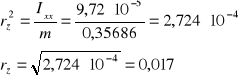
e) Rozwiązywanie układ równań i wyznaczanie punktu przebicia prostej zawierającej przekątną główną z elipsoidą bezwładności:

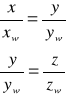
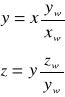
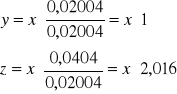
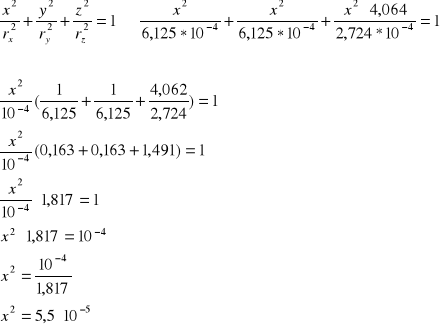
x_p=0,072[m]

y_p=0,072[m]

z_p=0,145[m]

Równanie elipsoidy bezwładności ma postać :

Punkty przebicia prostej elipsoidy bezwładności ma współrzędne:

P=(0,072;0,072;0,145)

Moment bezwładności względem przekątnej głównej prostopadłościanu wynosi :

I_pp2= 0,35686 ((0,072)²+(0,072)² + (0,145)² )

I_pp2= 0,0112[kg·m2]

g) Porównanie wyników

Moment bezwładności ze wzoru pierwszego	Moment bezwładności ze wzoru drugiego
	Ipp2= 0,0112[kg·m2]

Błąd względny wynikający z porównania momentów bezwładności prostopadłościanu względem przekątnej wyznaczonych dwiema metodami

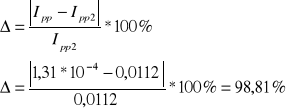
Błąd względny wynosi 98,81%

4)ZESTAWIENIE WYNIKÓW

-pomiary obciążników i czasy wahnięć podane w tabelach

-moment bezwładności względem I głównej osi bezwładności

-moment bezwładności względem II głównej osi bezwładności

­

-moment bezwładności względem głównej przekątnej

-moment bezwładności sześcianu

-równanie elipsoidy

5) WNIOSKI

Celem ćwiczenia było wyznaczyć główne momenty bezwładności sześcianu i prostopadłościanu. Wyniki uzyskane w czasie pomiarów, a także przy obliczeniach są obciążone błędem obserwatora i zaokrąglania liczb. Momenty obliczone dwoma wzorami różnią się, ponieważ korzystano z rożnych wzorów i danych obarczonych różnymi błędami.

6