ESTYMACJA

Szacowanie wartości parametrów w populacji na podstawie próby jest zadaniem estymacji parametrycznej.

Estymacja przedziałowa

Przedziałem ufności nazywamy taki przedział, który z zadanym z góry prawdopodobieństwem (1-α), zwanym poziomem ufności (lub współczynnikiem ufności), pokrywa nieznaną wartość szacowanego parametru Q.

Z reguły przyjmuje się poziom ufności bliski jedności, tzn. (1-α)=0,9; 0,95; 0,99.

-------------------------------------------------------------------------------------------------

-------------------------------------------------------------------------------------------------

Przedziały ufności dla średniej.

Zakładamy, że cecha X ma w populacji rozkład normalny N(m,σ). Niech

m - średnia arytmetyczna w populacji

σ - odchylenie standardowe w populacji

- średnia arytmetyczna z próby

S - odchylenie standardowe z próby

n - liczebność próby

-------------------------------------------------------------------------------------------------

(1) Przedział ufności dla średniej w przypadku, gdy σ - znane, dowolna liczebność próby

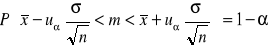
gdzie u_α odczytujemy z tablic rozkładu normalnego dla F(u_α)= 1- ½ α.

-------------------------------------------------------------------------------------------------

(2) Przedział ufności dla średniej w przypadku, gdy σ - nieznane, liczebność próby n < 30

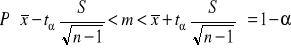
gdzie t_α odczytujemy z tablic rozkładu t-Studenta dla danego α i (n-1) stopni swobody.

-------------------------------------------------------------------------------------------------

(3) Przedział ufności dla średniej w przypadku, gdy σ - nieznane, liczebność próby n ≥ 30, rozkład X w populacji nie musi być normalny

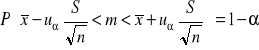
gdzie u_α odczytujemy z tablic rozkładu normalnego dla F(u_α)= 1- ½ α.

-------------------------------------------------------------------------------------------------

-------------------------------------------------------------------------------------------------

Przedział ufności dla wskaźnika struktury.

Niech

p - wskaźnik struktury ( procent wyróżnionych elementów) w populacji,

k - liczba elementów wyróżnionych w próbie

n - liczebność próby

Zakładamy, że n>100, k/n >0,05. Wówczas

-------------------------------------------------------------------------------------------------

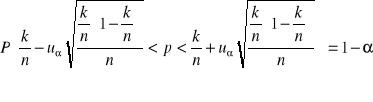
Przy ostrożnym szacunku

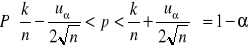
gdzie u_α odczytujemy z tablic rozkładu normalnego dla F(u_α)= 1- ½ α

-----------------------------------------------------------------------------------------------------------------

------------------------------------------------------------------------------------------------

------------------------------------------------------------------------------------------------

Przedział ufności dla wariancji.

Zakładamy, że cecha X ma w populacji rozkład normalny N(m,σ). Niech

σ² - wariancja w populacji

S² - wariancja w próbie

n - liczebność próby

-------------------------------------------------------------------------------------------------

(1) Dla n < 30

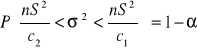
gdzie c₁ - odczytujemy z tablic rozkładu χ² dla (1- α/2) i (n-1) stopni swobody,

c₂ - odczytujemy z tablic rozkładu χ² dla ( α/2) i (n-1) stopni swobody.

(2) Dla n≥30

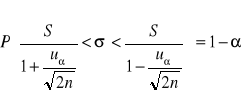
gdzie u_α odczytujemy z tablic rozkładu normalnego dla F(u_α)= 1- ½ α.

-------------------------------------------------------------------------------------------------

Minimalna liczebność próby przy szacowaniu średniej m w populacji (losowanie proste)

Zakładamy, że cecha X ma w populacji rozkład normalny N(m,σ). Niech

m - średnia arytmetyczna w populacji

σ - odchylenie standardowe w populacji

- średnia arytmetyczna z próby

S - odchylenie standardowe z próby

n - niezbędna liczebność próby

n₀ - liczebność próby wstępnej

d - dopuszczalny błąd szacunku

-------------------------------------------------------------------------------------------------

(1) σ - znane, dowolna liczebność próby, cecha X ma w populacji rozkład normalny N(m,σ)

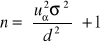
gdzie u_α odczytujemy z tablic rozkładu normalnego dla F(u_α)= 1- ½ α.

[ ] - oznacza całość z liczby

-------------------------------------------------------------------------------------------------

(2) σ - nieznane, liczebność próby n < 30, cecha X ma w populacji rozkład normalny N(m,σ)

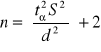
gdzie t_α odczytujemy z tablic rozkładu t-Studenta dla danego α i (n-1) stopni swobody.

-------------------------------------------------------------------------------------------------

(3) σ - nieznane, liczebność próby n ≥ 30, rozkład X w populacji nie musi być normalny

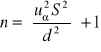
gdzie u_α odczytujemy z tablic rozkładu normalnego dla F(u_α)= 1- ½ α.

Jeżeli n > n₀ to należy dolosować n-n₀ elementów.

Minimalna liczebność próby przy szacowaniu wskaźnika struktury w populacji (losowanie proste)

p - wskaźnik struktury ( procent wyróżnionych elementów) w populacji,

k - liczba elementów wyróżnionych w próbie

n - niezbędna liczebność próby

n₀ - liczebność próby wstępnej

d - dopuszczalny błąd szacunku

-------------------------------------------------------------------------------------------------

Zakładamy, że n>100, k/n >0,05, znamy wskaźnik struktury p w populacji

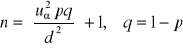
gdzie u_α odczytujemy z tablic rozkładu normalnego dla F(u_α)= 1- ½ α.

Zakładamy, że n>100, k/n >0,05, nie znamy wskaźnika struktury p w populacji

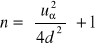
gdzie u_α odczytujemy z tablic rozkładu normalnego dla F(u_α)= 1- ½ α.

PARAMETRYCZNE TESTY ISTOTNOŚCI

-------------------------------------------------------------------------------------------------

Test dla wartości średniej

------------------------------------------------------------------------------------------------

m - średnia arytmetyczna w populacji, m₀- hipotetyczna wartość średniej arytmetycznej w populacji,
- średnia arytmetyczna z próby, σ - odchylenie standardowe w populacji, S - odchylenie standardowe w próbie, n - liczebność próby

-------------------------------------------------------------------------------------------------

(1) Zakładamy, że rozkład cechy w populacji jest normalny N(m,σ) lub zbliżony do normalnego, odchylenie standardowe σ w populacji jest znane.

H₀ : m = m₀

H₁ : m ≠ m₀ (obustronny obszar odrzucenia)

m < m₀ ( lewostronny obszar odrzucenia)

m > m₀ (prawostronny obszar odrzucenia)

Postać statystyki testowej:

Dla obszaru obustronnego u_α odczytujemy z tablic rozkładu normalnego dla F(u_α)= 1- ½ α.

Dla obszaru jednostronnego u_α odczytujemy z tablic rozkładu normalnego dla F(u_α)= 1- α.

Hipotezę zerową odrzucamy gdy:
dla obszaru obustronnego,
dla obszaru lewostronnego,
dla obszaru prawostronnego. W przeciwnym przypadku brak jest podstaw do odrzucenia H₀.

-------------------------------------------------------------------------------------------------

(2) Zakładamy, że rozkład cechy w populacji jest normalny N(m,σ) lub zbliżony do normalnego, odchylenie standardowe σ w populacji jest nieznane oraz n ≤ 30

H₀ : m = m₀

H₁ : m ≠ m₀ , m < m₀ , m > m₀

Postać statystyki testowej:

Dla obszaru obustronnego t_α odczytujemy z tablic rozkładu t-Studenta dla α i (n-1) stopni swobody.

Dla obszaru jednostronnego t_α odczytujemy z tablic rozkładu t-Studenta dla 2α i (n-1) stopni swobody.

Hipotezę zerową odrzucamy gdy:
dla obszaru obustronnego,
dla obszaru lewostronnego,
dla obszaru prawostronnego. W przeciwnym przypadku brak jest podstaw do odrzucenia H₀.

------------------------------------------------------------------------------------------------- (3) Zakładamy, że rozkład cechy w populacji jest normalny N(m,σ) lub dowolny, odchylenie standardowe σ w populacji jest nieznane oraz n > 30.

H₀ : m = m₀

H₁ : m ≠ m₀ , m < m₀ , m > m₀

Postać statystyki testowej:

Dla obszaru obustronnego u_α odczytujemy z tablic rozkładu normalnego dla F(u_α)= 1- ½ α.

Dla obszaru jednostronnego u_α odczytujemy z tablic rozkładu normalnego dla F(u_α)= 1- α.

Hipotezę zerową odrzucamy gdy:
dla obszaru obustronnego,
dla obszaru lewostronnego,
dla obszaru prawostronnego.W przeciwnym przypadku brak jest podstaw do odrzucenia H₀.

-------------------------------------------------------------------------------------------------

Test dla wariancji

------------------------------------------------------------------------------------------------

m - średnia arytmetyczna w populacji,
- średnia arytmetyczna z próby

σ - odchylenie standardowe w populacji, σ₀- hipotetyczna wartość odchylenia standardowego w populacji, S - odchylenie standardowe w próbie, n - liczebność próby

---------------------------------------------------------------------------------------------

Zakładamy, że rozkład cechy w populacji jest normalny N(m,σ), odchylenie standardowe σ w populacji jest nieznane.

H₀ : σ² = σ²₀

H₁ : σ² > σ²₀

Postać statystyki testowej:

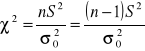
Dla obszaru obustronnego
odczytujemy z tablic rozkładu normalnego dla α i (n-1) stopni swobody. Hipotezę zerową odrzucamy gdy:
. W przeciwnym przypadku brak jest podstaw do odrzucenia H₀. Pamiętając, że

-------------------------------------------------------------------------------------------------

Test dla wskaźnika struktury.

-------------------------------------------------------------------------------------------------

p - wskaźnik struktury ( procent wyróżnionych elementów) w populacji,, p₀- hipotetyczna wartość wskaźnika struktury w populacji, k - liczba elementów wyróżnionych w próbie

n - liczebność próby

Zakładamy, że rozkład cechy w populacji dwupunktowy z parametrem p oraz n>100.

H₀ : p = p₀

H₁ : p ≠ p₀ , p < p₀ , p > p₀

Postać statystyki testowej:

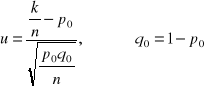
Dla obszaru obustronnego u_α odczytujemy z tablic rozkładu normalnego dla F(u_α)= 1- ½ α.

Dla obszaru jednostronnego u_α odczytujemy z tablic rozkładu normalnego dla F(u_α)= 1- α.

Hipotezę zerową odrzucamy gdy:
dla obszaru obustronnego,
dla obszaru lewostronnego,
dla obszaru prawostronnego. W przeciwnym przypadku brak jest podstaw do odrzucenia H₀.

-------------------------------------------------------------------------------------------------

Test dla dwóch średnich.

-------------------------------------------------------------------------------------------------

m₁ - średnia arytmetyczna w populacji I, m₂- średnia arytmetyczna w populacji II

- średnia arytmetyczna z próby I,
- średnia arytmetyczna z próby II

σ₁ - odchylenie standardowe w populacji I, σ₂ - odchylenie standardowe w populacji II

S₁ - odchylenie standardowe w próbie I, S₂ - odchylenie standardowe w próbie II

n₁ - liczebność próby I, n₂ - liczebność próby II,

-------------------------------------------------------------------------------------------------

(1) Zakładamy, że rozkład cechy w populacjach jest normalny N(m₁,σ₁) i N(m₂,σ₂) lub zbliżony do normalnego, odchylenia standardowe σ₁ i σ₂ w populacjach są znane.

H₀ : m₁ = m₂

H₁ : m₁ ≠ m₂ (obustronny obszar odrzucenia)

m₁ < m₂ ( lewostronny obszar odrzucenia)

m₁ > m₂ (prawostronny obszar odrzucenia)

Postać statystyki testowej:

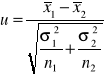
Dla obszaru obustronnego u_α odczytujemy z tablic rozkładu normalnego dla F(u_α)= 1- ½ α.

Dla obszaru jednostronnego u_α odczytujemy z tablic rozkładu normalnego dla F(u_α)= 1- α.

Hipotezę zerową odrzucamy gdy:
dla obszaru obustronnego,
dla obszaru lewostronnego,
dla obszaru prawostronnego. W przeciwnym przypadku brak jest podstaw do odrzucenia H₀.

-----------------------------------------------------------------------------------------------------------------

(2) Zakładamy, że rozkład cechy w populacjach jest normalny N(m₁,σ₁) i N(m₂,σ₂) lub zbliżony do normalnego, n₁≤ 30 i n₂≤ 30, odchylenia standardowe σ₁ i σ₂ w populacjach są nieznane oraz zachodzi równość:
. Normalność weryfikujemy testem Shapiro-Wilka, równość wariancji w populacjach weryfikujemy testem dla dwóch wariancji

H₀ : m₁ = m₂

H₁ : m₁ ≠ m₂ ,m₁ < m₂ ,m₁ > m₂

Postać statystyki testowej:

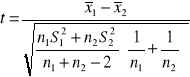
Dla obszaru obustronnego t_α odczytujemy z tablic rozkładu t-Studenta dla α i (n₁+n₂-2) stopni swobody.

Dla obszaru jednostronnego t_α odczytujemy z tablic rozkładu t-Studenta dla 2α i (n₁+n₂-2) stopni swobody.

Hipotezę zerową odrzucamy gdy:
dla obszaru obustronnego,
dla obszaru lewostronnego,
dla obszaru prawostronnego. W przeciwnym przypadku brak jest podstaw do odrzucenia H₀.

-----------------------------------------------------------------------------------------------------------------

(3) Zakładamy, że n₁> 30 i n₂>30 oraz odchylenia standardowe σ₁ i σ₂ w populacjach są nieznane.

H₀ : m₁ = m₂

H₁ : m₁ ≠ m₂ ,m₁ < m₂ ,m₁ > m₂

Postać statystyki testowej:

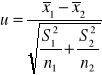
Dla obszaru obustronnego u_α odczytujemy z tablic rozkładu normalnego dla F(u_α)= 1- ½ α.

Dla obszaru jednostronnego u_α odczytujemy z tablic rozkładu normalnego dla F(u_α)= 1- α.

Hipotezę zerową odrzucamy gdy:
dla obszaru obustronnego,
dla obszaru lewostronnego,
dla obszaru prawostronnego.W przeciwnym przypadku brak jest podstaw do odrzucenia H₀.

-------------------------------------------------------------------------------------------------

Test dla dwóch wariancji.

------------------------------------------------------------------------------------------------

Zakładamy, że rozkład cechy w populacjach jest normalny N(m₁,σ₁) i N(m₂,σ₂) lub zbliżony do normalnego, odchylenia standardowe σ₁ i σ₂ w populacjach są nieznane.

H₀ :

H₁ :

Postać statystyki testowej:

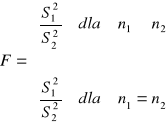
F_α odczytujemy z tablic F-Snedecora dla (n₁ -1) i (n­₂ -1) stopni swobody.

Hipotezę zerową odrzucamy gdy:
. W przeciwnym przypadku brak jest podstaw do odrzucenia H₀.

------------------------------------------------------------------------------------------------

Test dla dwóch wskaźników struktury.

-------------------------------------------------------------------------------------------------

Zakładamy, że populacje mają rozkłady dwupunktowe z parametrami p₁ i p₂ oraz n₁> 100 i n₂>100 .

H₀ : p₁ = p₂

H₁ : p₁ ≠ p₂ ,p₁ < p₂ ,p₁ > p₂

Postać statystyki testowej:

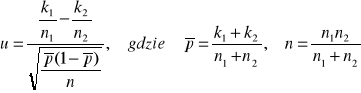
Dla obszaru obustronnego u_α odczytujemy z tablic rozkładu normalnego dla F(u_α)= 1- ½ α.

Dla obszaru jednostronnego u_α odczytujemy z tablic rozkładu normalnego dla F(u_α)= 1- α.

Hipotezę zerową odrzucamy gdy:
dla obszaru obustronnego,
dla obszaru lewostronnego,
dla obszaru prawostronnego.W przeciwnym przypadku brak jest podstaw do odrzucenia H₀.

TESTY NIEPARAMETRYCZNE

Test normalności Shapiro-Wilka

, gdzie
jest dystrybuantą rozkładu normalnego

próba prosta n-elementowa, pobrana z populacji o ciągłej dystrybuancie

poziom istotności

Postać statystyki testowej

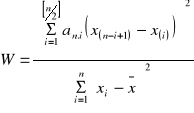
tablicowane współczynniki

uporządkowana próba według wartości rosnących

odczytujemy z tablic wartości krytycznych dla testu Shapiro-Wilka

Obszar odrzucenia
- zatem hipotezę H₀ odrzucamy gdy
-lewostronny obszar odrzucenia.

Test zgodności

, gdzie
jest zbiorem rozkładów o określonym typie postaci funkcyjnej dystrybuanty

n- elementowa próba (n>100, dane przedstawione są w postaci szeregu rozdzielczego o r przedziałach klasowych o liczebnościach
(i=1,…,r)

poziom istotności

Postać statystyki testowej

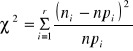
Statystyka ta przy założeniu prawdziwości
ma rozkład
o
stopniach swobody.

k - liczba szacowanych parametrów, które należy wstępnie wyznaczyć na podstawie próby

r - liczba przedziałów klasowych

- prawdopodobieństwo, że zmienna X przyjmuje wartość należącą do i-tego przedziału klasowego, gdy rozkład jest zgodny z

- liczba jednostek, które powinny się znaleźć w i-tym przedziale, przy założeniu, że zmienna ma rozkład zgodny z hipotetycznym

Obszar odrzucenia
(prawostronny), Wartość
odczytujemy z tablic dla (r-k-1) stopni swobody i danego

Test serii losowości próby (test medianowy)

próba jest losowa

próba n-elementowa

poziom istotności

Wyznaczamy Me z próby (w tym celu porządkujemy próbę niemalejąco).

Każdemu wynikowi z próby (według kolejności losowania elementów) przypisujemy symbol:

a gdy
,

b gdy
,

odrzucamy.

Zliczamy:

k - liczba serii

n₁- liczba symboli a

n₂ - liczba symboli b

Obszar odrzucenia dwustronny odczytujemy z tablic rozkładu liczby serii

,

Tablice
;

Test serii dla sprawdzenia hipotezy, że dwie próby pochodzą z jednej populacji

dane:

dwie próby o liczebnościach:

poziom istotności

Wyniki obu prób ustawiamy w jeden niemalejący ciąg. Elementy I próby oznaczamy symbolem a, próby II symbolem b. Zliczamy liczbę serii k

Obszar odrzucenia
odczytujemy z tablic rozkładu liczby serii dla danych
tak, aby
(lewostronny obszar odrzucenia hipotezy zerowej).

Test niezależności chi-kwadrat

W teście niezależności chi-kwadrat hipotezy zerowa i alternatywana mają postać

H₀: cechy X i Y są niezależne (
)

H₁: cechy X i Y są zależne

Z populacji generalnej losuje się co najmniej 100 elementową próbę losową, a jej wyniki grupuje w tablicę o r-wierszach i s-kolumnach, nazywaną tablicą kontyngencji:

X	Y
		n	1
		1

Wnętrze tablicy kontyngencji (korelacyjnej) stanowią liczebności empiryczne
takie, że
. Przez
,
oznaczamy liczebności brzegowe, natomiast
oraz
są prawdopodobieństwami brzegowymi.

Postać statystyki testowej testu niezależności chi-kwadrat

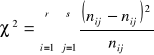
gdzie
są prawdopodobieństwami teoretycznymi.

Statystyka ta ma przy założeniu prawdziwości hipotezy H₀ asymptotyczny rozkład
z (r-1)(s-1) stopniami swobody.

Test ma prawostronny obszar odrzucenia, tzn. że na poziomie istotności α hipotezę H₀ odrzucamy na korzyść hipotezy alternatywnej, gdy
. W przeciwnym przypadku: na poziomie istotności α brak jest podstaw do odrzucenia H₀.

10

---