POLITECHNIKA ŚLĄSKA
WYDZIAŁ ELEKTRYCZNY
Semestr II , grupa T2
Wyznaczanie współczynnika przewodnictwa cieplnego ciał stałych.
Sekcja 2:
Jarosław Janulek
Sebastian Blechinger
1.WPROWADZENIE TEORETYCZNE
Przewodnictwo cieplne jest to proces przepływu ciepła między częściami układu o różnej temperaturze, polegający na przekazywaniu energii ruchu bezładnego jednym grupom cząsteczek przez inne i nie związany z makroskopowymi przemieszczeniami w układzie. Przewodnictwo cieplne prowadzi do wyrównania temp. w układzie
Podstawowym prawem przewodnictwa cieplnego jest proporcjonalność gęstości strumienia ciepła do zmian przestrzennych temperatury T, zwane prawem Fouriera:
![]()
jg=-gradT lub
gdzie:
jg- gęstość strumienia energii,
- współczynnik przewodnictwa cieplnego,
- strumień energii przepływający przez powierzchnię S.
Według tego prawa przewodnictwo cieplne to przenoszenie energii, która powstaje przy różnicy temperatur jakie powstają w ciele stałym tzn, że strumień energii przepływający przez powierzchnię S ustawioną prostopadle do kierunku, w którym przepływa energia cieplna w czasie T jest proporcjonalny do przyrostów ( gradientu ) temperatury.
![]()
Jeśli zastąpimy pochodną cząstkową przyrostami temperatur:
oraz podstawimy zależność napięcia od temperatury:
T=U*g
gdzie: g to współczynnik proporcjonalności,
![]()
to po przekształceniach otrzymamy wzór zależności strumienia energii od przyrostu napięcia U:
![]()
Następnie korzystając z tego, że płyty są ściśle połączone ze sobą przez co nie zachodzi zjawisko rozpraszania strumienia energii możemy porównać strumienie energii dla poszczególnych materiałów. Po przekształceniach otrzymamy wzory zależności współczynników przenikalności drewna 2 i piaskowca 3 od współczynnika przewodnictwa cieplnego marmuru , który znamy.
gdzie: dx-grubość materiału mierzonego,
d1-grubość materiału wzorcowego,
Ux- przyrost napięć materiału mierzonego,
U1-przyrost napięć materiału wzorcowego,
Schemat układu i opis termopary.
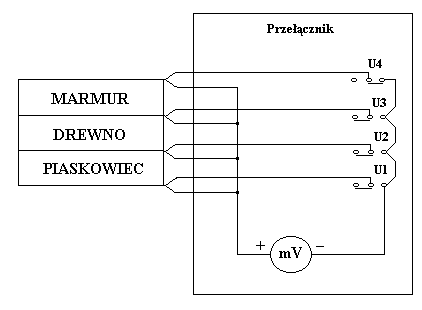
Termopara jest to obwód złożony z połączonych ze sobą różnych kawałków metali.
Podczas przepływu strumienia ciepła spowodowanego różnicą temperatur wytwarza się tzw. siła termoelektryczna. Termopara służy do elektrycznego pomiaru temperatur poprzez mierzenie siły termoelektrycznej, która jest proporcjonalna do temperatury.
Et=a(T2-T1)
gdzie:
a-stała termopary zależna od rodzaju metali tworzących termoparę.
Przy pomocy układu pokazanego na rysunku możemy mierzyć siłę termoelektryczną powstającą w termoogniwach, przez które przepływa strumień energii i które są połączone ze sobą.
Siła termoelektryczna powstaje w układzie dwóch półprzewodników lub przewodników różnych od siebie, których końce znajdują się w innych temperaturach.
2.PRZEBIEG ĆWICZENIA
Aby wyznaczyć współczynnik przy pomocy układu pokazanego na schemacie należy podgrzać wodę w kolbie do temp. wrzenia, aby podgrzewanie materiałów było jednostajne. Następnie należy zacząć mierzyć zmiany temperatury materiałów w czasie. Pomiary te należy dokonywać w odstępach minutowych aż do ustalenia się temperatur na wszystkich materiałach tzn. ustalenia się równowagi termodynamicznej układu.
3.OPRACOWANIE WYNIKÓW
1.Uzupełniamy wodę w naczyniu.
2.Otwieramy obieg zimnej wody i rozpoczynamy podgrzewanie wody w naczyniu.
3.Od momentu zagotowania wody zaczynamy notować wskazania miliwoltomierza mierzącego siłę termoelektryczną kolejnych termopar.
4.Pomiary powtarzamy w odstępach minutowych aż do ustalenia się wskazań miernika dla poszczególnych termoelementów.
5.Rysujemy wykresy zależności siły termoelektrycznej od czasu i określamy ustalone wartości tej wielkości dla kolejnych termopar.
6.Obliczamy współczynnki przewodnictwa cieplnego dla drewna i piaskowca.
7.Przeprowadzamy rachunek błędów.
Grubość:
-marmuru: d1=23.8mm
-drewna: d2=16.9mm
-piaskowca: d3=16.7mm
Współczynnik przewodnictwa cieplnego marmuru: 1=2.33 [J/msK]
4.TABELE POMIAROWE
Do obliczeń przyjęto błąd wynikający z niedokładności odczytu z miliwoltomierza:0.03[mV]
Wartości i 3 obliczyliśmy ze wzoru:
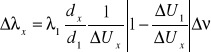
![]()
a następnie błąd obliczeń z definicji różniczki zupełnej: i
Otrzymaliśmy następujące wyniki:
materiał |
różnica potencjałów |
λ [J/msK] |
Δλ[J/msK] |
drewno |
0.08 |
2.04 |
0.16 |
piaskowiec |
1.22 |
0.13 |
0.04 |
marmur |
0.1 |
2.33 |
--------- |
Obliczenia:
![]()
-dla piaskowca:
![]()
Błąd obliczenia 3:
![]()
-dla drewna:
![]()
Błąd obliczenia 2:
5.WYKRESY
6.WNIOSKI I UWAGI
Po dokonaniu obliczeń otrzymaliśmy następujące wartości współczynników:
![]()
![]()
![]()
Porównując je z danymi odczytanymi z tablic, według których:
![]()
![]()
stwierdzamy, że pomiary wykonane dla piaskowca są prawidłowe, natomiast dla drewna są obarczone niewielkim błędem.
![]()
![]()
![]()
![]()
![]()
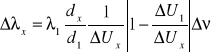
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
8 BLECHINGER, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, La
Lepkość-sciaga, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
Nr ćwiczenia5 moje, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
[4]tabelka, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, labo
[8]konspekt new, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
FIZYK~47, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Fizyka
3 W LEPKO CIECZY, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
[3]opracowanie v1.0, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labo
kospekt12, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, 12 Wyznaczanie
PUZON, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Laborki s
cw8 wyniki, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, labo
[4]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
mostek Wheatstone'a(1), Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, l
za, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, laborki fizy
konspekt nr8, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Fi
[7]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
więcej podobnych podstron