P O L I T E C H N I K A W R O C Ł A W S K A WYDZIAŁ ELEKTRONIKI INFORMATYKA (I rok)
Laboratorium Miernictwa Elektronicznego - Grupa I (środa TP, godz. 17^05)
Imię i Nazwisko:		Paweł Płaza Krzysztof Różczka	Data Wykonania: 1997.04.02 Ocena:
Nr ćwiczenia: 3 Temat: Pomiar parametrów sygnałów sinusoidalnych metodą próbkowania i cyfrowego przetwarzania

1. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie z metodą próbkowania i kwantowania sygnału napięciowego, poznanie środków technicznych stosowanych w tej metodzie oraz źródeł i charakteru błędów, występujących w pomiarach parametrów sygnałów.

2. Dane techniczne przyrządów

• Woltomierz cyfrowy V 541: uchyb podstawowy:

• dla 40Hz*10kHz : *0.05% wartości mierzonej, *0.05% pełnej skali,

• dla: 20Hz*40Hz i 10kHz*20kHz

• *0.1% wartości mierzonej,

• *0.05% pełnej skali,

• impedancja wejściowa na zakresie 1V i 100mV - 10MW//80pF,

• impedancja wejściowa na pozostałych zakresach - 1MW//80pF,

• Częstościomierz C 549 A: dokładność: *1 na ostatnim miejscu

*1 dokładności użytego generatora podst. czasu,

czas odczytu: 2s *20%,

zakres: do 20 Mhz,

wzorzec wewnętrzny: 1MHz, dokładność częstotliwości (przy +20°C *5°C): *10^-5

• Karta przetwornika a/c: zakres -5..+5V

3. Badanie sygnału mierzonego dla okna czasowego mieszczącego 2.5 okresu sygnału

Pomiary przeprowadzone zostały dla częstotliwości 50 Hz i napięcia U=1.699V (zmierzonego woltomierzem cyfrowym V541). Dla częstotliwości sieciowej 50Hz woltomierz ten posiada możliwość wyeliminowania składowej stałej napięcia. Po regulacji składowa stała napięcia wynosiła U_= 0.009 V.

Spis wartości wielkości odczytanych z przyrządów podczas pomiarów:

U = 1.699 V

DU = 0.05⋅1.699 + 0.05⋅zakres=

U_=0.009 V = 9 mV

f_G = 50 Hz

t_G = 20.036 ms

N = 100 (ilość próbek)

Aby dobrać okno czasowe pomiaru T_WP, które obejmuje 2.5 okresu sygnału badanego, należy dobrać odpowiednią częstotliwość próbkowania f_S:

Podczas pomiarów komputer automatycznie wykonuje obliczenia estymatorów wartości średniej i skutecznej badanego sygnału według wzorów:

wartość średnia: wartość skuteczna:

Dla 2.5 okresu w oknie pomiarowym dla zakresu U= 4.827 V, zakresu t= 50 ms, ilości próbek N=100 i częstotliwości próbkowania f_S= 2 kHz obliczone wartości średnie i skuteczne wynoszą:

m = 2.368 mV i s = 1.697 V.

Poniżej zestawiona jest tabela zawierające wyliczone dane dla różnych zawartości okresu w oknie pomiarowym:

Ilość okresów w oknie	0.25	0.5	0.75	1	1.25	1.5	1.75	2	2.25	2.5
m [mV]	1.358V	-118.900	-494.100	54.900	293.700	-38.860	-215.500	26.920	165.300	2.368
s [V]	1.609	1.730	1.668	1.719	1.682	1.710	1.687	1.709	1.690	1.697
tK [ms]	5	10	15	20	25	30	35	40	45	49.5
UK [V]	-190.4m	-2.415	178.2m	2.390	-170.9m	-2.432	163.6m	2.390	-153.8m	-2.400
st [ms]	5	10	15	20	25	30	35	40	45	49.5
sU [V]	2.576	4.800	4.800	4.810	4.810	4.827	4.827	4.827	4.827	4.827
DUŚR [mV]	-7.642	-127.900	-503.100	45.900	284.700	-47.860	-224.500	17.920	156.300	-6.632
dUŚR [%]	-562.739	107.569	101.821	83.607	96.936	123.160	104.176	66.568	94.555	-280.068
DUSK [V]	-0.092	0.029	-0.033	0.018	-0.019	0.009	-0.014	0.008	-0.011	-0.004
dUSK [%]	-5.718	1.676	-1.978	1.047	-1.130	0.526	-0.830	0.468	-0.651	-0.236

Obliczenia błędów:

Wykresy błędu pomiaru wartości średniej i skutecznej w funkcji ilości okresów mieszczących się w oknie czasowym:

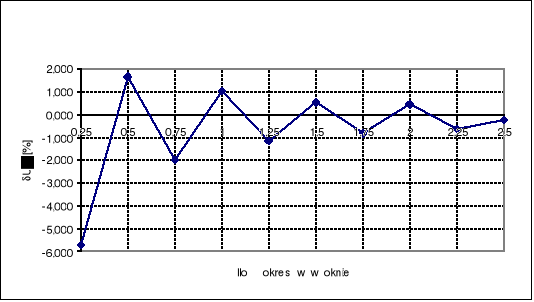
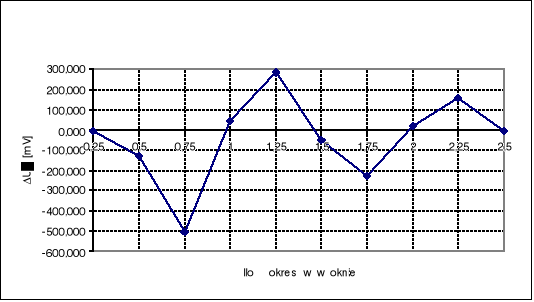
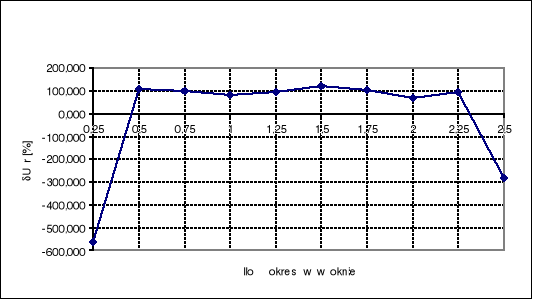
Z przeprowadzonych pomiarów wynika, że podczas pomiaru wartości napięcia skutecznego, błąd pomiaru aperiodycznie maleje do zera wraz ze wzrostem liczby okresów przebiegu zawartych w oknie czasowym. Dla 2.5 okresów w oknie był on już w przybliżeniu równy zeru.

Przeprowadzanie pomiarów wartości średniej napięcia dla małej liczby okresów w oknie nie ma sensu, ponieważ błędy pomiarów są bardzo duże i wynoszą nawet kilkaset procent (dla niepełnego okresu w oknie). Dla pełnej liczby okresów w oknie błędy napięcia średniego stopniowo zmniejszają się (co widać na wykresach). Dla małej liczby okresów w oknie czasowym (np. dla 1) zmierzona wartość jest przeszło 500% większa od wartości zmierzonej przyrządem V541. Dla 2 okresów w oknie różnica ta wynosi już około 300%. Podczas pomiaru wartości średniej napięcia trudno jest utrafić z próbką na początek badanego sygnału (1) (rysunek), gdyż układ próbkujący nie ma impulsu startowego (1) i próbkowanie rozpoczyna się od miejsca (2) - aby zmniejszyć błąd należałoby „zgubić” jedną próbkę. Już podczas pomiaru dwóch okresów badanego przebiegu mieszczących się w oknie czasowym wpływ tego zjawiska jest zauważalnie mniejszy (błąd względny napięcia średniego zmniejszył się z 83.6% do 66.6 %). Widać stąd, że pomiar wartości średniej napięcia dla małej liczby okresów w oknie czasowym mija się z celem. Na błąd pomiaru wartości średniej ma także wpływ błąd kwantowania i niedokładność napięcia poprawnego (mierzonego woltomierzem cyfrowym, który także posiada pewien błąd). Jednak czynniki te tylko w niewielkim stopniu wpływają na ogólną wielkość błędu napięcia średniego przebiegu.

4. Badanie sygnału (1 okres w oknie) dla stopniowo zmniejszanego okna czasowego

Pomiary wykonane dla: N = 100, f_S = 4950 Hz, zakres t = 20.2020 ms, U_V541 = 1.698 V tak, że w oknie pomiarowym mieścił się jeden okres.

zmniejszenie okna o:	0 %	1 %	2 %	5 %	10 %
m [mV]	-7.349	-1.184	3.637	8.441	-21.89
s [V]	1.692	1.700	1.708	1.743	1.786

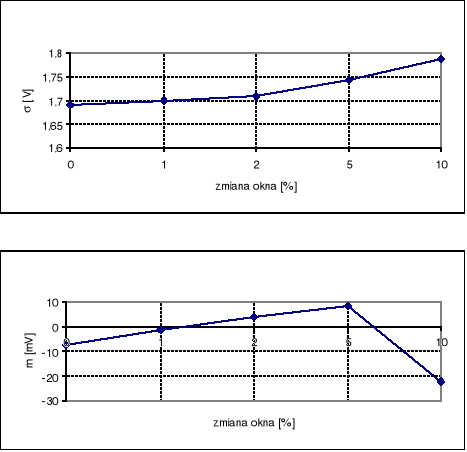
Z przeprowadzonych pomiarów wynika, że wraz ze zmniejszaniem okna pomiarowego wartość estymatora wartości skutecznej liniowo wzrasta (przy zmniejszeniu okna o 10% o 0.094 V), natomiast dla estymatora wartości średniej przy zmniejszeniu okna o 5% wartość liniowo wzrasta, a przy dalszym zmniejszeniu okna o 5% gwałtownie maleje.

5. Błąd kwantowania i przykładowe obliczenia

Operacje próbkowania i kwantowania realizowane są za pomocą próbkujących przetworników a/c. Rzeczywiste sygnały x(t) mają początek i koniec i są próbkowane w określonym czasie T_W (oknie czasowym). Stąd w praktyce dysponujemy pewnym skończonym zbiorem skwantowanych próbek. Zbiór próbek x(k) wystarcza do analizy sygnałów okresowych i jednorazowych. Wyniki analizy są obarczone błędami, spowodowanymi przede wszystkim ograniczonym czasem próbkowania oraz kwantowaniem sygnału. Błąd kwantowania e(t) wyznacza się z zależności:

e(t) = x(k) - X(k)

gdzie x(k) jest wynikiem kwantowania, a X(k) - wartością rzeczywistą próbki.

Maksymalny błąd kwantowania wynosi:

oznaczenia we wzorach: q- ziarno przetwornika, Q - liczba bitów przetwornika.

Do opisu błędu kwantowania przyjmuje się zazwyczaj model statystyczny. Zakłada się wtedy, że wartości e(k) są próbkami szumu białego o rozkładzie równomiernym gęstości prawdopodobieństwa w przedziale amplitud p_S(x) definiowanym jako:

Wartość odchylenia średniokwadratowego d wynosi:

W nieidealnym przetworniku mogą występować błędy nieliniowości charakterystyki przetwarzania. Nieidealność przetwornika uwzględnia się często przez mnożnik r

W przypadku posługiwania się modelem statystycznym w pomiarach wartości średniej i skutecznej można obliczyć wartości graniczne błędu przypadkowego na poziomie ufności p, zakładając normalny rozkład gęstości prawdopodobieństwa błędu mierzonej wartości. Korzysta się wtedy ze standardowych reguł:

D (N,p) = t_N,p d

gdzie t_N,p jest wartością standaryzowanego rozkładu Studenta na poziomie ufności p.

Graniczny błąd przypadkowy dla poziomu ufności p dla każdej próbki ze zbioru próbek

Graniczny błąd przypadkowy wartości średniej z N pomiarów:

Graniczny błąd przypadkowy wartości skutecznej (dla małych błędów w porównaniu z wartością skuteczną):

Błąd systematyczny wartości skutecznej, powodowany dodawaniem się mocy szumu kwantowania do mocy sygnału:

Przykładowe obliczenia:

Ziarno przetwornika wynosi:

Błąd graniczny pojedynczej próbki:

Wartość współczynnika r zależy od jakości wykonania przetwornika. Dla rzeczywistego przetwornika można przyjąć r=2. Zatem:

Odchylenie średniokwadratowe zbioru próbek dąży do wartości:

Graniczny błąd przypadkowy dla przyjętego poziomu ufności p dla każdej próbki ze zbioru próbek

Graniczny błąd przypadkowy wartości średniej z N pomiarów:

Graniczny błąd przypadkowy wartości skutecznej (dla małych błędów w porównaniu z wartością skuteczną):

Błąd systematyczny wartości skutecznej, powodowany dodawaniem się mocy szumu kwantowania do mocy sygnału:

6. Wnioski

Zastosowanie cyfrowych metod przetwarzania sygnałów jest wygodną metodą dokonywania pomiarów. Ich niezaprzeczalną zaletą jest uzyskanie bardziej dokładnych wyników pomiarów (związane jest to z mniejszą podatnością sygnału cyfrowego na zakłócenia zewnętrzne). Ponadto metoda ta pozwala na natychmiastowe otrzymanie wyników pomiarów oraz szeregu innych danych dotyczących badanego sygnału obliczanych przez komputer (np. estymatorów, wartości odchylenia średniokwadratowego - zależne od użytego oprogramowania). Możliwe jest także uzyskanie (wykreślanych przez komputer) histogramów, dzięki którym można szybko zorientować się co do przebiegu badanego sygnału. Niestety na wielkość błędu pomiaru ma wpływ duża wartość składowej stałej badanego sygnału, którą nie w każdym przypadku udaje się wyeliminować. Decydujący wpływ na błąd pomiaru ma skończony czas konwersji a/c uniemożliwiający zwiększanie ponad pewną wartość częstotliwości próbkowania, która dla większych wartości pozwala na dokładniejsze odwzorowanie przebiegu sygnału i obliczenia pożądanych parametrów.

Miernictwo Elektroniczne - laboratorium

************************************************************

************************************************************

- 2 -

************************************************************

- 1 -

---