Rok akademicki 1997/98	Laboratorium z fizyki
Nr ćwiczenia: 65	Badanie rozkładu elektronów w zależności od ich prędkości.
Wydział: Elektronika Kierunek: I.K.	TOMASZ SUCHOCKI
Data wykonania 1998-04-03	Ocena		Data zaliczenia	Podpis
	T
	S

1. Zasada Pomiaru

Celem ćwiczenia jest określenie rozkładu termoelektronów w funkcji ich prędkości metodą hamującego potencjału. Badanie rozkładu elektronów w zależności od ich prędkości wykonujemy badając lampę elektronową.

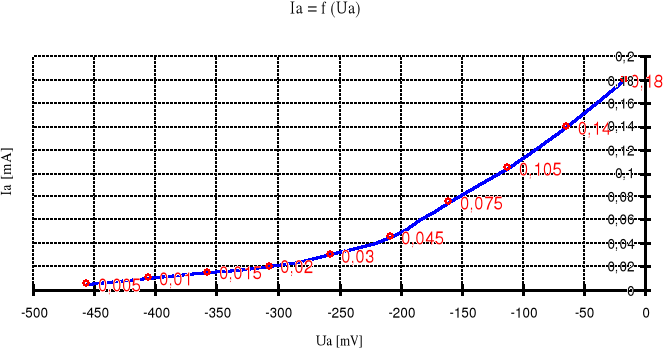
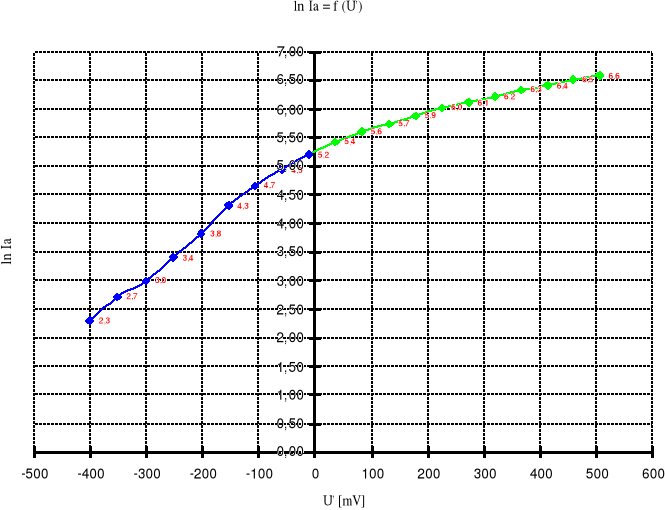
Podając na anodę lampy próżniowej z żarzoną katodą napięcie hamujące przeszkadzające dopływowi elektronów do anody spowodujemy, że to do tej ostatniej dotrą tylko te elektrony, których energia kinetyczna jest większa od pracy sił pola elektrycznego wywołującego hamowanie. Mierząc prąd anody przy różnych napięciach hamowania, można bezpośrednio śledzić ilość termoelektronów zależności od ich energii (prędkości). Rysując wykres ln J_a w funkcji napięcia hamującego powinniśmy otrzymać prostą opisaną równaniem:

, gdzie

J_a0 - wartość natężenia prądu anodowego w przypadku gdy różnica potencjałów między anodą i katodą wynosi zero (U = 0);

U - wartość napięcia hamującego;

k_B - stała Boltzmana;

e - ładunek elementarny;

T - temperatura.

Znając e/k_BT (współczynnik nachylenia prostej) można obliczyć temperaturę odpowiadającą stanowi, w jakim znajduje się gaz elektronowy w lampie (wyznaczając temperaturę gazu elektronowego wyznaczamy temperaturę katody).

Znając wartość napięcia hamującego można określić prędkość elektronów korzystając z zależności:

, gdzie

m - masa elektronu;

v - prędkość elektronu;

e - ładunek elektronu.

2. Schemat Układu Pomiarowego

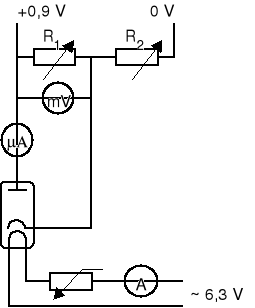
3. Ocena Dokładności Poszczególnych Pomiarów

1. miliwoltomierz:

klasa 0,5 zakres 750 mV

2. mikroamperomierz:

klasa 0,5 zakres 750 A opór wew. Ra = 60

3. amperomierz:

klasa 0,5 zakres 1 A

4.Tabele Pomiarowe

Tabela Pomiarowa Dla Kierunku Przewodzenia:

Lp.	Iz	Ia	U	IaRa	U'=U-IaRa	lnIa	ln(Ia/Io)
	[A]	[A]	[mV]	[mV]	[mV]	[A]	-
1	0,65	720	550	43,2	506,8	6,6	1,39
2	0,65	670	500	40,2	459,8	6,5	1,31
3	0,65	610	450	36,6	413,4	6,4	1,22
4	0,65	555	400	33,3	366,7	6,3	1,13
5	0,65	500	350	30,0	320,0	6,2	1,02
6	0,65	450	300	27,0	273,0	6,1	0,92
7	0,65	405	250	24,3	225,7	6,0	0,81
8	0,65	355	200	21,3	178,7	5,9	0,68
9	0,65	310	150	18,6	131,4	5,7	0,54
10	0,65	270	100	16,2	83,8	5,6	0,41
11	0,65	225	50	13,5	36,5	5,4	0,22
12	0,65	180	0	10,8	-10,8	5,2	-

Tabela Pomiarowa Dla Kierunku Zaporowego:

Lp.	Iz	Ia	U	IaRa	U'=U-IaRa	Ua=U'+	lnIa	ln(Ia/Io)
	[A]	[A]	[mV]	[mV]	[mV]	[mV]	[A]
1	0,65	180	0	10,8	-10,8	-16,9	5,2	-
2	0,65	140	-50	8,4	-58,4	-64,5	4,9	-0,25
3	0,65	105	-100	6,3	-106,3	-112,4	4,7	-0,54
4	0,65	75	-150	4,5	-154,5	-160,6	4,3	-0,88
5	0,65	45	-200	2,7	-202,7	-208,8	3,8	-1,39
6	0,65	30	-250	1,8	-251,8	-257,9	3,4	-1,79
7	0,65	20	-300	1,2	-301,2	-307,3	3,0	-2,20
8	0,65	15	-350	0,9	-350,9	-357,0	2,7	-2,48
9	0,65	10	-400	0,6	-400,6	-406,7	2,3	-2,89
10	0,65	5	-450	0,3	-450,3	-456,4	1,6	-3,58
11	0,65	0	-500	0,0	-500,0	-506,1	-	-

5. Przykładowe Obliczenia

• Obliczenia Dla Kierunku Przewodzenia Dla Pomiaru 3:

a.) Obliczanie wartości napięcia na mikroamperomierzu:

J_aR_a = 610·10^-6 · 60 = 0,0366 V = 36,6 mV

b.) Obliczanie napięcia na diodzie:

U' = U - J_aR_a = 450 - 36,6 = 413,4 mV

• Obliczenia Dla Kierunku Zaporowego Dla Pomiaru 3:

a.) Obliczanie wartości napięcia na mikroamperomierzu:

J_aR_a = 105·10^-6 · 60 = 0,0063 V = 6,3 mV

b.) Obliczanie napięcia na diodzie:

U' = U - J_aR_a = -100 mV - 6,3 mV = -106,3 mV

c.) Obliczanie rzeczywistego napięcia na diodzie (uwzględniając kontaktową różnicę potencjałów):

U_a = U' +  = -106,3 mV + 6,098 mV = - 112,4 mV

• Obliczanie Temperatury Katody:

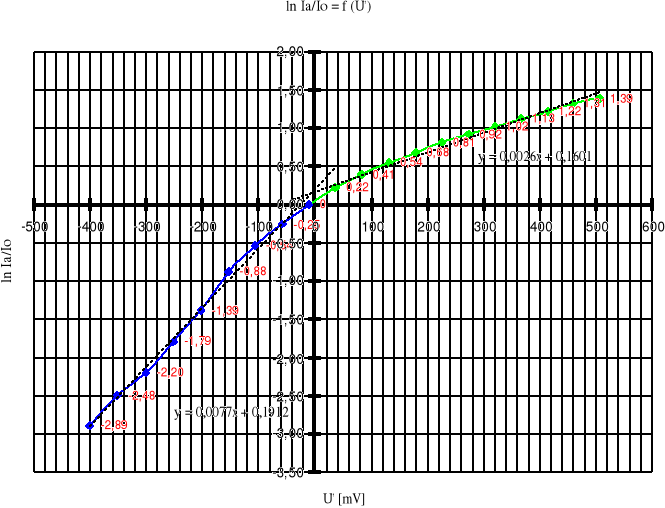
Do obliczeń potrzebna jest wartość tgα, którą obliczę z wykresu:

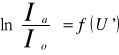
Wykorzystam równanie prostej aproksymującej dla kierunku zaporowego, która pozwoli mi w łatwy sposób obliczyć tgα

y = 0,0077x + 0,2865

Podstawiając za x dowolną wartość, otrzymujemy y (musimy uwzględnić jednostkę):

Ze wzoru obliczam temperaturę katody, dla kierunku zaporowego, wynosi ona: 1,6*10-19/(1,3*10-23*15,5)= 794 K

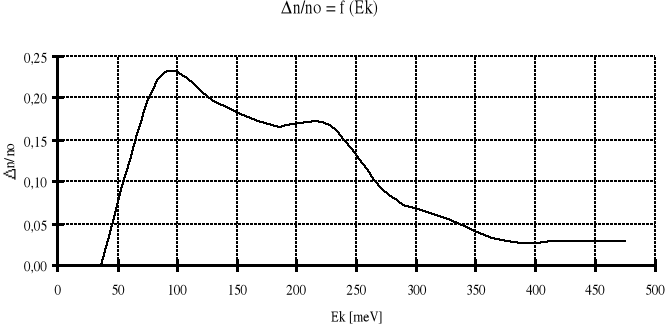
• Obliczanie Względnej Liczby Atomów :

• Obliczanie Energii Kinetycznej:

E_k = /e · U_a /= /-112,4 · 10^-3 / eV ≈ 112 eV

• Obliczanie Prędkości Elektronów:

• Obliczanie Kontaktowej Różnicy Potencjałów Δϕ:

Do obliczeń tych posłużyłem się równaniami prostych aproksymujących z wykresu,

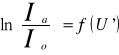
które w miejscu przecięcia się wyznaczyły mi dokładną wartość x, czyli szukane Δϕ.

y = 0,0026x + 0,1601

y = 0,0077x + 0,1912

Δϕ = 6,098 [mV]

6. Zestawienie wyników

LP	dn/no	Ek	V
	-	[meV]	[km/s]
1	0,00	17	77
2	0,22	64	151
3	0,19	112	199
4	0,17	161	238
5	0,17	209	271
6	0,08	258	301
7	0,06	307	329
8	0,03	357	354
9	0,03	407	378
10	0,03	456	400

7. Wnioski i Spostrzeżenia

Doświadczenie to ma charakter statystyczny i cechuje się dużą niedokładnością. Wynika to z tego, że zbadanie E_k i v elektronu jest trudne ze względu na przypadkowy charakter wypływu elektronów z katody. Prędkości te możemy jedynie określić w pewnym przybliżeniu i z dość dużym błędem.

---