Doświadczenie
Wyznaczanie Przyspieszenia ziemskiego za pomocą wahadła matematycznego.
CZĘŚĆ TEORETYCZNA
Wahadłem matematycznym nazywamy ciało o masie m skupionej w jednym punkcie, zawieszonej na nieważkiej nici o stałej długości l.
W praktyce nie jest to możliwe do zrealizowania, gdyż nie istnieje nieważka, nierozciągliwa nić i nie ma ciała, którego masa byłaby skupiona w jednym punkcie. Dobrym przybliżeniem do tego ideału może być metalowa kulka zawieszona na cienkiej, stosunkowo mało rozciągliwej nici.
Wahadło wykonuje ruch drgający. Drgania są w poziomie. Za ruch drgający wahadła matematycznego odpowiada składowa ciężaru ciała.
Okresem tego ruchu, czyli okresem wahań wahadła T , nazywamy czas potrzebny na przebycie przez wahadło drogi od punktu maksymalnego wychylenia poprzez przejście przez punkt równowagi do maksymalnego wychylenia w druga stronę i z powrotem, a wiec czas potrzebny na wykonanie jednego pełnego wahnięcia.
Zachodzi pytanie, czy obserwowany ruch drgający jest ruchem harmonicznym?
Aby się o tym przekonać, należy wyznaczyć przyspieszenie lub siłę w tym ruchu drgającym i sprawdzić, czy jest ona proporcjonalna do wychylenia i zwrócona ku środkowi drgań. W tym celu zbadajmy, jaka siła działa na odchylony punkt materialny o masie m.
rys. 1 Wahadło matematyczne
Wobec tego, że punkt ten znajduje się w polu grawitacyjnym Ziemi działa na niego siła
FF= m * g
*g
gdzie g jest przyspieszeniem ziemskim.
Rozłóżmy siłę F na dwie składowe: siłę F1- działająca w kierunku ruchu, a więc stycznie do nakreślonego okręgu, powodującą badany ruch drgający, oraz siłę F2 w kierunku nici.
Składowa F2 nie wpływa na ruch.
Interesującą nas siłę F1 łatwo wyznaczymy z trójkąta.
Przy niewielkich katach możemy, jak wiadomo, zamiast sinusa kąta wziąć jego miarę łukową. Biorąc pod uwagę wycinek okręgu łatwo znajdziemy, że:
![]()
gdzie l jest długością wahadła. Ponieważ długość łuku niewiele różni się od wychylenia x otrzymamy zatem dla małych kątów , czyli dla małych wychyleń:
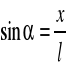
F
Podstawiając do wzoru na F1 i pamiętając, że F= m * g otrzymamy:
![]()
Z wzoru tego widać jasno, że siła powodująca ruch wahadła jest siłą wprost proporcjonalną do wychylenia i zwróconą ku środkowi drgań, z czego wynika, że ruch wahadła dla małych wychyleń można uważać za harmoniczny.
Porównując siłę F1 z ogólna postacią siły w ruchu harmonicznym możemy wyprowadzić wzór na okres wahań wahadła matematycznego.
Patrząc na wzór nasuwają się następujące wnioski:
We wzorze tym nie występuje kąt wychylenia α, zatem okres wahań nie zależy od kąta wychylenia wahadła (jednak wychylenia nie mogą być zbyt wielkie bo takie przyjęliśmy założenia).
We wzorze nie występuje masa wahadła, zatem okres wahań wahadła matematycznego nie zależy od jego masy.
Okres wahań wahadła jest proporcjonalny do pierwiastka kwadratowego z długości wahadła. Oznacza to, że wahadło 4 razy dłuższe ma okres wahań tylko dwukrotnie dłuższy.
Okres wahań wahadła jest odwrotnie proporcjonalny do pierwiastka kwadratowego z przyśpieszenia ziemskiego. Oznacza to, że w miejscowościach na Ziemi bliższych jej biegunów, gdzie przyśpieszenie ziemskie jest nieco większe, okres wahań wahadła powinien być nieco krótszy, a bliżej równika, gdzie przyśpieszenie ziemskie jest nieco mniejsze, okres wahań wahadła powinien być nieco dłuższy.
Dla małych drgań okres drgań
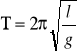
jest niezależny od amplitudy, co nazywamy izochronizmem drgań. Tę właściwość wahadła odkrył włoski fizyk i astronom Galileusz, obserwując wahania żyrandola w katedrze.
Tematem naszego doświadczenia jest wyznaczanie przyspieszenia ziemskiego za pomocą wahadła matematycznego, zatem ze wzoru na okres drgań tego wahadła możemy wyznaczyć wzór na przyspieszenie ziemskie:
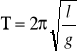
/2
![]()
/*g
![]()
/: T2
![]()
CEL DOŚWIADCZENIA
Wyznaczanie przyspieszenia ziemskiego
ZESTAW DOŚWIADCZALNY:
Wahadło matematyczne (ciężarek, nić)
statyw
stoper
miarka
KOLEJNOŚĆ CZYNNOŚCI:
zawieszamy ciężarek na sznurku
mocujemy sznurek do statywu
mierzymy długość wahadła od punktu mocowania do środka ciężarka na końcu wahadła
odchylamy wahadło o niewielki kąt
mierzymy czas 10 wahnięć
Pomiar powtarzamy 3 razy
zmieniamy długość wahadła raz i powtarzamy pomiary
wyniki pomiarów zamieszczamy w tabeli
TABELA POMIARÓW
Tabela 1.
Lp. |
Długość wahadła L wyrażona w [cm] |
Czas 10 wahnięć T10 |
Czas jednego wahnięcia T |
Przyspieszenie ziemskie
|
1. |
90,5 |
19 |
1,9 |
9,89 |
2. |
91 |
19,1 |
1,91 |
9,86 |
3. |
90,6 |
19,2 |
1,92 |
9,71 |
|
Lśr = 90,7 |
|
Tśr = 1,91 |
gśr = 9,86 |
Tabela 2.
Lp. |
Długość wahadła L wyrażona w [cm] |
Czas 10 wahnięć T10 |
Czas jednego wahnięcia T |
Przyspieszenie ziemskie
|
1. |
75 |
17,4 |
1,74 |
9,78 |
2. |
74,6 |
17,3 |
1,73 |
9,84 |
3. |
75,2 |
17,5 |
1,75 |
9,79 |
|
Lśr = 74,93 |
|
Tśr = 1,74 |
gśr = 9,80 |
DYSKUSJA BŁĘDÓW
OBLICZENIA DLA PIERWSZEJ TABELI POMIAROWEJ:
0,305
1,327
Analiza błędu:
Otrzymany wynik mieści się w granicy błędu, jednakże do otrzymanego błędu mogło się przyczynić:
niedokładność przyrządu pomiarowego przy pomiarze długości wahadła
niedokładność pomiaru czasu 10 wahnięć wahadła
Porównanie otrzymanego wyniku z wartością tablicową
Z tablic fizycznych odczytałem, że przyspieszenie standardowe siły ciężkości g wynosi 9,81 m/s2. Ja uzyskałam wynik 9,86 m/s2.![]()
OBLICZENIA DLA DRUGIEJ TABELI POMIAROWEJ:
0,2
0,0615
Analiza błędu:
Otrzymany wynik mieści się w granicy błędu, jednakże do otrzymanego błędu mogło się przyczynić:
niedokładność przyrządu pomiarowego przy pomiarze długości wahadła
niedokładność pomiaru czasu 10 wahnięć wahadła
Porównanie otrzymanego wyniku z wartością tablicową
Z tablic fizycznych odczytałem, że przyspieszenie standardowe siły ciężkości g wynosi 9,81 m/s2. Ja uzyskałam wynik 9,86 m/s2.![]()
WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA MATEMATYCZNEGO
13 | Strona
g = 9,81 m/s2
Wartość Tablicowa 9.81
8,53 9,86 11,187
Wartość Tablicowa 9.81
9,73 9,80 9,86
Wyszukiwarka