WYKŁAD 5:

LINIE PIERWIASTKOWE JAKO PODSTAWA ANALIZY UKŁADU STEROWANIA

SYNTEZA STEROWNIKÓW:

METODA LINII PIERWIASTKOWYCH

1 Metoda linii pierwiastkowych: analiza

1.1 Układ zamknięty

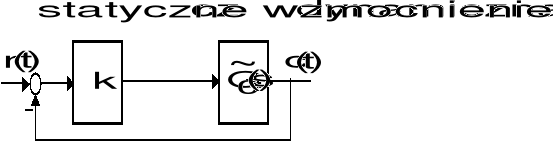
Podstawowy strukturalny schemat układu sterowania

Wzmocnienie statyczne
.

Część dynamiczna układu sterowania
obejmuje obiekt sterowania oraz dynamiczne 'fragmenty' sterownika.

Transmitancja układu otwartego:
.

Transmitancja układu zamkniętego:

.

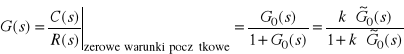
Układ zamknięty będzie stabilny w sensie BIBO (Bounded-Input-Bounded-Output), gdy

wszystkie bieguny transmitancji
leżą w lewej otwartej półpłaszczyźnie

płaszczyzny zespolonej.

Innymi słowy, zera mianownika
, czyli zera wyrażenia
, muszą posiadać

ujemne części rzeczywiste.

Linie pierwiastkowe: miejsce geometryczne zer wyrażenia
przy
.

1.2 Reguły wykreślania linii pierwiastkowych

Podane niżej praktyczne wskazania (reguły) wynikają bezpośrednio z równania

,

które dla danego
musi spełniać zespolona liczba
, aby być pierwiastkiem (miejscem zerowym) mianownika transmitancji
. Równanie powyższe zapisać można w postaci dwóch warunków:

- warunek amplitudowy:
,

- warunek fazowy:
,
.

Reguły:

(1) Linie pierwiastkowe są symetryczne względem osi rzeczywistej płaszczyzny zespolonej.

(2) Linie pierwiastkowe zaczynaja się (dla
) w biegunach transmitancji
, zaś kończą się (dla
) w zerach transmitancji
, włączając zera w nieskończoności.

(3) Linie pierwiastkowe posiadają asymptoty o następujących własnościach:

asymptoty, w liczbie
, są półprostymi wychodzącymi z punktu
(centroid) na

osi rzeczywistej,

liczba biegunów
liczba skończonych zer
, czyli

stopień mianownika
stopień licznika
,

,

kąty między asymptotami a osią rzeczywistą:

,
.

(4) Linie pierwiastkowe na osi rzeczywistej mogą leżeć tylko na lewo od nieparzystej liczby punktów kontrolnych (zer i biegunów transmitancji
).

(5) Punkty wspólne gałęzi linii pierwiastkowych (punkty spotkana oraz punkty rozejścia linii pierwiastkowych - co odpowiada wielokrotnym biegunom transmitancji
) należą do zbioru rozwiązań równania

,

gdzie

,

zaś przez
oraz
oznaczono pochodne odpowiednich wielomianów licznika i mianownika transmitancji
.

(6) Kąt odejścia
linii pierwiastkowej od danego zespolonego bieguna
transmitancji
dany jest wzorem

,
,

gdzie
(
) reprezentuje argument wektora poprowadzonego od bieguna
(zera
) do bieguna
tej transmitancji.

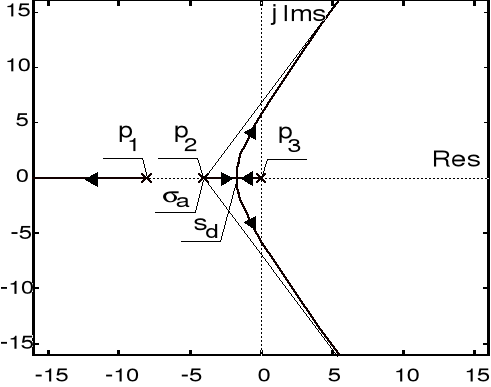
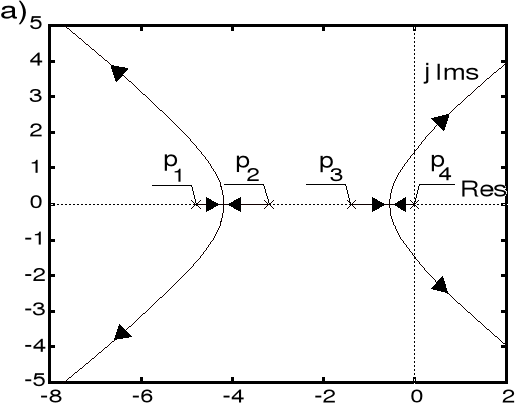
Przykład 1 (linie pierwiastkowe)

Operatorowa transmitancja otwartego układu sterowania z jednostkowym ujemnym sprzężeniem zwrotnym dana jest wzorem

,
.

Podaj obraz linii pierwiastkowych układu zamkniętego, a na tej podstawie określ wzmocnienie
układu na granicy stabilności oraz odpowiadającą temu pulsację drgań nietłumionych.

Rozwiązanie

Niech
oznacza liczbę skończonych zer transmitancji układu otwartego
, zaś
- liczbę jej biegunów. Rozważana transmitancja
nie ma skończonych zer, to znaczy
, a liczba jej biegunów wynosi
. Są to
,
,
. Liczba asymptot, do których dążą linie pierwiastkowe
. Kąty między asymptotami wynoszą
; odpowiednio kąty między asymptotami a osią rzeczywistą są równe
,
. Odciętą
punktu na osi rzeczywistej, z którego wychodzą asymptoty, obliczamy ze wzoru
. Wspólną część linii pierwiastkowych oraz rzeczywistej osi płaszczyzny zespolonej stanowi prawostronnie domknięta półprosta leżąca w lewo od bieguna
oraz domknięty odcinek pomiędzy biegunami
i
. Wynika stąd, iż punkt "odejścia" linii pierwiastkowych od osi rzeczywistej należy do odcinka wyznaczonego biegunami
i
. Współrzędną tego punktu znajdujemy na podstawie charakterystycznego równania układu zamkniętego, wyznaczając maksymalną wartość parametru k, dla której bieguny układu zamkniętego są rzeczywiste. Charakterystyczny wielomian
rozważanego układu ma postać
. Załóżmy, iż
jest pierwiastkiem tego wielomianu. Charakterystyczne równanie
interpretować można jako zapis uwikłanego odwzorowania
, przyporządkowującego danemu pierwiastkowi
taką wartość
, dla której zachodzi
. Różniczkując to uwikłane odwzorowanie, mamy

.

Przyrównując powyższą pochodną do zera, otrzymujemy kwadratowe równanie
o następujących pierwiastkach:
oraz
, z których pierwszy wyznacza szukany punkt odejścia
. Zachodzi bowiem
. Podstawiając
w równaniu
, otrzymujemy odpowiadającą temu punktowi wartość
parametru
:
. Krytyczną wartość
parametru
, przy której układ zamknięty osiąga granicę stabilności, obliczyć można na podstawie równania charakterystycznego
, kładąc
. Uzyskujemy ten sposób równanie
, gdzie
jest pulsacją drgań nietłumionych. Przyrównując do zera urojoną część wyrażenia po lewej stronie rozważanego równania, otrzymujemy, iż
. Z kolei, podstawiając
do równania powstającego z przyrównania do zera rzeczywistej części wyrażenia tworzącego lewą stronę tego równania, wyznaczamy
. Uzyskany w ten sposób obraz linii pierwiastkowych pokazano na poniższym rysunku.

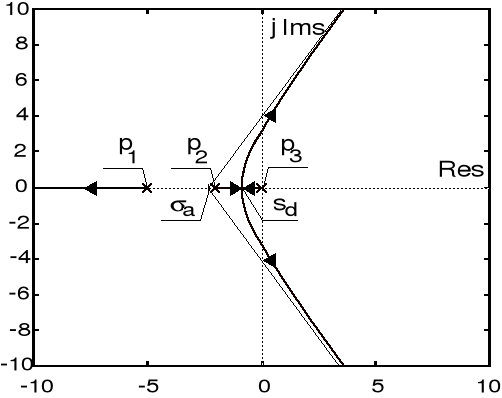
Linie pierwiastkowe

Przykład 2 (linie pierwiastkowe)

Operatorowa transmitancja otwartego układu sterowania z jednostkowym ujemnym sprzężeniem zwrotnym dana jest wzorem

,
.

Podaj obraz linii pierwiastkowych układu zamkniętego, określ wzmocnienie układu otwartego na granicy stabilności oraz odpowiadającą temu pulsację drgań nietłumionych.

Rozwiązanie

Transmitancja otwartego układu nie posiada skończonych zer, to znaczy
, zaś jej biegunami są liczby:
,
oraz
, co oznacza, że
. Wynika stąd, iż spodziewać się należy analogicznego obrazu linii pierwiastkowych jak w Przykładzie 1. Postępując według przyjętego tam schematu, stwierdzamy najpierw, że linie pierwiastkowe dążą ku trzem asymptotom (
) o kątach:
oraz
; punktem wspólnym owych asymptot jest punkt
. Wspólna część linii pierwiastkowych oraz rzeczywistej osi płaszczyzny zespolonej obejmuje zatem półprostą na lewo od bieguna
oraz domknięty odcinek pomiędzy biegunami
i
. Alternatywny do podanego w poprzednim przykładzie sposób wyznaczania punktów odejścia linii pierwiastkowych z (lub pojawienia się na) osi rzeczywistej polega na rozwiązaniu równania
, w którym
oznacza licznik transmitancji
, zaś
- mianownik. Równanie to łatwo jest wyprowadzić, jeżeli zauważy się, iż punkty odejścia oraz punkty pojawienia się linii pierwiastkowych odpowiadają wielokrotnym pierwiastkom charakterystycznego równania układu zamkniętego. W rozważanym przypadku równanie
przyjmuje postać
. Spośród dwóch jego rozwiązań:
oraz
, jako punkt odejścia wybieramy punkt
. Krytyczną wartość
parametru
obliczamy, posługując się kryterium Routha. Na podstawie charakterystycznego równania układu zamkniętego
, otrzymujemy następującą tablicę Routha

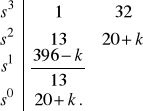
Układ zamknięty jest zatem stabilny przy
. Uwzględniając założenie
, stwierdzamy, że układ zamknięty znajduje się na granicy stabilności, gdy
. Pulsację nietłumionych drgań
wyznaczamy w oparciu o pomocniczy wielomian
. Sprawdźmy jeszcze amplitudowy warunek:
.

Przykład 3 (linie pierwiastkowe)

Operatorowa transmitancja otwartego układu sterowania z jednostkowym ujemnym sprzężeniem zwrotnym dana jest wzorem

,
.

Wyznacz przebieg linii pierwiastkowych układu zamkniętego. Przy jakiej wartości parametru k układ ten osiąga granicę stabilności? Dla jakiej wartości k transmitancja układ zamknięty ma podwójny biegun w punkcie
?

Rozwiązanie

Na podstawie powyższego wzoru stwierdzamy, iż transmitancja układu otwartego nie posiadając skończonych zer (
) ma cztery (
) bieguny:
oraz
. Linie pierwiastkowe układu zamkniętego dążą zatem ku czterem asymptotom o kątach
i
. Początkowym punktem owych asymptot jest
. Stwierdzamy następnie, iż ten fragment linii pierwiastkowych, w którym przebiegają one wzdłuż osi rzeczywistej, zajmuje odcinek pomiędzy punktami 0 i
. Wynika stąd, iż oczekiwać możemy dwóch punktów odejścia linii pierwiastkowych od tej osi. Punkty odejścia wyznaczamy rozwiązując równanie
, przy czym
, zaś
. Rozważane równanie przyjmuje zatem postać
, z której otrzymujemy punkty odejścia
oraz
. Zachodzi ponadto
(por. poniższy rysunek).

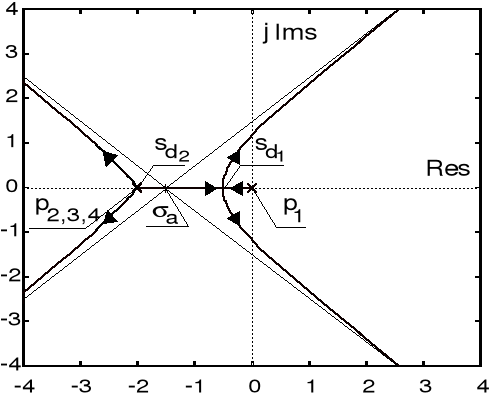
Linie pierwiastkowe

Krytyczną wartość
parametru
, przy której układ zamknięty znajduje się na granicy stabilności, wyznaczymy na podstawie równania charakterystycznego tego układu:
. Analizując pierwszą kolumnę tablicy Routha skojarzonej z tym równaniem, stwierdzamy, iż zamknięty układ jest stabilny przy
. Pulsację nietłumionych drgań
dla krytycznej wartości
wyznaczyć można w oparciu o pomocnicze równanie uzyskane z badanej tablicy Routha:
. A zatem
. Dla podwójnego bieguna
mamy
.

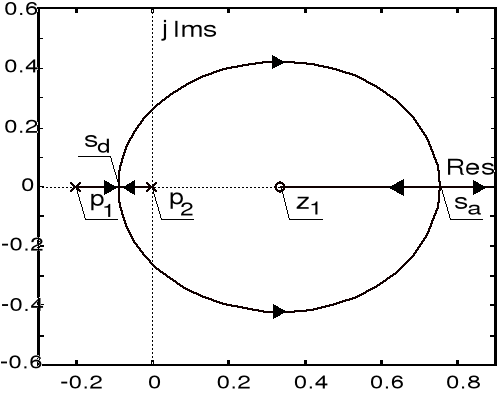
Przykład 4 (linie pierwiastkowe - zadanie niestandardowe)

Rozważmy układ sterowania pokazany na rysunku niżej.

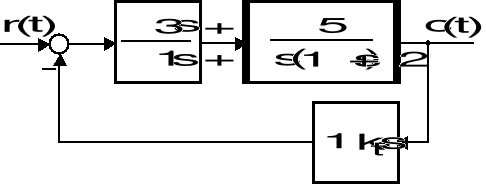
Strukturalny schemat układu sterowania

W oparciu o metodę linii pierwiastkowych wyznacz położenie pierwiastków równania charakterystycznego tego układu w zależności od współczynnika prędkościowego sprzężenia
. Dla jakich wartości tego współczynnika skokowa odpowiedź rozważanego układu charakteryzuje się czasem ustalania
nie przekraczającym 3 s?

Rozwiązanie

Równanie charakterystyczne rozważanego układu sterowana ma postać określoną wzorem
. Metodę linii pierwiastkowych należy przeto zastosować do następującej pomocniczej transmitancji operatorowej

.

Transmitancja ta posiada trzy bieguny:
i
oraz dwa skończone zera:
i
. Stwierdzamy następnie, iż obszar, w którym linie pierwiastkowe leżą na rzeczywistej osi płaszczyzny zespolonej ma postać sumy dwóch przedziałów
. Na podstawie dotychczasowych ustaleń łatwo dojść do wniosku, że w obrazie linii pierwiastkowych, składającym się z trzech gałęzi, dwie z tych gałęzi dążą ku zerom
i
, trzecia zaś gałąź dąży wzdłuż osi odciętych do
. Wyznaczając punkty pojawienia się linii pierwiastkowych na osi odciętych posługujemy się równaniem
, które, jak łatwo sprawdzić, przyjmuje tu postać daną wzorem:
. Spośród pierwiastków tego równania:
,
oraz
,
jest poszukiwanym punktem pojawienia się:
. Kąt odejścia
od bieguna zespolonego
obliczamy na podstawie wzoru
, gdzie
,
,
oraz
. Wynika stąd, iż
. Wartości współczynnika
, przy których zamknięty układ zachowuje stabilność, wyznaczyć można na podstawie analizy tablicy Routha odpowiadającej rozważanemu równaniu charakterystycznemu. Tak postępując, stwierdzamy, iż układ sterowania jest układem stabilnym dla
. Krytycznej wartości
odpowiada para urojonych biegunów
transmitancji układu sterowania. Przebieg linii pierwiastkowych przedstawiono na poniższym rysunku.

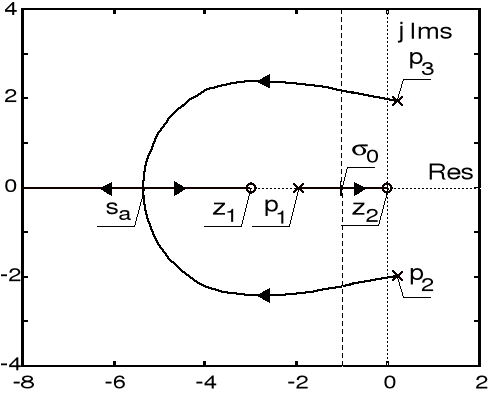
Linie pierwiastkowe układu sterowania

Załóżmy, że wartość czasu ustalania
skokowej odpowiedzi stabilnego układu zamkniętego oszacować można w oparciu o wzór
, gdzie
oznacza część rzeczywistą tego pierwiastka równania charakterystycznego, który leży najbliżej osi urojonej. Dla
otrzymujemy
. Dokonując w równaniu charakterystycznym
następującego podstawienia (transformacji zmiennych)
, otrzymujemy zmodyfikowaną tablicę Routha, z której wynika, iż dla
pierwiastki rozważanego równania charakterystycznego mają części rzeczywiste mniejsze niż
. Przykładowo, dla
zachodzi
.

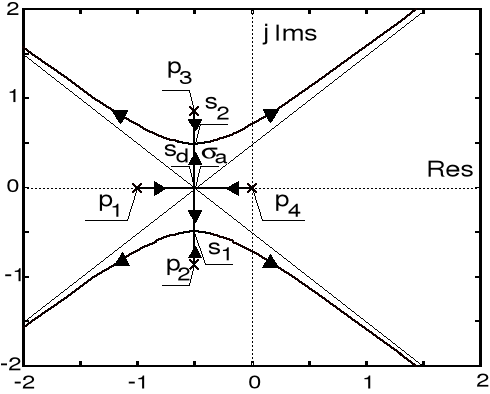
Przykład 5 (linie pierwiastkowe)

Operatorowa transmitancja otwartego układu sterowania z jednostkowym ujemnym sprzężeniem zwrotnym dana jest wzorem

.

Jest więc to układ niestabilny w stanie otwartym. Wyznaczając obraz linii pierwiastkowych układu zamkniętego, zbadaj możliwość ustabilizowania tego układu poprzez odpowiedni dobór wartości parametru
.

Rozwiązanie

Stosując rutynową procedurę, znajdujemy kolejno:

1. Bieguny transmitancji układu otwartego:
,
oraz
.

2. Skończone zero tej transmitancji:
.

3. Trzy asymptoty o kątach
oraz
z początkiem w punkcie
.

4. Stwierdzamy następnie, iż linie pierwiastkowe zajmują na osi rzeczywistej obszar stanowiący sumę dwóch przedziałów
oraz
.

5. Obraz linii pierwiastkowych składa się z czterech gałęzi, należy zatem oczekiwać jednego odejścia od osi rzeczywistej i jednego pojawienia się na tej osi. Rozwiązując równanie
, które przyjmuje teraz postać
, uzyskujemy pierwiastki:
,
oraz
. Punkt
jest punktem pojawienia się, podczas gdy
jest punktem odejścia linii pierwiastkowych.

6. Wyznaczmy kąt odejścia linii pierwiastkowej od bieguna zespolonego
. Mamy (zob. rysunek):
,
,

oraz
. Zatem kąt odejścia linii pierwiastkowej od bieguna
wynosi
. Przebieg linii pierwiastkowych zobrazowano na poniższym rysunku.

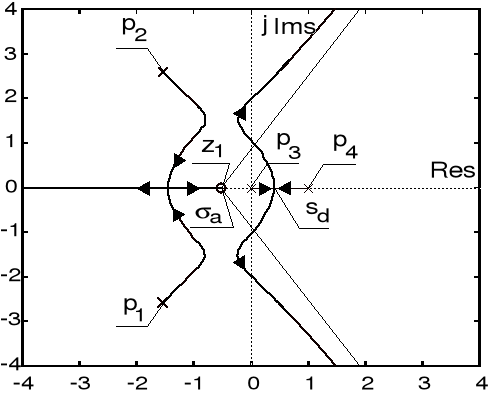
Linie pierwiastkowe

7. Przedział wartości
stabilizujących zamknięty układ sterowania wyznaczamy na podstawie tablicy Routha, otrzymanej w oparciu o charakterystyczne równanie tego układu:
. Tak postępując, ustalono, iż układ zachowuje stabilność przy

. Z tablicy tej otrzymujemy także punkty przecięcia linii pierwiastkowych z urojoną osią płaszczyzny zespolonej (co odpowiada układowi zamkniętemu na granicy stabilności): dla
są to punkty
, zaś dla
są to punkty
.

8. Transmitancja zamkniętego układu sterowania ma podwójne rzeczywiste bieguny
oraz
przy wzmocnieniu
równym, odpowiednio:
oraz
.

Zadania do samodzielnego rozwiązania

Zadanie 1

Operatorowa transmitancja otwartego układu sterowania z jednostkowym ujemnym sprzężeniem zwrotnym ma postać
,
. Podaj obraz linii pierwiastkowych zamkniętego układu; określ krytyczną wartość parametru
, przy której układ ten osiąga granicę stabilności oraz oszacuj pulsację drgań nietłumionych .

Odpowiedź

Obraz linii pierwiastkowych rozważanego układu pokazany jest na rysunku danym niżej. Wspólnym punktem trzech asymptot jest
. Kąty między asymptotami a osią rzeczywistą wynoszą
i
. Punktem odejścia linii pierwiastkowych od tej osi jest
, czemu odpowiada parametr
. Obszar na osi rzeczywistej zajmowany przez linie pierwiastkowe określony jest jako
. Zamknięty układ osiąga granicę stabilności w przypadku, gdy
; odpowiadająca temu pulsacja drgań wynosi
.

Linie pierwiastkowe

Zadanie 2

Operatorowa transmitancja otwartego układu sterowania z jednostkowym ujemnym sprzężeniem zwrotnym dana jest wzorem
,
. Podaj obraz linii pierwiastkowych zamkniętego układu; wyznacz taką wartość parametru
, przy której skokowa odpowiedź tego układu jest krytycznie tłumiona.

Odpowiedź

Odpowiedź zamkniętego układu jest krytycznie tłumiona przy
(operatorowa transmitancja tego układu posiada wówczas podwójny biegun
, odpowiadający punktowi pojawienia się linii pierwiastkowych na osi rzeczywistej). Obszar na osi rzeczywistej zajmowany przez linie pierwiastkowe to półprosta
. Kąt odejścia linii pierwiastkowej od bieguna
ma wartość
.

Zadanie 3

Operatorowa transmitancja otwartego układu sterowania z jednostkowym ujemnym sprzężeniem zwrotnym ma następującą postać
,
. Wyznacz obraz linii pierwiastkowych układu zamkniętego; określ przedział wartości parametru
, którym odpowiada stabilny układ zamknięty; oblicz pulsację drgań na granicy stabilności.

Odpowiedź

Obraz linii pierwiastkowych pokazany jest na poniższym rysunku, przy czym:

- obszar odpowiadający położeniu linii pierwiastkowych na osi rzeczywistej stanowi sumę dwóch przedziałów

,

- punkt odejścia linii pierwiastkowych od osi rzeczywistej
(osiągany przy
),

- punkt pojawienia się linii pierwiastkowych na osi rzeczywistej
(odpowiadający
),

- układ zamknięty jest stabilny dla
, zaś pulsacja drgań na granicy stabilności (przy
) wynosi
.

Linie pierwiastkowe

Zadanie 4

Operatorową transmitancję otwartego układu sterowania z jednostkowym ujemnym sprzężeniem zwrotnym określa wzór
, przy czym
. Wyznacz obraz linii pierwiastkowych układu zamkniętego.

Odpowiedź

Przebieg linii pierwiastkowych pokazano na poniższym rysunku, przy czym:

- linie pierwiastkowe dążą do dwóch asymptot przecinających oś rzeczywistą pod kątami
w punkcie
,

- punktem odejścia linii pierwiastkowych od osi rzeczywistej jest
,

- kąt odejścia od bieguna
ma wartość
,

- kąt dojścia linii pierwiastkowej do zera
ma wartość
,

- układ zamknięty jest stabilny przy
, dla
układ znajduje się na granicy stabilności (linie pierwiastkowe przecinają wówczas oś urojoną w punktach
).

Przebieg linii pierwiastkowych układu sterowania

Zadanie 5

Operatorowa transmitancja pewnego otwartego układu sterowania z jednostkowym ujemnym sprzężeniem zwrotnym ma postać
,
. Wyznacz przebieg linii pierwiastkowych układu zamkniętego.

Odpowiedź

Przebieg linii pierwiastkowych rozważanego układu zamkniętego pokazany jest na rysunku

Linie pierwiastkowe układu sterowania

Przebieg ten odpowiada następującym szczegółowym ustaleniom:

- linie pierwiastkowe dążą do czterech asymptot, które przecinają oś rzeczywistą pod kątami
oraz
w punkcie
(punkt ten jest także punktem odejścia linii pierwiastkowych od osi rzeczywistej:
),

- linie pierwiastkowe zajmują na osi rzeczywistej przedział
,

- kąt odejścia linii pierwiastkowej od bieguna
ma wartość
,

- układ zamknięty jest stabilny przy
, dla
układ znajduje się na granicy stabilności, zaś pulsacja drgań wynosi
,

- równanie
ma trzy pierwiastki:
oraz
, przy czym punkty
odpowiadają podwójnym biegunom zespolonym transmitancji układu zamkniętego, osiąganym przy
, zaś punkt
, odpowiada podwójnemu rzeczywistemu biegunowi tej transmitancji, osiąganemu przy
.

Zadanie 6

Transmitancja otwartego układu sterowania z jednostkowym ujemnym sprzężeniem zwrotnym ma postać
,
. Wyznacz przebieg linii pierwiastkowych układu zamkniętego, przyjmując kolejno
oraz
.

Odpowiedź

Obraz linii pierwiastkowych zamkniętego układu sterowania pokazany jest na poniższych rysunkach.

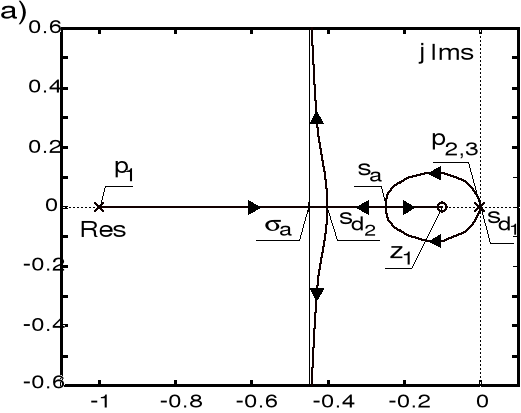
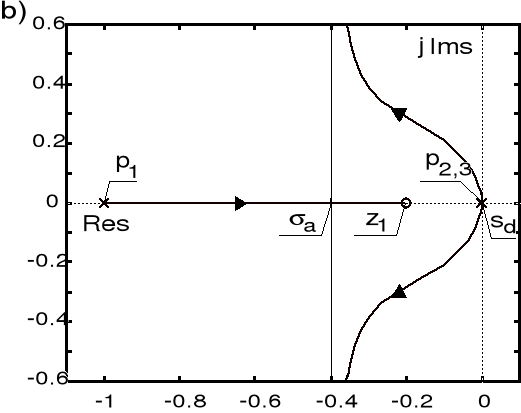
Linie pierwiastkowe układu sterowania: a)
, b)

W obu przypadkach układ zamknięty jest układem stabilnym dla
, gdy
linie pierwiastkowe dążą do zer w nieskończoności wzdłuż asymptot przecinających ujemną półoś rzeczywistą pod kątami
. W przypadku
mamy:

- wspólnym punktem asymptot jest
,

- obszar zajmowany przez linie pierwiastkowe na osi rzeczywistej ma postać zbioru
,

- punkty odejścia linii pierwiastkowych od osi rzeczywistej:
(dla
) oraz
(dla
), zaś punktem powrotu linii pierwiastkowych na oś rzeczywistą jest
(co odpowiada
).

Dla
zachodzi:

- punkt
jest wspólnym punktem asymptot,

- zbiór
określa obszar zajmowany przez linii pierwiastkowe na osi rzeczywistej,

- jedynym punktem odejścia linii pierwiastkowych od osi rzeczywistej jest
.

2 Metoda linii pierwiastkowych: synteza

Przykład 6 (sterownik proporcjonalny)

Obiekt o operatorowej transmitancji danej wzorem

sterowany jest przy pomocy proporcjonalnego sterownika w układzie zamkniętym z jednostkowym ujemnym sprzężeniem zwrotnym. Należy dobrać wzmocnienie
tego sterownika, przy którym skokowa odpowiedź układu zamkniętego charakteryzuje się przeregulowaniem
oraz czasem ustalania
.

Rozwiązanie

Zadanie rozwiązano przybliżoną metodą opartą na analizie obrazu linii pierwiastkowych zamkniętego układu sterowania, odpowiadającego następującej transmitancji układu otwartego
,
. Obraz linii pierwiastkowych pokazano na rysunku, przy czym przez
,
,
oraz
oznaczono bieguny transmitancji
sterowanego obiektu, zaś
jest zerem tej transmitancji.

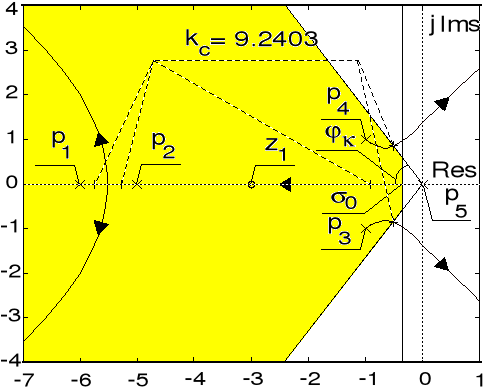
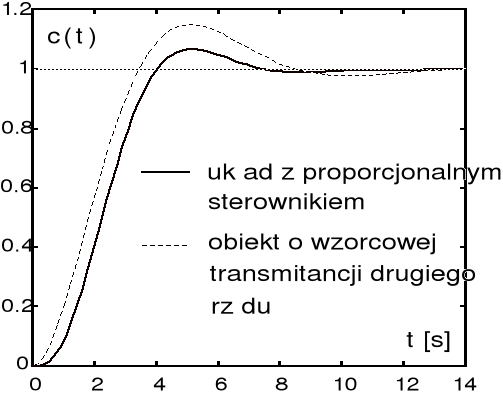
Linie pierwiastkowe Odpowiedzi skokowe

Z rysunku tego wynika, iż istnieje taki przedział dodatnich wartości wzmocnienia
sterownika, któremu odpowiada stabilny układ zamknięty. Krytyczną wartość
tego parametru, przy której układ sterowania znajduje się na granicy stabilności, wyznaczono na podstawie kryterium Routha. Poszukując wzmocnienia
, przy którym odpowiedź układu zamkniętego spełnia postawione wymagania, posłużymy się uproszczoną procedurą, opartą na założeniu, iż o własnościach tego układu decyduje para sprzężonych biegunów, położonych na płaszczyźnie zespolonej w obszarze określonym owymi wymaganiami. W przypadku rozważanych wskaźników
i
odpowiedzi skokowej, obszar taki definiuje się jako wspólną część półpłaszczyzny leżącej na lewo od półprostej
oraz obszaru wyznaczonego kątami
oraz
, przy czym
oraz
, gdzie
, zaś
oznacza unormowany czas ustalania odpowiedzi skokowej członu dynamicznego drugiego rzędu o współczynniku tłumienia
. Podstawiając numeryczne dane niniejszego przykładu (
oraz
), otrzymujemy:
oraz
, czemu odpowiadają wartości
oraz
. Posługując się zleceniem root programu CC, wyznaczono przykładową wartość wzmocnienia sterownika
, przy której wszystkie bieguny transmitancji projektowanego układu sterowania leżą w dopuszczalnym obszarze płaszczyzny zespolonej. Skokowa odpowiedź tak uzyskanego układu charakteryzuje się przeregulowaniem
oraz czasem ustalania
. Na powyższym rysunku pokazano przebieg tej odpowiedzi oraz dla porównania przebieg odpowiedzi wzorcowego członu drugiego rzędu o parametrach
i
.

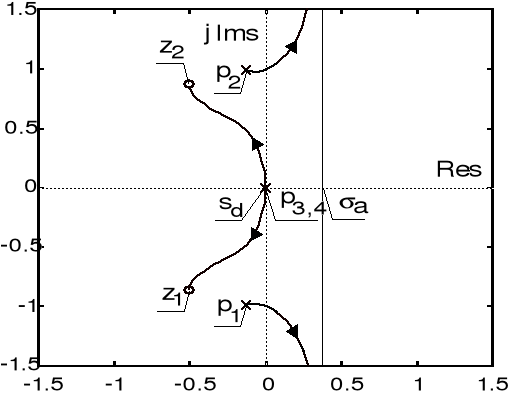
Przykład 7 (sterownik PD)

Dany jest model sterowanego obiektu

.

Określ wartości parametrów k oraz z transmitancji sterowników PD, odpowiednio - idealnego (nierealizowalnego):
,
, oraz rzeczywistego (realizowalnego):
,
, zapewniające operatorowej transmitancji zamkniętego układu sterowania z jednostkowym ujemnym sprzężeniem zwrotnym parę dominujących biegunów
, wynikających z następujących wymagań dotyczących skokowej odpowiedzi tego układu: przeregulowania
oraz czasu ustalania
.

Rozwiązanie

W przypadku sterownika
transmitancja otwartego układu sterowania ma postać

.

Niech
będzie przyjętym do rozważań dominującym biegunem transmitancji zamkniętego układu sterowania. Z fazowego warunku
,
, otrzymujemy równanie
, w którym
jest przyczynkiem kątowym zależnym od parametru
transmitancji sterownika, zaś
,
i
oznaczają przyczynki kątowe pochodzące od odpowiednich biegunów
,
oraz
transmitancji sterowanego obiektu (por. rys. niżej). Zachodzi zatem
, skąd wynika poszukiwana wartość parametru z sterownika o transmitancji
:
. Wartość parametru k tego sterownika oblicza się z amplitudowego warunku
, mamy przeto
.

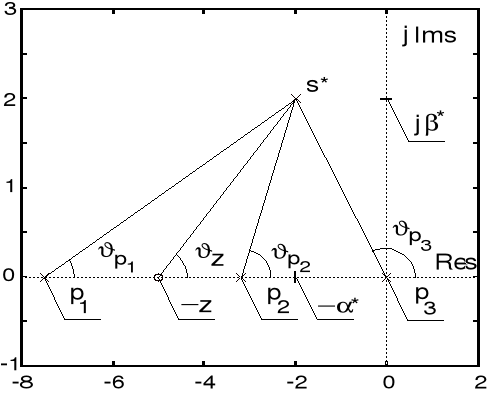
Przyczynki fazowe odpowiadające transmitancji układu otwartego

Rozważając zastosowanie sterownika o transmitancji
, w bilansie przyczynków fazowych uwzględnić należy ujemne przesunięcie fazowe
wprowadzane przez odległy biegun
tej transmitancji dla
:
, gdzie
. Ponieważ transmitancja sterownika powinna dla
wnosić do bilansu kątów fazowych dodatni przyczynek o wartości
, zatem w przypadku transmitancji
musi zachodzić
, co prowadzi do kwadratowego równania
, z którego otrzymujemy poszukiwaną wartość parametru z transmitancji transmitancji
:
. Wartość wzmocnienia k wyznaczamy podobnie jak poprzednio z amplitudowego warunku
. Na rysunku a pokazano obraz linii pierwiastkowych odpowiadających sterowanemu obiektowi, z kolei na rysunku b przedstawiono obraz linii pierwiastkowych układu złożonego z tego obiektu oraz zaprojektowanego sterownika PD. Odpowiedzi skokowe rozważanych układów sterowania charakteryzują się następującymi wskaźnikami: w przypadku idealnego sterownika PD zachodzi
oraz
, zaś dla sterownika rzeczywistego uzyskano
oraz
.

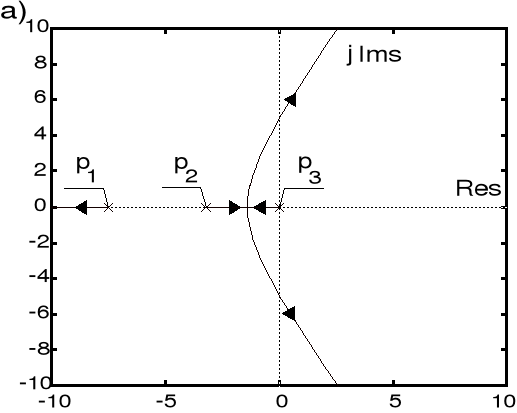
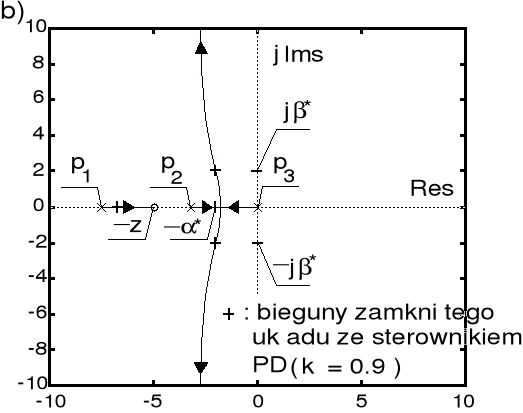
Obraz linii pierwiastkowych układu sterowania:

a) układ bez sterownika, b) układ ze sterownikiem PD

Przykład 8 (sterownik PID - wzory ogólne)

Rozważmy układ sterowania z jednostkowym ujemnym sprzężeniem zwrotnym złożony z obiektu o operatorowej transmitancji
oraz sterownika PID o idealizowanej transmitancji operatorowej

.

Sformułuj warunki jakie muszą spełniać parametry
,
oraz
tego sterownika, aby charakterystyczne równanie rozważanego zamkniętego układu sterowania posiadało parę pierwiastków zespolonych sprzężonych o zadanych wartościach (
) .

Rozwiązanie

Przyjmijmy następujące oznaczenia:
oraz
.Ponieważ sterownik ten charakteryzuje się trzema stopniami swobody, zatem jeden z jego parametrów uczynić można parametrem swobodnym - co pozwoli na odpowiednią parametryzację rodziny rozwiązań. Okazuje się, iż jako swobodny parametr dogodnie jest przyjąć stałą całkowania
, co prowadzi do następującego układu liniowych równań na wartości pozostałych parametrów
oraz

,

.

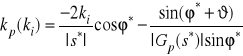
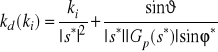
Parametr
wyznaczyć można na podstawie dodatkowego wymagania nałożonego na projektowany układ sterowania - w szczególności dotyczy to zakładanej statycznej dokładności tego układu (odpowiednie wymaganie przyjmuje postać żądania określonej wartości wzmocnienia prędkościowego lub przyspieszeniowego tego układu).

W przypadku sterownika PD należy przyjąć
, co prowadzi do następujących zależności:

,

.

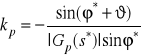
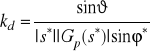
W przypadku sterownika PI nastawę
uzyskuje się z warunku
, skąd otrzymujemy

.

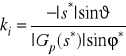
Przykład 9 (sterownik PID)

Obiekt o operatorowej transmitancji

jest sterowany za pomocą sterownika PID o transmitancji
w układzie z jednostkowym ujemnym sprzężeniem zwrotnym. Wyznacz takie wartości parametrów
,
oraz
tego sterownika, aby zapewnić układowi zamkniętemu czas ustalania odpowiedzi skokowej
, zapas fazy
oraz wzmocnienie przyspieszeniowe
.

Rozwiązanie

Załóżmy, iż dynamiczne własności rozważanego zamkniętego układu sterowania zdeterminowane są parą (
) dominujących zespolonych sprzężonych biegunów transmitancji operatorowej tego układu. Część rzeczywistą i urojoną tych biegunów (
) wyznaczamy na podstawie wymagań stawianych rozważanemu układowi. W tym celu korzystamy ze wzorów:
oraz
, przy czym współczynnik tłumienia
obliczamy na podstawie założonego zapasu stabilności,
, zaś parametr
skali czasu wyznaczyć możemy w oparciu o przybliżony wzór
, bądź też stosując dokładną zależność
, w której przez
oznaczono unormowaną wartość czasu ustalania odpowiedzi skokowej członu dynamicznego drugiego rzędu, zależną od współczynnika tłumienia
i szacowaną na drodze numerycznej (symulacyjnej). Przyspieszeniowe wzmocnienie projektowanego układu sterowania określone jest wzorem
. Zgodnie z narzuconymi wymaganiami mamy
, czemu odpowiada unormowany czas ustalania
. Na tej podstawie wyznaczamy
, a następnie dominujący biegun
, gdzie
oraz
. Ponieważ
, a zatem
. Dla
zachodzi przeto
oraz
, czemu odpowiada
oraz
. Parametry
i
sterownika wyznaczamy zagodnie z metodą podaną w Przykładzie 8, otrzymując

,

.

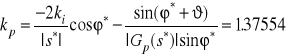
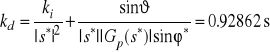
Symulacyjna weryfikacja własności tak uzyskanego układu sterowania prowadzi do następujących oszacowań wskaźników odpowiedzi skokowej: czas ustalania
oraz przeregulowanie
(zauważmy, iż założonemu współczynnikowi tłumienia
przyporządkować można przeregulowanie
odpowiedzi skokowej członu drugiego rzędu). Zapas fazy zaprojektowanego układu wynosi
, zaś zapas wzmocnienia
. Na rysunku a przedstawiono obraz linii pierwiastkowych odpowiadających sterowanemu obiektowi. Rysunek b dotyczy linii pierwiastkowych układu złożonego z obiektu oraz zaprojektowanego sterownika PID.

Obraz linii pierwiastkowych układu sterowania:

a) układ bez sterownika, b) układ ze sterownikiem PID

Zauważmy, iż skokowa odpowiedź układu zamkniętego jest nieco wolniejsza w stosunku do wymagań - wynika to z przybliżonego charakteru opisanej metody projektowania (na własności dynamiczne układu sterowania wpływają także zera oraz niedominujące bieguny operatorowej transmitancji tego układu). Przyspieszenie przejściowych procesów sterowania uzyskać można, przyjmując "nieco" mniejszą niż poprzednio wartość parametru
skali czasu (przy zachowaniu wartości współczynnika tłumienia
). Załóżmy przykładowo
, czemu odpowiadają parametry:
,
,
,
,
oraz
. Wyznaczone na tej podstawie skorygowane nastawy sterownika PID wynoszą:
,
oraz
. Odpowiedź skokowa układu sterowania charakteryzuje się czasem ustalania
oraz przeregulowaniem
. Zapas fazy tego układu wynosi
, zaś zapas wzmocnienia
.

Przykład 10 (sterownik pierwszego rzędu - wzory ogólne)

Obiekt o operatorowej transmitancji
sterowany jest w układzie z jednostkowym ujemnym sprzężeniem zwrotnym przy pomocy sterownika o transmitancji

,
.

Jakie warunki muszą spełniać parametry
,
oraz
tej transmitancji, aby równanie charakterystyczne układu zamkniętego posiadało parę pierwiastków zespolonych (
)?

Rozwiązanie

Niech
oraz
. Zakładając, iż
, po przekształceniach, otrzymujemy wzory

,

.

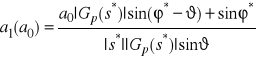
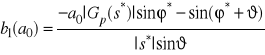
Uzyskane wyniki warto opatrzyć następującymi uwagami.

a) Pierwiastki (
) przyjmuje się na podstawie specyfikacji dotyczących stabilności układu zamkniętego oraz szybkości procesów sterowania. Wartość swobodnego parametru
określa się zwykle na podstawie wymaganej statycznej dokładności układu sterowania. Ponieważ zakłada się, iż
, zatem
, a stąd wynika, iż
.

b) Żądanie aby sterownik był stabilny prowadzi do warunku
. Rozważmy sytuację najczęściej występującą w praktyce:
, czemu odpowiada
. Uwzględniając warunek
, wyznaczamy maksymalną dopuszczalną wartość swobodnego parametru

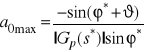
przy
.

Wartości tej odpowiada
, co prowadzi do sterownika PD o idealizowanej postaci transmitancji. Ze względu na powyższe ograniczenie wartości parametru
, omawiana metoda syntezy może okazać się niewystarczająca w przypadkach, gdy zadaniem sterownika jest przede wszystkim zwiększenie statycznej dokładności układu sterowania.

c) Początkowa wartość
sygnału sterującego obiektem przy jednostkowym pobudzeniu
oraz zerowych warunkach początkowych wynosi

.

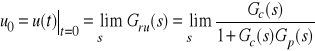
W przypadku sterowanego obiektu opisanego ściśle właściwą operatorową transmitancją
oraz przy przyjętej transmitancji
sterownika mamy
. Otrzymujemy zatem następujące oszacowanie

,

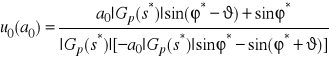
z którego wynika, iż zmieniając wartość parametru
możemy do pewnego stopnia kształtować postać sygnału sterującego obiektem.

d) Zapewniając charakterystycznemu równaniu zamkniętego układu sterowania pierwiastki określone przez parę (
), nie gwarantuje się, w ogólności, iż dynamiczne własności tego układu będą zdeterminowane owymi pierwiastkami. Sytuacja, w której para (
) nie określa dominujących biegunów operatorowej transmitancji zamkniętego układu sterowania, zwykle świadczy o zbyt wygórowanych wymaganiach co do szybkości sterowania, trudnych do spełnienia przy założonej prostej strukturze sterownika.

Przykład 11 (sterownik pierwszego rzędu)

Obiekt opisany operatorową transmitancją

.

sterowany jest przy pomocy sterownika o transmitancji
w układzie z jednostkowym ujemnym sprzężeniem zwrotnym. W przypadku, gdy w układzie tym nie stosuje się dynamicznej korekcji (to znaczy przy
) skokowa odpowiedź układu zamkniętego charakteryzuje się zerowym przeregulowaniem
oraz czasem ustalania
. Wyznacz takie wartości parametrów
,
oraz
sterownika przyspieszającego fazę (lead)

,
,
,

dla których kosztem dopuszczalnego niewielkiego przeregulowania (
) uzyskuje się znaczne zwiększenie szybkości odpowiedzi skokowej układu zamkniętego (
).

Rozwiązanie

Zakłada się, iż własności układu zamkniętego określone są parą (
) dominujących biegunów transmitancji tego układu:
, przy czym wartości parametrów
oraz
wynikają z wymagań dotyczących odpowiedzi skokowej:
oraz
. Biegun
ma zatem postać
. Z warunku
wynika, iż
oraz

. (1)

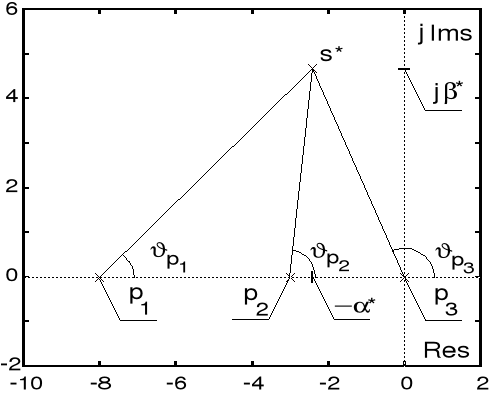
Zgodnie z poniższym rysunkiem, kąt
dany jest wzorem
, w którym
,
oraz
są kątowymi przyczynkami wnoszonymi przez bieguny
,
oraz
transmitancji sterowanego obiektu. Przy
zachodzi zatem
. Wynika stąd wartość przesunięcia fazowego, które przy
powinna zapewniać transmitancja sterownika:
.

Przyczynki fazowe Odpowiedzi skokowe

Na podstawie przyjętej postaci tej transmitancji wnioskujemy, iż

,

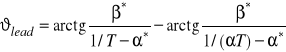
co pozwala na zapisanie następującej zależności

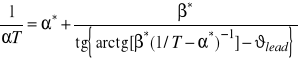
. (2)

Należy w tym miejscu podkreślić, iż opisywana procedura doboru parametrów sterownika lead opiera się na założeniu dodatniej wartości kąta
. W przypadku, gdy warunek
nie jest spełniony, niezbędna jest weryfikacja projektowych wymagań, wyrażonych w specyfikacji pary (
). Postawione zadanie syntezy sterownika lead nie posiada jednoznacznego rozwiązania: traktując
jako parametr swobodny, pozostałe parametry tego sterownika (to znaczy k oraz
) wyznaczyć można ze wzorów (1) oraz (2). W praktyce często proponuje się stosowanie kompensacyjnej reguły strojenia sterownika lead, według której parametr T dobiera się w ten sposób, aby jego wartość równała się największej stałej czasowej sterowanego obiektu. Inna wskazówka, pozwalająca na racjonalną parametryzację transmitancji sterownika lead, zaleca taki wybór T, aby iloczyn
- istotny ze względu na dokładność statyczną projektowanego układu - przyjmował możliwie dużą wartość (jak łatwo bowiem pokazać, zachodzi
). Zauważmy jednak, iż w przypadku gdy występują ograniczenia na wartość sygnału sterującego obiektem
, sformułować można regułę do pewnego stopnia przeciwstawną, nakazującą zmniejszanie wartości parametru
- początkowa wartość sygnału sterującego przy jednostkowym pobudzeniu
oraz zerowych warunkach początkowych równa się bowiem
.

Zakładając ścisłą kompensację dominującej stałej czasowej sterowanego obiektu, przyjmijmy
, co, zgodnie ze wzorami (1) oraz (2), prowadzi do następującej transmitancji sterownika lead:
,
. Zauważmy ponadto, iż w rozważanym przypadku zastosowanie sterownika typu lead zapewniło także istotne zwiększenie statycznej dokładności układu sterowania. Prędkościowe wzmocnienie układu przed i po korekcji wynosi bowiem odpowiednio
oraz
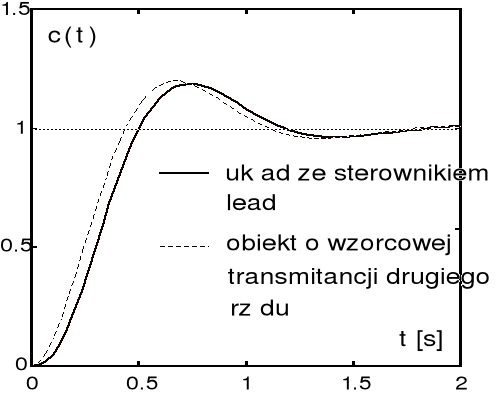
. Symulacja odpowiedzi skokowej tak zaprojektowanego układu sterowania (por. powyższy rysunek) pozwala na oszacowanie przeregulowania
oraz czasu ustalania
. Początkowa wartość sygnału sterującego obiektem wynosi
.

Przykład 12 (sterownik lead)

Obiekt o operatorowej transmitancji

jest sterowany w układzie z jednostkowym ujemnym sprzężeniem zwrotnym za pomocą sterownika przyspieszającego fazę lead, opisanego transmitancją
,
. Wyznacz parametry tego sterownika, przyjmując, iż zapas fazy zamkniętego układu sterowania powinien wynosić
, czas ustalania odpowiedzi skokowej
, zaś na początkową wartość
sygnału sterującego obiektem przy jednostkowej skokowej zmianie wielkości zadającej nałożone jest ograniczenie
.

Rozwiązanie

Zadanie rozwiążemy w oparciu o metodę opisaną w Przykładzie 11. W tym celu wyznaczamy parę żądanych pierwiastków zespolonych sprzężonych (
) równania charakterystycznego zamkniętego układu sterowania:
, przy czym
oraz
. Przyjmując
, otrzymujemy:
,
,
oraz
. Wartościom tym odpowiadają następujące parametry transmitancji sterowanego obiektu:
oraz
. Początkową wartość sygnału sterującego wyznaczamy ze wzoru

.

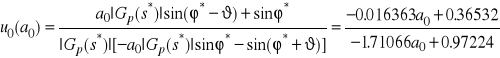
Przyjmując
, uzyskujemy
, a następnie obliczamy pozostałe parametry sterownika:
oraz
. Obraz linii pierwiastkowych układu sterowania bez tego sterownika oraz układu skorygowanego pokazano na rys. a,b. Zamknięty układ charakteryzuje się wskaźnikami:
,
oraz
.

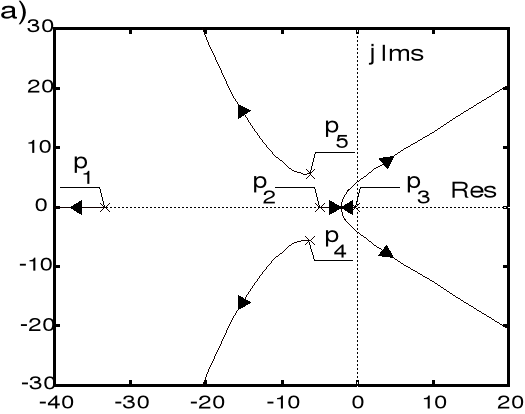
Obraz linii pierwiastkowych układu sterowania:

a) układ bez sterownika, b) układ ze sterownikiem lead

Zadania do samodzielnego rozwiązania

Zadanie 7

Obiekt o operatorowej transmitancji
jest sterowany w układzie z jednostkowym ujemnym sprzężeniem zwrotnym. Zaprojektuj taki sterownik PID o idealizowanej operatorowej transmitancji
, który zapewni temu układowi zapas fazy
, czas ustalania odpowiedzi skokowej
oraz współczynnik prędkościowego wzmocnienia
.

Odpowiedź

Posługując się metodą opisaną w Przykładzie 8, znajdujemy następujące parametry sterownika PID:
,
oraz
. Założono przy tym, iż para dominujących biegunów transmitancji zamkniętego układu sterowania ma wartość
. Unormowany czas ustalania
skokowej odpowiedzi wzorcowego członu drugiego rzędu dla współczynnika tłumienia
, wynikającego z żądanego zapasu fazy
, wynosi
. Symulacja tak zaprojektowanego układu powinna dać następujące wyniki:
,
oraz

Zadanie 8

Obiekt o operatorowej transmitancji
jest sterowany w układzie z jednostkowym ujemnym sprzężeniem zwrotnym za pomocą sterownika PI opisanego transmitancją
. Układowi temu stawia się następujące wymagania: zapas fazy
oraz czas ustalania odpowiedzi skokowej
. Wyznacz odpowiadające temu wartości parametrów
oraz
sterownika.

Odpowiedź

Sterownik PI, zapewniający żądaną jakość sterowania, posiada parametry:
oraz
. Zamknięty układ sterowania charakteryzuje się zapasem fazy
oraz odpowiedzią skokową o czasie ustalania
i przeregulowaniu
. Zadanie rozwiązano, przyjmując następujące oszacowanie pary dominujących biegunów transmitancji tego układu:
.

Zadanie 9

Dla obiektu opisanego operatorową transmitancją
należy zaprojektować sterownik PI, przy którym zamknięty układ sterowania z jednostkowym ujemnym sprzężeniem zwrotnym posiada odpowiedź skokową o przeregulowaniu
oraz czasie ustalania
.

Odpowiedź

Przy następującej transmitancji sterownika PI:
, skokowa odpowiedź zamkniętego układu sterowania charakteryzuje się wskaźnikami:
oraz
. Sterownik ten zaprojektowano dla następującej przykładowej pary dominujących biegunów transmitancji układu zamkniętego:
.

Zadanie 10

Obiekt o operatorowej transmitancji
jest sterowany za pomocą sterownika PD opisanego idealizowaną operatorową transmitancją
. Wyznacz parametry tej transmitancji, przy których skokowa odpowiedź układu zamkniętego charakteryzuje się przeregulowaniem
oraz czasem ustalania
. Rozwiąż zadanie dla realizowalnego sterownika PD:
,
,
.

Odpowiedź

Sterownik PD, będący przykładowym rozwiązaniem postawionego zadania, opisany jest parametrami:
oraz
. Skokowa odpowiedź zamkniętego układu sterowania charakteryzuje się przeregulowaniem
oraz czasem ustalania
. Rozważając realizowalną postać transmitancji sterownika PD, uzyskano przykładowe rozwiązanie
. Zamknięty układ z tym sterownikiem posiada odpowiedź skokową o wskaźnikach:
oraz
. Rozwiązanie to odpowiada parze
dominujących biegunów transmitancji zamkniętego układu sterowania.

Zadanie 11

Układ sterowania złożony jest z obiektu o transmitancji
oraz sterownika przyspieszającego fazę opisanego transmitancją
,
,
. Przyjmując, iż wpływ dominującej stałej czasowej sterowanego obiektu będzie ściśle kompensowany odpowiednim zerem transmitancji sterownika, dobierz parametry tej transmitancji, zapewniające zamkniętemu układowi skokową odpowiedź o przeregulowaniu
oraz czasie ustalania
. Oszacuj wartość prędkościowego wzmocnienia układu sterowania przed korekcją oraz po zastosowaniu zaprojektowanego sterownika.

Odpowiedź

Sterownikiem spełniającym postawione wymagania jest sterownik typu lead o parametrach:
,
oraz
. Odpowiedź skokowa zamkniętego układu sterowania charakteryzuje się przeregulowaniem
oraz czasem ustalania
. Współczynnik prędkościowego wzmocnienia układu przed korekcją wynosi
, zaś po korekcji
. Powyższe wyniki uzyskano, przyjmując
jako parę dominujących biegunów transmitancji zamkniętego układu sterowania oraz stosując oszacowanie
unormowanego czasu ustalania skokowej odpowiedzi wzorcowego członu drugiego rzędu o współczynniku tłumienia
, jednoznacznie określonym przez nominalną wartość przeregulowania
.

Zadanie 12

Obiekt dynamiczny opisany operatorową transmitancją
podlega sterowaniu w układzie z jednostkowym ujemnym sprzężeniem zwrotnym przy pomocy sterownika typu lead o transmitancji
,
,
. Wyznacz wartości parametrów
,
oraz
tej transmitancji tak, aby odpowiedź skokowa układu zamkniętego była dwukrotnie szybsza w stosunku do odpowiedzi skokowej układu zamkniętego bez korekcji (to znaczy dla
), przy zachowaniu zbliżonej wartości przeregulowania tych odpowiedzi. Należy założyć ścisłą kompensację dominującej stałej czasowej sterowanego obiektu przez odpowiednie zero transmitancji sterownika.

Odpowiedź

Skokową odpowiedź układu zamkniętego bez dynamicznej korekcji (
) opisują następujące wskaźniki: przeregulowanie
oraz czas ustalania
(wartości te uzyskano na drodze komputerowej symulacji). Przyjmując, iż skokowa odpowiedź układu zamkniętego ze sterownikiem lead powinna charakteryzować się przeregulowaniem
oraz czasem ustalania
, otrzymuje się następującą postać transmitancji tego sterownika
,
. Rozwiązanie to odpowiada przykładowej parze
dominujących biegunów operatorowej transmitancji projektowanego układu zamkniętego. Skokową odpowiedź układu z tak zaprojektowanym sterownikiem opisują wskaźniki:
oraz
.

Zadanie 13

Obiekt o operatorowej transmitancji
podlega sterowaniu przy wykorzystaniu sterownika o transmitancji
,
, w układzie z jednostkowym ujemnym sprzężeniem zwrotnym. Wyznacz wartości parametrów
,
oraz
sterownika, zakładając, iż liczby
wyznaczają parę dominujących biegunów transmitancji zamkniętego układu sterowania, zaś na początkową wartość
sygnału sterującego obiektem, przy jednostkowej skokowej zmianie wielkości zadającej oraz zerowych warunkach początkowych, nałożone jest ograniczenie
. Oszacuj wartość ustalonego błędu
odtwarzania takiej wielkości zadającej oraz wykreśl obraz linii pierwiastkowych uzyskanego układu sterowania.

Odpowiedź

Zadanie rozwiązano stosując metodę opisaną w Przykładzie 10. Uzyskano sterownik typu lead o następującej operatorowej transmitancji
. Ustalony błąd śledzenia jednostkowego skokowego sygnału równa się
.

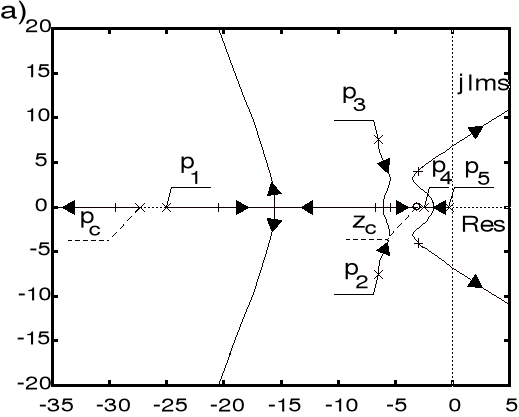
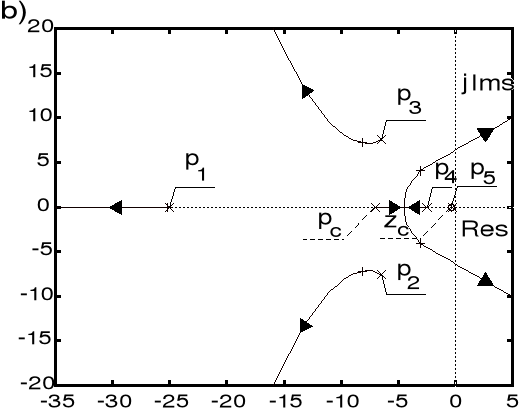
Rys. 6.36. Obraz linii pierwiastkowych układu sterowania:

a) metoda z Przykładu 10, b) metoda z Przykładu 11

: bieguny układu zamkniętego,
: biegun i zero sterownika lead

Zauważmy, iż zero
transmitancji sterownika
znacząco odbiega od wartości dominującego bieguna
transmitancji
sterowanego obiektu (rys. 6.36a). Zastosowana procedura projektowania nie wyklucza zatem rozwiązań odbiegających od prostej kompensacyjnej reguły wyznaczania parametru licznika transmitancji
. Porównajmy zatem uzyskane rozwiązanie z tym, które otrzymuje się w oparciu o taką regułę (por. Przykład 11):
. Ustalony błąd śledzenia jednostkowego sygnału skokowego równa się w tym przypadku
, zaś początkowa wartość sygnału sterującego obiektem wynosi
. Obraz linii pierwiastkowych rozważanego układu pokazano na rys. b.

Zadanie 14

Dany jest obiekt o operatorowej transmitancji
. Wyznacz parametry sterownika przyspieszającego fazę lead, który zastosowany w układzie z jednostkowym ujemnym sprzężeniem zwrotnym zapewnia zapas fazy
, czas ustalania odpowiedzi skokowej
oraz ustalony błąd tej odpowiedzi
. Czy proporcjonalny sterownik wystarcza do spełnienia postawionych wymagań?

Odpowiedź

Niech
,
, będzie poszukiwaną transmitancją sterownika lead.

Przyjmując parametr
, przy czym
i
(
), uzyskano przykładowe rozwiązanie:
. Zamknięty układ z takim sterownikiem charakteryzuje się zapasem fazy
oraz odpowiedzią skokową z czasem ustalania
oraz ustalonym błędem
. Sterownik proporcjonalny o wzmocnieniu
prowadzi do układu zamkniętego o żądanym zapasie fazy
. Skokową odpowiedź tego układu opisują wskaźniki:
oraz
.

25

---