POLITECHNIKA RZESZOWSKA
im. I. Łukasiewicza
Wydział Budowy Maszyn i Lotnictwa
Zakład Pojazdów Samochodowych
EKONOMIKA i ZARZĄDZANIE
w TRANSPORCIE SAMOCHODOWYM
PROJEKT NR 5.
Wykonał:
Arkadiusz Żywiec
V MDE
Konsultant:
dr inż. P. Pawlus
Temat: Opracować optymalny plan odnowy obiektu technicznego.
Dane:
N = 8
md = ma = mp = 2
p = 0,4
k |
F(k) |
1 |
0,1 |
2 |
0,3 |
3 |
0,5 |
4 |
0,7 |
5 |
0,9 |
6 |
1 |
7 |
1 |
8 |
1 |
Q = N⋅Δ - horyzont czasowy
ta = ma⋅Δ - czas trwania remontu bieżącego
td = md⋅Δ - czas trwania przeglądu (diagnozy)
tp = mp⋅Δ - czas trwania odnowy prewencyjnej
Δ - pewien odcinek czasu
p - prawdopodobieństwo wykrycia uszkodzenia podczas użytkowania
F(k) - prawdopodobieństwo uszkodzenia w czasie do „k” jednostek
f(k) = fk = F(k) - F(k-1) - prawdopodobieństwo uszkodzenia w konkretnym okresie czasie
Wyróżniamy cztery grupy:
E1 - element jest użytkowany
E2 - jest dokonywana diagnoza w wyniku której nie stwierdza się uszkodzenia
E3 - jest dokonywana diagnoza w wyniku której stwierdza się uszkodzenie
E4 - element jest odnawiany (wymieniany lub naprawiany)
p12 - prawdopodobieństwo przejścia ze stanu E1 do E2
p12(k) = 1- F(k)
p13 - prawdopodobieństwo przejścia ze stanu E1 do E3
p13(k) = (1-p)⋅ F(k)
![]()

k |
F(k) |
f(k) |
p12(k) |
p13(k) |
p⋅f(k) |
ω1(k) |
1 |
0,1 |
0,1 |
0,9 |
0,06 |
0,04 |
1 |
2 |
0,3 |
0,2 |
0,7 |
0,18 |
0,08 |
1,9 |
3 |
0,5 |
0,2 |
0,5 |
0,3 |
0,08 |
2,6 |
4 |
0,7 |
0,2 |
0,3 |
0,42 |
0,08 |
3,1 |
5 |
0,9 |
0,2 |
0,1 |
0,54 |
0,08 |
3,4 |
6 |
1 |
0,1 |
0 |
0,6 |
0,04 |
3,5 |
7 |
1 |
0 |
0 |
0,6 |
0 |
3,5 |
8 |
1 |
0 |
0 |
0,6 |
0 |
3,5 |
V1(m) - łączne efekty w okresie (Q - m, Q) jeżeli w momencie t1 = Q - m eksploatowany
element został poddany odnowie.
Równanie rekurencyjne wyprowadzone zgodnie z regułą optymalności programowania dynamicznego ma postać:
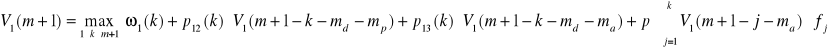
Zakłada się równocześnie, że V1(0) = 0
Jeżeli ko maksymalizuje prawą stronę równania, wówczas optymalna reguła określenia czasu przeglądu w momencie τ = Q-(m+1) jest równa G(τ) = ko
Dodatkowe założenia przewiduje, że przegląd jest dokonywany zawsze na końcu okresu stanowiącego horyzont czasowy analizowanego problemu.
![]()




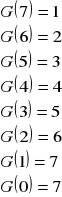
Planuje się dokonanie przeglądu po 7-miu latach, a następnie wraz z końcem horyzontu czasowego.
2
Wyszukiwarka