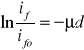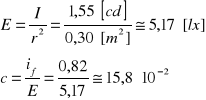Wydział: WIL	Imię i Nazwisko: Marcin Miś	Nr. Zespołu 5	Ocena Ostateczna
Grupa: Trzecia	Tytuł ćwiczenia: Zastosowanie fotoogniwa do pomiarów fotometrycznych	Nr. Ćwiczenia 22	Data Wykonania:

1. Wprowadzenie

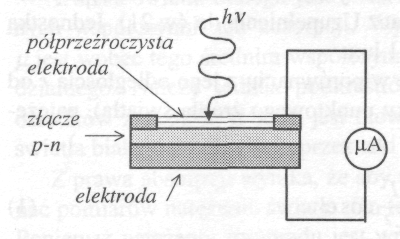
Fotoogniwo jest elementem, w którym wykorzystuje się zjawisko fotoelektryczne zaporowe (fotowoltaiczne). Zjawisko to polega na powstawaniu siły elektromotorycznej na styku dwu półprzewodników o różnym typie przewod­nictwa (n i p) lub półprzewodnika i metalu (jeśli praca wyjścia elektronów z metalu jest większa od pracy wyjścia elektronów z półprzewodnika) pod wpływem promieniowania elektromagnetycznego z zakresu częstości optycz­nych. Wartość powstającej siły elektromotorycznej zależy od rodzaju materiału użytego do konstrukcji fotoogniwa oraz natężenia oświetlenia jego powierzch­ni. Największe znaczenie praktyczne mają obecnie fotoogniwa ze złączem p-n. Typowe fotoogniwo ze złączem p-n składa się z elektrody bazowej wykonanej z metalu, na której znaj­duje się warstwa półprzewodnika. Warstwa ta pokryta jest półprzeźro­czystą dla światła cienką powłoką złota lub platyny stanowiącą drugą elektrodę. Między elektrodami oświetlonego fotoogniwa wytwarza się różnica potencjałów, która powoduje przepływ prądu w obwodzie zewnętrznym. Wartość tego prądu jest, w przypadku małego oporu w obwodzie zewnętrznym, w szerokim zakresie oświetleń liniową funk­cją natężenia oświetlenia E. Ta własność ułatwia zastosowanie fotoogniwa do pomiarów fotometrycznych takich, jak np. pomiary natężenia oświetlenia, światłości, strumienia świetlnego, współczynnika absorpcji światła, itp.

Efekt fotowoltaiczny związany jest z powstawaniem swobodnych nośników ładunku wewnątrz półprzewodnika, na który pada promieniowanie elektroma­gnetyczne, czyli ze zjawiskiem fotoelektrycznym. O ile w złączach p-n nie spolaryzowanych zewnętrznym napięciem elektrycznym zjawisko fotoelektryczne prowadzi do pojawienia się na złączu stałej różnicy potencjałów, to w przypadku wstępnego spolaryzowania złącza w kierunku zaporowym, zjawisko fotoelektryczne spowoduje zmianę oporu złącza, jak to ma miejsce w fotodiodach.

• Charakterystyka oświetleniowa fotoogniwa

Charakterystyka oświetleniowa przedstawia zależność natężenia fotoprądu i_f od natężenia oświetlenia E powierzchni fotoogniwa. Natężenie oświetlenia charakteryzuje powierzchniową gęstość strumienia promieniowania i definio­wane jest równaniem: E = dΦ/dS, gdzie dΦ jest strumieniem świetlnym pada­jącym na element powierzchni dS. Jednostką natężenia oświetlenia w układzie SI jest l lux.

Gdy rozmiary źródła światła są małe w porównaniu z jego odległością r od oświetlanej powierzchni, natęże­nie oświetlenia znajduje się z wzoru:

Wykorzystując charakterystykę oświetleniową można obliczyć czułość oświetleniową fotoogniwa:

i wyznaczyć nieznane oświetlenie dzieląc odpowiadająca mu wartość fotoprądu i_f przez c.

• Współczynnik absorpcji

Prawo absorpcji mówi, że jeżeli przez jednorodny, bezbarwny i przeźro­czysty ośrodek biegnie równoległa wiązka promieni świetlnych prostopadle do powierzchni ośrodka, to ulega ona wówczas osłabieniu zgodnie z równaniem:

J = J_oe^-μd

Wiązka światła białego jest mieszaniną fal o różnych długościach λ i róż­nych współczynnikach absorpcji. Występujący w tym wzorze współczynnik μ jest wobec tego średnim współczynnikiem absorpcji dla promieniowania wi­dzialnego. Należy jednak podkreślić, że dla przeźroczystych, bezbarwnych ośrodków zależność μ od λ jest niewielka, o czym świadczy fakt, że wiązka światła białego po przejściu przez taki ośrodek pozostaje nadal bezbarwna.

Z prawa absorpcji wynika, że aby wyznaczyć współczynnik μ. należy doko­nać pomiarów natężenia światła. Do tego celu można wykorzystać fotoogniwo. Ponieważ natężenie fotoprądu jest wprost proporcjonalne do / możemy napi­sać:

I_f = kJ = kJ_oe^-μd = i_foe^-μd

gdzie: k to współczynnik proporcjonalności, i_fo - natężenie fotoprądu zarejes­trowane przed przejściem światła przez ośrodek i_f natę­żenie fotoprądu zarejestrowane po przejściu światła przez ośrodek o grubości d. Stąd:

a po przekształceniu dostajemy:

lni_f = lni_fo - μd

gdzie i_f, i_fo są liczbami niemianowanymi.

Jak widać lni_f jest liniową funkcją grubości warstwy absorpcyjnej. Z tego równania wyznaczymy współczynnik absorpcji /zmierzać natężenie fotoprądu w funkcji grubości tej warstwy.

2. Tabele Pomiarowe

Tabela 1

Lp	r m	r^2 m^2	r^-2 m^-2	if μA
1	0,40	0,16	6,25	1,46
2	0,45	0,20	5,00	1,18
3	0,50	0,25	4,00	0,98
4	0,55	0,30	3,33	0,82
5	0,60	0,36	2,78	0,70
6	0,65	0,42	2,38	0,61
7	0,70	0,49	2,04	0,53
8	0,75	0,56	1,79	0,47
9	0,80	0,64	1,56	0,46
10	0,85	0,72	1,39	0,43
11	0,90	0,81	1,23	0,40
12	0,95	0,90	1,11	0,35
13	1,00	1,00	1,00	0,32

Tabela 2

Lp	d cm	if μA
1	0	8,25
2	1,05	6,25
3	2,10	5,20
4	3,15	4,25
5	4,20	3,55
6	5,25	3,00
7	6,30	2,60
8	7,35	2,15
9	8,40	1,80

Światło źródła = 1,55 [cd]

Ćwiczenie 1

Na podstawie Tabeli 1 rysuje wykres charakterystyki oświetleniowej fotoogniwa korzystając z metody regresji liniowej:

Wykres został wykonany przy pomocy programu udostępnionego w laboratorium który jednocześnie wyliczył prostą z regresji liniowej.

y=Ax + B gdzie A = 0.214 ± 0.003, a B = 0.111 ± 0.008

Następnie korzystając z wykresu obliczam czułość oświetleniową fotoogniwa. Jest ona dla badanego zakresu oświetleń stała.

Z zależności E = i_f/c obliczam oświetlenie panujące w laboratorium:

Ćwiczenie 2

Sporządzam wykres zależności fotoprądu od grubości płyt absorpcyjnych

otrzymałem wykres :

y = 8e^-0,175x

zgodnie z własnością logarytmu obliczam współczynnik absorpcji:

lnCe^-ax = lnC - ax

μ = -a [cm^-1]

Zatem szukany współczynnik to:

μ = 17,5 * 10^-2 [cm^-2]

3

---