PRZYKŁAD OBLICZANIA WIĄZARA PŁATWIOWO - KLESZCZOWEGO

1. Dach

Dane:

• Nachylenie połaci dachowej: α = 22°,

• Konstrukcja dachu: płatwiowo-kleszczowa, drewno sosnowe,

• Rozstaw krokwi: a = 1,00 m,

• Pokrycie: blacha trapezowa gr. 0,75 mm, wysokość 55 mm,

• Obciążenie śniegiem: strefa IV,

• Obciążenie wiatrem: strefa III,

• Położenie budynku: 350 m n.p.m.

1. Podkład pod pokrycie - łata

1. Zestawienie obciążeń

Przyjęto:

• rozstaw łat co 0,5 m,

• łaty o wymiarach 45 × 63 mm ⇒ A = 2,835⋅10^-3 m², ρ_sosny = 5,5 kN/m³.

• Obciążenia stałe

Tabela 1.1. Zestawienie obciążeń stałych

Obciążenie		Wartość charakterystyczna [kN/m]	Współczynnik obciążenia γf	Wartość obliczeniowa [kN/m]
Ciężar własny łaty 0,002835⋅5,5		0,016	1,1	0,018
Ciężar blachy trapezowej 0,091⋅0,5		0,046	1,2	0,055
RAZEM	0,062		0,073

• Obciążenie skupione (człowiek z narzędziami)

P_k = 1,0 kN, γ_f = 1,2 ⇒ P_d = 1,0⋅1,2 = 1,2 kN.

• Obciążenie zmienne

Obciążenie charakterystyczne śniegiem S_k na 1 m² powierzchni rzutu dla IV strefy (wg PN-80/B-02010):

;

gdzie:

Q_k = 0,003⋅H ≥ 0,9 kN/m², w tym: H - wysokość w m n.p.m.

Q_k = 0,003⋅350 = 1,05 kN/m².

C₁ = 0,8, C₂ =
,

C₁, C₂ - współczynniki kształtu dachu (wg Z1-1 ww. normy). Zgodnie z normą do obliczeń pojedynczych elementów przyjmuje się C₁ (patrz dopisek na dole tabeli Z1-1 ww. normy).

Obciążenie charakterystyczne wywołane działaniem wiatru (wg PN-77/B-02011) dla III strefy:

,

gdzie:

q_k = 250 + 0,5H ≥ 350 (H - wysokość w m n.p.m.) - charakterystyczne ciśnienie prędkości wiatru w III strefie obciążenia,

q_k = 250 + 0,5⋅350 = 425 Pa ⇒ q_k = 0,425 kN/m².

C_e - współczynnik ekspozycji. Przyjęto C_e = 0,8 (rodzaj terenu B - zabudowany przy wysokości istniejących budynków do 10 m lub zalesiony),

C - współczynnik aerodynamiczny dla dachu dwuspadowego (wg Z1-3 ww. normy) może przyjmować następujące wartości:

C =
= 0,015⋅22 - 0,2 = 0,13 (połać nawietrzna); lub
(wartość tą pomijamy, ponieważ pomniejsza ona ciężar dachu)

C = C_z = - 0,4 (połać zawietrzna).

β - współczynnik działania porywów wiatru. Dla budynków murowanych niepodatnych na dynamiczne działanie wiatru β = 1,8.

Zestawienie obciążeń zmiennych zestawiono w poniższej tabeli.

Tabela 1.2. Zestawienie obciążeń zmiennych

Obciążenie	Wartość charakterystyczna [kN/m]	Współczynnik obciążenia γf	Współczynnik jednoczesności obciążeń zmiennych ψo	Wartość obliczeniowa [kN/m]
Śnieg Sk⋅0,5 m = 1,05⋅0,80⋅0,5	0,42	1,4		0,588
Wiatr pk⋅0,5 m = 0,425⋅0,8⋅0,13⋅1,8⋅0,5	0,04	1,3	0,9	0,047

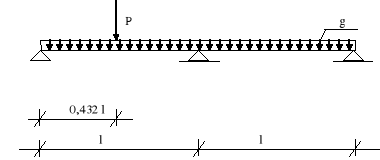
1. Schemat statyczny I - ciężar własny + człowiek

Przyjęto średni rozstaw między krokwiami l_{śr =}1,0 m.

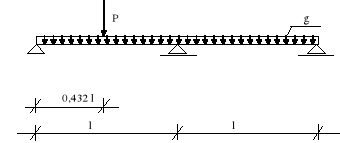
Składowe obciążenia charakterystycznego:

P_k⊥ = P_k⋅cosα = 0,927⋅P_k,

P_k|| = P_k⋅sinα = 0,375⋅P_k,

g_k⊥ = g_k⋅cosα = 0,927⋅g_k,

g_k|| = g_k⋅sinα = 0,375⋅g_k.

• Sprawdzenie stanu granicznego nośności (zginanie)

• wykres momentów zginających dla składowych prostopadłych obciążenia

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:

------------------------------------------------------------------

Grupa: Znaczenie: d: γf:

------------------------------------------------------------------

A -"Ciężar własny łaty" Stałe 1,10

B -"Obciążenie skupione" Zmienne 1 1,00 1,20

C -"Ciężar własny blachy trap." Stałe 1,20

------------------------------------------------------------------

MOMENTY:

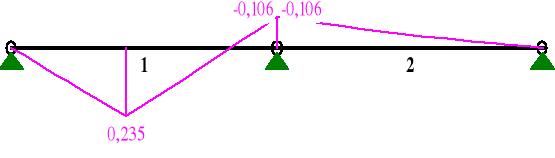
SIŁY PRZEKROJOWE: T.I rzędu

Obciążenia obl.: ABC

------------------------------------------------------------------

Pręt: x/L: x[m]: M[kNm]: Q[kN]: N[kN]:

------------------------------------------------------------------

1 0,00 0,000 0,000 0,560 0,000

0,43 0,432 0,235* -0,582 0,000

0,43 0,432 0,235* 0,530 0,000

1,00 1,000 -0,106 -0,621 0,000

2 0,00 0,000 -0,106 0,140 0,000

1,00 1,000 -0,000 0,072 0,000

------------------------------------------------------------------

* = Wartości ekstremalne

• wykres momentów zginających dla składowych równoległych obciążenia

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:

------------------------------------------------------------------

Grupa: Znaczenie: d: γf:

------------------------------------------------------------------

A -"Ciężar własny łaty" Stałe 1,10

B -"Obciążenie skupione" Zmienne 1 1,00 1,20

C -"Ciężar własny blachy trap." Stałe 1,20

------------------------------------------------------------------

MOMENTY:

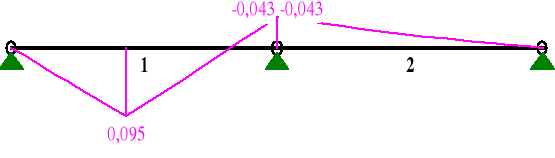
SIŁY PRZEKROJOWE: T.I rzędu

Obciążenia obl.: ABC

------------------------------------------------------------------

Pręt: x/L: x[m]: M[kNm]: Q[kN]: N[kN]:

------------------------------------------------------------------

1 0,00 0,000 0,000 0,226 0,000

0,43 0,432 0,095* -0,235 0,000

0,43 0,432 0,095* 0,215 0,000

1,00 1,000 -0,043 -0,251 0,000

2 0,00 0,000 -0,043 0,056 0,000

1,00 1,000 0,000 0,029 0,000

------------------------------------------------------------------

* = Wartości ekstremalne

• Sprawdzenie warunków:

,

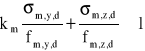
lub

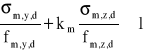
, gdzie:

σ_m,y,d i σ_m,z,d - są naprężeniami obliczeniowymi od zginania w stosunku do osi głównych,

f_m,y,d i f_m,z,d - są odpowiadającymi tym naprężeniom wytrzymałościami obliczeniowymi na zginanie,

k_m = 0,7 - dla przekrojów prostokątnych,

,
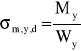
gdzie:

W_y i W_z - wskaźniki wytrzymałości.

,
.

.

.

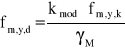
, gdzie:

f_m,y,k - wytrzymałość charakterystyczna na zginanie. Dla klasy drewna C30 f_m,y,k = 30 MPa,

γ_M = 1,3 - częściowy współczynnik bezpieczeństwa,

k_mod = 1,1 - współczynnik modyfikacyjny dla klas użytkowania i czasu trwania obciążenia (człowiek z narzędziami - obciążenie chwilowe) ,

.

,

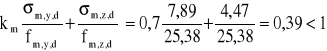
lub

.

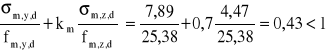
Warto zauważyć, że współczynnik k_m wystarczy stosować do „mniejszego” z ułamków.

W odniesieniu do powyższego schematu, warunek stanu granicznego nośności został spełniony.

• Sprawdzenie stanu granicznego użytkowalności

u_net.fin = L/150 = 1000/150 = 6,66 mm.

Wariant I (obliczenia dokładne)

Po wykonaniu obliczeń w programie RM-Win dla obciążeń charakterystycznych otrzymano następujące wartości ugięcia:

Wykresy ugięcia dla składowych prostopadłych obciążenia

• od obciążenia siłą skupioną (obciążenie krótkotrwałe)

PRZEMIESZCZENIA:

DEFORMACJE: T.I rzędu

Obciążenia char.: B

------------------------------------------------------------------

Pręt: Wa[m]: Wb[m]: FIa[deg]: FIb[deg]: f[m]: L/f:

------------------------------------------------------------------

1 -0,0000 0,0000 -0,234 0,138 0,0012 813,3

2 -0,0000 -0,0000 0,138 -0,069 0,0005 2156,1

------------------------------------------------------------------

u_inst1,y = 0,0012 m = 1,20 mm,

k_def = 0 (obciążenie krótkotrwałe),

u_fin1,y =
= 1,20 mm.

• od obciążenia ciężarem własnym (obciążenie stałe)

PRZEMIESZCZENIA:

DEFORMACJE: T.I rzędu

Obciążenia char.: AC

------------------------------------------------------------------

Pręt: Wa[m]: Wb[m]: FIa[deg]: FIb[deg]: f[m]: L/f:

------------------------------------------------------------------

1 -0,0000 -0,0000 -0,006 0,000 0,0000 35877,6

2 -0,0000 -0,0000 0,000 0,006 0,0000 35877,6

------------------------------------------------------------------

u_inst2,y = 0 mm,

k_def = 0,8 (klasa trwania obciążenia = stałe, klasa użytkowania = 2),

u_fin2,y =
= 0 mm.

Ugięcie sumaryczne:

u_fin,y = u_fin1,y + u_fin2,y = 1,20 + 0 = 1,20 mm,

Wykresy ugięcia dla składowych równoległych obciążenia

• od obciążenia siłą skupioną (obciążenie krótkotrwałe)

PRZEMIESZCZENIA:

DEFORMACJE: T.I rzędu

Obciążenia char.: B

------------------------------------------------------------------

Pręt: Wa[m]: Wb[m]: FIa[deg]: FIb[deg]: f[m]: L/f:

------------------------------------------------------------------

1 -0,0000 0,0000 -0,185 0,110 0,0010 1025,7

2 -0,0000 -0,0000 0,110 -0,055 0,0004 2719,3

------------------------------------------------------------------

u_inst1,z = 0,0010 m = 1,00 mm,

k_def = 0 (obciążenie krótkotrwałe),

u_fin1,z =
= 1,00 mm.

• od obciążenia ciężarem własnym (obciążenie stałe)

DEFORMACJE: T.I rzędu

Obciążenia char.: AC

------------------------------------------------------------------

Pręt: Wa[m]: Wb[m]: FIa[deg]: FIb[deg]: f[m]: L/f:

------------------------------------------------------------------

1 -0,0000 0,0000 -0,005 0,000 0,0000 46160,1

2 -0,0000 0,0000 -0,000 0,005 0,0000 46160,1

------------------------------------------------------------------

u_inst2,z = 0 mm,

k_def = 0,8 (klasa trwania obciążenia = stałe, klasa użytkowania = 2),

u_fin2,z =
= 0 mm.

Ugięcie sumaryczne:

u_fin,z = u_fin1,z + u_fin2,z = 1,00 + 0 = 1,00 mm,

Ugięcie całkowite

Stan graniczny użytkowalności został spełniony.

Wariant I (obliczenia przybliżone)

Ugięcia belek ciągłych, gdy stosunek rozpiętości największego przęsła do najmniejszego nie przekracza 1:0,8, przy jednakowym obciążeniu wszystkich przęseł lub, gdy stosunek największego obciążenia jednego przęsła do najmniejszego obciążenia innego nie przekracza 1:0,8, przy zachowaniu jednakowej rozpiętości przęseł, można obliczać w przybliżeniu (patrz pt. 5.3 normy PN-B-03150:2000), przyjmując stosunek największego ugięcia belki ciągłej do największego ugięcia belki jednoprzęsłowej swobodnie podpartej:

1. dla przęseł skrajnych:

0,65 - przy obciążeniu stałym,

0,90 - przy obciążeniu zmiennym,

2. dla przęseł środkowych:

0,25 - przy obciążeniu stałym,

0,75 - przy obciążeniu zmiennym.

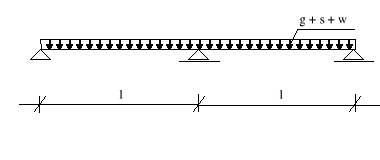
1. Schemat statyczny II - ciężar własny + śnieg + wiatr

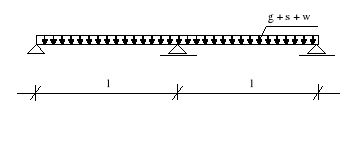
Składowe obciążenia charakterystycznego:

g_k⊥ = g_k⋅cosα = 0,927⋅g_k,

g_k|| = g_k⋅sinα = 0,375⋅g_k,

S_k⊥ = S_k⋅cos²α = 0,927²⋅S_k,

S_k|| = S_k⋅sinα⋅cosα = 0,375⋅0,927⋅S_k,

p_k⊥ = p_k⋅ ψ_o = P_k⋅0,9^*,

p_k|| = 0.

^* Uwzględniono współczynnik jednoczesności obciążeń ψ_o = 0,9 (wg PN-82/B-02000)

• Sprawdzenie stanu granicznego nośności (zginanie)

• wykres momentów zginających dla składowych prostopadłych obciążenia

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:

------------------------------------------------------------------

Grupa: Znaczenie: d: γf:

------------------------------------------------------------------

A -"Ciężar własny łaty" Stałe 1,10

B -"Śnieg" Zmienne 1 1,00 1,40

C -"Wiatr" Zmienne 1 1,00 1,30

D -"Cięzar własny blachy trap." Stałe 1,20

------------------------------------------------------------------

MOMENTY:

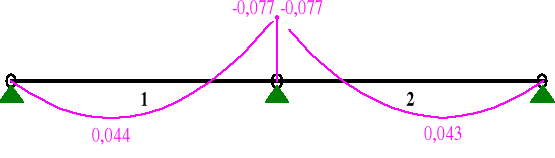
• wykres momentów zginających dla składowych równoległych obciążenia

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:

------------------------------------------------------------------

Grupa: Znaczenie: d: γf:

------------------------------------------------------------------

A -"Ciężar własny łaty" Stałe 1,10

B -"Śnieg" Zmienne 1 1,00 1,40

D -"Ciężar własny blachy trap." Stałe 1,20

------------------------------------------------------------------

MOMENTY:

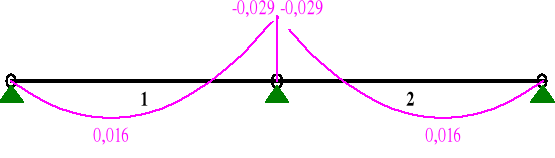
Wniosek:

Jak widać otrzymane wartości momentów zginających, zarówno w przypadku obciążeń działających prostopadle jak i równolegle do połaci dachowej są mniejsze od wartości otrzymanych w schemacie I (ciężar własny + człowiek). Wynika z tego, że ta kombinacja obciążeń jest mniej niebezpieczna dla sprawdzanego ustroju i dlatego nie ma potrzeby sprawdzania stanu granicznego nośności oraz stanu granicznego użytkowalności.

1. Wiązar płatwiowo - kleszczowy

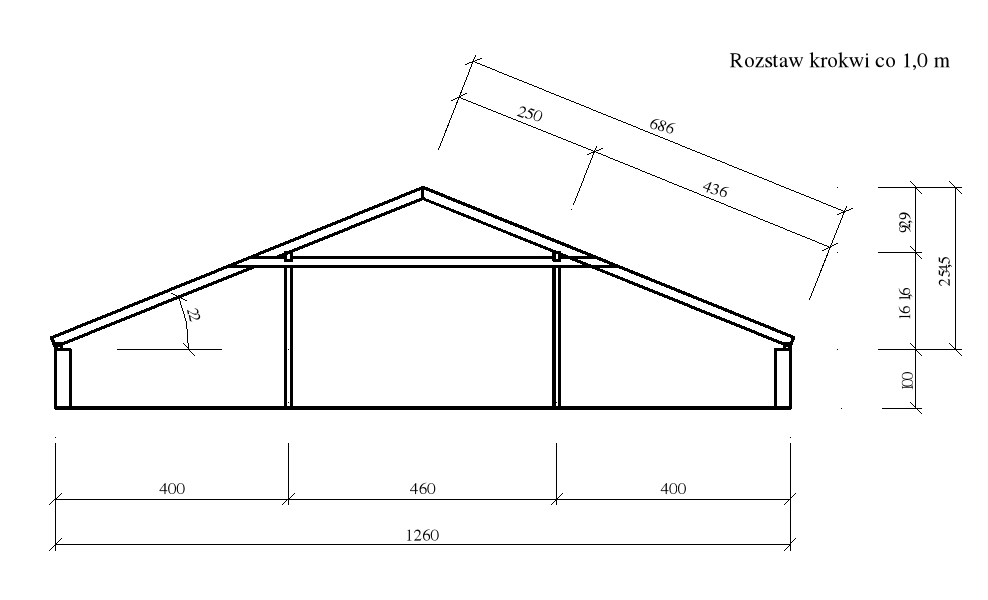
Przyjęto wstępnie:

krokwie 5,0 × 17,5 cm,

kleszcze 2 × 3,8 × 15 cm.

1. Zestawienie obciążeń

Zestawienie obciążeń połaci dachowych przedstawiono w tabeli 1.3. Składowe obciążenia połaci obliczono, korzystając z zależności:

g_k⊥ = g_k⋅cosα = 0,927⋅g_k,

g_k|| = g_k⋅sinα = 0,375⋅g_k,

S_k⊥ = S_k⋅cos²α = 0,927²⋅S_k,

S_k|| = S_k⋅sinα⋅cosα = 0,375⋅0,927⋅S_k,

p_k⊥ = p_k⋅ψ_o^*,

p_k|| = 0,

P_k⊥ = P_k⋅cosα = 0,927⋅P_k,

P_k|| = P_k⋅sinα = 0,375⋅P_k.

^* Uwzględniono współczynnik jednoczesności obciążeń ψ_o = 0,9 (wg PN-82/B-02000)

Tabela 1.3 Zestawienie obciążeń połaci dachowych więźby płatwiowo - kleszczowej

Obciążenie	Wartość charaktery-styczna [kN/m]	Współ-czynnik obcią-żenia γF	Wartość obliczeniowa [kN/m]	Składowe prostopadłe obciążenia		Składowe równoległe obciążenia
								wartość charaktery-styczna [kN/m]	wartość obliczeniowa [kN/m]	wartość charaktery-styczna [kN/m]	wartość obliczeniowa [kN/m]
Ciężar własny pokrycia z uwzględnieniem ciężaru krokwi ciężar łaty 0,016⋅2⋅1,0 m	0,032	1,1	0,035	0,030	0,032	0,012	0,013
ciężar własny blachy trapezowej 0,091⋅1,0 m	0,091	1,2	0,109	0,084	0,101	0,034	0,041
ciężar własny krokwi 0,05⋅0,175⋅5,5	0,048	1,1	0,053	0,044	0,049	0,018	0,020
RAZEM: 0,123+0,048	gk = 0,171		gd = 0,197	gk⊥ = 0,158	gd⊥ = 0,182	gk|| = 0,064	gd|| = 0,074
Śnieg połać lewa Sk = Qk⋅C2 = 1,05⋅0,987⋅1,0 m połać prawa Sk = Qk⋅C1 = 1,05⋅0,80⋅1,0 m	Sk = 1,036^* Sk = 0,840^*	1,4 1,4	Sd = 1,450^* Sd = 1,176^*	Sk⊥ = 0,890 Sk⊥ = 0,722	Sd⊥ = 1,246 Sd⊥ = 1,011	Sk|| = 0,360 Sk|| = 0,292	Sd|| = 0,504 Sd|| = 0,409
Wiatr połać nawietrzna pk1 = qk⋅Ce⋅C⋅β = = 0,425⋅0,8⋅(0,015⋅22-0,2) ⋅1,8 połać zawietrzna pk2 = qk⋅Ce⋅C⋅β = = 0,425⋅0,8⋅(-0,4) ⋅1,8	pk1 = +0,080 pk2 = -0,245	1,3 1,3	pd1 = +0,104 pd2 = -0,319	pk⊥1= +0,072^** pk⊥2= -0,221^**	pd⊥1= +0,094^** pd⊥2= -0,287^**	- -	- -
Ciężar własny kleszczy 2⋅0,038⋅0,15⋅5,5	gk2 = 0,063	1,1	gd2 = 0,069	-	-	-	-
Obciążenie skupione (człowiek obciążający kleszcze)	Pk = 1,00 [kN]	1,2	Pd = 1,20 [kN]	-	-	-	-

^* Wartość na 1 m² powierzchni rzutu dachu

^** Uwzględniono współczynnik jednoczesności obciążeń ψ_o = 0,9

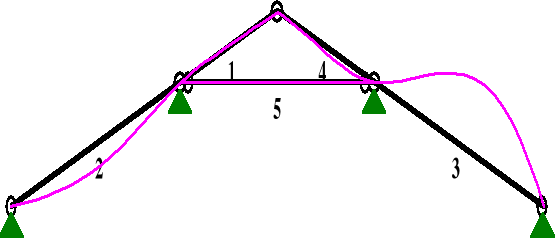
1. Schemat statyczny

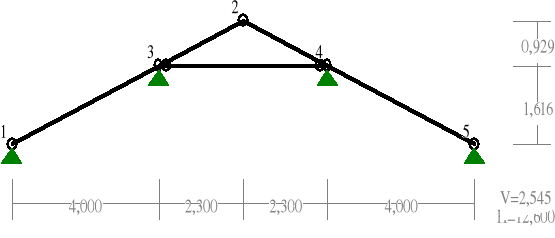
2. Wyznaczenie sił wewnętrznych

Obliczeń dokonano przy użyciu programu RM-Win. Otrzymane wyniki zamieszczono poniżej.

WĘZŁY:

------------------------------------------------------------------

Nr: X [m]: Y [m]: Nr: X [m]: Y [m]:

------------------------------------------------------------------

1 0,000 0,000 4 8,600 1,616

2 6,300 2,545 5 12,600 0,000

3 4,000 1,616

------------------------------------------------------------------

PODPORY: P o d a t n o ś c i

------------------------------------------------------------------

Węzeł: Rodzaj: Kąt: Dx(Do*): Dy: DFi:

[ m / k N ] [rad/kNm]

------------------------------------------------------------------

1 stała 0,0 0,000E+00 0,000E+00

3 przesuwna 0,0 0,000E+00*

4 przesuwna 0,0 0,000E+00*

5 przesuwna 0,0 0,000E+00*

------------------------------------------------------------------

OSIADANIA:

------------------------------------------------------------------

Węzeł: Kąt: Wx(Wo*)[m]: Wy[m]: FIo[grad]:

------------------------------------------------------------------

B r a k O s i a d a ń

------------------------------------------------------------------

PRĘTY:

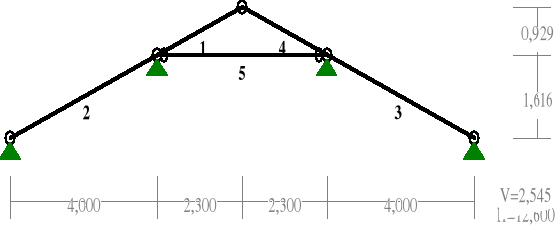
PRZEKROJE PRĘTÓW:

PRĘTY UKŁADU:

Typy prętów: 00 - sztyw.-sztyw.; 01 - sztyw.-przegub;

10 - przegub-sztyw.; 11 - przegub-przegub

22 - cięgno

------------------------------------------------------------------

Pręt: Typ: A: B: Lx[m]: Ly[m]: L[m]: Red.EJ: Przekrój:

------------------------------------------------------------------

1 01 3 2 2,300 0,929 2,481 1,000 2 Krokiew 175x50

2 00 1 3 4,000 1,616 4,314 1,000 2 Krokiew 175x50

3 00 4 5 4,000 -1,616 4,314 1,000 2 Krokiew 175x50

4 10 2 4 2,300 -0,929 2,481 1,000 2 Krokiew 175x50

5 11 3 4 4,600 0,000 4,600 1,000 1 Kleszcze 2 x 38x150

------------------------------------------------------------------

WIELKOŚCI PRZEKROJOWE:

------------------------------------------------------------------

Nr. A[cm2] Ix[cm4] Iy[cm4] Wg[cm3] Wd[cm3] h[cm] Materiał:

------------------------------------------------------------------

1 114,0 2344 2137 285 285 15,0 23 Drewno C30*

2 87,5 2233 182 255 255 17,5 23 Drewno C30*

------------------------------------------------------------------

* w przypadku używania w programie „starych” klas drewna należy zdefiniować własności drewna indywidualnie wg PN-B-03150:2000.

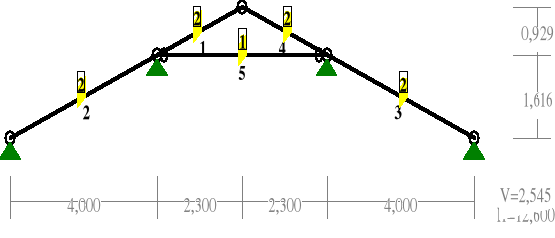
OBCIĄŻENIA:

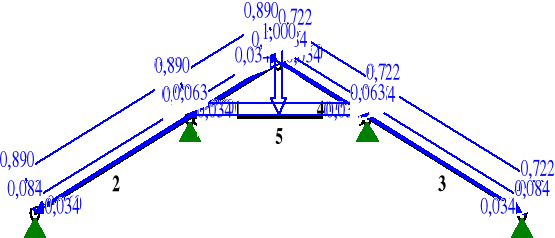
OBCIĄŻENIA: ([kN],[kNm],[kN/m])

------------------------------------------------------------------

Pręt: Rodzaj: Kąt: P1(Tg): P2(Td): a[m]: b[m]:

------------------------------------------------------------------

Grupa: A "C. wł. łata+krok, kleszcze" Stałe γf= 1,10

1 Liniowe 22,0 0,074 0,074 0,00 2,48

1 Liniowe -68,0 0,030 0,030 0,00 2,48

2 Liniowe 22,0 0,074 0,074 0,00 4,31

2 Liniowe -68,0 0,030 0,030 0,00 4,31

3 Liniowe -22,0 0,074 0,074 0,00 4,31

3 Liniowe 68,0 0,030 0,030 0,00 4,31

4 Liniowe -22,0 0,074 0,074 0,00 2,48

4 Liniowe 68,0 0,030 0,030 0,00 2,48

5 Liniowe 0,0 0,063 0,063 0,00 4,60

Grupa: B "Śnieg" Zmienne γf= 1,40

1 Liniowe 22,0 0,890 0,890 0,00 2,48

1 Liniowe -68,0 0,360 0,360 0,00 2,48

2 Liniowe 22,0 0,890 0,890 0,00 4,31

2 Liniowe -68,0 0,360 0,360 0,00 4,31

3 Liniowe -22,0 0,722 0,722 0,00 4,31

3 Liniowe 68,0 0,292 0,292 0,00 4,31

4 Liniowe -22,0 0,722 0,722 0,00 2,48

4 Liniowe 68,0 0,292 0,292 0,00 2,48

Grupa: C "Wiatr" Zmienne γf= 1,30

1 Liniowe 22,0 0,072 0,072 0,00 2,48

2 Liniowe 22,0 0,072 0,072 0,00 4,31

3 Liniowe -22,0 -0,221 -0,221 0,00 4,31

4 Liniowe -22,0 -0,221 -0,221 0,00 2,48

Grupa: D "Człowiek" Zmienne γf= 1,20

5 Skupione 0,0 1,000 2,30

Grupa: E "Ciężar własny blacha trap." Stałe γf= 1,20

1 Liniowe 22,0 0,084 0,084 0,00 2,48

1 Liniowe -68,0 0,034 0,034 0,00 2,48

2 Liniowe 22,0 0,084 0,084 0,00 4,31

2 Liniowe -68,0 0,034 0,034 0,00 4,31

3 Liniowe -22,0 0,084 0,084 0,00 4,31

3 Liniowe 68,0 0,034 0,034 0,00 4,31

4 Liniowe -22,0 0,084 0,084 0,00 2,48

4 Liniowe 68,0 0,034 0,034 0,00 2,48

------------------------------------------------------------------

==================================================================

W Y N I K I

Teoria I-go rzędu

==================================================================

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:

------------------------------------------------------------------

Grupa: Znaczenie: d: γf:

------------------------------------------------------------------

A -"C. wł. łata+krok, kleszcze" Stałe 1,10

B -"Śnieg" Zmienne 1 1,00 1,40

C -"Wiatr" Zmienne 1 1,00 1,30

D -"Człowiek" Zmienne 1 1,00 1,20

E -"Ciężar własny blacha trap." Stałe 1,20

------------------------------------------------------------------

MOMENTY:

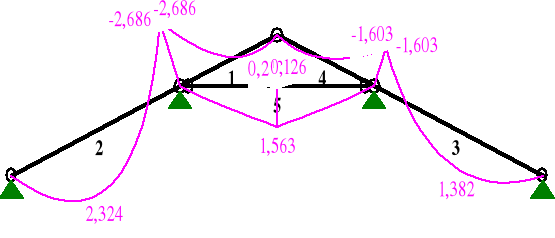
NORMALNE:

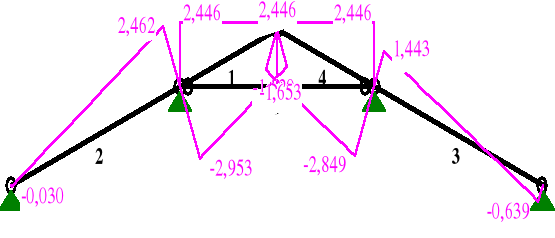
SIŁY PRZEKROJOWE: T.I rzędu

Obciążenia obl.: ABCDE

------------------------------------------------------------------

Pręt: x/L: x[m]: M[kNm]: Q[kN]: N[kN]:

------------------------------------------------------------------

1 0,00 0,000 -2,686 2,970 -2,953

0,79 1,957 0,213* -0,008 -1,822

0,79 1,948 0,213* 0,006 -1,828

1,00 2,481 0,000 -0,805 -1,520

2 0,00 0,000 0,000 2,660 -0,030

0,41 1,753 2,325* -0,007 0,982

1,00 4,314 -2,686 -3,905 2,462

3 0,00 0,000 -1,603 2,325 1,443

0,59 2,561 1,382* 0,005 0,207

1,00 4,314 0,000 -1,582 -0,639

4 0,00 0,000 0,000 0,477 -1,653

0,21 0,523 0,126* 0,003 -1,905

1,00 2,481 -1,603 -1,770 -2,849

5 0,00 0,000 0,000 0,759 2,446

0,50 2,300 1,563* 0,600 2,446

1,00 4,600 0,000 -0,759 2,446

------------------------------------------------------------------

* = Wartości ekstremalne

REAKCJE PODPOROWE:

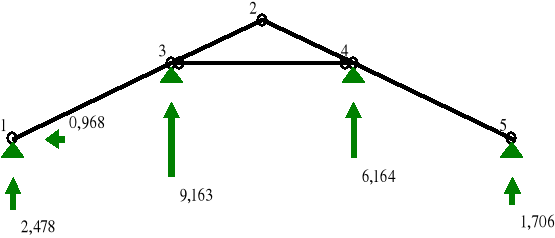
* ze względu na jednakowe wykonanie podpór w rzeczywistości, reakcję tę należy rozłożyć po połowie na obie podpory

REAKCJE PODPOROWE: T.I rzędu

Obciążenia obl.: ABCDE

------------------------------------------------------------------

Węzeł: H[kN]: V[kN]: Wypadkowa[kN]: M[kNm]:

------------------------------------------------------------------

1 -0,968 2,478 2,660

3 -0,000 9,163 9,163

4 -0,000 6,164 6,164

5 0,000 1,706 1,706

------------------------------------------------------------------

3. Wymiarowanie krokwi

• Sprawdzenie stanu granicznego nośności

Maksymalny moment zginający i odpowiadająca mu siła podłużna:

M₃ = 2,686 kNm,

N₃ = +2,462 kN (rozciąganie).

Warunku na zginanie i ściskanie (ponad płatwią) nie sprawdzano, jako bardziej korzystnego, ponieważ krokiew jest zabezpieczona przed wyboczeniem w obu płaszczyznach.

Przyjęto przekrój 50×175 mm,

A = b·h = 0,050·0,175 = 8,75⋅10^-3 m²,

W_y =
= 255,2·10^-6 m³.

• Sprawdzenie warunku na zginanie z osiową siłą rozciągającą (wzór 4.1.6.a z ww. normy)

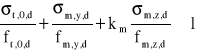
, gdzie:

k_mod = 0,9 - przyjęto (wg tabl. 3.2.5. PN-B-03150) dla drewna litego i klasy trwania obciążenia = krótkotrwałe (wiatr) oraz klasy użytkowania konstrukcji = 2 (wg p. 3.2.3. z ww. normy),

γ_M = 1,3 - częściowy współczynnik bezpieczeństwa,

=
,

=
,

,

,

.

.

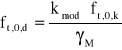
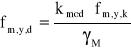
Warunek SGN został spełniony.

• Sprawdzenie stanu granicznego użytkowalności

u_net.fin = L/200 = 4360/200 = 21,8 mm.

Po wykonaniu obliczeń w programie RM-Win otrzymano następujące wartości ugięcia:

• od obciążenia ciężarem własnym

PRZEMIESZCZENIA:

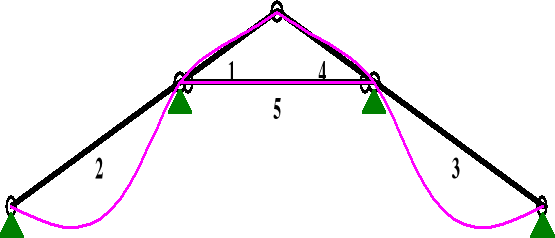
DEFORMACJE: T.I rzędu

Obciążenia char.: AE

------------------------------------------------------------------

Pręt: Wa[m]: Wb[m]: FIa[deg]: FIb[deg]: f[m]: L/f:

------------------------------------------------------------------

1 -0,0000 -0,0000 0,027 -0,004 0,0001 17183,8

2 -0,0000 -0,0000 -0,070 0,027 0,0015 2940,7

3 0,0000 0,0000 -0,027 0,070 0,0015 2940,7

4 -0,0000 0,0000 0,004 -0,027 0,0001 17183,8

5 -0,0000 -0,0000 0,000 0,000 0,0000 4,89E+37

------------------------------------------------------------------

u_inst1 = 1,5 mm,

k_def = 0,8 (klasa trwania obciążenia = stałe, klasa użytkowania = 2),

u_fin1 =
= 2,7 mm.

• od obciążenia śniegiem

PRZEMIESZCZENIA:

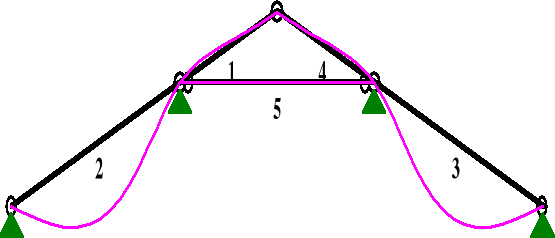
DEFORMACJE: T.I rzędu

Obciążenia char.: B

------------------------------------------------------------------

Pręt: Wa[m]: Wb[m]: FIa[deg]: FIb[deg]: f[m]: L/f:

------------------------------------------------------------------

1 -0,0000 -0,0001 0,154 -0,021 0,0008 3054,2

2 -0,0000 -0,0000 -0,395 0,154 0,0083 521,9

3 0,0000 0,0000 -0,124 0,320 0,0067 643,8

4 -0,0001 0,0000 0,018 -0,124 0,0007 3755,0

5 -0,0000 -0,0000 0,000 0,000 0,0000 6,11E+36

------------------------------------------------------------------

u_inst2 = 8,3 mm,

k_def = 0,25 (klasa trwania obciążenia = średniotrwałe, klasa użytkowania = 2),

u_fin2 =
= 10,4 mm.

• od obciążenia wiatrem

PRZEMIESZCZENIA:

DEFORMACJE: T.I rzędu

Obciążenia char.: C

------------------------------------------------------------------

Pręt: Wa[m]: Wb[m]: FIa[deg]: FIb[deg]: f[m]: L/f:

------------------------------------------------------------------

1 -0,0000 -0,0000 0,012 -0,002 0,0001 37870,1

2 -0,0000 -0,0000 -0,032 0,012 0,0007 6445,2

3 0,0000 0,0000 0,039 -0,098 0,0021 2092,4

4 0,0000 0,0000 -0,004 0,039 0,0002 12489,7

5 -0,0000 0,0000 0,000 0,000 0,0000 2,45E+37

------------------------------------------------------------------

u_inst3 = 0,7 mm,

k_def = 0 (klasa trwania obciążenia = krótkotrwałe, klasa użytkowania = 2),

u_fin2 =
= 0,7 mm.

Ugięcie całkowite:

u_fin = u_fin1 + u_fin2 + u_fin3 = 2,7 + 10,4 + 0,7 = 13,8 mm,

u_fin = 13,8 mm < u_net.fin = 21,8 mm.

Stan graniczny użytkowalności został spełniony. Biorąc pod uwagę „wykorzystanie” przekroju krokwi (0,53 < 1 i 13,8 mm < 21,8 mm), ze względów ekonomicznych wymiary krokwi należałoby zmniejszyć.

1. Wymiarowanie kleszczy

• Sprawdzenie stanu granicznego nośności

Moment zginający i siła podłużna:

M = 1,563 kNm

N = N_3-4·n = 2,446·4 = 9,784 kN, gdzie:

n - liczba wiązarów przypadająca na jedne kleszcze (kleszcze „zbierają” obciążenie również z wiązarów pustych),

Przyjęto przekrój 2×38×150 mm,

A = 2·b·h = 2·0,038·0,150 = 11,4⋅10^-3 m²,

.

• Sprawdzenie warunku na zginanie z osiową siłą rozciągającą (wzór 4.1.6.a z ww. normy)

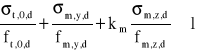
, gdzie:

k_mod = 0,9 - przyjęto (wg tabl. 3.2.5. PN-B-03150) dla drewna litego i klasy trwania obciążenia = krótkotrwałe (wiatr) oraz klasy użytkowania konstrukcji = 2 (wg p. 3.2.3. z ww. normy),

γ_M = 1,3 - częściowy współczynnik bezpieczeństwa,

=
,

=
,

,

,

.

.

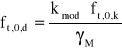
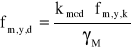
Warunek SGN został spełniony.

• Sprawdzenie stanu granicznego użytkowalności

u_net.fin = L/200 = 4600/200 = 23,0 mm.

Po wykonaniu obliczeń w programie RM-Win otrzymano następujące wartości ugięcia:

• od obciążenia ciężarem własnym

PRZEMIESZCZENIA:

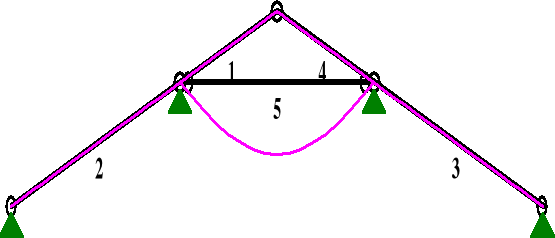
DEFORMACJE: T.I rzędu

Obciążenia char.: A

------------------------------------------------------------------

Pręt: Wa[m]: Wb[m]: FIa[deg]: FIb[deg]: f[m]: L/f:

------------------------------------------------------------------

1 -0,0000 -0,0000 -0,000 -0,000 0,0000 1,02E+18

2 0,0000 -0,0000 0,000 -0,000 0,0000 5,85E+17

3 0,0000 0,0000 0,000 -0,000 0,0000 2,53E+15

4 -0,0000 0,0000 -0,000 0,000 0,0000 2,54E+15

5 -0,0000 -0,0000 -0,057 0,057 0,0014 3212,4

------------------------------------------------------------------

u_inst1 = 1,4 mm,

k_def = 0,8 (klasa trwania obciążenia = stałe, klasa użytkowania = 2),

u_fin1 =
= 2,52 mm.

• od obciążenia siłą skupioną (człowiek)

PRZEMIESZCZENIA:

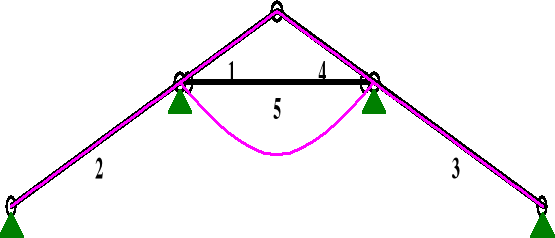
DEFORMACJE: T.I rzędu

Obciążenia char.: D

------------------------------------------------------------------

Pręt: Wa[m]: Wb[m]: FIa[deg]: FIb[deg]: f[m]: L/f:

------------------------------------------------------------------

1 -0,0000 -0,0000 -0,000 0,000 0,0000 1,15E+27

2 0,0000 -0,0000 -0,000 -0,000 0,0000 6,59E+26

3 -0,0000 0,0000 0,000 0,000 0,0000 6,59E+26

4 -0,0000 -0,0000 -0,000 0,000 0,0000 1,15E+27

5 -0,0000 -0,0000 -0,295 0,295 0,0079 581,9

------------------------------------------------------------------

u_inst2 = 7,9 mm,

k_def = 0 (klasa trwania obciążenia = krótkotrwałe, klasa użytkowania = 2),

u_fin2 =
= 7,9 mm.

Ugięcie całkowite:

u_fin = u_fin1 + u_fin2 = 2,52 + 7,90 = 10,42 mm,

u_fin = 10,42 mm < u_net.fin = 23,0 mm.

Stan graniczny użytkowalności został spełniony.

1. Wymiarowanie płatwi

Przyjęto przekrój 120x150 mm

A = b·h = 120·150 = 18000 mm²,

W_y = bh²/6 = 120·150²/6 = 450,0·10³ mm³.

W_z = hb²/6 = 150·120²/6 = 360,0·10³ mm³.

Tabela 1.3 Zestawienie obciążeń na płatew

Obciążenie	Wartość charaktery-styczna [kN/m]	Współ-czynnik obcią-żenia γF	Wartość obliczeniowa [kN/m]	Składowa pionowa obciążenia (z) na długości krokwi		Składowa pozioma obciążenia (y) na długości krokwi
								wartość charaktery-styczna [kN/m]	wartość obliczeniowa [kN/m]	wartość charaktery-styczna [kN/m]	wartość obliczeniowa [kN/m]
Ciężar własny pokrycia z uwzględnieniem ciężaru krokwi blacha trapezowa 0,091⋅1,0 m łaty (0,016⋅2)⋅1,0 m ciężar własny krokwi 0,05⋅0,175⋅5,5·1,0 m RAZEM: Ciężar własny płatwi 0,12⋅0,15⋅5,5·1,0 m	0,091 0,032 0,048 gk = 0,171 gkp = 0,099	1,2 1,1 1,1 1,1	0,109 0,035 0,053 gd = 0,197 gdp = 0,109	0,091 0,032 0,048 gkz = 0,171 gkpz = 0,099	0,109 0,035 0,053 gdz = 0,197 gdpz = 0,109	- - - gky = 0 gkpy = 0	- - - gdy = 0 gdpy = 0
Śnieg Sk = Qk⋅C = 1,05⋅0,987⋅1,0 m	Sk = 1,036^*	1,4	Sd = 1,451^*	Skz =Sk cosα= = 0,961	Sdz =Sd cosα= = 1,345	Sky = 0	Sdy = 0
Wiatr połać nawietrzna pk = qk⋅Ce⋅C⋅β = = 0,425⋅0,8⋅(0,015⋅22-0,2) ⋅1,8·1,0 m	pk = +0,080	1,3	pd = +0,104	pkz = pk cosα= = 0,067^**	pdz = pd cosα= = 0,087^**	pky = pk sinα= = 0,027^** -	pdy = pd sinα= = 0,035^** -

^* Wartość na 1 m² powierzchni rzutu dachu

^** Uwzględniono współczynnik jednoczesności obciążeń ψ_o = 0,9

Na płatew działa obciążenie z pasma szerokości 2,5 + 0,5·4,36 (odcinek górny + połowa dolnego odcinka krokwi).

• składowa pionowa obciążenia

q_kz = (g_kz + S_kz + p_kz)(2,5 + 0,5·4,36) + g_kpz = (0,171 + 0,961 + 0,067)(2,5 + 0,5·4,36) + 0,099 = 5,709 kN/m,

q_dz = (g_dz + S_dz + p_dz)(2,5 + 0,5·4,36) + g_kpz = (0,197 + 1,345 + 0,087)(2,5 + 0,5·4,36) + 0,109 = 7,733 kN/m,

• składowa pozioma obciążenia

q_ky = p_ky(2,5 + 0.5·4.36) = 0,027(2,5 + 0.5·4.36) = 0,126 kN/m,

q_dy = p_dy(2,5 + 0.5·4.36) = 0,035(2,5 + 0.5·4.36) = 0,164 kN/m.

• Sprawdzenie stanu granicznego nośności

Wyznaczenie sił wewnętrznych

Obliczeń dokonano przy użyciu programu RM-Win. Otrzymane wyniki zamieszczono poniżej.

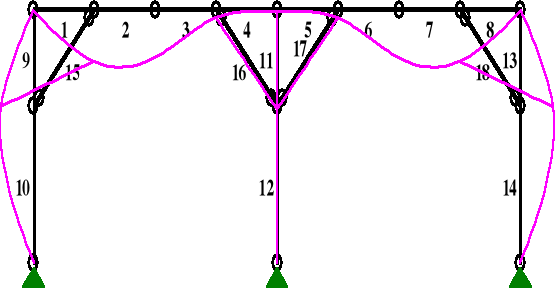
Płaszczyzna pionowa - rama o schemacie statycznym na rysunku poniżej

PRZEKROJE PRĘTÓW:

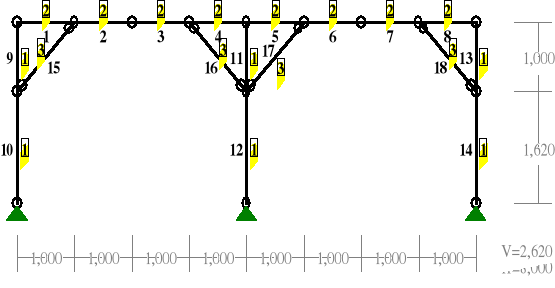
PRĘTY UKŁADU:

------------------------------------------------------------------

Pręt: Typ: A: B: Lx[m]: Ly[m]: L[m]: Red.EJ: Przekrój:

------------------------------------------------------------------

1 10 1 2 1,000 0,000 1,000 1,000 2 150x120C30

2 00 2 3 1,000 0,000 1,000 1,000 2 150x120C30

3 00 3 4 1,000 0,000 1,000 1,000 2 150x120C30

4 01 4 5 1,000 0,000 1,000 1,000 2 150x120C30

5 10 5 6 1,000 0,000 1,000 1,000 2 150x120C30

6 00 6 7 1,000 0,000 1,000 1,000 2 150x120C30

7 00 7 8 1,000 0,000 1,000 1,000 2 150x120C30

8 01 8 9 1,000 0,000 1,000 1,000 2 150x120C30

9 10 1 10 0,000 -1,000 1,000 1,000 1 100x100C30

10 01 10 11 0,000 -1,620 1,620 1,000 1 100x100C30

11 10 5 12 0,000 -1,000 1,000 1,000 1 100x100C30

12 01 12 13 0,000 -1,620 1,620 1,000 1 100x100C30

13 10 9 14 0,000 -1,000 1,000 1,000 1 100x100C30

14 01 14 15 0,000 -1,620 1,620 1,000 1 100x100C30

15 11 10 2 1,000 1,000 1,414 1,000 3 75x75C30

16 11 4 12 1,000 -1,000 1,414 1,000 3 75x75C30

17 11 6 12 -1,000 -1,000 1,414 1,000 3 75x75C30

18 11 8 14 1,000 -1,000 1,414 1,000 3 75x75C30

------------------------------------------------------------------

OBCIĄŻENIA:

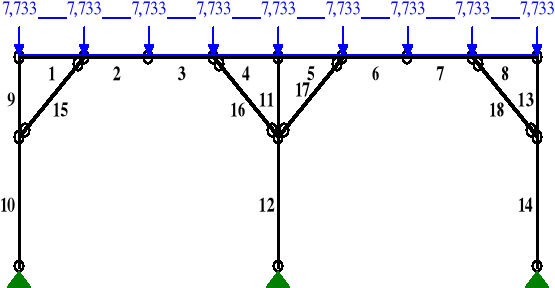
MOMENTY:

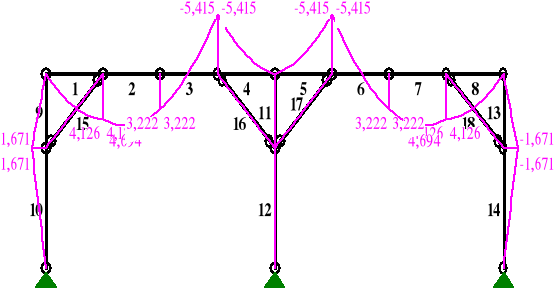
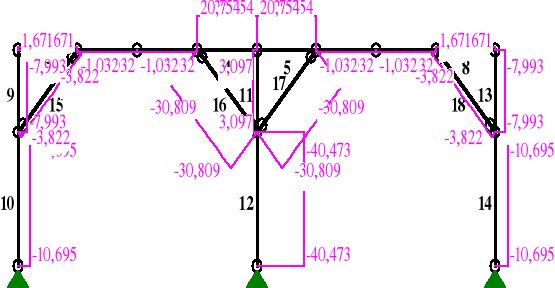
NORMALNE:

Płaszczyzna pozioma - belka jednoprzęsłowa o rozpietości l_y = 4,0 m (w osiach słupów)

PRZEKROJE PRĘTÓW:

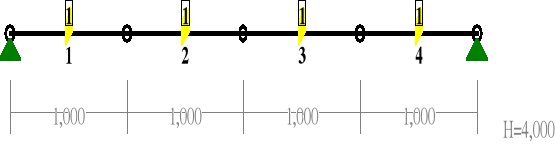
PRĘTY UKŁADU:

------------------------------------------------------------------

Pręt: Typ: A: B: Lx[m]: Ly[m]: L[m]: Red.EJ: Przekrój:

------------------------------------------------------------------

1 00 1 2 1,000 0,000 1,000 1,000 1 120x150C30

2 00 2 3 1,000 0,000 1,000 1,000 1 120x150C30

3 00 3 4 1,000 0,000 1,000 1,000 1 120x150C30

4 00 4 5 1,000 0,000 1,000 1,000 1 120x150C30

OBCIĄŻENIA:

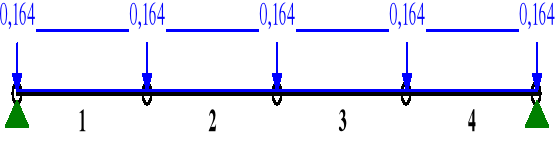
MOMENTY:

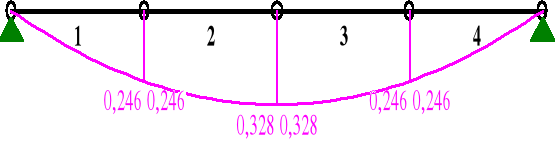
najbardziej wytężony jest przekrój 3-4, w którym:

M_y = 5,415 kNm

N = 20,754 kNm

M_z = 0,246 kNm

k_mod = 0,9 - przyjęto (wg tabl. 3.2.5. PN-B-03150) dla drewna litego i klasy trwania obciążenia = krótkotrwałe (wiatr) oraz klasy użytkowania konstrukcji = 2 (wg p. 3.2.3. z ww. normy)

γ_M = 1,3 - częściowy współczynnik bezpieczeństwa

f_t,0,d = f_t,0,k·k_mod/γ_M = 18·0,9/1,3 = 12,46 MPa,

f_m,y,d = f_m,z,d = f_m,k·k_mod/γ_M = 30·0,9/1,3 = 20,77 MPa,

σ_t,0,d = N/A = 20,754·10³/18000 = 1,15 MPa,

σ_m,y,d = M_y/W_y = 5,415·10⁶/(450·10³) = 12,03 MPa,

σ_m,z,d = M_z/W_z = 0,246·10⁶/(360·10³) = 0,68 MPa

Zginanie z osiową siłą rozciągającą (wzory 4.1.6.a i 4.1.6.b z ww. normy)

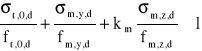
lub

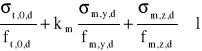
gdzie k_m = 0,7 dla przekrojów prostokątnych

Współczynnik k_m zmniejsza zawsze wartość mniejszego z dwóch ilorazów σ_myd/f_myd lub σ_mzd/f_mzd.

Warunek SGN został spełniony.

• Sprawdzenie stanu granicznego użytkowalności

I_y = bh³/12 = 120·150³/12 = 3375·10⁴ mm⁴,

I_z = b³h/12 = 120³·150/12 = 2160·10⁴ mm⁴,

E_0,mean = 12000 MPa (tabl. Z-2.2.3-1 z ww. normy).

Ugięcie od obciążenia ciężarem własnym i pokrycia:

k_def = 0,8 (klasa trwania obciążenia = stałe, klasa użytkowania = 2)

q_k1z = g_kz·(2,5 + 0,5·4,36) + g_kpz = 0,171·(2,5 + 0,5·4,36) +0,099 = 0,898 kN/m

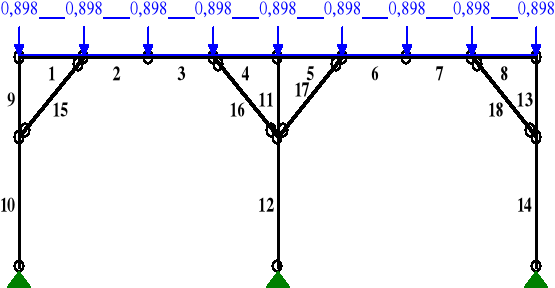
PRZEMIESZCZENIA:

odczytano z programu RM-Win:

u_inst,1,z = 1,2 mm

u_fin,1,z = u_inst,1,z (1 + k_def) = 1,2·(1 + 0,8) = 2,2 mm

Ugięcie od obciążenia śniegiem:

k_def = 0,25 (klasa trwania obciążenia = średniotrwałe, klasa użytkowania = 2)

q_k2z = S_kz·(2,5 + 0,5·4,36) = 0,961·(2,5 + 0,5·4,36) = 4,497 kN/m

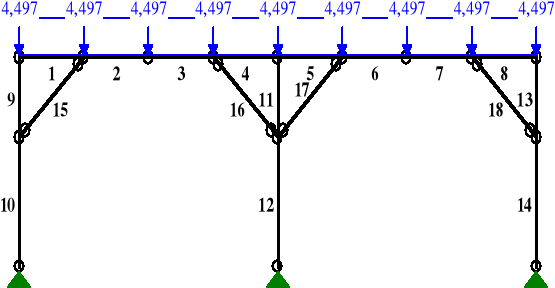
odczytano z programu RM-Win:

u_inst,2,z = 6,0 mm

u_fin,2,z = u_inst,2,z (1 + k_def) = 6,0 (1 + 0,25) = 7,5 mm

Ugięcie od obciążenia pionowego wiatrem:

k_def = 0 (klasa trwania obciążenia = krótkotrwałe, klasa użytkowania = 2)

q_k3z = p_kV·(2,5 + 0,5·4,36) = 0,067·(2,5 + 0,5·4,36) = 0,314 kN/m

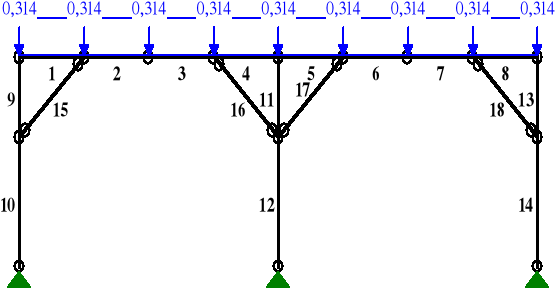
odczytano z programu RM-Win:

u_inst,3,z = 0,4 mm

u_fin,3,z = u_inst,3,z (1 + k_def) =0,4 (1 + 0) = 0,4 mm

Ugięcie od obciążenia poziomego wiatrem:

k_def = 0 (klasa trwania obciążenia = krótkotrwałe, klasa użytkowania = 2)

q_ky = p_kH·(2,5 + 0,5·4,36) = 0,027·(2,5 + 0,5·4,36) = 0,126 kN/m

l_z = 4,0 m, h = 0,14 m; l_y/h = 4,0/0,14 = 28,6 > 20

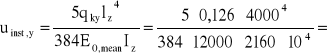
1,6 mm

u_fin,y = u_inst,y (1 + k_def) =1,6 (1 + 0) = 1,6 mm

Ugięcia finalne:

u_inst,z = u_inst,1,z + u_inst,2,z + u_inst,3,z = 1,2 + 6,0 + 0,4 = 7,6 mm

u_inst,y = 1,6 mm

mm

u_fin,z = u_fin,1,z + u_fin,2,z + u_fin,3,z = 2,2 + 7,5+ 0,4 = 10,1 mm

u_fin,y = 1,6 mm

mm

u_fin = 10,5 mm < u_net,fin = l/200 = 4000/200 = 20 mm

Wartości graniczne u_net,fin z tabl. 5.2.3. z ww. normy

Obliczone ugięcie jest mniejsze od ugięcia dopuszczalnego. Warunek SGU został spełniony.

1. Wymiarowanie słupa

Słup obliczono jako ściskany osiowo siłą P = 40,473 kN (z programu RM-Win, patrz wykres sił osiowych w p. 1.2.6)

Przyjęto przekrój słupa 100x100 mm

A_d = 100·100 = 10000 mm²

I_y = I_z = a⁴/12 = 100⁴/12 = 833·10⁴ mm⁴

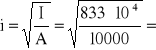
28,9 mm,

l_y = 2620 mm,

l_z = 2620 -1000 = 1620 mm,

λ_y = l_y/i_y = 2620/28,9 = 90,6 - smukłość względem osi y

σ_c,crit,y = π²·E_0,05/λ²_y (wzór 4.2.1.g z ww. normy)

σ_c,crit,y = π²·8000/90,6² = 9,62 MPa,

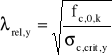
(wzór 4.2.1.c z ww. normy)

,

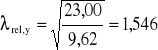
(wzór 4.2.1.e z ww. normy)

β_c - współczynnik dotyczący prostoliniowości elementów (dla drewna litego β_c = 0,2)

k_y = 0,5[1 + 0,2(1,546 - 0,5) + 1,546²] = 1,800

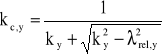
(wzór 4.2.1.a z ww. normy)

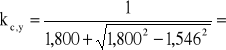
0,367

σ_c,0,d = P/A_d = 40,473·10³/10⁴ = 4,05 MPa

Stan graniczny nośności słupów osiowo ściskanych należy sprawdzać według warunku 4.2.1.j z PN-B-03150:2000:

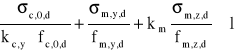
f_c,0,d = f_c,0,k·k_mod/γ_M = 23·0,9/1,3 = 15,92 MPa

Warunek SGN został spełniony.

Sprawdzenie docisku słupa do podwaliny

Powierzchnia docisku do podwaliny:

A_d = 100·100 = 10000 mm²

k_mod = 0,9 - przyjęto (wg tabl. 3.2.5. PN-B-03150) dla drewna litego i klasy trwania obciążenia = krótkotrwałe (wiatr) oraz klasy użytkowania konstrukcji = 2 (wg p. 3.2.3. z ww. normy)

γ_M = 1,3 - częściowy współczynnik bezpieczeństwa

f_c,90,d = f_c,90,k·k_mod/γ_M = 5,7·0,9/1,3 = 3,95 MPa,

σ_c,90,d = P/A_d = 40,473·10³/10000 = 4,05 MPa,

(wzór 4.1.4.a z ww. normy)

k_c,90 - współczynnik, który uwzględnia możliwość zwiększenia wytrzymałości kiedy długość obciążonego odcinka, wynikająca z rozkładu siły, oznaczona jako l na rys. 4.1.4.1. w ww. normie jest mała

(z tabl.4.1.4 z ww. normy)

dla a ≥ 100 mm, l₁ =.150 mm, l = 100 mm

5,09 MPa

Warunek SGN został spełniony.

2. Wymiarowanie mieczy

Przyjęto miecze usytuowane ukośnie pod kątem α = 45º między płatwią a słupem, o przekroju 75x75 mm i długości
m.

Miecz obliczono jako ściskany osiowo siłą S = 30,809 kN (z programu RM-Win, patrz wykres sił osiowych w p. 1.2.6)

Przekrój mieczy 75x75 mm

A_d = 75·75 = 5625 mm²

I_y = I_z = a⁴/12 = 75⁴/12 = 264·10⁴ mm⁴

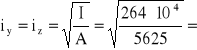
21,7 mm,

l_y = l_z = 1414 mm,

λ_y = l_y/i_y = 1414/21,7 = 65,2 - smukłość względem osi y

σ_c,crit,y = π²·E_0,05/λ²_y (wzór 4.2.1.g z ww. normy)

σ_c,crit,y = π²·8000/65,2² = 18,57 MPa,

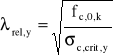
(wzór 4.2.1.c z ww. normy)

,

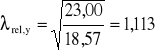
(wzór 4.2.1.e z ww. normy)

β_c - współczynnik dotyczący prostoliniowości elementów (dla drewna litego β_c = 0,2)

k_x = 0,5[1 + 0,2(1,113 - 0,5) + 1,113²] = 1,181

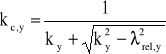
(wzór 4.2.1.a z ww. normy)

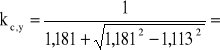
0,634

σ_c,0,d = S/A_d = 30,809·10³/5625 = 5,477 MPa

Stan graniczny nośności prętów osiowo ściskanych należy sprawdzać według warunku 4.2.1.j z PN-B-03150:2000:

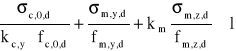
f_c,0,d = f_c,0,k·k_mod/γ_M = 23·0,9/1,3 = 15,92 MPa

Warunek SGN został spełniony.

POLITECHNIKA WROCŁAWSKA

ZAKŁAD BUDOWNICTWA OGÓLNEGO

9

*

---