Układ współrzędnych naturalnych; uzasadnij, że trójka liczb _P, _P, W_P jednoznacznie określa położenie punktu P w przestrzeni względem naturalnego układu współrzędnych.

Układ wsp. naturalnych: związek układu horyzontalnego, będącego lokalnym układem obserwacyjnym na powierzchni Ziemi (taki w którym dokonano obserwacji), z układem globalnym.

* podstawowa oś układu to chwilowa oś obrotu ziemi ( ω ) przechodząca przez pkt. S środka mas ziemi

* płaszczyzna poprowadzona przez pkt. S i jednocześnie prostopadła do chwilowej osi obrotu ziemi to płaszczyzna równika astronomicznego.

* w obserwatorium astronomicznym Greenwich poprowadzono pęk płaszczyzn wertykalnych, zawierających kierunek linii pionu w tymże obserwatorium. Z tego pęku płaszczyzn wybrano tą która jest równoległa do osi wirowania ziemi ϖ i nazwano ją płaszczyzną południka astronomicznego Greenwich.

_p -szer. gegraf.-astronom kąt zawarty między pł. równika, a kierunkiem linii pionu pkt. P.

λ_p -dł. gegraf.-astronom kąt zawarty między pł. południka Greenwich, a pł. południka pkt. P.

W_p -wartość potencjału powierzchni w danym pkt. P

P(ϕ, λ, Wp) ϕ (0°, 90°) λ(0°,360° lub 180° ). Dodatkowo musi być znana chwilowa oś obrotu Ziemi oraz pł. południka zerowego.

1. Uzasadnij, że pomiędzy głównymi promieniami krzywizny elipsoidy obrotowej zachodzi następująca zależność M=N(1-e²)/W².

Promień krzywizny południka M wynosi M=(ds./dB).

Wzór ten możemy przekształcić do postaci:

Różniczkę (dp/dB) wyznaczymy ze wzoru:

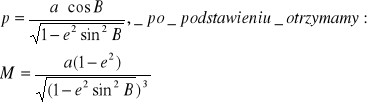
Wyrażenie na promień równoleżnika (p) daje podstawę do wyznaczenia promienia krzywizny w I wertykale. Jeśli skorzystamy z tw. Meusniera (promień krzywizny przekroju ukośnego, mającego wspólną styczną z przekrojem normalnym, może być wyrażony przez zrzutowanie promienia krzywizny przekroju normalnego na kierunek promienia przekroju ukośnego). Wobec tego mamy:

Powtarzające się wzory w mianownikach na M i N, gdzie M=<N oznaczamy przez:

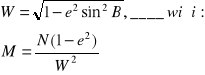
2. Pokaż, że średni promień krzywizny elipsoidy obrotowej jest średnią geometryczną głównych promieni krzywizny.

Prowadząc pęk płaszczyzn przez normalną w dowolnym pkt. na elipsoidzie obrotowej, otrzymamy przekroje normalne elipsoidy. W każdym pkt. powierzchni istnieją takie dwa wzajemnie prostopadłe przekroje normalne, których krzywe charakteryzuję się ekstremalnymi krzywiznami. Nazywa się je przekrojami w kierunkach głównych. Na elipsoidzie obrotowej (z wyjątkiem jej biegunów) jest to kierunek południka geodezyjnego (krzywizna max M^-1) oraz wertykału prostopadłego do południka, zwanego pierwszym wertykałem (krzywizna N^-1).

Krzywiznę dowolnego przekroju normalnego o azymucie A można wyznaczyć na podstawie krzywizn w kierunkach M^-1, N^-1, korzystając z twierdzenia Eulera:

Wzór ten daje podstawy do wyznaczenia średniego promienia krzywizny R_S jako granicy, do której dąży średnia arytmetyczna krzywizn wszystkich przekrojów normalnych w rozpatrywanym pkt. Tworząc sumę nieskończenie wielu promieni krzywizn R_A|₀^2, otrzymamy R_S w postaci średniej wartości całki:

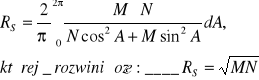
3. Przedstaw na rysunku szerokość geodezyjną i szerokość geocentryczną; wykaż, że maksymalna różnica szerokości geodezyjnej i szerokości geocentrycznej osiąga wartość 11,6'.

z

P*

p

P

b a r

z

  B x/y

a

Szerokość geodezyjna B jest to kąt jaki tworzy normalna do elipsoidy z płaszczyzną równika geodezyjnego. B = (0⁰ - 90⁰)_S^N.

Szerokość geocentryczna  jest to kąt jaki tworzy promień wodzący pkt. P znajdującego się na powierzchni elipsoidy z płaszczyzną równika.

Po przekształceniu wzoru:

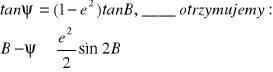
Z tego możemy oszacować:

4. Przedstaw na rysunku szerokość geodezyjną i szerokość zredukowaną; wykaż, że maksymalna różnica szerokości geodezyjnej i szerokości zredukowanej osiąga wartość 5,8'.

z

P*

p

P

b a r

z

  B x/y

a

Szerokość geodezyjna B jest to kąt jaki tworzy normalna do elipsoidy z płaszczyzną równika geodezyjnego. B = (0⁰ - 90⁰)_S^N.

Szerokość zredukowana  jest to kąt jaki tworzy promień wodzący rzutu P* z płaszczyzną równika. Punkt P* otrzymujemy rzutując pkt. P prostą równoległą do osi Oz z powierzchni elipsoidy na kulę o promieniu (a).

Z rys. wynika, że:

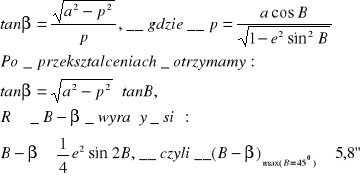
5. Przedstaw równania parametryczne elipsoidy obrotowej.

Biorąc wzory:

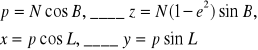
Po przekształceniu otrzymujemy parametryczne równania elipsoidy obrotowej:

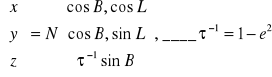
Wprowadzamy jednostkowy wektor normalny elipsoidy (n), oraz diagonalną macierz kształtu F:

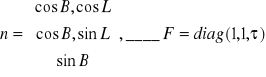
Wówczas równanie parametryczne elipsoidy zapiszemy następująco:

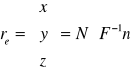
6. Podaj definicję oraz właściwości linii geodezyjnej na powierzchni elipsoidy obrotowej; omów właściwość linii geodezyjnej przedstawioną tzw. równaniem Claitauta; przedstaw przebieg linii geodezyjnej względem wzajemnych przekrojów normalnych.

Linia geodezyjna - jest to najkrótsza odległość pomiędzy dwoma pkt. na pow. i jest to taka linia której normalna główna w każdym pkt. ma kierunek normalnej do powierzchni.

K_g=(r'x r”)*n=0

K_g - krzywizna geod; r' -wektor styczny; r”-wektor krzywizny, n-wektor normalny do pow.

Jest to ogólny zapis właściwości linii geodezyjnej.

Równania różniczkowe I rzędu

dB/ds. = cosA/M B+db

dl/ds = sinA/NcosB MdB A ds

B NcosBdL

L L+dl

Równanie Clairaunta:

Podstawowa własność linii geodezyjnej tzw. równanie Caliraunta linii geodezyjnej NcosBsinA = c = const.

Iloczyn promienia równoleżnika i sinA linii geodezyjnej jest wielkością stałą dla całej linii. Stałą c można interpretować jako promień takiego równoleżnika dla którego linia geodezyjna jest styczna i ma azymut 90^o

Przebieg L.G. na pow. elipsoidy obrotowej:

W ogólnym przypadku normalne do pow. w pkt. P₁ i P₂ są wichrowate (za wyjątkiem południków i pkt. o tych samych szerokościach geodezyjnych)

N

P₂

₁”

s” s s'

₁

_'

P₁ s- linia geod.

s',s”-wzajemne przekroje normalne.

7. Naszkicuj rysunki, z których wynikają wzory różniczkowe linii geodezyjnej pierwszego rzędu; przedstaw te wzory.

B+db

MdB A ds

B NcosBdL

L L+dl

Równania różniczkowe I rzędu:

dB/ds. = cosA/M

dL/ds = sinA/NcosB

Równanie Clairauta linii geodezyjnej:

NcosBsinA = c = const.

Równanie to przedstawia własność L.G. mówiące o tym, że iloczyn promienia równoleżnika I sinusa azymutu linii geodezyjnej jest wielkością stałą dla całej linii.

8. Przedstaw istotę 2 znanych ci metod rozwiązywania trójkątów geodezyjnych.

Trójkątem geodezyjnym nazywamy trójkąt na powierzchni elipsoidy obrotowej utworzony przez 3 łuki linii geodezyjnych.

Przez rozwiązanie trójkąta geodezyjnego rozumiemy obliczenie jego elementów na podstawie znanych 3 elementów (1-go boku i położenia trójkąta na elipsoidzie)

Mając pomierzone kąty A'B'C' wyrównujemy je ze względu na błędy pomiarowe:

=A'+B'+C'-180  P_ R^

A=A'-1/3 B=B'-1/3 C=C'-1/3

Dysponując właściwymi kątami możemy zastosować metodę Legendre'a, additam lub ścisłą:

Metoda Legendre'a: (dł. boku < 90 km)

Mały trójkąt sferyczny można rozwiązać zamieniając go na trójkąt płaski w którym boki pozostają niezmienione a kąty należy zmniejszyć o 1/3 dalej stosując wzory trygono. rozwiązuje się jako trójkąt płaski.

Metoda additamentów:

Polega na zmianie trójkąta sferycznego na płaski w taki sposób że 2 kąty pozostają takie jak na sferze a boki pozostają powiększone o wielkości additamentów liniowych i stosując wzory sinusowe rozwijamy funkcję w szereg.

9. Podaj definicje oraz podstawy klasyfikacji metod obliczania współrzędnych na powierzchni elipsoidy obrotowej.

Zadane wprost: dane(B₁L₁) A₁₂,S₁₂;szukane (B₂L₂), A₂₁.

Zadanie odwrotne: dane(B₁L₁)(B₂L₂);szukane S₁₂A₁₂A₂₁

Met. bezpośrednia: S<20.000 km.

Metoda polega na przeniesieniu (obliczeniu) wsp. pkt. 1 o danych wsp, na drugi pkt. o szukanych współrzędnych, przez rozwiązanie trójkąta elipsoidalnego którego wierzchołki to dwa pkt. i biegun.

Metoda wykorzystująca szeregi potęgowe Legendre'a: Metoda polega na rozwinięciu w szereg Maclarena różnic B,L,A względem parametru naturalnego, którym jest linia geod. Najpowszechniej stosowana met. to met. średniej szerokości Gaussa. Wykorzystuje ona szeregi ale dla pkt. środkowego linii geod. co powoduje, że przy zsumowaniu pochodnych nieparzyste wyrazy zostaną wyeliminowane. S<200 km.

Metoda wykorzystujące pkt. pomocniczy:

W met. tych ze względu na to że trójkąty są wysmukłe (dla krótkich linii geod.) korzysta się z pkt. pomocniczego powstałego w wyniku przekroju normalnego poprowadzonego w pkt. 2 tak aby był prostopadły do południka w pkt.1. S<30 km.

Metoda cięciw elipsoidy:

Trójwymiarowe podejście Mołodeńskeigo;

Metoda polega na rozwiązywaniu trójkątów płaskich utworzonych przez cięciwy elipsoidalne jak trójkąty geodezyjne nowego typu.

Zadanie wprost i odwrotne polega na rozwiązywaniu trójkątów sferycznych.

Metoda całkowania numerycznego:

Algorytm Kivjoja wykorzystujący równania różniczkowe I rzędu oraz równanie Clairauta linii geod. które powinno być zastąpione różniczką azymutu aby algorytm był poprawny dla każdego azymutu

10. Naszkicuj rysunki i objaśnij metodę Clarke'a rozwiązania `zadania wprost'.

B

 L

t

90-B'₂
90-B₂

 L 90-B₂

_ γ

p B'₂

P'₂  

P₂ Rys. 2. b

u A₁₂

Rys. 1

P₁.

B₁

90-B'₂

 L 180-L

P'₂ 90-B₂  T

 γ 

u  90

A₁₂ 180-γ

P₁ s₁₂ P₂ t

p

b

 L

B₂ Rys. 3.

Dysponując współrzędnymi pkt. P obliczamy średni promień elipsoidy w tym pkt. Na kuli o takim promieniu rozwiązujemy mały prostokątny trójkąt sferyczny P₁P₁'P₂ (Rys. 1).

Otrzymujemy przyprostokątne:

Po dodaniu do B₁ wartości (1/2)u można wyznaczyć średni promień krzywizny M_m łuku południka P₁P₂'.

Różnicę szerokości Clarke wyznaczył z prostokątnego trójkąta P₂'BP₂.

Po przekształceniach szerokość pkt. P₂ ma postać:

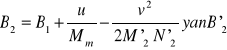
Aby wyznaczyć różnicę długości Clarke wykonał konstrukcję pomocniczą (Rys. 3).

Z rys. sumy odpowiednich kątów w trójkącie (P₂B₂T) i odpowiednich boków trójkąta biegunowego wynoszą 180. Wartość γ to zbieżność południków. Trójkąt (ptb) (Rys. 2) jest niewielkim trójkątem sferycznym i można go rozwiązać z twierdzenia Legendre'a.

Po poprawieniu kątów w trójkącie o (1/3)₁ mamy:

Aby wyznaczyć azymut A₂₁ musimy obliczyć wartość kąta zbieżności południków γ z trójkąta (ptb).

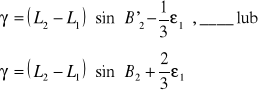
Po wyznaczeni kąta  z trójkąt (P₁P'₂P₂) i zsumowaniu katów w horyzoncie pkt. P₂ otrzymamy:

11. Przedstaw założenia oraz scharakteryzuj podstawowe elementy w rozumowaniu Gaussa w odniesieniu do metody obliczania współrzędnych `średniej szerokości'.

Metoda obliczania współrzędnych zaproponowana przez Gaussa polega na wykorzystaniu szeregów potęgowych Legendre'a, ale w postaci, gdzie pochodne względem parametru naturalnego (s) odnoszą się do pewnego pkt. pomocniczego P_m usytuowanego w połowie długości linii geodezyjnej, a nie do pkt. początkowego P₁. Spłaszczenie elipsoidy sprawia, że współrzędne pkt. P_m i azymut linii w tym pkt. są zazwyczaj różne od wartości średnich.

Po rozwinięciu różnic B₂-B_m i B₁-B_m w szereg potęgowy według propozycji Gaussa i po następnych przekształceniach możemy zauważyć, że wzóry Gaussa zawierają pochodne tylko nieparzystego rzędu. Są przez to o połowę krótsze. Współczynniki przy odpowiednich pochodnych są mniejsze.

W metodzie tej problem polega na wyznaczeniu wartości pochodnych pkt. P_m, którego współrzędnych nie znamy. Dlatego Gauss proponuje zastąpić pochodne w tym pkt. rozwinięciem w szereg Taylora w otoczeniu pkt. P, zachowując tylko wyrazy pierwszego rzędy w tym rozwinięciu.

Po przeprowadzeniu odpowiednich przekształceń otrzymamy wyrażenia Gaussa dla różnic (B₂-B₁), (L₂-L₁) i (A₂-A₁).

Wzory Gaussa można stosować dla s dochodzących do 200 km. Otrzymujemy dokładności obliczeń około 0,0001” dla szerokości i długości, oraz około 0,001” dla azymutów.

Przy rozwiązaniu zadania wprost trzeba stosować podejście iteracyjne, gdyż po prawych stronach wzorów występują nieznane b i l.

Metoda Gaussa dla zadania odwrotnego była najczęściej stosowana do rozwiązywania odwrotnego zadania geodezji wyższej.

12. Wskaż na powiązanie algorytmu całkowania numerycznego w obliczeniu współrzędnych (metody Kivioja) z twierdzeniem Clairauta dla linii geodezyjnej na powierzchni elipsoidy obrotowej.

Metoda całkowania numerycznego Algorytmem Kivioja jest najprostszą, a jednocześni odpowiednio dokładną aby można ją było stosować dla odległości < 200 km. Metoda ta polega na zastosowaniu równań różniczkowych I-go rzędu dla linii geodezyjnej oraz równania Clairauta linii geodezyjnej. Zadanie wprost pozwala rozwiązać sukcesywna realizacja tych związków dla niewielkich np.: 1-o km odcinków linii geodez. Jedynym ograniczeniem tej metody jest zjawisko narastania bł. numerycznych.

Kolejne czynności przy obliczeniu współrzędnych metoda C.N.A. Kiwioja:

• obliczenie długości linii geodezyjnej ds., ds.=(s/n),

• wyznaczenie głównych promieni krzywizny (M_i,N_i) w pkt. wyjściowym (i=P₁),

• wyznaczenie stałej (c) linii geodezyjnej z równania Clairauta,

• wyznaczenie pierwszego przybliżenia przyrostu szerokości δB_i⁽¹⁾,

• wyznaczenie średnich wartości M_i^m,N_i^m, oraz wartości azymutu elementu ds._i w połowie tego elementu (w tym miejscu korzystamy ze stałej (c) wyznaczonej z równania Clairauta),

• po tych obliczeniach uzyskujemy lepsze przybliżenie wartości δB_i oraz δL_i,

• wykonujemy teraz kolejne iteracje do momentu, gdy osiągniemy pkt. końcowy linii geodezyjnej P₂,

• w każdym pkt. pośrednim obliczamy najpierw azymut, a następnie promienie krzywizny M_i i N_i,

• współrzędne geodezyjne pkt. końcowego uzyskujemy przez zsumowanie odpowiednio:

W celu obliczenia azymutu odwrotnego możemy skorzystać ze wzoru:

13. Scharakteryzuj odwzorowanie Gaussa-Krugera i odwzorowanie UTM.

G-K odwzorowanie wiernokątne walcowe poprzeczne. Podział elipsoidy na pasy południkowe o szerokości 3^o dla 1:5000 i 6^o dla skal mniejszych niż 1:10 000; skala na południku osiowym m=1 bez zniekształceń. Linie równych zniekształceń są równoległe do obrazu południka osiowego który odwzorowuje się na linię prostą; w każdym pasie przyjmuje się ukł. wsp. (xy) obraz płd. środkowego x, obraz równika y; środkowe płd. numerowane są kolejno na wsch. od płd. zerowego w Greenwich 0,3,6,9,12.

Dla Polski południki osiowe dla pasów 3⁰ - (15, 18, 21, 24); południki osiowe dla pasów 6⁰ - (15, 21).

Do wsp. y w każdym pasie dodawane jest 500 km aby uniknąć ujemnych wartości y.

UTM jest to pewna modyfikacja odwzorowania G-K; skala południka osiowego m=0,9996; podział na pasy odwzorowawcze 6^o numerowane od1-60 od płd. antyGreenwich PL-34,35; początkiem układu wsp. w każdym pasie jest pkt. przecięcia się południka osiowego z obrazem równika; wsp. y w każdej strefie wynosi Y=[nr strefy] 500km; oś x to obraz płd. osiowego, y obraz równika.

UTM - UNIVERSAL TRANSVERSE MERCATOR PROJECTION.

14. Przedstaw redukcje długości i redukcje kierunków w odwzorowaniu G-K.

Redukcja długości:

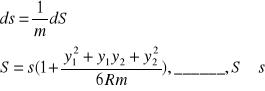
S - na płaszczyźnie

s - na elipsoidzie

y = 0, to południk osiowy, to S = s

R_m - średni promień krzywizny środkowego pkt.

linii.

W miarę oddalania się od południka osiowego wartości redukcji rosną.

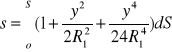
Redukcja kierunków:

Zależność między kątem kierunkowym, a azymutem:

₁₂=A₁₂γ_δ_, ₂₁=A₂₁γ_δ_

elipsoida: płaszczyzna:

południk osiowy obraz południka

O₂ P₂ O₂' P₂'

^ ^δ_δ_ δ_

O₁ P₁

O₁' δ_

P₁'

Suma kątów wewn. fig. na elipsoidzie wynosi 360⁰+

Suma kątów fig. płaskiej wynosi 360⁰+δ_δ_

Zatem δ_δ_, przyjmujemy że: δ_δ_

δ_(

Powierzchnia trapezu P₁', P₂', O₁', O₂' wynosi:

(x₂-x₁)y_m, y_m=(y₁+y₂)/2

Przybliżony wzór na redukcję kierunku:

Wielkość redukcji i jej dokładność zależą od dł. boków, odległości od południka osiowego, azymutu boku, a także od przyjętej szerokości pasów odwzorowawczych.

15. Objaśnij transformację do sąsiednich pasów odwzorowawczych na płaszczyźnie odwzorowania G-K.

Problem transformacji do sąsiednich pasów odwzorowawczych powstaje wtedy gdy opracowywany obiekt leży na granicy pasów odwzorowawczych. Istnieje wówczas konieczność przeliczenia współrzędnych z jednego pasa do drugiego aby można było pracować na wsp. z jednej płaszczyzny odwzorowawczej. Kiedyś wykonywano to za pomocą wzorów i tablic. Opracowano nawet bezpośrednią metodę interpolacji wielomianowej funkcji dwóch zmiennych niezależnych. Obecnie znacznie prościej jest przeliczyć wsp. (xy) z pasa o południku osiowym L₁ na wsp. (BL) zmienić południk osiowy na L₂ i za pomocą funkcji odwzorowawczych przeliczyć wsp. (BL) na (xy) w sąsiednim pasie.

16. Podaj definicję potencjalnego pola wektorowego oraz watunek potencjalności tego pola.

Potencjalnym polem wektorowym nazywamy pole wektorowe w (P) które jest gradientem pewnej funkcji skalarnej V(P) w obszarze (S).

Funkcję skalarną V(P) nazyw. potencjałem pola w (P)

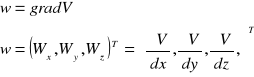
Po wprowadzeniu operatora Hamiltona  (nabla)

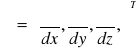
Wzór przybiera postać:

17. Rozpatrz potencjał grawitacyjny punktu materialnego, zbioru punktów materialnych oraz ciała materialnego.

Siła z jaką masa (m) przyciąga inną masę (m'=1) umieszczoną w odległości (l) od masy (m) wynosi:

F - siła, m - masa, l - odległość, G - siła grawitacji,

Potencjał grawitacyjny pkt. materialnego:

Potencjał grawitacyjny zbioru pkt. materialnych:

Potencjał grawitacyjny ciała materialnego:

Zakładamy że:

• gęstość elementu masy σ jest funkcją położenia tego elementu σσ(,,,

• objętość elementu można przedstawić w postaci iloczynu: dddd

Masa elementarna dm jest równa dm=σ d

Z tego otrzymujemy wzór:

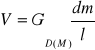
18. Co rozumiesz pod pojęciem zagadnień brzegowych teorii potencjału? Objaśnij pierwsze, drugie i trzecie zagadnienie brzegowe.

Zagadnieniami brzegowymi nazywamy poszukiwanie wartości granicznych lub brzegowych. W geodezji fizycznej można podać związki funkcyjne pomiędzy pochodnymi tych samych parametrów. W celu rozwiązania rów. różniczkowych n-tego rzędu należy podać tyle stałych całkowań jaki jest rząd tego równania czyli n. By otrzymać rozwiązanie szczególne potrzebujemy mieć n-1 wartości początkowych mieszczących się w przedziale zmienności funkcji będącej rozwiązaniem równania.

Pierwsze zagadnienie brzegowe:

Zwane jest również zagadnieniem Dirichleta.

Ma na celu wyznaczenie funkcji harmonicznych (potencjału) na zewnątrz pewnej powierzchni (S) na podstawie granicznych (brzegowych) wartości tych funkcji na powierzchni (S).

Zasada Dirichleta mówi, że dla dowolnie przyjętych wartości granicznych na (S) istnieje pewna funkcja harmoniczna (V), która ma wartości graniczne na powierzchni (S).

Drugie zagadnienie brzegowe:

Ma na celu wyznaczenie wartości potencjału w przestrzeni zewnętrznej lub wewnętrznej względem (S). Na powierzchni (S) zamiast (V) dane są pochodne normalne potencjału (∂V/∂n), względem zewnętrznej normalnej do (S).

Trzecie zagadnienie brzegowe:

Na powierzchni (S) znana jest kombinacja liniowa potencjału (V) i jego pochodnej w kierunku normalnej zewnętrznej do (S) w postaci hV+(k(∂V/∂n)), (h , k) - stałe. Zagadnienie to ma szczególne zastosowanie w geodezji fizycznej (model wyznaczenia undulacji geoidy z anomalii grawimetrycznych).

19. Wielomiany Legendre'a a dołączone funkcje Legendre'a: w czym tkwi istota róznicy tych funkcji? Naszkicuj charakterystyczne wykresy wielomianów Legendre'a P₀, P₁, P₂, P₃, P₄. Co to są tzw. powierzchniowe (elementarne) harmoniczne sferyczne i do czego się je wykorzystuje?

Funkcje Legendre'a to (n+m)-te pochodne wielomianu (x²-1), gdzie m i n są parametrami całkowitymi i mogą być tylko wartościami naturalnymi.

Dla wartości m=1,2,...n (m≠0) funkcje  nazywa się dołączonymi funkcjami Legendre'a, lub stowarzyszonymi.

Gdy m=0, to funkcje Legendre'a nazywane są wielomianami Legendre'a, lub funkcjami głównymi Legendre'a.

Dołączone funkcje Legendre'a można wyrazić przez wielomiany Legendre'a na podstawie wzoru:

Parzyste wielomiany (P₀ P₂ P₄...) wyrażają symetrię.

Nieparzyste wielomiany (P₁ P₃ P₅...) wyrażają asymetrie. Czym większy rząd pochodnej to zwiększa się okres o połowę.

P_n

P0		1 P0
P2		0,5	P1 P2
P4			P3
-1 P3	-0,5	-0,5	0,5 1 P4
P1
		-1 cos

Powierzchniowe harmoniczne sferyczne:

P.H.S. to iloczyn funkcji  i wyrażeń w postaci cosm oraz sinm

P_nm(cos*cosm  c_nm(,

P_nm(cos*sinm  s_nm(,

Współczynniki c_nm, s_nm można wyznaczyć na podstawie tzw relacji ortogonalności funkcji Legendre'a.

P.H.S. wykorzystuje się do przedstawienia rozkładu potencjałów.

20. Omów te własności wielomianów Legendre'a, które pozwalają na ich zastosowanie do rozwinięcia potencjału grawitacyjnego w szereg harmonicznych strefowych.

Rozwinięcie harmoniczno sferyczne to iloczyn funkcji  i wyrażeń w postaci cosm oraz sinm

P_nm(cos*cosm  c_nm(,

P_nm(cos*sinm  s_nm(,

Współczynniki c_nm, s_nm można wyznaczyć na podstawie tzw relacji ortogonalności funkcji Legendre'a.

Warunek ortogonalności dla f. Legendre'a i wielomianów  oznacza, że całka iloczynu 2 różnych funkcji lub wielomianów Legendre'a w granicach

(-1,1) jset równa 0.

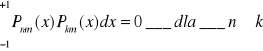
Całka iloczynu dwóch takich samych funkcji lub wielomianów:

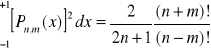
Jeżeli harmoniczne sferyczne podzielimy przez:

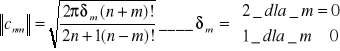
to otrzymamy znormalizowane harmoniczne sferyczne

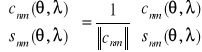
Ortogonalność funkcji Legendre'a - normalizacja harmonicznych sferycznych.

21. Przedstaw harmoniczne sferyczne: strefowe, sektorowe i tesseralne; powiąż te rodzaje harmonicznych sferycznych z wyrażeniami przedstawiającymi rozwinięcia potencjału grawitacyjnego odnoszące się do szczególnych przypadków rozkładu masy na powierzchni.

Powierzchnie harmoniczne sferyczne są to iloczyny funkcji Legendre'a i wyrażeń w postaci cos m

i sin m

P_nm(cos cos m = c_nm(,,

P_nm(cos sin m = s_nm(,,

Powierzchniowa funkcja sferyczna jest sumą kombinacji liniowych harmonicznych sferycznych:

C_nm i S_nm - dowolne stałe.

Gdy m≠n≠0 i m<n to harmoniczne tworzą obraz mozaiki i nazywamy je harmonicznymi tesseralnymi.

Gdy m=0 to otrzymujemy wartości 0 dla n równoleżników i nazywamy je harmonicznymi strefowymi. Są one zależne tylko od  i  po zamianie zmiennych.

Gdy m=n to otrzymujemy wartości 0 dla 2n południków nazywamy je harmonicznymi sektorowymi. Są one zależne tylko od 

Wzór wyrażający potencjał grawitacyjny:

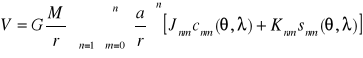
Gdy założymy symetrie rozkładu masy względem osi obrotu (niezależność rozkładu masy względem wsp. , to wyeliminujemy ze wzoru harmoniczne sektoralne i tesselarne.

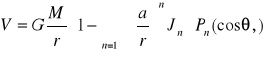
Wzór ten odpowiada symetrycznemu rozkładowi masy względem osi obrotu. Harmon. nieparzystych stopni wyrażają niesymetrię rozkładu masy względem pł. równika.

Gdy pozostawimy tylko harmoniczne sfer. parzyste (2n) to:

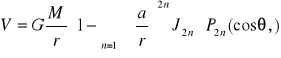
Wzór ten odnosi się do potencjału grawitacyjnego bryły obrotowej pod względem rozkładu masy (symetria względem osi obrotu) i symetrycznej względem równika.

22. Pokaż na rysunku, a następnie objaśnij słowami użyteczność wielomianów P₂₀, P₃₀ do `modelowania' spłaszczenia Ziemi oraz niesymetrii rozkładu mas Ziemi względem płaszczyzny równika.

+ +

+

+

P20 P30

Dla m=0 wielomiany Legendre'a n-tego stopnia będą miały n wartości zerowych w przedziale 0 , zmieniając znak n razy.

Wielomian P₂(cos wyraża symetrię względem równika, natomiast P₃₀(cos asymetrię.

We wzorze na potencjał:

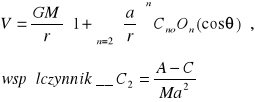
C - moment bezwładności na równiku,

A - moment bezwładności na biegunie,

M - masa Ziemi,

a - duża półoś elipsoidy,

r - promień wodzący. Współczynnik C₂ jest związany ze spłaszczeniem bryły poprzez moment bezwładności.

23. Pokaż zasadnicze różnice pomiędzy harmonicznymi sferycznymi a harmonicznymi elipsoidalnymi.

Harmoniczne sferyczne:

Harmoniczne sferyczne to iloczyn funkcji  i wyrażeń w postaci cosm oraz sinm

P_nm(cos*cosm  c_nm(,

P_nm(cos*sinm  s_nm(,

Współczynniki c_nm, s_nm można wyznaczyć na podstawie relacji ortogonalności funkcji Legendre'a.

Wykresy harmonicznych sferycznych

P_n

P0		1 P0
P2		0,5	P1 P2
P4			P3
-1 P3	-0,5	-0,5	0,5 1 P4
P1
		-1 cos

Harmoniczne elipsoidalne:

Harmoniczne elipsoidalne przedstawione są iloczynami o postaci:

P_nm(cos*cosm

P_nm(cos*sinm

Są one odpowiednie do harmonicznych sferycznych.

Wykresy harmonicznych elipsoidalnych:

Q_n

		1,4
Q2		0,7 Q3	Q0
			Q1
-1 Q3	-0,5	-0,7 Q2	0,5 1
Q0	Q1
		-1,4 cos

Zasadniczą różnicą pomiędzy harmonicznymi sferycznymi ,a elipsoidalnymi jest to, że  oznacza w H.S. odległość biegunową równą dopełnieniu do 90⁰ szerokości geocentrycznej, a  w H.E. jest dopełnieniem do 90⁰ szerokości zredukowanej.

24. Przy jakich założeniach elipsoida ekwipotencjalna reprezentuje pole normalne siły ciężkości Ziemi?

Elipsoida obrotowa jest stosowana jako pow. odniesienia dla wszystkich zadań geodezyjnych. Związanych z polem siły ciężkości (anomalie grwim.), odstępy geoidy od elipsoidy, odchylenia pionu, redukcje sieci geodezyjnych, badania figury Ziemi. Dlatego przyjęto jako model pola siły ciężkości elipsoidę ekwipotencjalną o następujących warunkach;

- rozmiar i kształt elipsoidy (a,f) są tak dobrane, aby pow. elipsoidy była jak najlepszą aproksymacją geoidy; - masa elipsoidy równa masie ziemi;

- prędkość kątowa wirowania elipsoidy wokół małej osi jest równa prędkości wirowania Ziemi ω;

- powierzchnia przyjętej elipsoidy ma być z definicji pow. ekwipotencjalną, o potencjale U₀ równym rzeczywistemu potencjałowi siły ciężkości geoidy W₀

Model pola siły ciężkości reprezentowanego przez tę elipsoidę nazywa się normalnym polem siły ciężkości.

Takie założenia pozwalają jednoznacznie określić potencjał normalny U w przestrzeni gdy znany jest potencjał U₀=const. pow. ekwipotencjalnej. Rozkład masy M wew. tej pow. nie musi być znany gdyż Stokes określił rozkład potencjału grawitacyjnego w przestrzeni zew. dla dowolnego rozkładu masy objętego jakąś jedną znaną pow. ekwipotencjalną tej masy. Ponieważ znamy prędkość wirowania ω to możemy wykorzystać to twierdzenie Stokesa do potencjału siły ciężkości.

25. Przedstaw uproszczona postać twierdzenia Clairauta wiążącego spłaszczenia geometryczne i grawimetryczne; podaj interpretację wzoru opisującego twierdzenie Clairauta.

f+f*=((ω²b)/γ_a)(1+(e'p_b'/2p_b))

gdzie e'=E/b

f=(a-b)/a spłaszczenie geometryczne

f*=(γ_b-γ_a)/γ_a spłaszczenie grawimetryczne

γ_a przyśpieszenie normalne na równiku;

γ_b przyśpieszenie normalne na biegunie

Twierdzenie Clairauta pokazuje możliwości wyznaczenia spłaszczenia geometrycznego f za pomocą czysto dynamicznych wielkości (przyśpieszenia, siły ciężkości γ_a γ_b), które określają f, oraz parametru q który zależny jest od wielkości wirowania wymiaru elipsoidy i masy Ziemi. Z twierdzenia wynika że na podstawie wielkości dynamicznych można wyznaczyć masę Ziemi bo q=(ω²a²b)/(GM).

26. Przedstaw i omów przybliżony wzór na przyspieszenie normalne siły ciężkości.

Dokładność wzoru szacuje się na około 0,1 mgal.

f₄ - funkcja spłaszczenia geometrycznego. i graw.

f=(a-b)/a - spłaszczenie geometryczne,

f*=(γ_b-γ_a)/γ_a - spłaszczenie grawimetryczne,

B - szerokość geodezyjna,

γ_a - przyspieszenie normalne na równiku,

γ_b - przyspieszenie normalne na biegunie,

γ - przyspieszenie normalne dla określonej szerokości geodezyjnej (B)

γ = gradU - przys. norm. siły ciężkości

U - potencjał normalny.

27. Omów równanie Brunsa przedstawiające gradient pionowy siły ciężkości.

Gradient pionowy siły ciężkości:

grad g=(∂g/∂h)= (∂g/∂z)=-W_zz

Równanie Brunsa:

4πGσ - współczynnik redukcji Bouguera ze względu na płytę. W przestrzeni zewnętrznej elipsoidy 4πGσ = 0.

H* - średnia krzywizna na powierzchni elipsoidy.

g - przyspieszenie,

G - stała grawitacji,

σ - gęstość skorupy,

ω - prędkość wirowania ziemi,

∂g/∂h - gradient pionowy siły ciężkości wykorzystywany jest w redukcji wolnopowietrznej.

28. Jak wyraża się przyspieszenie normalne ponad elipsoidę ekwipotencjalną.

Gradient pionowy siły ciężkości:

grad g=(∂g/∂h)= (∂g/∂z)=-W_zz

(∂g/∂h)= -2gH*+4πGσ-2ω² - równanie Brunsa

Dla niewielkiej (h) dla γ mamy ∂γ/∂h= -γ(1/M+1/N)-2ω² Rozwijając (1/M,1/N) w szereg według potęg spłaszczenia (f) i zastępując (ω) przez (q) otrzymamy wzór określający przyspieszenie normalne na określonej wysokości w funkcji (γ,a,f,g,B,h)

Po wykorzystaniu wzoru Brunsa mamy:

29. Przeanalizuj pochodne drugiego rzędu potencjału normalnego.

Drugie pochodne potencjału normalnego w kierunkach osi układu kartezjańskiego związanego z pkt. na pow. ekwipotencjalnej. Pomiar rzeczywistych wartości pochodnych drugiego rzędu za pomocą wagi skręceń dawał wyznaczenie łączne różnic

wielkość krzywiznowa U_Δ=U_yy-U_xx Dla elipsoidy ekwipotencjalnej 1/M= -U_xx/γ, 1/N= -U_yy/γ

U_zz=gradγ wynika z rów. Burnusa i jest to -∂γ/∂h

U_xz=(∂γ/∂x)=(∂γ/∂B)*(∂B/∂x)

U_yz=0 gdyż U_yz=(∂γ/∂y)=(∂γ/∂L)*(∂L/∂x), a ∂γ/∂L=0 na elipsoidzie ekwipotencjalnej. Spowodowane jest to symetralną modelu pola normalnego względem osi obrotu (nie zależą od L). Zatem i U_xy=0 wielkość krzywiznowa powierzchni sferoidy. Ponieważ pochodne po λ=0 zatem U_xy=0 i U_yz=0 natomiast linia pionu w południku to linia płaska w płaszczyźnie południka.

30. Co to jest Geodezyjny System Odniesienia 1980 GRS'80? Uzasadnij, że 4 tzw. stałe standardowe stanowią kompletny zbiór danych do zdefiniowania pola normalnego siły ciężkości.

Geodezyjny System Odniesienia GRS 1980 jest to nowy system odniesienia który zastąpił Geodezyjny System Odniesienia z roku 1967 przyjęty w Lucernie.

GRS'80 jest także oparty na teorii geocentrycznej elipsoidy ekwipotencjalnej zdefiniowanej przez następujące stałe standardowe:

• równikowy promień Ziemi:

a = 6.378.137 m

• geocentryczna stała grawitacyjna Ziemi (włączając atmosferę):

GM = 3.986.005 x 10⁸ m³ s ^-2

• dynamiczny współczynnik kształtu Ziemi, wyłączający stałe deformacje pływowe:

J₂ = 108.263 x 10 ^-8

• kątowa prędkość Ziemi:

 = 7.292.115 x 10 ^-11 rad s ^-1

Wyznaczenie wartości (dynami. i geometr.) potrzebnych do obliczeń związanych z elipsoidą odniesienia.

Wyliczenie e:

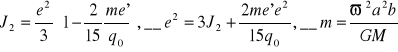
Gdy be' = ae to:

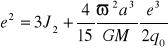
e² wyznaczamy iteracyjnie.

Wyliczenie potencjału normalnego elipsoidy U₀:

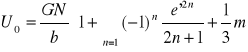
31. Przyspieszenie normalne na sferoidzie Helmerta. Opisz procedurę jaką zastosował Helmert do wyznaczenia współczynników we wzorze na przyspieszenie normalne.

Helmert pomierzył przyspieszenie siły ciężkości g na ok. 1400 pkt. o znanych szerokościach geograficznych ϕ i wysokościach nad poziomem morza H. Wartości g odniósł do pkt. fundamentalnego w Poczdamie w którym wyznaczył wcześniej met. wahadłową wartość bezwzględną przyśpieszenia siły ciężkości (jednakże z bł. 14 mgali) Następnie Helmert zredukował g na geoidę za pomocą red. wolnopowietrznej. Mając taki zbiór pkt. Helmert dokonał aproksymacji geoidy sferoidą normalną narzucając warunek minimum sumy kwadratów anomalii grawimetrycznych.

Otrzymał ostatecznie wzór który różni się od GRS'80 tylko dokł. wyznaczenia współczynników.

32. Omów w zarysie geodezyjne efekty zjawisk pływowych.

Zjawiska pływowe są to zmiany ziemskiej siły grawitacji powodowane siłami przyciągania ciał niebieskich. Same te siły nazywamy siłami pływowymi. Zjawiska pływowe są powodowane przyciąganiem Słońca i Księżyca.

Wynikiem sił pływowych są:

• pływy skorupy ziemskiej,

• przypływy i odpływy oceanów i mórz.

Efekty zjawisk pływowych:

• pływowa zmiana wysokości elipsoidalnej δH:

spowodowana jest ona elastycznymi odkształceniami radialnymi skorupy ziemskiej,

• pływowa zmiana przyspieszenia siły ciężkości δg:

poprawka pływowa do mierzonego przyspieszenia siły ciężkości Pg.

• pływowa zmiana wysokości ortometrycznej H^O:

poprawka pływowa do wysokości ortometrycznej PH^O,

• wysokości normalnej H^N:

poprawka pływowa do wysokości normalnej PH^N,

• pływowa zmiana długości s:

są one rzędu (s x 10^-8), a więc nie ma potrzeby ich uwzględniania w codziennych pomiarach geodezyjnych,

• pływowa zmiana kątów poziomych:

poprawki pływowe kątów poziomych osiągają wartości o kilka rzędów mniejsze od błędów pomiarowych,

• pływowa zmiana odchyleń pionu:

poprawki pływowe składowych odchylenia pionu (w południku i pierwszym wertykale) P i P,

• pływowa zmiana różnic wysokości δh:

poprawka pływowa niwelacji na 1 km ciągu niwelacyjnego Ph.

33. Podaj definicję potencjału zakłócającego oraz uzasadnij, że potencjał zakłócający jest funkcją harmoniczną.

Różnicę potencjału zakłócającego siły ciężkości W_rp i potencjału normalnego U_rp nazywa się potencjałem zakłócającym T_rp. T_rp= W_rp-U_rp

Potencjał zakłócający w pkt. P podobnie jak potencjał rzeczywisty i normalny jest f. położenia pkt. w przestrzeni. Zarówno potencjał rzeczywisty i normalny zawierają ten sam potencjał odśrodkowy zatem z ich różnicy zostanie on wyeliminowany. Zatem pot. zakłócający T jest potencjałem grawitacyjnym i w przestrzeni zew. jest on funkcją harmoniczną ponieważ spełnia rów. Laplace'a T_rp=0. Za pomocą potencjału zakłócającego bada się lokalne nieregularności rozkładu rzeczywistego pola siły ciężkości.

34. Objaśnij podstawowe równania geodezji fizycznej przedstawiając interpretację poszczególnych jego wyrazów. Jak rozumiesz `przybliżenie sferyczne' podstawowego równania.

Δg= -(∂T/∂n)+(1/γ)*(∂γ/∂n)*T równanie to stanowi tzw. trzecie zagadnienie brzegowe geod. fiz. gdyż jest to kombinacja linowa potencjału zakłócającego i jego pochodnej w kierunku normalnej do pow. elipsoidy ekwipotencjalnej Δg=δg+U_zzN -∂T/∂n=δg=g₀-γ

-∂T/∂n - zakłócenie geometryczne lub inaczej właściwa anomalia grawimetryczna bo

γ-przyśpieszenie normalne na geoidzie;

g₀ - rzeczywiste przyśpieszenie;

Δg anomalia grawimetryczna;T potencjał zakłócający

Rów. to wiąże ze sobą zakłócenia grawimetryczne z anomaliami grawimetrycznymi oraz z wysokościami geoidy względem elipsoidy.

Przybliżenie sferyczne jest to zastąpienie powierzchni elipsoidy ekwipotencjalnej powierzchnią kuli o takiej samej objętości. Polega ono na: zaniedbaniu odchyleń pionu przy różniczkowaniu bo kierunek normalnych do geoidy i elipsoidy zastępuje się kierunkiem promienia kuli; zastąpienie rzeczywistego gradientu pionowego przyśpieszenia normalnego gradientem przeciętnym dla Z. jako kuli.

35. Omów wzór Stokesa.

Przedstawia wysokość geoidy ponad elipsoidą ekwipotencjalna poprzez anomalie grawimetr. znane dla całej Ziem. Wynika on z założenia że potencjał zakłócający jest f. harmoniczną czyli ΔT=0, żadne masy nie znajdują się ponad geoidą, a masa Ziem. po redukcji musi być równa całkowitej masie Z. Stokes przyjął że masa elips ekwi.= masie geoidy, środek elipsoidy pokrywa się ze środkiem mas Ziem., osie główne momentów bezwładności pokrywają się.

Wzór Stokesa ma postać::

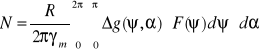
N - wysokość geoidy,

R - średni promień Ziemi

γ - normalna wartość siły ciężkości,

 - odległość sferyczna (wielkość kątowa <0,>

 - azymut wyznaczający kierunek łuku  względem południka pkt. P <0,2>

g - anomalia siły ciężkości

Błąd wyznaczenia < 1m.

36. W jakim związku ze wzorami Stokesa pozostają wzory Vening-Meinesza? Przedstaw i omów te wzory.

θ

θ dN geoida

N ds N

elipsoida

θ= -dN/ds., gdzie:

dN - odstęp geoidy od elipsoidy,

θ - odchylenie piony (odchylenie geoidy względem elipsoidy ekwipotencjalnej). Jest to kąt zawarty pomiędzy normalną do geoidy i odpowiednią normalną do elipsoidy ekwipotencjalnej.

Całkowite odchylenie pionu rozkłada się na dwie składowe w południku ξ i w pierwszym wertykale η. Z wzoru Stokesa wyznaczane są pochodne ∂N/∂φ ∂N/∂λ. Wzory Vening-Meineszas służą do wyznaczenia składowych odchyleń pionu na podstawie anomalii grawimetrycznych

37. Przedstaw redukcję wolnopowietrzną przyspieszenia siły ciężkości. Uzasadnij, że anomalie grawimetryczne wolnopowietrzne mogą być stosowane w zagadnieniach związanych z całką Stokesa.

Redukcja wolnopowietrzna (Fay'a) wyraża wpływ wysokości stanowiska pomiarowego pkt. P ponad geoidą na wartość pomierzonego przyspieszenia siły ciężkości.

W wyniku R.W. geoida zostanie zregularyzowana, tzn. żadne masy nie będą się znajdowały poza jego powierzchnią. Przed wykonaniem R.W. wprowadza się poprawkę terenową. Jest to konieczne, bo inaczej okaże się, że masy położone powyżej horyzontu rozpatrywanego pkt. pozostaną poza geoidą.

-(dg/dh) - gradient pionowy przyspieszenia S.C.

H - wysokość nad geoidą.

δg_F=0,3086*H [mgal/m], H [m].

Gradient pionowy:

Znak redukcji jest taki sam jak znak wysokości.

Efekt pośredni: zniekształcenie geoidy na skutek redukcji. Odstęp cogeoidy od geoidy rzadko przekracza 1 m. dlatego tą redukcję stosujemy przy zagadnieniach redukcji geoidy (H=1km - odstęp=6cm, H=4km - odstęp=94cm).

38. Poprawka terenowa do pomierzonych wartości siły ciężkości.

Poprawka terenowa polega na rachunkowym zrównaniu terenu w otoczeniu stanowiska pomiarowego w taki sposób aby poprawiona wartość przyśpieszenia siły ciężkości odnosiła się do terenu płaskiego.

Poprawka terenowa oparta jest na zasadzie potencjału przyciągania walca, oblicza się ją dla promieni od kilkunastu do 30 km od stanowiska gdyż wpływ stref dalszych może być ujemny spowodowany zakrzywieniem powierzchni ziemi, poprawkę terenową wprowadza się jako pierwszą do pomiarów g. Redukcja topograficzna to rachunkowe usunięcie płyty grubości = wysokości stanowiska pomiarowego ponad geoidą i nieskończonym promieniu po uwzględnieniu sferycznego kształtu.

39. Objaśnij redukcję grawimetryczną Bouguera (za płytę)

Redukcja Bugera - stosuje się gdy teren jest płaski lub gdy została wprowadzona poprawka terenowa,

* przyciąganie płyty Bugera - jest to przyciąganie warstwy zawartej pomiędzy geoidą a pow. ekwipotęcjalną pkt. pomiarowego,

* płytę Bugera traktuje się jako walec o wys. H i równej grubości płyty i promieniu (a) dążącym do nieskończoności Rg= - 2πGσH,

* usunięcie płyty Bugera powoduje zmniejszenie przyśpieszenia siły ciężkości,

* redukcję tę nazywa się niepełną gdyż sprawia, że po usunięciu płyty punkt pomiarowy będzie miał przyśpieszenie takie jakby znajdował się na wysokości H i dlatego trzeba wprowadzić redukcję wolnopow,

* redukcja Bugera regularyzuje zatem geoidę tak, że żadne masy nie będą wystawały poza nią, a nawet szczątkowo nieusunięte fragmenty płyty spowodowane niedokładnym (d) zostaną wepchnięte pod geoidę,

* redukcja Bugera ma duże zastosowanie do wyszukiwania kopalin użytkowych (przez anomalie Bugera ),

* do badania figury ziemi anomalia Bugera nie może być stosowana ze względu na zmianę masy geoidy spowodowane redukcją Bugera.

40. Przedstaw kolejne etapy redukcji grawimetrycznej Poincarego i Preya.

Etapy:

• Wprowadzenie poprawki terenowej co powoduje że zostaje uformowana płyta Bugera o wysokości H;

• Usunięcie płyty Bugera -co powoduje że pkt. uzyskuje przyśpieszenie takie jakby był zawieszony w próżni na wysokości H ponad geoidą;

• Wprowadzenie redukcji wolnopowietrznej;

• Przywrócenie przyciągania płyty Bugera;

• przywrócenie topografii, czyli wprowadza się poprawkę terenową dla pkt. położonego pod płytą.

Zastosowanie:

• do wyznaczenia wysokości ortometrycznych,

• do redukcji pomiarów przyśpieszenia w szybach wiertniczych,

• do redukcji pomiarów grawimetrycznych wykonywanych pod pow. wody na morzach i oceanach.

41. Wysokości dynamiczne i poprawki dynamiczne. Podaj definicję i objaśnij właściwości wysokości wyrażonych w tym systemie.

Wys. dynam. pkt P otrzymujemy dzieląc ujemną wartość różnicy potencjału W_P w pkt P i W_O na geoidzie przez wartość przyspieszenia normalnego na szerokości B=45⁰

H^d_P =(-W_P-W_O)/γ₀⁴⁵

Wykorzystuje się do wyrażenia innych poprawek w innych systemach wysokości.

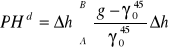
Wys. dynam. i popr. dynam. są wyznaczane ściśle na podstawie pomierzonych różnic wysokości i przyspieszenia siły ciężkości. Poprawki dynamiczne nie mają żadnej interpretacji geometrycznej. Bardzo ważną właściwością tych wysokości jest to, że pkt. położone na tej samej powierzchni ekwipotencjalnej mają taką samą wys. dynam. System wys. dynam. nie uwzględnia nierówności powierzchni ekwipotencjalnych

Zastosowanie: technika, budownictwo wodne, projekty na bardzo dużych obszarach (gdzie wymagana jest duża dokładność projektowania spadków)

42. Przedstaw wysokości ortometryczne Nithammera i Helmerta.

Wys. orto. jest to odległość pkt. fizycznej pow. Ziemi od geoidy mierzona wzdłuż linii pionu (posiada interpretację geom.).

Wys. orto. H=C/g, gdzie C=(W_O-W_P)

C - liczba wyrażająca pracę w polu potencjalnym;

g - przeciętna wartość przyspieszenia siły ciężkości wzdłuż linii pionu.

Podejście Neithammera:

Jest ścisłym podejściem wyznaczenia g (uwzględnia też przeciętne gęstości mas σ_a σ_b na odcinkach linii pionu), co jest prawe nie możliwe do uzyskania. Do wyznaczenia przeciętnej (g) wzdłuż linii pionu pkt A i B Nithamer proponuje wykorzystanie redukcji Poincerego-Preya w połowie wysokości (H/2).

g=g+(δg_F/2) -δg_B+δg_t-δg'_(t/2)

δg'_(t/2) - poprawka terenowa w połowie wysokości uwzględnia gęstości skorupy ziemskiej a także jej ukształtowanie.

Podejście Helmerta:

Jest podejście przybliżonym. Helmert uprościł wzór. Zrezygnował z wyznaczenia poprawek terenowych, gdyż były one z reguły niewielkie.

Przybliżone wysokości ortometryczne.

H_m=(1/2)(H_i+H_i-1)

Gdy przyjmiemy dla całego obszaru jednakową gęstość _A=_B=, to:

43. Przedstaw analizę dokładności wyznaczania wysokości ortometrycznych.

H=(-W_P-W_O)/g = H=c/g po zróżniczkowaniu otrzymamy δH= -H/g *δg. Przy założeniu że g=1000gali otrzymamy δH≈δg stąd wniosek że dla H=1km δH [mm]≈δg [mgali]

bł. przeciętnej wartości g

Zmiana przyspieszenia przeciętnegog będzie związana ze zmianami gęstości δg [mgal] ≈ 42,4 δσ [g*cm^-3]

Gdy δσ=0,1g*cm^-3 to δg = 4,2 mgal - obciąży to 1 km wys. ortom. błędem δH = 4,2 mm.

Gdy Max δσ=0,6g*cm^-3 to δg = 25.4 mgal - obciąży to 1 km wys. ortom. błędem δH = 25,4 mm.

44. Jakie parametry pola siły ciężkości umożliwiaja wyznaczenie krzywizny linii pionu?

`Elementarny' sposób wyprowadzenia wzoru na krzywiznę linii pionu w funkcji przyspieszenia siły ciężkości i jego pochodnych:

Przyrost potencjału dW:

dW = -g_AdH_A = -g_BdH_B, gdzie:

g_A i g_B - przys. siły ciężkości w pkt. A i B,

dH_A i dH_B - różniczki wysokości.

Po przekształceniu otrzymujemy:

g_A - g_B zastąpimy W_XZdx, bo g_B = g_A + W_XZdx

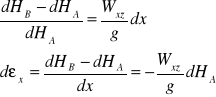
Krzywiznę linii pionu przedstawiamy wzorami:

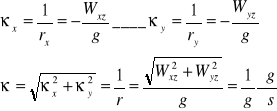
Wektor K.L.P. leży w płaszczyźnie ściśle stycznej do linii pionu.

Zastosowanie:

Całkując wyrażenie dε_x wyznaczymy obrót stycznej do linii pionu spowodowanej krzywizną. W południku oznacza to redukcję szerokości astronom. d z fiz. pow. Ziemi na geoidę. Aby otrzymać redukcję dł. astro. dλ

Należy wartość w pierwszym wertykale zrzutować na płaszczyznę równika.

K.L.P. stosujemy do redukcji kątów poziomych i azymutów oraz redukcji długości.

45. Zaprezentuj zasadnicze etapy procedury Helmerta dotyczącej wyznaczenia i orientacji elipsoidy stanowiącej najlepszą aproksymację geoidy na pewnym obszarze.

Czynność ta polega na spełnieniu warunku:

przez względne odchylenia pionu (zależne od elipsoidy odniesienia) w stacjach astronomicznych sieci.

Etapy procedury:

• przyjęcie dużej półosi elipsoidy a₀ i spłaszczenia f_o za dane wyjściowe do wyznaczanej elipsoidy,

• w pkt. wyjściowym (przyłożenia elipsoidy) wyznaczamy współrzędne (',') i redukujemy je na geoidę (₀,₀), ze względu na krzywiznę linii pionu,

• w tym pkt. wyznaczamy składowe grawimetrycznego odchylenia pionu (₀^g,₀^g) ze wzorów Vening-Meinesza, na podstawie map wolnopowietrznych anomalii grawimetrycznych,

• współrzędne pkt. przyłożenia mają postać: B₀=₀₀^g i L₀=₀-₀^gsec₀.

• można powiedzieć, że w pkt. przyłożenia kierunek normalnej do definiowanej elipsoidy odniesienia pokrywa się z kierunkiem normalnej do elipsoidy ekwipotencjalnej. Gdy pkt. przyłożenia będzie znajdował się w obszarze o małych zakłóceniach grawimetrycznych to przyjmiemy zerowe wartości odchyleń linii pionu i: B₀=₀ i L₀=₀

• w pkt. przyłożenia wyznaczamy ze wzorów Stokesa (N₀)-wysokość geoidy względem elipsoidy normalnej. Możemy również przyjąć N₀=0. Z tego założenia wynika, że powierzchnie elipsoidy odniesienia i geoidy w pkt. przyłożenia są styczne,

• aby dokonać orientacji elipsoidy musimy pomierzyć astronomicznie azymut boku wyjściowego ('). Redukuj. go kolejno na geoidę (₀) i na elipsoidę (A₀),

• bok wyjściowy (s') pomierzony w sieci, redukujemy na elipsoidę (s₀),

• obliczenie współrzędnych pkt. w ciągach wychodzących z pkt. głównego (B₀,L₀) (zadanie wprost), aż do kolejnej stacji astronomicznej (B_i,L_i). W i-tej stacji astronomicznej mamy zaobserwowane i zredukowane na geoidę współrzędne (_i,_i). Możemy teraz obliczyć względne odchylenia pionu: _i =_i B_i i _i =(_i -L_i)cos_i,

• teraz możemy wyznaczyć parametry przedstawiające elipsoidę odniesienia względem geoidy: ₀, ₀, N₀, a, f.

46. Co to jest względne odchylenie pionu? Jak można wyznaczyć wartości względnych odchyleń pionu w punktach nie będących stacjami astronomicznymi?

Względne odchylenia pionu jest to kąt zawarty między normalną do geoidy, a normalną do elipsoidy odniesienia. W.O.P. wyznaczane są na podstawie pomiarów (,) w stacjach astronomicznych i anomalii grawimetrycznych.

    B,

  (  Lcos

Gdy punkty nie są stacjami astronomicznymi, to odchylenia pionu można wyznaczyć poprzez interpolację liniową różnic  i  pomiędzy stacjami astronomicznymi według wzorów:

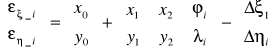
Do tego celu trzeba mieć minimum 3 stacje astronomiczne, aby na podstawie  i  wyznaczyć 6 współczynników interpolacyjnych: x₀, y₀, x₁, y₁, x₂, y₂.

Gdy mamy więcej niż 3 stacje, to układ równań rozwiązujemy poszukując najlepszego dopasowania obu systemów odchyleń pionowych: _^minimum.

Z powyższych równań wyznaczamy różnice _j i _j, dla wszystkich punktów sieci geodezyjnej (j).

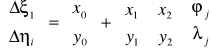
Następnie obliczamy względne odchylenia pionu dla każdego pkt. dodając wyinterpolowane różnice do odchyleń grawimetrycznych.

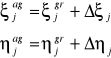
47. Objaśnij procedurę niwelacji astronomiczno-grawimetrycznej. Jakie znaczenie we współczesnej problematyce geodezji ma ta niwelacja?

Niwelacja Astronomiczno-grawimetryczna: oparta jest na zasadzie wyznaczenia wysokości geoidy względem elipsoidy odniesienia w pkt. sieci astro-geod., na podstawie odchyleń pionu wyznaczonych za pośrednictwem metody grawimetrycznej.

Dzięki tej niwelacji ze wzorów Vening-Meinesza możemy wyznaczyć bezwzględne odchylenia pionu, po wykorzystaniu w nich anomalii wolnopowietrznych z całej Ziemi.

Wykorzystanie anomalii z ograniczonego obszaru jest bardzo pomocne w interpolacji względnych odchyleń pionu.

Błąd różnicy wysokości geoidy w pkt. odległych o 30 km nie przekracza 8 cm.

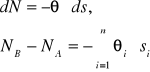
48. Objaśnij redukcję szerokości i długości astronomicznej na geoidę w rzeczywistym polu siły ciężkości. Wskaż te elementy redukcji, które dotyczą pola normalnego siły ciężkości.

Podstawowym składnikiem redukcji szerokości ' i długości ' zaobserwowanych metodami astronomicznymi są wzory uzyskane po przekształceniu wzoru na nachylenie powierzchni ekwipotencjalnej:

Po przekształceniach:

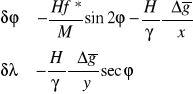
g - przeciętna wartość przyśpieszenia siły ciężkości wzdłuż linii pionu,

γ - przeciętna wartość przyśpieszenia normalnego.

Podstawowym problemem w powyższych wzorach jest wyznaczenie przeciętnej wartości przyspieszenia siły ciężkości (g) wzdłuż linii pionu.

Następne etapy redukcji wynikają ze wzorów na względne odchylenie linii pionu:

 _i^ag =  _i^a - B_i, i  _i ^ag = ( _i^a - L_i) cos  ^ag

Po przekształceniu otrzymamy:

δ B = - ^ag i δL = - ^ag

Wzory na szerokość geodezyjną B i długość geodezyjną L mają postać:

B = '+ δ + δB,

L = '+ δ + δL.

' i ' wielkości zaobserwowane na fizycznej powierzchni Ziemi

49. Jak można uwzględnić odchylenia pionu przy redukcjach długości linii na powierzchnię elipsoidy odniesienia?

Redukcja dł. S' pomierzonej na fizycznej powierzchni Ziemi i zredukowanej na średnią wysokość obu pkt. końcowych odcinka S' polega na wyznaczeniu różnicy pomiędzy:

• długością redukowaną bezpośrednio na elipsoidę S₀ (rzut normalny),

• długością S otrzymaną w wyniku najpierw pionowego rzutu na geoidę, a następnie normalnego rzutu z geoidy na elipsoidę odniesienia.

W pierwszym etapie korzystamy ze wzór na średnią wysokość: H_m = (1/2)(H_P + H_K + N_P + N_K).

Bezpośredni rzut ortogonalny S' na elipsoidę odniesienia wyrażamy wzorem:

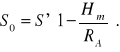
Gdy przyjmiemy, że powierzchnie geoidy i elipsoidy odniesienia są w granicach odcinka S nieznacznie nachylone to:

S - S₀ = _A/P H_P - _A/K H_K, gdzie:

_A/P, _A/K - rzut odchyleń pionu w pkt. P i K na płaszczyznę przekroju normalnego o azymucie A, w którym leży odcinek PK.

Rzut składowych odchyleń pionu na pł. wertykału:

_A/P = _PcosA + _PsinA

Przyjmujemy średnią wysokość:

H = (1/2)(H_P + H_K) to:

S - S₀ = H(_A/P - _A/K),

Redukcje dł. na pow. elipsoidy odniesienia w rzeczywistym polu siły ciężkości:

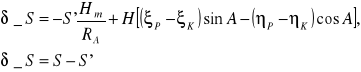
50. Przedstaw definicję wysokości normalnych Mołodeńskiego. Na czym polega różnica pomiędzy ścisłym i przybliżonym podejściem do wyznaczenia wartości wysokości normalnych?

Wysokość normalna Mołodeńskiego:

Wysokość geometryczna telluroidy (odległość telluroidy od elipsoidy)

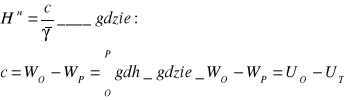
γ - przeciętna wartość przyspieszenia normalnego wzdłuż linii pionu pola normalnego s.c.

Podejścia do wyznaczenia wartości wys. norm.

• ścisłe:

Wyznaczamy wys. norm. poprzez proces iteracyjny wzorów:

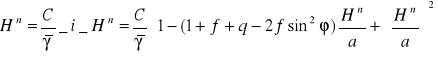
obliczenia rozpoczynamy dla Hⁿ = h.

• przybliżone:

W uproszczonym podejściu do wyznaczenia wys. norm. korzystamy ze wzorów:

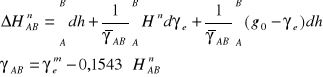
51. Przedstaw znane metody absolutnych pomiarów przyspieszenia siły ciężkości.

Pomiary absolutne (bezwzględne):

Uzyskujemy pełną wartość przyśpieszenia siły ciężkości (g) w miejscu obserwacji.

Do powyższych pomiarów stosujemy najczęściej metody `swobodnego spadku' i `podrzutu i spadku'. Polegają one na wyliczeniu przyspieszenia g na podstawie pomiarów długości drogi i czasu.

Metody absolutne:

• M. swobodnego spadku ciała:

Ciało pomiarowe jest puszczane z pewnej znanej

wysokości. Jednak precyzyjny pomiar drogi i interwału czasu nie jest możliwy w początkowym stadium lotu. Dlatego wielkości te mierzone są między co najmniej trzema punktami na torze spadającego ciała.

• M. podrzutu i spadku ciała:

Metoda ta jest nazywana `m. katapulty' lub `m. balistyczną', `m. symetryczną'. Za pomocą wyrzutni podrzucamy ciało materialne na pewną wysokość. Obserwujemy momenty jego przejścia przez co najmniej kilka pł. poziomych podczas wznoszenia i opadania. Mierzymy również odległości między tymi płaszczyznami.

52. Grawimetry statyczne: omów jeden ze znanych ci modeli grawimetru statycznego.

W instrumentach tych wykonujemy obserwacje stanu równowagi masy próbnej na którą działa siła ciężkości i siła ją kompensująca.

Firmy Texas Instruments produkuje grawimetr pod nazwą Worden. Wytwarzany jest on w 2 wersjach: geofizycznej (zakres ok. 180 mgal) i geodezyjnej (zakres ok. 5000 mgali). Wersja geodezyjna posiada jak gdyby 2 zakresy pomiarowe: duży zwany geodezyjnym i mały równy geofizycznemu. Natomiast w wersji geofizycznej zakres duży nie jest wyposażony w urządzenie odczytowe.

System mierzący w tych instrumentach wykonany jest z kwarcu i składa się z następujących elementów:

• sprężyny pomiarowej (głównej),

• sprężyny i śruby odczytu,

• sprężyny i śruby zmiany zakresu pomiarowego,

• dźwigni poziomej obciążonej masą,

• nici torsyjnej,

• wskaźnika położenia dźwigni,

• lunetki odczytowej,

• urządzenia kompensacji termicznej połączonego z górnym zaczepem sprężyny pomiarowej.

Grawimetry te są astatyzowane. Do pracy nie potrzebują zasilanie elektrycznego (oprócz systemu odczytowego). Systemy mierzące znajdują się w próżniowych zbiornikach, które dodatkowo znajdują się w szklanych naczyniach o podwójnych ściankach w celu dodatkowej ochrony termicznej.

Grawimetry te cechują się znacznymi dryftami:

• dryft długookresowy może przekroczyć 0,1 mgal/1godz.i jest dodatni,

• dryft krótkookresowy wynosi 0,05 mgal/1godz. I zmienia się z czaem starzenia się kwarcu.

53. Na czym polega cechowanie grawimetrów. Jakie znasz metody cechowania grawimetrów? Scharakteryzuj te metody pokrótce.

Powiązanie wskazań urządzenia odczytowego grawimetru z jednostką przyspieszenia siły ciężkości w wyniku czynności pomiarowych lub obliczeniowych. Otrzymane wartości liczbowe pozwalają na przeliczanie różnicy wskazań urządzenia odczytowego (liczby działek) na miligale.

Na bazach grawimetrycznych:

Metoda ta jest uniwersalna. Można kalibrować wszystkie grawimetry. Korzystamy z poligonu (z 2 pkt.) między którymi różnica przyspieszeń jest dokładnie wyznaczona. W celu zwiększenia dokładności korzystamy z większej liczby pkt. na bazach - wykonujemy pomiar na bazie, usuwamy z wyników pomiaru wpływ dryftu i wprowadzamy korektę ze względu na pływy skorupy ziemskiej. Następnie układamy układ równań Ei=an-g_bazy (n-odczyt grawimetru, g_bazy-różnica przyśpieszenia na bazie) i rozwiązujemy go metodą najmniejszych kwadratów. Uzyskamy niewiadomą (a) - współczynnik grawimetru. Dokładność szacowania tej metody jest na poziomie ±(1,0-3,0)*10^-4 (a). dokładność tej metody jest ograniczona przez transport (wstrząsy), wpływy termiczne i wpływy atmosfery.

Przez nachylenie (dla grawimetrów astatyzowanych): można stosować w laboratoriach wyposażonych w odpowiedni egzaminator, umożliwiający pomiar kąta wychylenia. Dzięki wychyleniu pozornie zmienia się przyspieszenie. Cechowanie polega na wykonaniu kilku serii pomiarów symetrycznych wychylając w lewo i wprawo o niewielkie kąty. Zalety: większa dokładność, stałe warunki termiczne, brak nieregularności dryftu.

Obciążenie dźwigni układu pomiarowego:

może być stosowana tylko w nielicznych typach grawimetrów nie hermetycznych mających wewnętrzny układ pomiarowy ze specjalną przystawką kalibrującą.

54. Opisz znane ci poprawki pomiarów grawimetrami.

Poprawki ze względu na dryft grawimetru.

Wyniki pomiarów z wprowadzonymi poprawkami luno-solarnymi, musimy poprawić ze względu na dryft systemu pomiarowego grawimetru. Odpowiednie poprawki z tego tytułu wyznacza się z reguły przy założeniu liniowych zmian dryftu, proporcjonalności dryftowych zmian wskazań grawimetru do czasu.

Poprawki te możemy obliczyć ze wzoru: PgσσTj, gdzie:

Tj - oznacza interwał czasu pomiędzy kolejnymi odczytami grawimetru na pkt. pomiarowych,

σ  (ny), n - różnica wskazań grawimetru kończącego i rozpoczynającego pomiaru i-tej stacji w mgal lub działkach.

Poprawki luno-solarne.

Poprawki spowodowane zmianami przyspieszenia siły ciężkości spowodowane przyciąganiem Księżyca i Słońca:

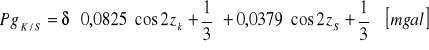
Podczas pomiarów grawimetrycznych należy notować średnie momenty odczytów z grawimetru na chronometrze powiązanym ze skalą czasową, zegarek z czasem lokalnym. można z nich wyliczyć lub odczytać z tablic astronomicznych odpowiednie wartości współrzędnych równikowych Księżyca i Słońca i policzyć kąt godzinny. Maksymalne poprawki ze względu na przyciąganie Księżyca mogą osiągać wartość 0,135 mgal, a Słońca 0,053 mgal. Łączna wartość poprawki luno-solarnej może dochodzić do 0,19 mgal.

55. Transformacja geodezyjna Helmerta-Hristowa: objaśnij metodę i kolejne etapy transformacji.

Metoda transformacji współrzędnych elipsoidalnych stosowana dla obszarów nie przekraczających kilku mln m² (powierzchnia o promieniu około 1000 km)

* Ogólne założenia:

B=B₀+b=B₀+f₁(B₀,s,A,a,f) \

L=L₀+l=L₀+f₂(B₀,s,A,a,f) ] (1)

b=B-B₀, l=L-L₀ /

B_o, L₀ - wsp. pkt. początkowego linii geod. s

B, L - wsp. pkt. końcowego linii geod. s

Zmiany dB₀, dL₀, ds, da, df powodują zmiany dB, dL, które wyrażają różnice zupełne funkcji (1) Helmerta. Hristow zróżniczkował wyrażenia B, L, A, względem B, s, a, f. Otrzymane pochodne wstawił do wzoru Helmerta.

dB_i= A'_idL₀+B'_idB₀+C'_idp+D'_idA

dL_i= A”_idL₀+B”_idB₀+C”_idp+D”_idA

Z tego układu oblicza się niewiadome dB₀, dL₀, dp, dA, met. najmniej. kwadratów, gdy liczba pkt łącznych > 2.

Dokładność transformacji ocenia się na podstawie rozbieżności współrzędnych pkt. łącznych przetransformowanych na siebie za pomocą wyznaczonych elementów transformacji. Punkty łączne powinny być równomiernie rozłożone na obszarze objętym transformacją.

56. Omów ogólne zasady transformacji współrzędnych geodezyjnych.

Transformacja współrzędnych geodezyjnych pomiędzy dwoma układami geodezyjnymi (pierwotnym i wtórnym) polega na obliczeniu wsp. w układzie wtórnym dla pkt., których wsp. znane są w układzie pierwotnym. Wykonujemy to na podstawie wsp. pkt. znanych w obu układach, zwanych pkt. łącznymi. Zbiór pkt. łącznych jest częścią wspólną zbiorów pkt. układu pierwotnego i wtórnego. Pkt. łączne mogą służyć do określenia tzw. modelu transf. (prawa transf.). Gdy model transf. jest znany w postaci ogólnych związków matematycznych pomiędzy wsp. w obu układach, to pkt. łączne stanowią tylko podstawę do wyznaczenia parametrów trans.

	Wsp. pkt. łącznych (ukł. pierw.)
	
Wsp. pkt. do s transformacji (ukł. pierw.)	Model → (prawo) → TRANSFORM.	Wsp. pkt. po s transformacji (ukł. wtórny.)
	
	Wsp. pkt. łącznych (ukł. wtórny)

57. Omów istotę oraz scharakteryzuj poszczególne etapy transformacji Helmerta-Hristowa.

Metoda transformacji współrzędnych elipsoidalnych stosowana dla obszarów nie przekraczających kilku mln m² (powierzchnia o promieniu około 1000 km)

* Ogólne założenia:

B=B₀+b=B₀+f₁(B₀,s,A,a,f) \

L=L₀+l=L₀+f₂(B₀,s,A,a,f) ] (1)

b=B-B₀, l=L-L₀ /

B_o, L₀ - wsp. pkt. początkowego linii geod. s

B, L - wsp. pkt. końcowego linii geod. s

Zmiany dB₀, dL₀, ds, da, df powodują zmiany dB, dL, które wyrażają różnice zupełne funkcji (1) Helmerta. Hristow zróżniczkował wyrażenia B, L, A, względem B, s, a, f. Otrzymane pochodne wstawił do wzoru Helmerta.

dB_i= A'_idL₀+B'_idB₀+C'_idp+D'_idA

dL_i= A”_idL₀+B”_idB₀+C”_idp+D”_idA

Z tego układu oblicza się niewiadome dB₀, dL₀, dp, dA, met. najmniej. kwadratów, gdy liczba pkt łącznych > 2.

Dokładność transformacji ocenia się na podstawie rozbieżności współrzędnych pkt. łącznych przetransformowanych na siebie za pomocą wyznaczonych elementów transformacji. Punkty łączne powinny być równomiernie rozłożone na obszarze objętym transformacją.

58. Omów transformację afiniczną współrzędnych x, y, z; przedstaw zawężenie modelu transformacji do jednego współczynnika skali (transformacja 7-parametrowa).

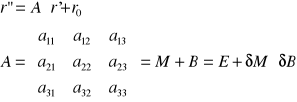
r” - wektor w układzie wtórnym,

r' - wektor w układzie pierwotnym,

r₀ - wektor translacji,

A - macierz obrotów i zniekształceń.

Trans. Quazi-afiniczna:

Założenie: δB*δM  δB+δM,

δM = diag(_x, _y, _z) - zniek. skali wzdłuż osi x, y, z.

A = δB+δM (B - m. Obrotu, M - m. zniekształceń)

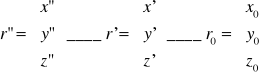
δ  (macierz obrotów eulerowskich γ, , 

Ostatecznie: r”=r'+r₀+(δB+δM)*r'

Parametry transformacji (_x, _y, _z, , , x₀, y₀, z₀)

7-o parametrowa transformacja to transformacja Bursy-Wolfa przez podobieństwo. Model takiej transformacji składa się z 3 macierzy obrotów elementarnych R_Z R_X R_Y. Iloczyn tych macierzy daje macierz obrotów R(,,γ) = R_Z R_X R_Y. Linearyzacja macierzy obrotów przez warunek ortogonalności macierzy (w wyniku linearyzacji otrzymujemy podobną macierz). Dzięki temu otrzymamy liniową macierz obrotów. Transformację przez podobieństwo zmodyfikował Mołodeński wprowadzając przesunięcie środka obrotów do pkt. środka sieci układu wtórnego co ma zapobiec wadom transformacji gdy jej obszar jest niewielki.

59. Redukcja współrzędnych x, y, z, na elipsoidę metodą rzutowania Helmerta i w rzeczywistym polu siły ciężkości; jakie przesłanki powinny decydować o wyborze metody redukcji.

Metoda rzutowania Helmerta:

Dzięki niej możemy przeliczyć współrzędne prostokątne (x,y,z) na współrzędne geodezyjne (B,L,H).

Używamy do tego wzorów: x=(N+H)cosBcosL, y=(N+H)cosBsinL, z=(^-1N+H)sinB, gdzie: ^-1=1-e².

p= pierw(x²+y²) = (N+H)cosB, H=(p/cosB)-N.

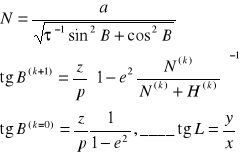
Met. Helmerta nie zależy od pola siły ciężkości dzięki czemu istnieje możliwość pełnego odwracania zależności (x,y,z) - (B,L,H) i (B,L,H) - (x,y,z).

Metoda Pizzettiego: Jest to redukcja w rzeczywistym polu S.C.

Znane: H^ort, , , gradient horyzontalny anomalii grawimetrycznych.

Kierunek zenitu astronomicznego określają  i , uzyskane z bezpośrednich obs. astr. δ,δ - redukcja kierunku na geoidę. Połowa redukcji  i , wyraża składowe kąta (1/2), czyli redukcję kierunku zenitu ( i  na kierunek cięciwy krzywej linii pionu. Gradient horyzontu koryguje założenie kołowego kierunku linii pionu.

Redukcja z F.P.Z. na geoidę:

^m+δ, ^m+δ, r^g=r-H^ortu

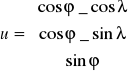
Pkt. (x^g, y^g, z^g) po zredukowaniu na geoidę rzutujemy na elipsoidę odniesienia za pomocą procedury Helmerta zastępując H przez N^g.

Reduk. Pizzettiego nie jest odwracalna.

O wyborze metody decyduje:

• analiza zniekształceń wynikających z redukcji wyników pomiarów GPS na pow. Elipsoidy,

• należy unikać stosowania różnych metod redukcji w jednej sieci.

• Podaj definicje niwelacji satelitarnej; omów zasadnicze podejście do niwelacji satelitarnej w skali globalnej i regionalnej.

Niwelacją satelitarną nazywamy procedurę prowadzącą do uzyskania wysokości ortometrycznych na podstawie wysokości geometrycznych, wyzn. techniką GPS.

H^ort = H - N, H^ort = (W_O-W_P)/g

Wysokości ortometryczne (H^ort) są to długości odcinków linii pionu rzeczywistego pola siły ciężkości mierzone od powierzchni geoidy do fiz. pow. Ziemi. Wynika z tego że różnica pomiędzy wysokościami geom. i ortome. tkwi w N (odstępie geoidy od elipsoidy).

Wysokości geometryczne (H) są to odległości mierzone od powierzchni elipsoidy geocentrycznej do pkt. na fizycznej pow. Ziemi.

Skala globalna:

Długookresowe zmiany geoidy (okres ponad 100 km po przeliczeniu na jednostki liniowe). Wartość tych zmian osiąga pojedyncze metry. Obliczamy je na podstawie mapy pola grawitacyjnego Ziemii.

Skala regionalna:

Średniookresowe zmiany geoidy (okresy ponad 20 km po przeliczeniu na jednostki liniowe). Wartość tych zmian osiąga pojedyncze decymetry. Obliczamy je na podstawie modelu pola grawitacyjnego i anomalii grawimetrycznych uzyskanych z pomiarów terenowych w trapezach sferycznych np. 20'x20'.

Skala lokalna:

Krótkookresowe zmiany geoidy. Wyznaczamy je na podstawie lokalnych, szczegółowych anomalii grawimetrycznych w trapezach o bokach mniejszych od kilku minut stopniowych (< od 20 km). Wymagają one uwzględnienia redukcji topograficznych i zróżnicowanego podejścia w zależności od charakteru terenu (problem obszarów górskich).

61. Omów zasadnicze podejście do niwelacji satelitarnej na małych obszarach.

-Interpolacja odstępów geoidy od elipsoidy:

jeżeli na obszarze objętym siecią punktów GPS znajdują się punkty o znanych wysokościach ortometrycznych, lub zostały dowiązane wysokościowo do pkt. znanych w systemie wysokości ortometrycznych, to można wyznaczyć przybliżony przebieg geoidy na tym obszarze za pomocą procedury interpolacyjnej (obszar 10 x 10 km).

-wykorzystanie niwel. astro. i pomiarów GPS:

Nachylenie geoidy (metoda niwelacji astronomicznej), także różnice jej odstępów w sąsiednich pkt. GPS, jeżeli wyznaczone zostały składowe odchylenia pionu z obs. astronomicznych. Współrzędne (,) redukuje się na geoidę, oblicza składowe odchyleń pionu B (L)cos. W celu wyznaczenia odstępu geoidy od elipsoidy, dokonuje się interpolacji N. Przynajmniej 1 pkt. GPS powinien posiadać wysokość ortometryczną.

-wykorzystanie niwel. trygono. i pomiarów GPS:

Na podstawie względnych obs. GPS dowiązanych do znanej pozycji w ukł. WGS-84 i niw. trygonom. można wyznaczyć N wzdłuż ciągu trygonom. Od pomiarów GPS należy wymagać, aby H pkt odległych o ok. 350 m charakteryzowała się bł. śr. nie przekraczającym 2 mm.

Dla 1-o km ciągu niwel. tryg. N wyznaczymy z błędem ponad 4 mm.

Niwel. sat. o takiej dokładności mogła by sprostać wymaganiom w zakresie inżynierii budowlanej: projektom wodnym, budowie autostrad i kolei (takie dokł. są obecnie trudne do osiągnięcia).

---