 | Pobierz cały dokument egzamin.sciagi.gik.semestr.3.geodezja.wyzsza.do.doc Rozmiar 428 KB |
Układ współrzędnych naturalnych; uzasadnij, że trójka liczb P, P, WP jednoznacznie określa położenie punktu P w przestrzeni względem naturalnego układu współrzędnych.
Układ wsp. naturalnych: związek układu horyzontalnego, będącego lokalnym układem obserwacyjnym na powierzchni Ziemi (taki w którym dokonano obserwacji), z układem globalnym.
* podstawowa oś układu to chwilowa oś obrotu ziemi ( ω ) przechodząca przez pkt. S środka mas ziemi
* płaszczyzna poprowadzona przez pkt. S i jednocześnie prostopadła do chwilowej osi obrotu ziemi to płaszczyzna równika astronomicznego.
* w obserwatorium astronomicznym Greenwich poprowadzono pęk płaszczyzn wertykalnych, zawierających kierunek linii pionu w tymże obserwatorium. Z tego pęku płaszczyzn wybrano tą która jest równoległa do osi wirowania ziemi ϖ i nazwano ją płaszczyzną południka astronomicznego Greenwich.
p -szer. gegraf.-astronom kąt zawarty między pł. równika, a kierunkiem linii pionu pkt. P.
λp -dł. gegraf.-astronom kąt zawarty między pł. południka Greenwich, a pł. południka pkt. P.
Wp -wartość potencjału powierzchni w danym pkt. P
P(ϕ, λ, Wp) ϕ (0°, 90°) λ(0°,360° lub 180° ). Dodatkowo musi być znana chwilowa oś obrotu Ziemi oraz pł. południka zerowego.
Uzasadnij, że pomiędzy głównymi promieniami krzywizny elipsoidy obrotowej zachodzi następująca zależność M=N(1-e2)/W2.
Promień krzywizny południka M wynosi M=(ds./dB).
Wzór ten możemy przekształcić do postaci:
![]()
Różniczkę (dp/dB) wyznaczymy ze wzoru:
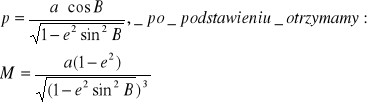
Wyrażenie na promień równoleżnika (p) daje podstawę do wyznaczenia promienia krzywizny w I wertykale. Jeśli skorzystamy z tw. Meusniera (promień krzywizny przekroju ukośnego, mającego wspólną styczną z przekrojem normalnym, może być wyrażony przez zrzutowanie promienia krzywizny przekroju normalnego na kierunek promienia przekroju ukośnego). Wobec tego mamy:
![]()
Powtarzające się wzory w mianownikach na M i N, gdzie M=<N oznaczamy przez:
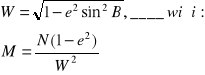
Pokaż, że średni promień krzywizny elipsoidy obrotowej jest średnią geometryczną głównych promieni krzywizny.
Prowadząc pęk płaszczyzn przez normalną w dowolnym pkt. na elipsoidzie obrotowej, otrzymamy przekroje normalne elipsoidy. W każdym pkt. powierzchni istnieją takie dwa wzajemnie prostopadłe przekroje normalne, których krzywe charakteryzuję się ekstremalnymi krzywiznami. Nazywa się je przekrojami w kierunkach głównych. Na elipsoidzie obrotowej (z wyjątkiem jej biegunów) jest to kierunek południka geodezyjnego (krzywizna max M-1) oraz wertykału prostopadłego do południka, zwanego pierwszym wertykałem (krzywizna N-1).
 | Pobierz cały dokument egzamin.sciagi.gik.semestr.3.geodezja.wyzsza.do.doc rozmiar 428 KB |