ŻEBRO.
Zestawienie obciążeń.
L.p |
Wyszczególnienie i obliczenie wartości |
Obc. char. |
Wsp. Obc. |
Obc. obl. |
|||
|
|
|
|
|
|
||
1. |
Obciążenie stałe z płyty 2,65x2,0 |
5,3 kN/m |
|
6,12 kN/m |
- |
||
|
|
|
|
- |
4,62 kN/m |
||
2. |
ciężar własny żebra 0,20x0,37x24,0 |
1,78 kN/m |
1,1 (0,9) |
1,96 kN/m |
1,60 kN/m |
||
Obciążenie stałe |
|||||||
Obciążenie zmienne |
1,2 |
|
|||||
Aby móc skorzystać z tablic Winklera trzeba obciążenia określić następująco:
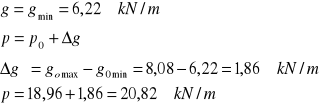
3.2. Schemat statyczny.
Zakładając oparcie żeber na szerokości wieńca równej 0,25 m.
l1=6,0+0,25/2=6,125 m.
Rzędne obwiedni momentów zginających i sił tnących obliczone z tablic Winklera.
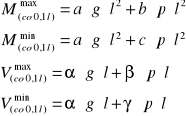
Przykładowe obliczenia dla przęsła skrajnego (x/l=0,1):
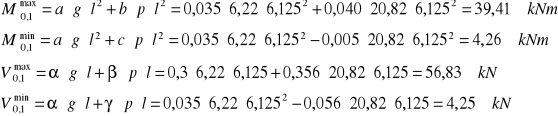
Przykładowe obliczenia dla przęsła środkowego (x/l=0,1):

Zestawienie Mmax, Mmin ,Vmax ,Vmin.
x/l |
l |
a |
b |
c |
|
|
γ |
Mmax |
Mmin |
Vmax |
Vmin |
|
|
|
PRZĘSŁO SKRAJNE |
|
|
|
|
|
|||
0 |
0,000 |
0,000 |
0,000 |
0,000 |
0,4 |
0,450 |
-0,050 |
0,00 |
0,00 |
72,62 |
8,86 |
0,1 |
0,613 |
0,035 |
0,040 |
-0,005 |
0,3 |
0,356 |
-0,056 |
39,41 |
4,26 |
56,83 |
4,25 |
0,2 |
1,225 |
0,060 |
0,070 |
-0,010 |
0,2 |
0,275 |
-0,075 |
68,68 |
6,19 |
42,71 |
-1,97 |
0,3 |
1,838 |
0,075 |
0,090 |
-0,015 |
0,1 |
0,207 |
-0,107 |
87,80 |
5,78 |
30,14 |
-9,77 |
0,4 |
2,450 |
0,080 |
0,100 |
-0,020 |
0,0 |
0,150 |
-0,150 |
96,78 |
3,05 |
19,08 |
-19,08 |
0,5 |
3,063 |
0,075 |
0,100 |
-0,025 |
-0,1 |
0,104 |
-0,204 |
95,61 |
-2,03 |
9,48 |
-29,85 |
0,6 |
3,675 |
0,060 |
0,090 |
-0,030 |
-0,2 |
0,069 |
-0,269 |
84,30 |
-9,43 |
1,23 |
-41,97 |
0,7 |
4,288 |
0,035 |
0,070 |
-0,035 |
-0,3 |
0,044 |
-0,344 |
62,84 |
-19,17 |
-5,78 |
-55,34 |
0,8 |
4,900 |
0,000 |
0,040 |
-0,040 |
-0,4 |
0,028 |
-0,428 |
31,41 |
-31,41 |
-11,67 |
-69,82 |
0,85 |
5,206 |
-0,021 |
0,028 |
-0,049 |
|
|
|
16,70 |
-43,22 |
0,00 |
0,00 |
0,9 |
5,513 |
-0,045 |
0,020 |
-0,065 |
-0,5 |
0,019 |
-0,519 |
5,45 |
-61,60 |
-16,59 |
-85,25 |
0,95 |
5,819 |
-0,071 |
0,017 |
-0,088 |
|
|
|
-3,29 |
-85,60 |
0,00 |
0,00 |
1 |
6,125 |
-0,100 |
0,017 |
-0,117 |
-0,6 |
0,017 |
-0,617 |
-10,31 |
-114,46 |
-20,73 |
-101,50 |
|
|
|
PRZĘSŁO ŚRODKOWE |
|
|
|
|
|
|
|
|
0 |
6,125 |
-0,100 |
0,017 |
-0,117 |
0,5 |
0,583 |
-0,083 |
-13,47 |
-149,50 |
106,78 |
9,63 |
0,1 |
6,825 |
-0,055 |
0,015 |
-0,070 |
0,4 |
0,487 |
-0,087 |
-1,32 |
-88,32 |
88,39 |
4,74 |
0,2 |
7,525 |
-0,020 |
0,030 |
-0,050 |
0,3 |
0,399 |
-0,099 |
24,51 |
-57,10 |
71,23 |
-1,38 |
0,3 |
8,225 |
0,005 |
0,055 |
-0,050 |
0,2 |
0,321 |
-0,121 |
57,63 |
-49,49 |
55,49 |
-8,93 |
0,4 |
8,925 |
0,020 |
0,070 |
-0,050 |
0,1 |
0,254 |
-0,154 |
77,51 |
-44,91 |
41,33 |
-18,05 |
0,5 |
9,625 |
0,025 |
0,075 |
-0,050 |
0,0 |
0,198 |
-0,198 |
84,13 |
-43,39 |
28,84 |
-28,84 |
OBWIEDNIA MOMENTÓW ZGINAJĄCYCH - wartości w [kNm]
OBWIEDNIA SIŁ TNĄCYCH - wartości w [kN]
Wymiarowanie żebra.
Szerokość płyty współpracująca z żebrem.
a1= 2 cm+ 1 cm=3 cm
d= h - a1-∅/2=45-2-2/2= 42 cm
![]()
![]()
Przyjęcie klasy betonu i stali.
przyjęto beton B25 - fcd =13,3 MPa =13300 kPa
stal AII 18G2 - fyd=310 MPa = 310000 kPa
Sprawdzenie „teowości” belki.
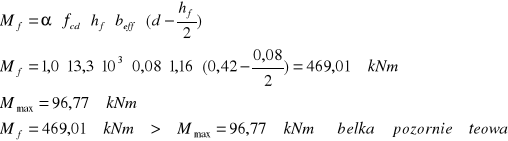
Wymiary belki : beff x d=1,16 x 0,42 m.
Obliczenie zbrojenia na zginanie.
przęsło A-B (C-D)

PRZYJĘTO 5∅14 o Fa=7,70 cm2
przęsło B-C

PRZYJĘTO 5∅14o Fa=7,70 cm2
Zbrojenie na momenty podporowe:
nad przęsłem B
bw x d = 0,20 x 0,42

PRZYJĘTO 8∅14 o Fa=12,32 cm2
zbrojenie na zastępczy moment ujemny w przęśle B-C:
![]()

PRZYJĘTO 5∅14 o Fa=7,70 cm2
Obliczenie zbrojenia na ścinanie.
przy podporze A : siła tnąca przy licu ściany - VSd=70,68 kN
- siła przenoszona przez beton:
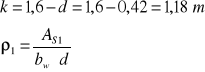
Ponieważ przy podporze A zakładam odgięcie 2 prętów , więc AS1=3∅14=4,62 cm2
![]()
![]()
-odcinek na którym niezbędne są strzemiona:

Zakładam że strzemiona przeniosą 50% VSd=70,68/2=35,34 kN
Przyjęto strzemiona cztero-cięte ∅6 ![]()
Rozstaw strzemion: (ctgΘ =c1/z ,c1-długość jednostkowego odcinka zbrojonego strzemionami i prętami odgiętymi jest równa c1=z+0,05 m.=0,378+0,05=0,428 m.,
ctgΘ=0,428/0,378=1,13
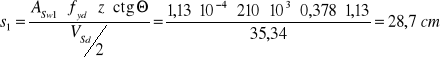
Maksymalny rozstaw strzemion smax w kierunku podłużnym określają następujące warunki:
- jeśli ![]()
jeśli

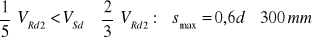
- jeśli ![]()
W naszym przypadku 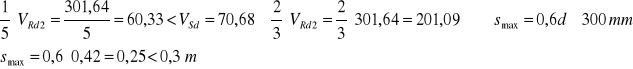
przyjęto s1=25 cm
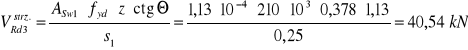
-odcinek na którym niezbędne są pręty odgięte:
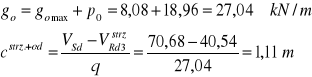
Więc odcinek c dzielę na trzy odcinki zbrojone strzemionami i jednym prętem odgiętym (c1=c2=c3=42 cm) , ![]()
![]()
. (Cały odcinek ścinania będzie zazbrojony strzemionami i prętami odgiętymi.)
UWAGA : Ponieważ na odcinku c1, gdzie występuje największa siła ścinająca można zastosować strzemiona co 25 cm, więc na odcinkach c2 i c3 gdzie występuje mniejsza siła ścinająca przyjmuję też taki sam rozstaw strzemion , należy jeszcze sprawdzić czy połowę maksymalnej siły ścinającej przeniesie jeden pręt odgięty (zakładam w każdym odcinku jeden pręt odgięty ∅ 14 mm).
Obliczam siłę jaką przeniesie jeden pręt odgięty ∅ 14 mm.
ASw2=1,54 cm2, stal AII 18G2 - fyd=310 MPa = 310000 kPa, s2=0,42 m.
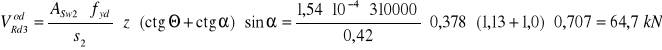
Zakładam że pręty odgięte przeniosą 50% VSd=70,68/2=35,34kN<![]()
,
więc warunek został spełniony.
Obliczam maksymalną siłę poprzeczną jaką mogą przenieść pręty odgięte i strzemiona.
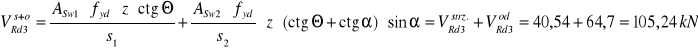
VSd=70,68<![]()
WNIOSEK : Na całym odcinku ścinania przyjmuje strzemiona ∅ 6 mm cztero cięte w rozstawie co 25 cm, oraz cały odcinek ścinania jest podzielony na trzy mniejsze w których , w każdym znajduje się jeden pręt odgięty ∅ 14 mm. (Na odcinku c1 i c2 będą pręty odgięte z przęsła, a na odcinku c3 będzie zastosowana dodatkowa nakładka)
Ścinanie przy podporze B : siła tnąca przy licu podciągu - VSd=103,41 kN
UWAGA: Ponieważ wielkości sił tnących po obu stronach podpory B są zbliżone to zbrojenie po lewej i prawej stronie przyjmuje jako takie same.
- siła przenoszona przez beton:
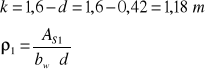
Ponieważ przy podporze A zakładam odgięcie 3 pręta , więc AS1=2∅14=3,08 cm2
![]()
Ponieważ pręty nad podporą B będą umieszczone w dwóch rzędach, a pomiędzy nimi musimy zapewnić przestrzeń nie mniejszą niż 30 mm, więc d=0,42-0,03=0,39 m.
-odcinek na którym niezbędne są strzemiona:
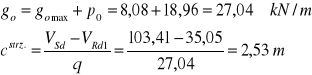
Zakładam że strzemiona przeniosą 50% VSd=103,41/2=51,71 kN
Przyjęto strzemiona cztero-cięte ∅6 ![]()
Rozstaw strzemion:
(ctgΘ =c1/z ,c1-długość jednostkowego odcinka zbrojonego strzemionami i prętami odgiętymi jest równa c1=z+0,05 m.=0,35+0,05=0,40 m.,
ctgΘ=0,40/0,35=1,14
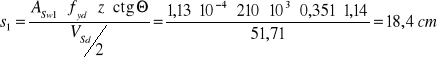
Maksymalny rozstaw strzemion smax w kierunku podłużnym określają następujące warunki:
- jeśli ![]()
jeśli

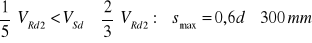
- jeśli ![]()
W naszym przypadku 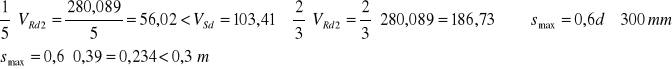
przyjęto s1=18 cm
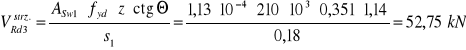
-odcinek na którym niezbędne są pręty odgięte:
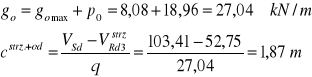
Więc odcinek c dzielę na pięć odcinków zbrojonych strzemionami i jednym prętem odgiętym (c1=c2=c3=c4=c5=40 cm) , ![]()
![]()
.
UWAGA : Ponieważ na odcinku c1, gdzie występuje największa siła ścinająca można zastosować strzemiona co 18 cm, więc na odcinkach c2 , c3, c4, c5, gdzie występuje mniejsza siła ścinająca przyjmuję też taki sam rozstaw strzemion , należy jeszcze sprawdzić czy połowę maksymalnej siły ścinającej przeniesie jeden pręt odgięty (zakładam w każdym odcinku jeden pręt odgięty ∅ 14 mm).
Obliczam siłę jaką przeniesie jeden pręt odgięty ∅ 14 mm.
ASw2=1,54 cm2, stal AII 18G2 - fyd=310 MPa = 310000 kPa, s2=0,40 m.
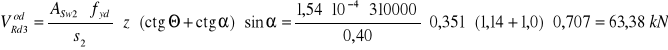
Zakładam że pręty odgięte przeniosą 50% VSd=103,4/2=51,7kN<![]()
,
więc warunek został spełniony.
Obliczam maksymalną siłę poprzeczną jaką mogą przenieść pręty odgięte i strzemiona.
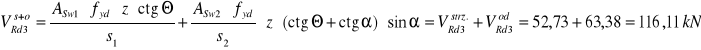
VSd=103,41 kN<![]()
WNIOSEK : Na odcinku ścinania równym 2m przyjmuje strzemiona ∅ 6 mm cztero cięte w rozstawie co 18 cm, oraz odcinek ten jest podzielony na pięć 40 cm w których , w każdym znajduje się jeden pręt odgięty ∅ 14 mm.
-Rozstaw strzemion na odcinku oddalonym od lica podpory o 2 m, do końca odcinka ścinania, czyli do punktu oddalonego od lica podpory o, VSd=69,31 kN : ![]()
odcinek c6=2,53-2,0=0,53 m.
ctgΘ = c6/z =0,53/0,351=1,51 1< ctgΘ = 1,51<2
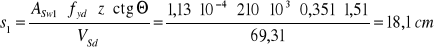
Maksymalny rozstaw strzemion smax w kierunku podłużnym określają następujące warunki:
- jeśli ![]()
jeśli

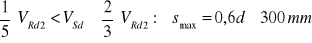
- jeśli ![]()
W naszym przypadku 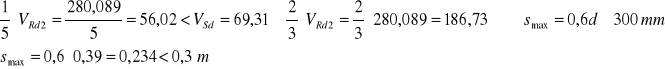
przyjęto rozstaw strzemion s1=18 cm
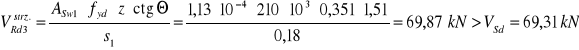
Obliczenia nośności prętów.
przykładowe obliczenia dla przęseł (dla jednego pręta) :
![]()
przykładowe obliczenia nad podporami (dla jednego pręta) :
![]()
ZESTAWIENIE OBLICZEŃ
OBLICZENIE OBWIEDNI NOŚNOŚCI DLA PRZĘSEŁ |
|
|
|
|
|
Ilość prętów |
Fa [cm] |
|
d [m.] |
fyd [kPa] |
M. [kNm] |
1 |
1,54 |
0,98 |
0,42 |
310000 |
19,65 |
2 |
3,08 |
0,98 |
0,42 |
310000 |
39,30 |
3 |
4,62 |
0,98 |
0,42 |
310000 |
58,95 |
4 |
6,16 |
0,98 |
0,42 |
310000 |
78,60 |
5 |
7,7 |
0,98 |
0,42 |
310000 |
98,25 |
OBLICZENIE OBWIEDNI NOŚNOŚCI NAD PODPORAMI |
|
|
|
|
|
Ilość prętów |
Fa [cm] |
|
d [m.] |
fyd [kPa] |
M. [kNm] |
1 |
1,54 |
0,835 |
0,42 |
310000 |
16,74 |
2 |
3,08 |
0,835 |
0,42 |
310000 |
33,48 |
3 |
4,62 |
0,835 |
0,42 |
310000 |
50,23 |
4 |
6,16 |
0,835 |
0,42 |
310000 |
66,97 |
5 |
7,7 |
0,835 |
0,42 |
310000 |
83,71 |
6 |
9,24 |
0,835 |
0,42 |
310000 |
100,45 |
7 |
10,78 |
0,835 |
0,42 |
310000 |
117,20 |
8 |
12,32 |
0,835 |
0,42 |
310000 |
133,94 |
g=6,22 kN/m
![]()
![]()
![]()
![]()
![]()
p=20,82 kN/m
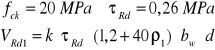
![]()
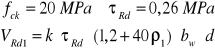
![]()
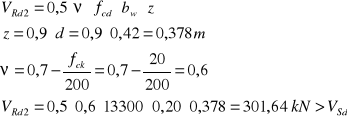
![]()
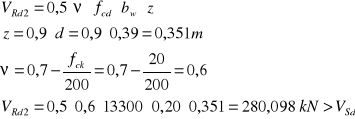
Wyszukiwarka