POLITECHNIKA SZCZECIŃSKA
PROJEKT DOMKU JEDNORODZINNEGO W TECHNOLOGII TRADYCYJNEJ
Sporządził:
Kasprowiak Łukasz
Rok II
Grupa 4
S P I S T R E Ś C I
I CZĘŚĆ TEKSTOWA
Opis techniczny
II RYSUNKI
Rys. 1 Rzut fundamentów 1:50
Rys. 2 Rzut parteru 1:50
Rys. 3 Układ belek stropowych nad parterem 1:50
Rys. 4 Rzut poddasza 1:50
Rys. 5 Rzut więźby dachowej 1:50
Rys. 6 Rzut dachu 1:50
Rys. 7 Przekrój pionowy A-A 1:50
Rys. 8 Szczegół konstrukcyjny :”A” 1:50
O P I S T E C H N I C Z N Y
1.Dane ogólne:
- Przeznaczenie budynku:
Projektowany obiekt jest przewidziany jako budynek mieszkalny, jednorodzinny.
- Powierzchnia użytkowa:
Parter
1. Wiatrołap 4,84 m˛
2. Hall 7,71 m˛
3. Pokój 14,98 m˛
4. Garderoba 2,53 m˛
5. Pokój 31,61 m˛
6. Kuchnia 14,93 m˛
7. Wc 2,2 m˛
8. Pom.gospodarcze+C.O. 10,5 m2
9. Garaż 23,64 m2
Razem 112,93 m²
Poddasze
1. Hall 3,64 m²
2. Pokój 19,3 m²
3. Pokój 14,41 m²
4. Pokój 21,48 m²
5. Łazienka 19,85 m²
Razem 78,68 m²
Powierzchnia użytkowa 191,61 m²
Powierzchnia zabudowy 154,25 m²
Kubatura 393,4 m³
- Fundamenty:
Obciążenia od budynku na grunt są przekazywane przez ławy fundamentowe betonowe o szerokości 61cm i wysokości 40 cm. Na górnej warstwie fundamentu wykonana jest izolacja przeciwwilgociowa z 2 warstw papy izolacyjnej na lepiku. Głębokość posadowienia- 1,32m poniżej poziomu zerowego.
- Ściany zewnętrzne:
Warstwa nośna wykonana z cegły pełnej grubości 25cm, na zaprawie cementowej o grubości 1 cm. Warstwa termoizolacyjna wykonana z wełny mineralnej o grubości 12cm. Warstwę dociskową stanowi cegła pałna grubości 12cm. Warstwę zewnętrzną stanowi tynk cementowy o grubości 0,5 cm na siatce z polipropylenu.
- Ściany wewnętrzne nośne:
Wykonane z cegły pełnej grubość 25 cm na zaprawie cementowej o grubości 1 cm.
- Ściany wewnętrzne działowe:
Wykonane z cegły dziurawki grubość 12 cm na zaprawie cementowej o grubości 1 cm.
Komin:
Wykonany z cegły pełnej. Klasy 15. Łącznie 6 przewodów w tym:
4 przewody wentylacyjne, 1 przewód spalinowy i 1 dymowy.
Stropy:
Stropy gęsto żebrowe DZ- 3. Długości modularne 6,0 m, układ belek co 60 cm. Wysokość konstrukcyjna stropu h=23 cm
Dach:
Dach o konstrukcji płatwiowo-kleszczowej. Do konstrukcji zastosowano drewno klasy K27. Jako izolację przeciwwilgociową zastosowano paroizolację z folii PCV przybijaną do krokwi. Izolację termiczną stanowi warstwa wełny mineralnej grubości 130 mm układana między krokwiami. Pokrycie dachowe z blacho-dachówki:
Krokwie 6x20 cm
Kleszcze 6x16 cm
Płatew 14x24 cm
Słup 14x14 cm
Miecz 10x10 cm
Murłata 14x14 cm
Belka przyokienna 8x16 cm
Krokiew (2) 6x16 cm
Nadproża:
Nadproża żelbetowe prefabrykowane typu L19
Schody wewnętrzne:
Schody zostały wykonane jako schody drewniane. Balustrady drewniane wsparte na słupkach. Dwa biegi po 8 stopni na bieg. S = 28 cm. H=17,7cm Przyjęto szerokość spocznika 80cm, długość 185 cm. Szerokość biegu wynosi 82,5 cm. Schody zewnętrzne: Schody zostały wykonane jako schody żelbetowe. Wykończenie stopni - płytki ceramiczne, anty poślizgowe o podwyższonej wytrzymałości.
Podłoga na parterze:
Podkład: 8 cm styropian, następnie 4 cm wylewki cementowej
Wykończenie:
-płytki ceramiczne
-panele podłogowe
Drzwi:
Drzwi wejściowe do budynku o szerokości 80 cm w świetle ościeżnicy, wykonane z drewna dębowego, lakierowane. Drzwi do pokoi o szerokości 80 cm w świetle ościeżnicy, wykonane z drewna. Drzwi do łazienki, WC o szerokości 80 cm w świetle ościeżnicy z kratkami nawiewnymi na dole, wykonane z drewna. Drzwi do pomieszczenia gospodarczego o szerokości 80 cm, wykonane z drewna.
Okna:
Wszystkie okna wykonano z drewna.
Roboty blacharskie:
Obróbki blacharskie wykonane są z blachy ocynkowanej, powlekanej poliestrami. Rynny i rury spustowe wykonane są z nieplastyfikowanego polichlorku winylu .
rynny = 10
b) rury spustowe = 7
Podokienniki wykonane są z blachy ocynkowanej powlekanej poliestrami.
Izolacje:
Ławy fundamentowe i ściany zagłębione w gruncie zostały zaizolowane podwójną warstwą papy na lepiku. Izolacja została wyprowadzona do poziomu podłogi na gruncie. Paroizolacja pionowa ścian zewnętrznych folia PCV. Ściany ocieplone wełną mineralną o grubości 120 mm ( zewnętrzne).W podłodze parteru zastosowano styropian grubości 90 mm pomiędzy krokwiami wełna mineralna grubości 130 mm.
Wyposażenie budynku:
Instalacja wodociągowa (wg osobnego projektu)
Ciepła woda użytkowa (wg osobnego projektu)
Kanalizacja sanitarna (wg osobnego projektu)
Kanalizacja deszczowa
Instalacja grzewcza: centralne
Instalacja gazowa (wg osobnego projektu)
Wentylacja: grawitacyjna
Instalacja elektryczna (wg osobnego projektu)
Ochrona od porażeń
Instalacja odgromowa (wg osobnego projektu)
Obliczenia
OBLICZENIE DACHU:
Budynek o wymiarach w rzucie, w świetle murów B = 11,41 m, L = 8,45 m, i wysokości H = 4,03 m zlokalizowany w I strefie obciążenia wiatrem i I strefie obciążenia śniegiem.
Wiązar ma być wykonany z drewna sosnowego klasy C-30
Pokrycie - blacho-dachówką.
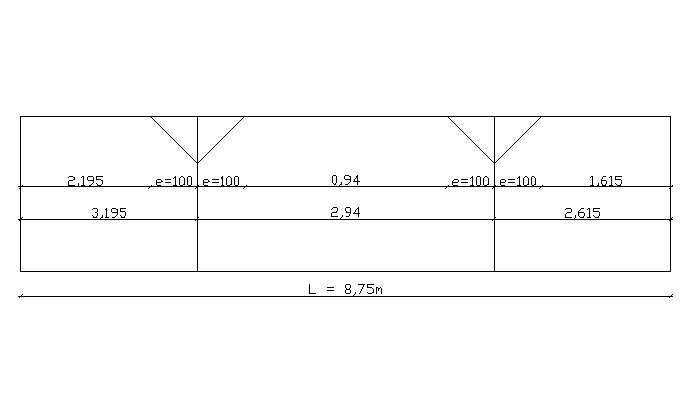
Rozstaw krokwi a = 1,14 m, pochylenie połaci dachowej α=22o, rozstawy wiązarów pełnych l1= 2,615 m, l2= 2,94 m, l3= 3,195 m, wysięg mieczy e= 1,00 m.
Drewno klasy C-30
Wytrzymałość charakterystyczna na zginanie fm,k=30 N/mm2 (Mpa)
Wytrzymałość charakterystyczna na ściskanie wzdłuż włókien fc,0,k= 23 N/mm2
Wytrzymałość charakterystyczna na ściskanie w poprzek włókien fc,90,k= 5,7 N/mm2
Współczynniki obciążenia ( częściowe współczynniki bezpieczeństwa) - γf
Ciężar własny konstrukcji drewnianej γf = 1,1
Ciężar własny pokrycia dachowego γf = 1,2
Obciążenie śniegiem γf = 1,4
Obciążenie wiatrem γf = 1,3
WIELKOŚCI GEOMETRYCZNE UZUPEŁNIAJĄCE
α=22O
sin α = 0,3746
cosα = 0,9272
tgα = 0,4040
Rozpiętość obliczeniowa wiązara l0 = 11,66 cm
Wysokość wiązara h0 = 0,5∗ l0 ∗ tgα = 0,5∗11,66∗ tgα = 2,355 m
Długość krokwi l = l0 / 2 cosα = 11,66/2cosα = 6,287 m
(zakładamy podział krokwi na część dolną i górną w stosunku v= ld / l![]()
0,6)
ld =![]()
= 4,37 m < 4,5 m ![]()
lg =![]()
= 1,98 m < 2,5m
l = ld + lg = 6,35 m
v= ld / l = 4,0285/6,2839 =0,64
![]()
= tgα → h1 = 4,05∗ tgα = 1,64m
![]()
= tgα→ h2 =0,74m
Wysokość teoretyczna słupa:
h = h1 + 1,08 = 1,64+1,08 = 2,72m
ZESTAWIENIE OBCIĄŻEŃ
Ciężar pokrycia blacho-dachówką stalową o grubości 0,55mm wg PN-82/B-02001
2.1.1. Wartość charakterystyczna obciążenia gk = 350 N/m2(połaci dachu)
2.1.2. Wartość obliczeniowa gd = gk ∗ γf = 350∗1,2 = 420 N/m2
Obciążenie śniegu wg PN-80/B-02010
Obciążenie charakterystyczne dachu Sk :
Sk = Qk∗C
Qk - obciążenie charakterystyczne śniegiem gruntu (kN/m2)
dla I strefy wg punktu 3 tabl. 1 Qk= 0,7 kN/m2
C - współczynnik kształtu dachu wg Z1-1
C = C2 = 1,2∗(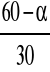
) = 1,2∗(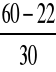
) = 1,52
Sk = 0,7∗1,52= 1,064 kN/m2 = 1064 N/m2 (rzut dachu na powierzchnię poziomą)
Obciążenie obliczeniowe śniegiem
Sd = Sk ∗ γf = 1064∗1,4 = 1489,6 N/m2
S⊥= S ∗ cos2α
S║= S ∗ cosα ∗sin α
Obciążenie wiatrem wg PN-77/B-02011
Obciążenie charakterystyczne
pk = gk ∗ Ce∗ C ∗β
pk - obciążenie charakterystyczne
gk - charakterystyczne ciśnienie prędkości wiatru ( zależne od strefy wiatrowej)
Ce - współczynnik ekspozycji zależny od rodzaju terenu i wielkości budynku
Teren dzielimy na 3 klasy:
Klasa A - teren otwarty z nielicznymi przeszkodami
Klasa B - teren zabudowany przy wysokości istniejących budynków do 10m lub zalesiony
Klasa C - teren zabudowany przy wysokości istniejących budynków powyżej 10m
C - współczynnik aerodynamiczny
C = Cz - Cw
Cz - współczynnik ciśnienia zewnętrznego zależny od ၧ
ၧ = ![]()
% gdy ၧ <35% (dla budowli zamkniętych) Cw = 0
Strona nawietrzna
Cz = 0,015α - 0,2 = 0,015 ∗ 22 - 0,2 =0,13
Cw= 0
C= Cz =0,13
Strona zawietrzna
Cz = -0,13
Cw= 0
C= Cz = -0,13
β - współczynnik działania porywu wiatru zależny od rodzaju budynków
a) - budynki niepodatne na dynamiczne działanie wiatru β = 1,8
b) - budynki podatne na dynamiczne działanie wiatru - β - określamy na podstawie obliczeń teoretycznych.
Qk = 250 Pa - dla I strefy wiatrowej
Ce= 0,8
β = 1,8
Obciążenie charakterystyczne wiatrem od strony nawietrznej
pk1 = 250∗0,8∗0,13∗1,8 = 46,8 Pa
Obciążenie charakterystyczne wiatrem od strony zawietrznej
pk2 = 250∗0,8∗(-0,13)∗1,8 = -46,8 Pa
Obciążenie obliczeniowe
pd = pk ∗ γf
Strona nawietrzna
Pd1 = 46,8 ∗1,3 = 60,84 N/m2
Strona zawietrzna
Pd2 = -46,8 ∗1,3 = -60,84 N/m2
Obciążenie |
Wartości charaktery-styczne N/m2 |
Współ-czynnik obciążenia γf
|
Wartości obliczeniowe N/m2 |
Składowe prostopadłe obciążenia |
Składowe równoległe obciążenia |
||
|
|
|
|
Wartość charakterysty-czna |
Wartość obliczeniowa |
Wartość charakterystyczna |
Wartość obliczeniowa |
Ciężar pokrycia dachówką karpiówką |
qk = 350 |
1,2 |
qd = 420 |
qk⊥ =324,5 |
qd⊥ =389,4 |
qk =131,1 |
qd =157,3 |
Śnieg |
Sk =1064 |
1,4 |
Sd =1489,6 |
Sk⊥ =914,42 |
Sd⊥ =1280,6 |
Sk =369,6 |
Sd =517,4 |
Wiatr -połać nawietrzna -połać zawietrzna |
pk1 =46,8 pk2 = -46,8 |
1,3 1,3
|
pd1 =60,84 pk2 = -60,84
|
pk⊥1 =46,8 pk⊥2 = -46,8
|
pd⊥1 =60,84 pd⊥2 = -60,84
|
- - |
- - |
Suma obciążeń -strona nawietrzna -strona zawietrzna';;;;;;;;'''''''''''''''';;;;;;;;;;;;;;: |
- -
|
- - |
- - |
qk⊥1 =1286 qk⊥2 =1192,4 |
qd⊥1=1730,9 qd⊥2 =1609,2 |
qk1 =500,7 qk2 =500,7 |
qd1 =674,7 qd2 =674,7 |
2.4. Zestawienie obciążeń połaci dachowych
OBLICZENIE KROKWI PODCIĘTEJ NAD PŁATWIĄ POŚREDNIĄ
3.1. Sprawdzenie naprężeń ( pierwszy stan graniczny)
3.1.1. Zestawienie obciążeń.
Obciążenie prostopadłe od połaci dachowej działające:
od strony nawietrznej
q′d⊥1 = qd⊥1· a=1730,9·1,14=1973,2 N/m
od strony zawietrznej
q′d⊥2 = qd⊥2· a = 1609,2·1,14 =1834,5 N/m
Obciążenie równoległe do połaci dachowej
od strony nawietrznej
q′d 1= qd 1·a =769,2 N/m
od strony zawietrznej
q′d 2= q′d 1
Krokiew liczymy jako belkę wolnopodpartą o długości ![]()
. Naprężenia sprawdzamy z uwzględnienie wyboczenia w płaszczyźnie z - x (prostopadłej do powierzchni dachu).
Wyboczenia w płaszczyźnie y - x (równoległej do powierzchni dachu) nie sprawdza się z uwagi na usztywnienie krokwi za pomocą łat.
3.1.2. Maksymalny moment zginający w przęśle
MAD = 0,125· q′d⊥1 · ![]()
=0,125·1973,2 ·4,372 =4710,25 Nm
3.1.3. Siła podłużna (ściskająca)
N = q′d 1·![]()
=769,2 ·![]()
=1680,7 N
3.1.4. Potrzebny wskaźnik wytrzymałości
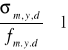
![]()
=![]()
![]()
![]()
![]()
![]()
![]()
=![]()
kmod- częściowy współczynnik modyfikacyjny, uwzględniający wpływ na właściwości wytrzymałościowe czasu trwania obciążenia i zawartości wilgoci w konstrukcji, zależny od klasy użytkowania konstrukcji i od klasy trwania obciążenia.
Kmod=0,9 -przyjęto dla warunków użytkowania=1, klasa trwania obciążenia-krótkotrwale
γm=1,3
![]()
= ![]()
=20,77 Mpa
![]()
=![]()
=![]()
=0,00022678 m3 =226780 mm3
Założono przekrój krokwi 60x200 mm (b x h)
Dla takiego przekroju:
A=12000 mm2
![]()
=![]()
=![]()
=40000000 mm4
![]()
=400000mm3
iy= ![]()
=57,7 mm
3.1.5. Sprawdzenie naprężeń (ściskanie i zginanie z uwzględnieniem wyboczenia)
![]()
+![]()
+![]()
![]()
gdzie:
- ![]()
- naprężenia obliczeniowe od ściskania ![]()
=![]()
-![]()
- obliczeniowa wytrzymałość na ściskanie
-![]()
, ![]()
- naprężenia obliczeniowe od zginania w stosunku do osi głównych pokazanych na rysunku
- ![]()
, ![]()
- odpowiadające tym naprężeniom wytrzymałości obliczeniowe na zginanie
Wartości współczynnika km należy przyjmować następująco
km= 0,7 dla przekrojów prostokątnych
km= 1,0 dla innych przekrojów
![]()
- powierzchnia obliczeniowa przekroju poprzecznego, w mm2
![]()
=![]()
=![]()
=0,14 N/ mm2
![]()
=8,0 Gpa
![]()
= 1,0 - dla prętów na obu końcach opartych przegubowo na podporach nieprzesuwnych
![]()
![]()
=![]()
= 1,0·4,37=4,37 m
![]()
=![]()
=![]()
=75,74
![]()
=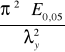
=![]()
=13,76 Mpa
![]()
=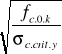
=1,29
![]()
=0,5·![]()
=1,41
![]()
= 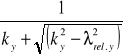
=0,5
![]()
=![]()
Mpa
![]()
=![]()
=![]()
= 11,77 Mpa
![]()
![]()
![]()
= ![]()
=20,77 Mpa
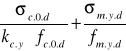
+0 = 0,58< 1
3.2. Sprawdzenie stanu granicznego użytkowalności (ugięć)
Z uwagi na małą wartość naprężeń od siły osiowej, wpływ tej siły na ugięcie krokwi pominięto.
3.2.1. Ugięcie od obciążenia stałego (ciężar własny krokwi i pokrycia)
![]()
= ![]()
·(1+![]()
)
![]()
=0,6
![]()
=21,85 > 20
Dla elementów o stałym przekroju prostokątnym
![]()
![]()
=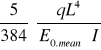
![]()
<20 ![]()
![]()
+![]()
=![]()
·[1+19,2·(![]()
)2]
![]()
=12,0 Gpa
![]()
=40000000 mm4
![]()
=![]()
·a=324,5·1,14=369,93 N/m = 0,3699 N/mm
![]()
=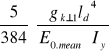
= ![]()
= 3,66 mm
![]()
=0,6
![]()
=![]()
·(1+![]()
) = 5,02·(1+0,6) = 5,85 mm
3.2.2. Ugięcie od obciążenia śniegiem
![]()
=0,25
![]()
= Sk⊥ · a = 914,42 · 1,14 =1042,4 N/m = 1,042 N/mm
![]()
=![]()
·![]()
=10,31
![]()
=![]()
·(1+![]()
)= 20,14·(1+0,25) = 12,88 mm
3.2.3. Ugięcie od obciążenia wiatrem
![]()
= 0
![]()
= ![]()
46,8·1,14 = 53,352 N/m = 0,053352 N/mm
![]()
=![]()
·![]()
= 0,53 mm
![]()
=![]()
= 0,53 mm
3.2.4. Ugięcie całkowite:
ufin = ufin1 + ufin2 + ufin3 = 5,85 + 12,88 + 0,53 = 19,26 mm
3.2.5. Ugięcie dopuszczalne
![]()
![]()
=![]()
=21,85 mm
![]()
OBLICZANIE PŁATWI POŚREDNIEJ
4.1. Sprawdzenie naprężeń.
4.1.1. Zestawienie obciążeń
ciężar własny
![]()
- własność charakterystyczna ciężaru płatwi.
![]()
- wartość obliczeniowa tego obciążenia.
Obciążenie |
Wartość charakterystyczna [N/m2] |
Współczynnik obciążenia γf |
Wartość obliczeniowa [N/m2] |
Obciążenie pionowe Ciężar pokrycia gk Obciążenie śniegiem Sk cosα=1064·0,9272 Obciążenie wiatrem (połać nawietrzna) pk1 cosα=46,8·0,9272 Razem: |
350
986,54
46,2 qk,z = 1382,74 |
1,2
1,4
1,3
|
420
1381,2
60 qd,z = 1861,2 |
Obciążenie poziome Obciążenie wiatrem (połać nawietrzna) pk1sinα = 46,8·0,3746 |
qk.y = 17,53 |
1,3 |
qd,y=22,8 |
Obciążenie pionowe przypadające na 1 mb płatwi
qd,z,1 = qd,p + qd,z(0,5 + Ig) = 7747,77N/m
Obciążenie poziome przypadające na 1 mb płatwi
Qd,y,1 = qd,y(0,5Id + Ig) = 94,92N/m
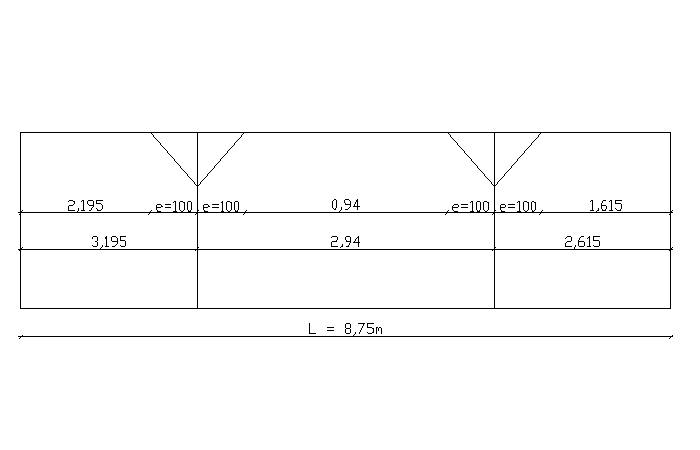
Rozpiętość między murami L = 8,75 m
e = 1,0 m
e < l1/3 = 0,87 m
l1,z = l3,z = l1 - e = 5,28 - 1,0 = 1,615 m l1,y = l3,y = 2,615 m
l2z = l2 - 2e = 5,4 - 2,0 = 1,94 m l2,y = 2,94 m
Obliczanie płatwi jako belki jednoprzęsłowej o skończonej rozpiętości l jest dopuszczalne gdy obciążenie zmienne p nie jest większe niż 10000 N/mb długości belki, a stosunek obciążenia zmiennego do stałego jest mniejszy niż 2 ( p/g <2 ). Gdy w poszczególnych przęsłach występuje obciążenie ruchome lub gdy rozpiętości sąsiednich przęseł różnią się więcej niż 20% należy przeprowadzić dokładne obliczenia.
4.1.2. Momenty zginające:
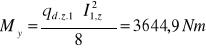
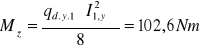
4.1.3. Potrzebny wskaźnik wytrzymałości.
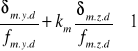
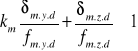
![]()
km = 0,7 - dla przekrojów prostokątnych
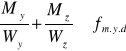
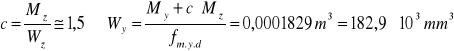
Przyjęto płatew o wymiarach 14x24 cm
A = 336 cm2 = 33600mm2
Iy = 16128 cm4 = 161280000 mm4
Iz = 5488 cm4 = 54880000 mm4
Wy = 1344 cm3 = 1344000 mm3
Wz = 784 cm3 = 784000 mm3
4.1.4 Sprawdzenie naprężeń.
-w płaszczyźnie pionowej.
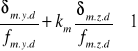
, czyli 0,135<1
![]()
=0,7 - dla przekrojów prostokątnych
-w płaszczyźnie poziomej:
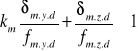
, czyli 0,098<1
4.2 Sprawdzenie stanu granicznego używalności (ugięcia).
4.2.1. Ugięcie w płaszczyźnie pionowej.
4.2.1.1. Ugięcie od obciążenia stałego.
![]()
![]()
g k.z.1 = 1,558 N/mm
u inst,z,1 = 0,15 mm
u fin,z,1= u inst,z,1*(1+k def)=0,24
4.2.1.2. Ugięcie od obciążenia śniegiem
![]()
S k,z=4,11 N/mm
u fin,z,2= u inst,z,2*(1+k def)=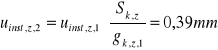
0,49
4.2.1.3 Ugięcie od obciążenia pionowego wiatrem.
![]()
p k,z = 0,18 N/mm
u fin,z,3=0,02 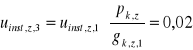
4.2.2. Ugięcie od obciążenia poziomego wiatrem.
Pk,y=73,02M/m=0,073 N/mm
u inst,y=0,11
u fin,y= u inst,y*(1+kdef)=0,11mm
4.2.3. Ugięcie finalne
![]()
= ![]()
0,24+0,49+0,02=0,75 mm
![]()
= 0,11 mm
![]()
![]()
= 0,76 mm
Wartość graficzna ugięcia
![]()
= ![]()
![]()
=9,7 mm ![]()
= 14,7 mm
![]()
= ![]()
17,61 mm
![]()
0,76 mm < ![]()
= 17,61 mm
SPRAWDZENIE WARUNKU STATECZNOŚCI PRZY ZGINANIU
![]()
![]()
- współczynnik stateczności giętej (jego wartość zależy od smukłości sprowadzonej ![]()
)
Dla przekrojów prostokątnych
![]()
= 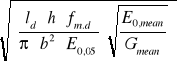
![]()
= 1940 mm ![]()
12,0 Gpa =12000 Mpa
![]()
20,77 ![]()
0,75 Gpa = 750 Mpa
h = 240 mm ![]()
8,0 Gpa = 8000 Mpa
b = 140 mm
![]()
=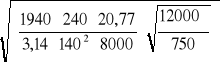
=0,28 < 0,75
![]()
= 1,0 dla ![]()
![]()
= 2,71 Mpa
![]()
1,0·20,77 = 20,77 Mpa
![]()
2,71 Mpa < ![]()
20,77 Mpa
OBLICZENIA SŁUPA
6.1. Siła ściskająca w słupie
Nd = q d.z.1 · ( 0,5l 1.z + e + l 2.z + e ) ![]()
29267N
6.2. Projektowanie słupa
Przyjęto przekrój słupa 14 x 14 cm (140 x 140 mm)
Ad = 19600 mm2
iy = iz = 40,4 mm
6.3. Sprawdzanie naprężeń ściskających
σc.0.d = ![]()
![]()
kc - współczynnik wyboczeniowy
kc.y = ![]()
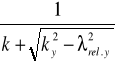
(kc.z = kcy - przekrój kwadratowy)
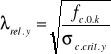
(![]()
rel.z = ![]()
rel.y)
ky=0,5[1+βc(![]()
rel.y - 0,5) + ![]()
] (kz = ky)
βc - współczynnik dotyczący prostoliniowości elementów (dla drewna litego βc = 0,2)
![]()
= π2·E0.05/![]()
(![]()
=![]()
)
![]()
y=![]()
(![]()
z = ![]()
y ![]()
![]()
= ![]()
)
lc.y - wysokość teoretyczna słupa lc.y = h = 266cm = 2,66m
lc.y = ![]()
(lc.z = lc.y ![]()
![]()
)
lc.y = 1,0·2,66 = 2,66m
![]()
y = 65,82
![]()
![]()
= 18,23 Mpa
![]()
rel.y = 1,12
![]()
ky = 1,19
kc.y= 0,63
σc.0.d = 2,38Mpa < f![]()
Mpa
SPRAWDZENIE NAPRĘŻEŃ W PODWALINIE.
Σc.90.d ≤ kc.90·fc.90.d
k c,90 - współczynnik, który uwzględnia możliwość zwiększenia wytrzymałości kiedy długość obciążonego odcinka, wynikająca z rozkładu sił, oznaczona jako l jest mała
f c,90,d - obliczeniowa wytrzymałość na ściskanie prostopadle do włókien
fc.90.d = ![]()
l - długość docisku (l=140 mm)
kc.90 = 1+ (150 - l)/170 = 1,059
Powierzchnia docisku:
Ac.90 = ![]()
![]()
![]()
![]()
(<kc.90 · fc.90.d = 4,18 Mpa)
PROJEKTOWANIE MIECZY.
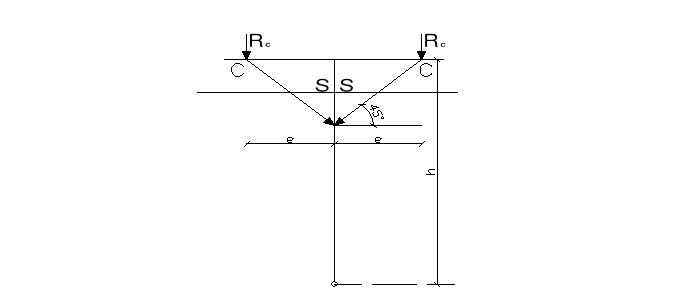
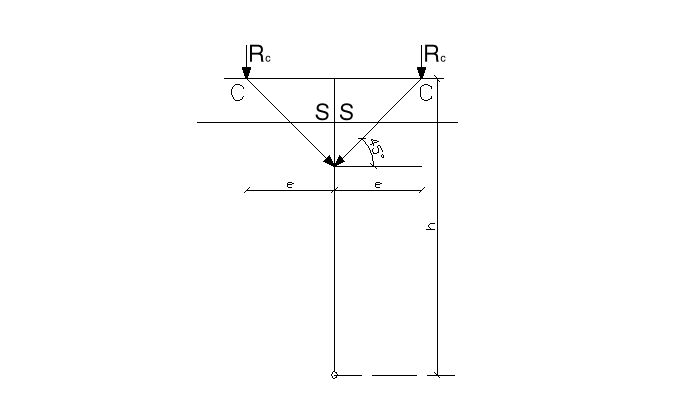
8.1. Siły w mieczach.
SL = RCL /sinα
SP = RCP / sinα
RCL = RL + IMCLI /e
RCP = RP + IMCLI /e
MCL = (-qd.z.1 ·e2 / 4) · [(1 + ![]()
) / (2 + 3 mL)]
mL = ![]()
![]()
MCL= - 1474,93 Nm
MCP= - 2056,177 Nm
![]()
![]()
![]()
(![]()
=45o ![]()
sin![]()
= 0,7071)
![]()
Długość wyboczeniowa mieczy - Im = 1,41m
Założono przekrój mieczy 100mm x 100mm
Ad = 10000mm2
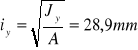
![]()
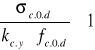
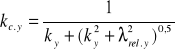
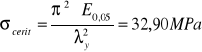
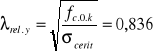
![]()
![]()
![]()
WYMIAROWANIE KLESZCZY
(Pk = 1,0 KN - człowiek z narzędziami)
(Długość kleszczy lk = 367 cm
Siła ściskająca
Nd = qd.y.1 ·l2.y = 279,07 N
Siła skupiona powodująca zginanie
Pd = Pk · γf =1,0 · 1,2 = 1,2 KN = 1200 N
Moment zginający
![]()
OBLICZENIE STROPU:
Strop DZ-3 jednostronnie częściowo zamocowany oparty na ścianach grubości
0,25 m (b1=b2=0,25m).
Rozpiętość modularna stropu LM=6,00m. Na stropie ustawiona jest ścianka działowa z cegły dziurawki grubości 0,12m o wysokości 2,5m (ściana usytuowana prostopadle do rozpiętości stropu obustronnie otynkowana tynkiem cem.-wap. Grubości 0,015m).
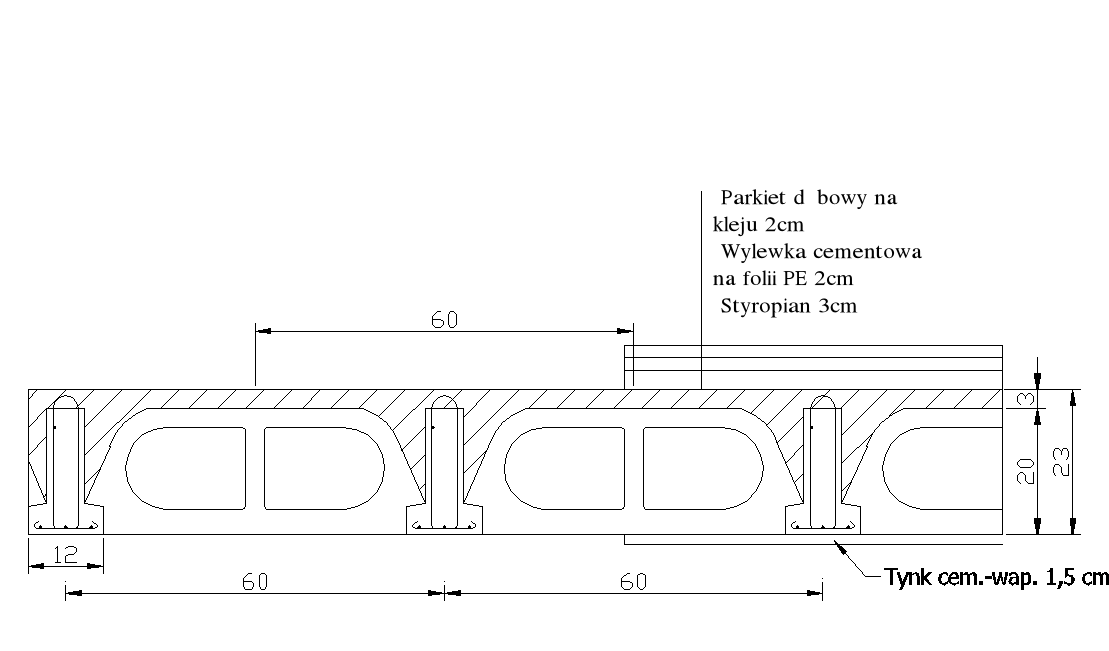
Obciążenia działające na strop.
Obciążenie od warstw wykończeniowych - podłogowych.
-parkiet dębowy na kleju 0,025m (γf=1,2)
γp=7,0 kN/m3 0,025*7,0=0,175kN/m2 0,175kN/m2*1,2=0,21kN/m2
- wylewka cementowa na folii PE 0,02m (γf=1,3)
γc=21,0 kN/m3 0,03*21,0=0,63 kN/m2 0,63kN/m2*1,3=0,819 kN/m2
- styropian 0,03m (γf=1,2)
γs=0,45 kN/m3 0,04*0,45=0,018 kN/m2 0,018 kN/m2*1,2=0,0216 kN/m2
gd,w=1,0506 N/m2
Ciężar własny konstrukcji stropu (pustaki żużlobetonowe).
(γf=1,1) gk,str.=2,650 kN/m2 gd,str.=1,1*2,65=2,915 kN/m2
Tynk cementowo-wapienny grubości 0,015m. (γf=1,3)
γt=19,0 kN/m3 gk,t=0,015*19,0=0,285kN/m2 gd,t=1,3*0,285=0,37kN/m2
Obciążenie użytkowe (zmienne) (γf=1,4) PN-82/B-02003 p.3.2 tabl. 1
pk =1,20 kN/m2 pd =1,4*1,2=1,68 kN/m2
2.Obciążenie ścianką działową otynkowaną.
Od obciążenia ścianką usytuowana prostopadle do układu belek stropowych przyjmuje się obciążenie zastępcze. PN-82/B-02003 p.3.4 tabl. 3
γmuru=14,50 kN/m3
γtynku=19,00 kN/m3
Ciężar 1m2 ściany gś=0,12*14,50+2*0,015*19=2,31 kN/m2
Przyjęto obciążenie zastępcze dla ściany (γf=1,3).
gk,z =1,25 kN/m2
gz=1,25*2,5/2,65*1,3=1,53 kN/m2
3.Zebranie obciążeń na 1mb belki.
6,02+1,53*0,6=6,938
4.Długość obliczeniowa belki.
Ustalenie rozpiętości obliczeniowej
leff = Ls + a
Ls - rozpiętość stropu w świetle ścian
Ls = LM - (b1=b2)/2 =6,00-(0,25+0,25)/2=5,75m.
a - rzeczywista głębokość oparcia stropu
a = (Lrz - Ls)/2
Lrz - rzeczywista długość belki stropowej (4 cm mniejsza niż długość modularna)
Lrz = 5,96m
a = (5,96-5,75)/2=0,105m
leff = 5,75+0,105= 5,855m
Moment przęsłowy
Mprzęsłowy=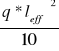
=![]()
=23,78 kNm
Moment podporowy
Mpodporowy=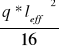
=![]()
=14,87 kNm
Z uwagi na maksymalny moment przęsłowy przyjęto 23,78 nie można z tabel odczytać zbrojenia belki , gdyż największy moment przęsłowy z tabeli równy 23,258kNm< 23,78. W takim przypadku należy zastosować żebro rozdzielcze w stropie.
Zaprojektować żebra jednostronnie częściowo zamocowanego stropu DZ-3 o rozpiętości modularnej LM=6,00m. Rozpiętość stropu w świetle ścian L0 = 5,75m. Strop oparty na ścianach grubości 0,25m. Na żebrze stoi ścianka działowa z cegły dziurawki obustronnie otynkowana ustawiona wzdłuż zebra. Wysokość kondygnacji budynku wynosi 2,5m. Ze względu na ciężar ścianki przewiduje się zastosowanie zebra podwójnego, przyjęto, że żebro to przejmie cały ciężar ścianki.
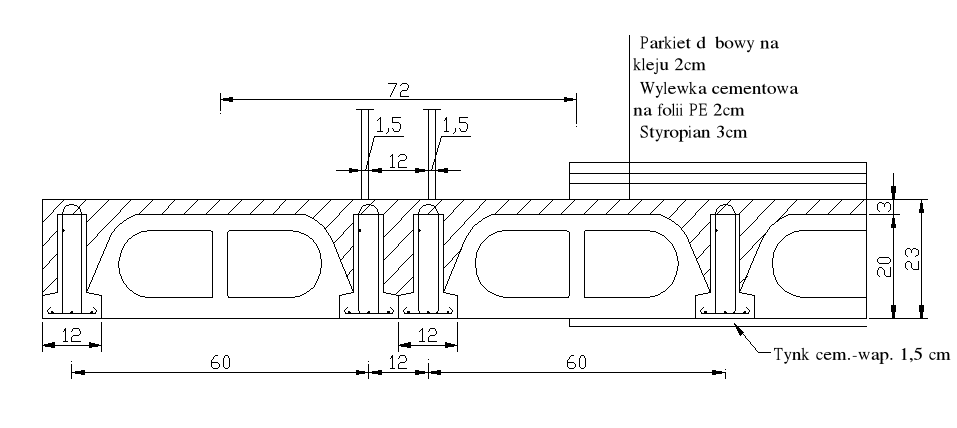
Zestawienie obciążeń dla żebra podwójnego pod ścianką (uwzględniono redukcję obciążenie zmiennego i obciążenia od warstw podłogowych ze względu na usytuowanie ścianki grubości 12 cm).
- parkiet, cement, styropian gd,w=1,0506*(0,72-0,09)=0,662 kN/m
- konstrukcja stropu - żebro podwójne
gd,str.=2,65*0,6*1,1+0,12*0,23*0,24*1,1=2,4776 kN/m
- tynk
gd,t=0,015*19*1,3*0,72=0,267 kN/m
- ciężar ścianki
gd,ś= (0,12*14,5*1,2+2*0,015*19*1,3)*(2,5-0,23)=6,422 kN/m
- obciążenie zmienne stropu
pd=1,2*1,4*(0,72-0,09)=1,06 kN/m
Obciążenie całkowite żebra q1=10,89 kN/m
Ustalenie rozpiętości obliczeniowej
leffI = L0 + a
L0 - rozpiętość stropu w świetle ścian
L0 = LM - (b1=b2)/2 =6,00-(0,25+0,25)/2=5,75m.
a - rzeczywista głębokość oparcia stropu
a = (Lrz - L0)/2
Lrz - rzeczywista długość belki stropowej (4 cm mniejsza niż długość modularna)
Lrz = 5,96m
a = (5,96-5,75)/2=0,105m
leffI = 5,75+0,105= 5,855m
Moment przęsłowy
Mprzęsłowy=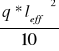
=![]()
=37,33 kNm
Moment podporowy
Mpodporowy=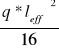
=![]()
=23,33 kNm
Z uwagi na maksymalny moment przęsłowy przyjęto belki nr 11 o dopuszczalnym momencie przęsłowym przenoszonym przez zebro podwójne M = 40,467 kNm > M1= 37,33kNm - zbrojenie główne belki 2Φ12mm + 1Φ10mm.
OBLICZENIA ŚCIANY:
Budynek usytuowany w I strefie obciążenia wiatrem i w I strefie obciążenia śniegiem, zrealizowany w technologii tradycyjnej:
-konstrukcja dachu drewniana z drewna sosnowego klasy C30, dach płatwiowo-kleszczowy, pochylenie połaci α=22°
-pokrycie blachą dachówkową
-stropy żelbetowe gęstożebrowe DZ-3, szerokość wieńców żelbetowych 240mm,wysokość 250mm
-ściany zewnętrzne budynku wykonane z cegły pełnej na zaprawie zwykłej klasy M5 o wytrzymałości na ściskanie fm=5Mpa, izolacja termiczna z wełny mineralnej grubości 120mm, warstwa elewacyjna - cegła pełna120mm, ściana od wewnątrz otynkowana tynkiem cementowo-wapiennym o grubości15mm..
Kategoria produkcji elementów murowych 3.
Kategoria wykonania robót murarskich A.
O nośności ściany decyduje nośność filara międzyokiennego ściany parteru.
1. Dane geometryczne ściany
-szerokość filara b=0,215m
-grubość muru filara t=0,25m
-wysokość ściany w świetle stropów h=2,50m
-szerokość wieńca żelbetowego aw=0,24m
2. Zestawienie obciążeń jednostkowych:
Ciężary objętościowe:
Mur z cegły pałnej γmuru=18kN/m3 γf=1,1
Tynk cementowo-wapienny γtynku=19,00kN/m3 γf=1,3
Żelbet γżelbet=24,0kN/m3 γf=1,1
Wełna mineralna γwełny=1,0 kN/m3 γf=1,2
Drewno γdrew=5,50kN/m3 γf=1,2
A. Dach
Obliczeniowe obciążenia stałe wg PN-82/B-02001
- pokrycie i konstrukcja więźby dachowej (gk=0,35 kN/m2, γf=1,2)
gd=0,42 kN/m2
- ciężar murłaty o przekroju 140x140mm gd,m=0,14*0,14*5,50*1,2=0,129 kN/m
Obliczeniowe obciążenia zmienne
- obciążenie śniegiem wg PN-80/B-02010 dla I strefy obciążenia ( Sk=1,064kN/m2, γf=1,4)
Sd=1,49 kN/m2
- obciążenie wiatrem wg PN-77/B-02011 dla I strefy obciążeń (pk,d=0,047 kN/m2 , γf=1,3)
pd,d=0,06 kN/m2
B.Stropy
Strop poddasza
-konstrukcja stropu gd,str=3,047kN/m2
-warstwy wykończeniowe gd,w=0,624+0,048+0,132+0,296=1,10kN/m2
-obciążenie użytkowe (zmienne) pd,p=2,10kN/m2
Całkowite obciążenie stropów poddasza gd,p=6,25kN/m2
C.Ściana zewnętrzna
- warstwa zewnętrzna (elewacyjna) - mur z cegły pełnej o grubości 0,12m
0,12*18,0*1,1 = 2,376 kN/m2
- izolacja termiczna - wełna mineralna grubości 0,12m
0,12*1,0*1,2=0,144 kN/m2
- warstwa z cegły pełnej grubości 0,25m
0,25*18,0*1,1=4,95 kN/m2
- tynk cem-wap. grubości 0,015m
0,015*19,0*1,3=0,37 kN/m2
Obliczeniowe obciążenie całkowite 7,84 kN/m2
Obciążenie poziome ściany od działania wiatru (ssanie wiatru) wg PN-77/B-0201
γf=1,3
pd,ś=qx*Ce*Cx*βx*γf
I strefa obciążenia wiatrem - wartość charakterystyczna ciśnienia prędkości wiatru
qk=0,25 kPa
Teren typu B zabudowany przy wysokości budynku z<20m Ce=0,8
Współczynnik działania porywu wiatru β=1,8
Współczynnik aerodynamiczny przy, H/L<2
i B/L<1 przy ssaniu wiatru Cx=0,4
pd,ś=0,25*0,8*0,4*1,8*1,3=0,187 kN/m2
Obciążenia pionowe działające na filar (zebrane z pasma obliczeniowego ściany) według zestawienia obciążeń jednostkowych.
Szerokość pasma obliczeniowego ściany, z którego obciążenie będzie się przenosiło na filar
bp=0,5⋅1,6+0,215 + 0,5⋅1,6 = 1,815m
3.1. Obciążenie przekazywane z dachu(ze śniegiem i wiatrem)
(gd+Sd*cosα+pd,d*cosα)*(0,5ld+l1)*bp=(0,42 + 1,49*0,9272+0,06*0,9272)*(0,5*4,37+0,47)*1,815= 8,95 kN
3.2. Obciążenie murłatą gd,m*bp=0,129*1,815=0,234 kN
3.3. Ciężar wieńca żelbetowego 0,24⋅0,25(24,0-18,0)⋅1,815⋅1,1=0,719kN
3.4. Ciężar ściany parteru (1,815*2,5-0,5*1,6*1,50-0,5*1,6*1,5)*7,84 = 16,76 kN
3.5.Obciążenie całkowite ze stropu poddasza 6,25⋅0,5⋅3,06⋅1,815=17,36kN
3.6. Ciężar ściany parteru w połowie wysokości 8,38 kN
Obciążenie poziome od ssania wiatru wd = pd,śbp=0,187*1,815=0,34 kN/m
Sprawdzenie nośności muru.
Przebieg obliczeń przy przyjęciu modelu przegubowego
N1,R,d=Φ1*A*fd>N1,d
Nm,R,d=Φm*A*fd>Nm,d
N2,R,d=Φ2*A*fd>N2,d
A=0,25*0,215=0,05m2
fd - wytrzymałość obliczeniowa muru na ściskanie fd = fk/γm*ηA
fk - wytrzymałość charakterystyczna na ściskanie
-elementy murowe grupy 3,dla fb=10MPa i fm=5,0MPa fk=2,3MPa
γm - współczynnik bezpieczeństwa muru dla I kategorii produkcji elementów murowych i kategorii A wykonania robót γm=1,7
ηA-współczynnik zależny od pola przekroju muru (dla przekrojów <0,3m2 odczytujemy z tabeli)
przy A=0,05m2 mamy ηA=2
fd=2,3/1,7*2=0,68 MPa
Φi - współczynniki redukcyjne nośności
Φi(1,2)-współczynnik redukcyjny zależny od wielkości mimośrodu ei, na którym w rozpatrywanym przekroju działa siła pionowa Ni,d oraz od wielkości mimośrodu niezamierzonego ea
Φm - współczynnik redukcyjny wyrażający wpływ efektów drugiego rzędu na nośność ściany zależy od:
- mimośrodu początkowego (e0=em)
- smukłości ściany (heff/t)
- cech sprężystych muru pod obciążeniem długotrwałym (αc,∞) i czasu działania obciążenia
Wpływ długotrwałego obciążenia na nośność ściany uwzględnia się przyjmując do wyznaczenia wartości współczynnika redukcyjnego nośności Φm - długotrwały moduł sprężystości muru E∞
Cechy sprężyste muru pod obciążeniem długotrwałym określa współczynnik αc,∞
αc,∞= αc/(1+ηE*Φ∞)
ηE<1 - współczynnik uwzględniający:
- zmniejszenie pełzania muru na skutek redystrybucji sił wewnętrznych w konstrukcji
- stosunek obciążenia działającego długotrwale do obciążenia całkowitego elementu konstrukcji murowej
Φ∞ - końcowa wartość współczynnika pełzania
αc - cecha sprężystości muru
Jeżeli nie jest wymagana duża dokładność obliczeń można przyjąć ηE=0,3 Φ∞=1,5
oraz αc,∞=700-dla murów na zaprawie fm≥5MPa z wyjątkiem murów z bloczków z betonu komórkowego
Obciążenia występujące w sprawdzanych przekrojach muru
Siła ściskająca w poziomie stropu nad parterem
N1,d=8,95+0,234+0,719+17,36=27,26kN
Siła ściskająca przekazywana ze stropu nad sprawdzanym odcinkiem ściany
Nsl,d=0kN
Siła ściskająca pod stropem nad parterem
N1,d,ś=N1,d+Nsl,d=27,26kN
Siła ściskająca w przekroju środkowym ściany
Nm,d=N1,d,ś+8,23=27,26+8,38=35,64kN
Siła ściskająca w przekroju nad stropem w dolnej części ściany
N2,d=N1,d,ś+16,76=27,26+16,67=44,02kN
Wartości współczynników redukcyjnych nośności
-w przekroju pod stropem nad parterem
Φ1-1-2e1/t
e1=M1,d/(N1,d+Nsl,d)
M1,d=N1,d⋅ea+Nsl,d(0,33t+ea)
ea-mimośród przypadkowy (niezamierzony)≥10mm
ea=h/300=2500/300=8,33mm<10mm
przyjęto ea=10mm=0,01m
M1,d=27,26⋅0,01=0,2726kNm
e1=0,2726/(27,26)=0,01m
Φ1=1-2⋅0,01/0,24=0,92
-w przekroju nad stropem w dolnej części ściany
Φ2=1-2⋅e2/t
e2=M2,d/N2,d
M2,d=N2,d⋅ea=44,02⋅0,01=0,4402kNm
e2=0,4402/44,02=0,01m
Φ2=1-2⋅0,01/0,24=0,92
-w przekroju środkowym ściany
Φm-odczytujemy z tabeli
1. αc,∞=700
2.Smukłość ściany heff/t
heff-wysokość obliczeniowa ściany heff=ρh⋅ρn⋅h
ρh-współczynnik wyrażający wpływ warunków podparcia ściany w poziomie stropów ,jeżeli konstrukcja usztywniona jest przestrzennie w sposób eliminujący przesów poziomy ρh=1,0
ρn-współczynnik wyrażający wpływ usztywnienia obliczanej ściany wzdłuż krawędzi pionowych-dla ściany podpartej u góry i u dołu dla modelu przegubowego ρn=1,0
heff=1,0⋅1,0⋅2,5=2,5m
heff/t=2,5/0,24=10,42
3.mimośrodu początkowego em (em/t=x em=x⋅t)
em=em,0+em,w
em,0-mimośród początkowy od obciążenia pionowego
em,w-mimośród dodatkowy od obciążenia poziomego
em,0=( 0,6M1,d+0,4M2,d)/Nm,d=(0,6⋅0,2726+0,4⋅0,4402)/35,64=0,009m
em.w=Mw,d/Nm.d
Mw,d=0,125⋅wd⋅h2=0,125⋅0,34⋅2,52=0,27kNm em,w=0,27/35,64=0,0076m
em=0,009+0,0076=0,0166m
em/t=0,0166/0,24=0,07
αc,∞=700
heff/t=10,42 Φm=0,78
em=0,07t
Φ1=0,92 N1,R,d=Φ1⋅A⋅fd=0,92*0,05*680=31,28kN > N1,d,ś=27,26kN
Φm=0,78 Nm,R,d=Φm⋅A⋅fd=0,78*0,05*680=26,52kN < Nm,d=35,64kN
Φ2=0,92 N2,R,d=Φ2⋅A⋅fd=0,92*0,05*680=31,28kN < N2,d=44,02kN
Nośność filara nie jest wystarczająca. W tym celu należy poszerzyć filar.
2
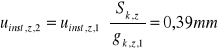
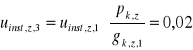
Wyszukiwarka