3. EKSTREMA FUNKCJI WIELU ZMIENNYCH

Definicja 3.21 (ekstrema lokalne funkcji)

Niech
, gdzie
. Funkcja
ma w punkcie
maksimum lokalne, jeżeli

.

Funkcja
ma w punkcie
maksimum lokalne właściwe, jeżeli

.

(
oznacza otoczenie punktu
, zaś
sąsiedztwo punktu
)

Analogicznie określa się minimum lokalne w punkcie
oraz minimum lokalne właściwe.

Twierdzenie 3.22 (Warunek konieczny istnienia ekstremum)

Jeżeli funkcja
, (gdzie
), ma w punkcie
różniczkę
oraz ma ekstremum lokalne w punkcie
, to
.

Uwaga 9. Z warunku istnienia różniczki
wynika, że

dla
.

Twierdzenie 3.23 (I Warunek wystarczający istnienia ekstremum)

Załóżmy, że funkcja
, gdzie
, ma ciągłe pochodne cząstkowe rzędu drugiego w
oraz
. Wówczas jeśli niezdegenerowana forma kwadratowa
jest dodatnio (ujemnie) określona, to funkcja
ma minimum (maksimum) lokalne w
, zaś jeśli
jest nieokreślona, to
nie ma ekstremum lokalnego w
.

Uwaga 10. Przypomnijmy, że

, gdzie

oraz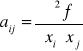
. Forma kwadratowa
jest niezdegenerowana, jeśli

.

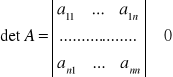
Twierdzenie 3.24 (II Warunek wystarczający istnienia ekstremum)

Załóżmy, że funkcja
, gdzie
, ma ciągłe pochodne cząstkowe rzędu drugiego w
oraz
. Wówczas jeśli

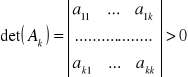
dla
,

gdzie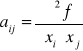
, to funkcja
ma w punkcie
minimum lokalne właściwe, natomiast jeśli
, to
ma w punkcie
maksimum lokalne właściwe.

Definicja 3.25 (Wyznacznik funkcyjny, inaczej jakobian)

Jeśli funkcje
,
mają pochodne cząstkowe w pewnym obszarze
, to wyznacznikiem funkcyjnym lub jakobianem nazywamy

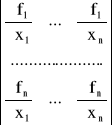
i oznaczamy
.

Twierdzenie 3.26 Niech funkcje
dla
mają ciągłe pochodne cząstkowe w obszarze
oraz funkcje
dla
są określone w obszarze
. Jeśli spełniony jest warunek

gdy
, to
,

wówczas

.

Definicja 3.27 (ekstrema warunkowe funkcji)

Niech
, gdzie
. Mówimy, że funkcja
ma w punkcie
minimum lokalne właściwe przy warunku
, (gdzie
), jeśli
oraz istnieje taka liczba
, że

.

Twierdzenie 3.28 (Warunek konieczny istnienia ekstremum warunkowego)

Jeżeli funkcje
i
mają ciągłe pochodne cząstkowe rzędu pierwszego w obszarze

, to warunkiem koniecznym istnienia ekstremum warunkowego w punkcie
przy warunku
jest aby

w punkcie
.

4. FUNKCJA UWIKŁANA

Definicja 3.29 (Funkcja uwikłana)

Funkcją uwikłaną określoną przez warunek
nazywamy każdą funkcję
spełniającą równość

dla wszystkich
z pewnego przedziału
.

Podobnie określa się funkcję uwikłaną postaci
, gdzie
(
oznacza pewien przedział).

Twierdzenie 3.30 (o istnieniu i różniczkowalności funkcji uwikłanej)

Niech funkcja
ma ciągłe pochodne cząstkowe rzędu pierwszego na otoczeniu
, gdzie
oraz niech spełnia warunki:

(1)
,

(2)
.

Wówczas na pewnym otoczeniu
istnieje jednoznacznie określona funkcja uwikłana
spełniająca warunki:

dla każdego

oraz

i

dla każdego

.

Ponadto, jeśli
ma ciągłe pochodne cząstkowe drugiego rzędu na otoczeniu
, to funkcja uwikłana
jest dwukrotnie różniczkowalna na pewnym otoczeniu punktu
i jej druga pochodna wyraża się wzorem

.

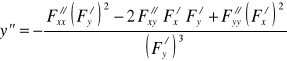
Uwaga 11. Łatwo widać, że jeżeli dla funkcji uwikłanej
określonej równaniem
zachodzi warunek:
, to

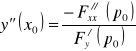
, gdzie
i
.

Twierdzenie 3.31 (o ekstremach lokalnych funkcji uwikłanej)

Niech funkcja
ma ciągłe pochodne cząstkowe rzędu drugiego na otoczeniu

oraz niech spełnia warunki:

(1)
,
,

(2)
,

(3)

,

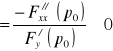
gdzie
. Wtedy funkcja uwikłana
określona przez równanie
ma w punkcie
ekstremum lokalne właściwe i jest to:

minimum, gdy

,

albo maksimum, gdy

.

Uwaga 12.

Równość
jest warunkiem koniecznym, a układ
i
warunkiem wystarczającym istnienia w punkcie
ekstremum funkcji uwikłanej określonej przez równanie
. Prawdziwe jest także analogiczne twierdzenie o ekstremach funkcji uwikłanej postaci
.

IV CAŁKI WIELOKROTNE

1.CAŁKI PODWÓJNE

Definicja 4.1 (Łuk zwykły)

Krzywą
określoną równaniami parametrycznymi

,
dla

nazywamy łukiem zwykłym, jeśli
i
są funkcjami ciągłymi na przedziale
oraz różnym wartościom parametru
odpowiadają różne punkty krzywej
. Jeśli ponadto
, to łuk zwykły
nazywamy zamkniętym.

Uwaga 1. Krzywa
, która jest wykresem funkcji ciągłej
dla
(lub
dla
) jest łukiem zwykłym.

Definicja 4.2 (Obszar regularny)

Ograniczony obszar
nazywamy regularnym, gdy brzeg tego obszaru jest sumą skończonej liczby łuków zwykłych danych równaniami:

dla
lub
dla
,

przy czym łuki te mogą redukować się do punktów.

Definicja 4.3 (Całka podwójna)

Niech
będzie funkcją określoną na domkniętym regularnym obszarze
i niech
oznacza podział obszaru
w dowolny sposób na
domkniętych obszarów częściowych
odpowiednio o polach
,
, w ten sposób, aby:

1. żadne dwa obszary
   ,
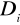
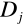
   dla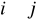
   nie miały wspólnych punktów wewnętrznych,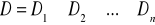

2. 
   .

Liczbę

, gdzie
jest średnicą zbioru
,

nazywamy średnicą podziału
.

W każdym obszarze
wybieramy punkt pośredni
, (
) i tworzymy sumę całkową

.

Jeżeli dla każdego ciągu
podziałów obszaru
na obszary częściowe spełniającego warunek
i dla każdego wyboru punktów pośrednich w obszarach częściowych istnieje ta sama skończona granica ciągu
sum całkowych funkcji
, to granicę tę nazywamy całką podwójną funkcji
na obszarze
i oznaczamy

.

Funkcję
, dla której istnieje całka podwójna na obszarze
nazywamy funkcją całkowalną na obszarze
.

Własności całki podwójnej

Twierdzenie 4.4 (Warunek konieczny całkowalności)

Jeżeli funkcja
jest całkowalna na domkniętym regularnym obszarze
, to jest funkcją ograniczoną na tym obszarze.

Twierdzenie 4.5 (I Warunek wystarczający całkowalności)

Jeżeli funkcja
jest ciągła na domkniętym i regularnym obszarze
, to jest funkcją całkowalną na obszarze
.

Twierdzenie 4.6 (II Warunek wystarczający całkowalności)

Jeżeli funkcja
jest ograniczona na domkniętym i regularnym obszarze
oraz jest ciągła na tym obszarze z wyjątkiem skończonej liczby łuków zwykłych o równaniach
lub
zawartych w obszarze
, to
jest funkcją całkowalną na obszarze
.

Twierdzenie 4.7

Jeżeli funkcja
jest całkowalna na domkniętym i regularnym obszarze
, zaś ograniczona funkcja
pokrywa się z funkcją
poza skończoną liczbą łuków zwykłych o równaniach
lub
zawartych w obszarze
, to funkcja
też jest całkowalna na
oraz

.

Twierdzenie 4.8

Jeżeli funkcje
i
są całkowalne na domkniętym, regularnym obszarze
, to

1. dla dowolnej liczby
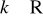
   funkcja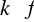
   jest całkowalna na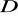
   oraz

;

2. funkcja
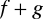
   jest też funkcją całkowalną na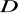
   oraz

.

Twierdzenie 4.9 (addytywność całki względem obszaru całkowania)

Załóżmy, że domknięty regularny obszar
jest sumą domkniętych regularnych obszarów
i
nie mających wspólnych punktów wewnętrznych. Wówczas funkcja
jest całkowalna na obszarze
wtedy i tylko wtedy, gdy jest całkowalna na każdym z obszarów
i
, przy czym

.

Twierdzenie 4.10 (monotoniczność całki podwójnej)

Jeżeli funkcje
i
są całkowalne na domkniętym regularnym obszarze
oraz
dla
, to

.

Twierdzenie 4.11

Jeżeli funkcja
jest funkcją całkowalną na domkniętym i regularnym obszarze
oraz
dla każdego
, to
.

Definicja 4.12 (Wartość średnia funkcji na obszarze)

Wartością średnią funkcji
na obszarze
nazywamy liczbę

.

Twierdzenie 4.13 (o wartości średniej dla całek podwójnych)

Niech funkcja
będzie ciągła na obszarze normalnym
. Wówczas

istnieje punkt
, dla którego zachodzi równość

.

Twierdzenie 4.14 (o zamianie całki podwójnej na iterowaną)

1. Jeżeli funkcja
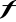
   jest ciągła na obszarze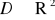
   normalnym względem osi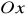
   ,

przy czym

,

to

.

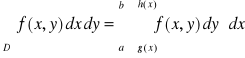
2. Jeżeli funkcja
jest ciągła na obszarze
normalnym względem osi
,

przy czym

,

to

.

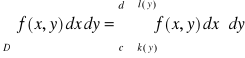
3. W szczególnym przypadku, gdy obszar
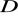
   jest prostokątem o bokach

równoległych do osi
i
, przy czym

oraz
jest ciągła na
, to

=
.

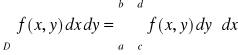
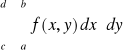
Uwaga 2. Z definicji obszaru normalnego względem osi
(względem osi
) wynika, że jest on obszarem domkniętym i regularnym,

Dowodzi się również, że każdy domknięty regularny obszar
jest sumą skończonej liczby obszarów normalnych względem osi
(osi
) takich, które nie mają wspólnych punktów wewnętrznych.

Zamiana zmiennych w całce podwójnej

Definicja 4.15 (przekształcenie obszarów na płaszczyźnie)

Niech
i
będą obszarami odpowiednio w płaszczyznach
i
. Przekształceniem obszaru
w obszar
nazywamy funkcję
określoną wzorem

, gdzie
.

Obrazem zbioru
przy przekształceniu
jest zbiór

.

Przekształcenie
nazywamy:

1. ciągłym, jeżeli funkcje
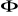
   i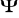
   są ciągłe na obszarze
   ;

2. wzajemnie jednoznacznym, jeśli różnym punktom obszaru
   odpowiadają różne punkty jego obrazu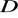
   .

Uwaga 3. Obraz obszaru przy przekształceniu ciągłym i wzajemnie jednoznaczny jest

również obszarem .

Twierdzenie 4.16 (o zamianie zmiennych w całce podwójnej)

Niech

1. odwzorowanie
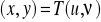
   , gdzie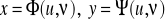
   , przekształca wzajemnie jednoznacznie wnętrze obszaru regularnego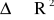
   na wnętrze obszaru regularnego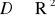
   ,

2. funkcje
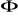
   i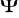
   mają ciągłe pochodne cząstkowe na pewnym zbiorze otwartym zawierającym obszar
   ,

3. funkcja
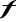
   jest ciągła na obszarze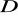
   ,

4. jakobian
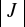
   przekształcenia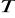
   jest różny od zera wewnątrz obszaru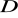
   .

Wówczas

.

Definicja 4.17 (współrzędne biegunowe)

Położenie punktu na płaszczyźnie można opisać parą liczb
, gdzie:

• 
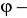
  oznacza miarę kąta między dodatnią częścią osi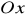
  a promieniem wodzącym punktu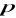
  ,
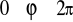
  ( albo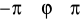
  ) ,

• 
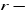
  oznacza odległość punktu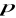
  od początku układu współrzędnych,
  .

Parę liczb
nazywamy współrzędnymi biegunowymi punktu płaszczyzny.

Uwaga 4. Zależność między współrzędnymi biegunowymi i kartezjańskimi określają wzory:

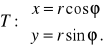
Przekształcenie
, które punktowi
przyporządkowuje punkt
określone powyższymi wzorami nazywamy przekształceniem biegunowym.

Łatwo zauważyć, że jakobian tego przekształcenia

.

Współrzędne biegunowe stosujemy głównie wtedy, gdy obszar całkowania jest ograniczony łukami okręgów o środku w początku układu oraz odcinkami prostych przechodzących przez początek układu.

Zastosowania geometryczne całek podwójnych

Uwaga 5. Zauważmy, że jeśli podzielimy obszar
na
obszarów częściowych
(
) spełniających warunki z definicji całki podwójnej, w każdym obszarze wybierzemy punkt
i rozważymy walce

,
,

to objętość
każdego z walców
jest równa

,
,

(gdzie
oznacza pole obszaru
), a więc sumy całkowe

.

Zatem możemy podać następującą interpretację geometryczną całki podwójnej:

Całka podwójna funkcji
ciągłej i nieujemnej na domkniętym obszarze regularnym
jest objętością obszaru przestrzennego

,

co zapisujemy

.

W szczególności, gdy funkcja
dla
, wtedy obszar przestrzenny
określony powyżej jest walcem o wysokości 1 i podstawie
. Zatem
, a więc

.

Twierdzenie 4.18 (o objętości obszaru przestrzennego)

Jeżeli obszar przestrzenny
określony jest następująco:

oraz funkcje
i
są ciągłe na domkniętym, regularnym obszarze
, to objętość
obszaru
jest równa

.

Definicja 4.19 (Płat powierzchniowy)

Zbiór punktów
, gdzie
jest funkcją ciągłą na domkniętym obszarze
, nazywamy płatem powierzchniowym.

Jeżeli ponadto obszar
jest regularny, zaś funkcja
posiada ciągłe pochodne cząstkowe pierwszego rzędu na
, to płat powierzchniowy
nazywamy regularnym.

Uwaga 6. Płat powierzchniowy regularny ma tę własność, że w każdym punkcie posiada płaszczyznę styczną zmieniającą się w sposób ciągły od punktu do punktu.

Twierdzenie 4.20 (pole płata powierzchniowego)

Jeśli
jest płatem powierzchniowym regularnym określonym za pomocą funkcji
(tzn.
ma ciągłe pochodne cząstkowe pierwszego rzędu na obszarze domkniętym, regularnym
), to pole
płata powierzchniowego
wyraża się wzorem

.

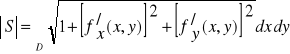
1.CAŁKI POTRÓJNE

Definicja 4.21 (obszar normalny względem płaszczyzn układu współrzędnych)

Obszar domknięty
nazywamy obszarem normalnym względem płaszczyzny
, jeśli można go zapisać w postaci

,

gdzie
jest obszarem regularnym na płaszczyźnie
, funkcje
i
są ciągłe na
, przy czym

dla
.

Można zauważyć, że jeśli
jest obszarem normalnym względem płaszczyzny
, to obszar płaski
jest rzutem obszaru
na tę płaszczyznę.

Analogicznie definiuje się obszary przestrzenne normalne względem płaszczyzny
oraz obszary normalne względem płaszczyzny
.

Definicja 4.22 (obszar regularny w przestrzeni)

Sumę skończonej liczby obszarów normalnych względem płaszczyzn układu współrzędnych o parami rozłącznych wnętrzach nazywamy obszarem regularnym w przestrzeni.

Analogicznie jak całkę podwójną na obszarze płaskim
definiuje się całkę potrójną funkcji trzech zmiennych na obszarze przestrzennym
. Całka potrójna ma również podobne własności jak całka podwójna.

Definicja 4.23 (całka potrójna)

Niech
będzie funkcją określoną na domkniętym, regularnym obszarze
i niech
oznacza podział obszaru
w dowolny sposób na
domkniętych obszarów częściowych
odpowiednio o objętościach
,
, w ten sposób, aby:

1. żadne dwa obszary
   ,
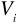
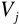
   dla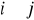
   nie miały wspólnych punktów wewnętrznych,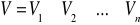

2. 
   .

Liczbę

, gdzie
oznacza średnicę zbioru
,

nazywamy średnicą podziału
.

W każdym obszarze
wybieramy punkt pośredni
, (
), i tworzymy sumę całkową

.

Jeżeli dla każdego ciągu
podziałów obszaru
na obszary częściowe spełniającego warunek
i dla każdego wyboru punktów pośrednich w obszarach częściowych istnieje ta sama skończona granica ciągu
sum całkowych funkcji
, to granicę tę nazywamy całką potrójną funkcji
na obszarze
i oznaczamy

.

Funkcję
, dla której istnieje całka potrójna na obszarze
nazywamy funkcją całkowalną na obszarze
.

Własności całki potrójnej

Twierdzenie 4.24 (Warunek konieczny całkowalności)

Jeżeli funkcja
jest całkowalna na domkniętym, regularnym obszarze
, to jest funkcją ograniczoną na tym obszarze.

Twierdzenie 4.25 (Warunek wystarczający całkowalności)

Jeżeli funkcja
jest ciągła na domkniętym i regularnym obszarze
, to jest funkcją całkowalną na obszarze
.

Uwaga 7. Objętość obszaru domkniętego, regularnego
wyraża się wzorem

Twierdzenie 4.26

Jeżeli funkcje
i
są całkowalne na domkniętym, regularnym obszarze
, to

1. dla dowolnej liczby
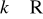
   funkcja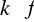
   jest całkowalna na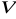
   oraz

;

2. funkcja
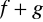
   jest też funkcją całkowalną na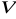
   oraz

.

Twierdzenie 4.27 (addytywność całki względem obszaru całkowania)

Załóżmy, że domknięty, regularny obszar
jest sumą domkniętych regularnych obszarów
i
nie mających wspólnych punktów wewnętrznych. Wówczas funkcja
jest całkowalna na obszarze
wtedy i tylko wtedy, gdy jest całkowalna na każdym z obszarów
i
, przy czym

.

Twierdzenie 4.28 (monotoniczność całki potrójnej)

Jeżeli funkcje
i
są całkowalne na domkniętym regularnym obszarze
oraz
dla
, to

.

Twierdzenie 4.29

Jeżeli funkcja
jest funkcją całkowalną na domkniętym i regularnym obszarze
oraz

dla każdego
,

to

.

Definicja 4.30 (Wartość średnia funkcji na obszarze przestrzennym
)

Wartością średnią funkcji
na domkniętym, regularnym obszarze
nazywamy liczbę

,

gdzie
oznacza objętość obszaru
.

Twierdzenie 4.31 (o wartości średniej dla całek potrójnych)

Jeżeli funkcja
jest ciągła na domkniętym, regularnym obszarze
, to istnieje

taki punkt
, że

.

Twierdzenie 4.32 (o całkach iterowanych)

Jeżeli funkcja
jest ciągła na domkniętym obszarze

,

normalnym względem płaszczyzny
, gdzie funkcje
i
są ciągłe na obszarze regularnym
, to

.

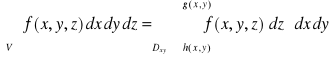
Uwaga 8.

(a) Prawdziwe są także analogiczne wzory z całkami iterowanymi dla funkcji
ciągłej na obszarach normalnych względem pozostałych płaszczyzn układu współrzędnych.

(b) Jeżeli obszar
normalny względem płaszczyzny
można zapisać w postaci

,

to zachodzi równość

.

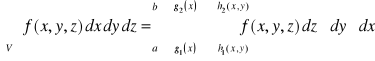
(c) W szczególnym przypadku, gdy funkcja
jest ciągła na domkniętym prostopadłościanie

,

to zachodzi równość

.

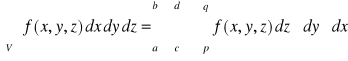
Ponadto ostatnia równość pozostaje prawdziwa, gdy po prawej stronie zmienimy kolejność całkowania (tzn. napiszemy inny rodzaj całki iterowanej).

Zamiana zmiennych w całkach potrójnych

Twierdzenie 4.33 (o zamianie zmiennych w całkach potrójnych)

Niech odwzorowanie
,
, określone następująco:

odwzorowuje wzajemnie jednoznacznie wnętrze obszaru domkniętego, regularnego U na wnętrze obszaru domkniętego, regularnego
, przy czym funkcje
,
,
mają ciągłe pochodne cząstkowe pierwszego rzędu w
. Jeżeli funkcja
jest ciągła w obszarze
oraz jakobian przekształcenia

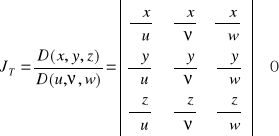
wewnątrz obszaru
,

to

.

Definicja 4.34 (współrzędne walcowe)

Położenie punktu
w przestrzeni
można opisać trójką liczb
, gdzie:

• 
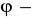
  oznacza miarę kąta między rzutem promienia wodzącego punktu
  na płaszczyznę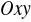
  a dodatnią częścią osi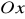
  ,
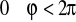
  (albo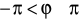
  ),

• 
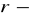
  oznacza odległość rzutu punktu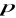
  na płaszczyznę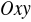
  od początku układu współrzędnych,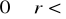
  ,

• 
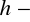
  oznacza odległość punktu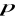
  od płaszczyzny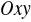
  poprzedzoną znakiem ,,+” dla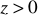
  i poprzedzoną znakiem ,,_” dla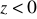
  ,
  .

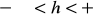
Trójkę liczb
nazywamy współrzędnymi walcowymi punktu przestrzeni
.

Uwaga 9. Zależność między współczynnikami walcowymi i kartezjańskimi podaje przekształcenie
określone wzorami

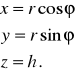
Powyższe przekształcenie
, które punktowi
przyporządkowuje punkt
nazywamy przekształceniem walcowym. Jakobian tego przekształcenia
.

Definicja 4.35 (współrzędne sferyczne)

Położenie punktu
w przestrzeni
można opisać trójką liczb
, gdzie:

• 
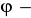
  oznacza miarę kąta między rzutem promienia wodzącego punktu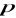
  na płaszczyznę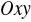
  a dodatnią częścią osi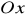
  ,
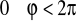
  (albo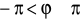
  );

• 
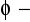
  oznacza miarę kąta między promieniem wodzącym punktu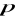
  a płaszczyzną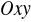
  ,
  ;

• 
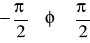
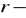
  oznacza odległość punktu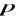
  od początku układu współrzędnych,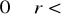
  .

Trójkę liczb
nazywamy współrzędnymi sferycznymi punktu przestrzeni.

Uwaga 10. Zależność między współrzędnymi sferycznymi i kartezjańskimi podaje przekształcenie
przyporządkowujące punktowi
punkt
według wzoru

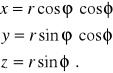
Powyższe przekształcenie
nazywamy przekształceniem sferycznym. Jakobian tego przekształcenia
.

15

---