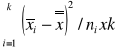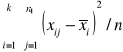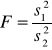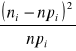1. Przedział ufności dla wskaźnika struktury

Często badanie statystyczne a raczej jej badana cecha ma charakter niemierzalny, jakościowy i wtedy zamiast wartości liczbowej badanej cechy z badania próbnego uzyskujemy jedynie informacje o tym, czy dany element populacji generalnej ma badaną, wyróżnioną cechę jakościową czy też jej nie ma.

Elementy populacji generalnej dzielą się wówczas na dwie klasy:

• elementy wyróżnione,

• elementy niewyróżnione.

Frakcja (wskaźnik struktury populacji) - podstawowy parametr populacji szacowany w przypadku badań statystycznych ze względu na mierzalną cechę elementów wyróżnionych w populacji. Wskaźnik ten jest oznaczany symbolem p.

Przedział ufności dla wskaźnika struktury p , otrzymujemy jak zwykle z odpowiedniego rozkładu estymatora tego parametru. Takim estymatorem jest wskaźnik struktury z próby m/n, gdzie m oznacza liczbę elementów wyróżnionych znalezionych w losowej próbie o liczebności n.

Budowę przedziału ufności dla p w zależności od wielkości próby można oprzeć na dokładnym rozkładzie estymatora m/n lub też na jego rozkładzie granicznym (w przypadku dużej próby).

Najczęściej frakcje p elementów wyróżnionych w populacji szacujemy w oparciu o wyniki dużej próby (n>100). Wówczas można wyznaczyć przybliżony przedział ufności dla parametru p.

Model

Generalna populacja ma rozkład dwupunktowy z parametrem p, tzn. elementy populacji są podzielone na dwie klasy, przy czym frakcja elementów wyróżnionych w populacji wynosi p, które nie jest małym ułamkiem (p>0,05). Z populacji tej wylosowano niezależnie dużą liczbę n elementów do próby (n>100). Wtedy przedział ufności dla wskaźnika struktury p populacji generalnej jest określony przybliżonym wzorem:

(1.0)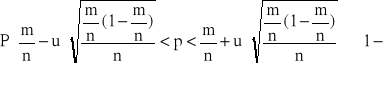

gdzie m jest liczbą elementów wyróżnionych znalezionych w próbie, a u_α jest odczytaną z tablicy rozkładu normalnego N(0,1) wartością zmiennej normalnej standaryzowanej U, w taki sposób, by spełniona była relacja P{- u_α <U< u_α }=1-α dla ustalonego z góry współczynnika ufności 1-α.

Przykład

Chcemy oszacować, jaki procent pracujących mieszkańców Warszawy jada obiady w stołówkach pracowniczych. Pobrano w tym celu n=900 osób wylosowanych niezależnie do próby i znaleziono w tej próbie m=300 osób, które jedzą obiady w stołówkach. Przyjmując współczynnik ufności 1-α=0,95 zbudować przedział ufności dla procentu badanej kategorii pracujących w Warszawie.

Rozwiązanie

Przedział ufności dla szacowanej frakcji p pracowników można wyznaczyć według wzoru (1.0). Dokonujemy niezbędnych obliczeń:

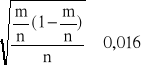
Z tablicy rozkładu normalnego N(0,1) dla 1-α=0,95 tzn. dla α=0,05, znajdujemy wartość u_α. Otrzymujemy przybliżony przedział ufności.

0,333 -1,96x0,016<p<0,333+1,96 x 0,016 tj. 0,302<p<0,364

2. Przedział ufności dla wariancji

Ze względu na cechę mierzalną w badaniach statystycznych do najczęściej szacowanych parametrów populacji obok średniej należy wariancja σ² (lub odchylenie standardowe σ) badanej cechy.

Gdy populacja generalna ma rozkład normalny (lub zbliżony), wtedy można stosować przedział ufności dla wariancji σ² populacji. Budowę przedziału ufności dla wariancji opiera się na rozkładzie statystyki, będącej jej estymatorem.

Najczęściej stosowanymi estymatorami wariancji σ² populacji generalnej są statystyki określone wzorami

(1.1)
oraz

Estymator
jest nieobciążonym estymatorem wariancji σ², podczas gdy s² jest obciążonym estymatorem wariancji σ², ale oba estymatory są równoważne, gdy chodzi o przedział ufności dla wariancji, gdyż

Model I

Populacja generalna ma rozkład normalny N(m,σ) o nieznanych parametrach m i σ. Z populacji tej wylosowano niezależnie do próby n elementów (n<30). Przedział ufności dla wariancji σ² populacji generalnej określony jest wzorem,

(1.2)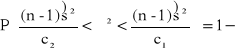

gdzie c₁ i c₂ są wartościami zmiennej χ² wyznaczonymi z tablicy rozkładu χ² dla n-1 stopni swobody oraz współczynnika ufności 1-α w taki sposób, aby spełnione były relacje

,

Model II

Populacja generalna ma rozkład N(m,σ) lub zbliżony do normalnego o nieznanych parametrach m i σ. Z populacji tej wylosowano niezależnie dużą liczbę n elementów. Przybliżony przedział ufności dla odchylenia standardowego σ populacji generalnej jest określony wzorem

(1.3)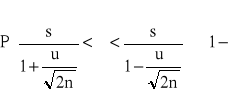

Przykład

Badając wytrzymałość elementu konstrukcyjnego pewnego urządzenia technicznego dokonano n=4 niezależnych pomiarów wytrzymałości i otrzymano następujące wyniki (w kG/cm²); 120, 102, 135, 115.

Należy zbudować przedział ufności dla wariancji σ², wytrzymałości tego elementu, przyjmując współczynnik ufności 1-α=0,96.

Rozwiązanie

Obliczamy z próby wartość ns²,

xi
120 102 135 115	4 256 289 9
472	558

Stąd

Xs = 472:4 = 118 ns²=558.

Z tablicy rozkładu χ² dla n-1=3 stopni swobody odczytujemy dla 1-1/2α=0,98 wartość c₁=0.185 oraz dla 1/2α=0,02 wartość c₂=9.837. Otrzymujemy zatem następujący przedział ufności dla wariancji σ² wytrzymałości:

558: 9,837< σ² <558:0,185, 56,7<σ²<3016

Ze względu na małą liczebność próby otrzymany przedział ufności jest dość szeroki. Chcąc otrzymać przedział ufności dla odchylenia standardowego σ, pierwiastkujemy końce powyższego przedziału i otrzymujemy (z ufnością 0.96) przedział ufności dla σ (w kG/cm²):

7,5<σ<54,9

3. Test dla wartości średniej populacji

Weryfikacja (testowanie) hipotez statystycznych jest drugim obok estymacji rodzajem wnioskowania statystycznego.

Weryfikacja hipotezy statystycznej odbywa się przez zastosowanie specjalnego narzędzia, zwanego testem statystycznym. Jest to reguła postępowania, która każdej możliwej próbie losowej przyporządkowuje decyzję przyjęcia lub odrzucenia sprawdzanej hipotezy. W zależności od postaci podstawionej hipotezy zerowej H₀ (tzn. bezpośrednio sprawdzanej) oraz postaci hipotezy alternatywnej H₁ (tzn. konkurencyjnej w stosunku do hipotezy zerowej), sposób budowy testu jest różny.

W ogólnej teorii weryfikacji hipotez statystycznych decydujące znaczenie ma jeden typ testów, zwanych testami istotności, w których na podstawie wyników próby losowej podejmuje się jedynie decyzję odrzucenia hipotezy sprawdzanej lub stwierdza się, że brak jest podstaw do jej odrzucenia.

Model I

Populacja generalna ma rozkład normalny N(m,σ). Należy na podstawie wyników próby losowej n-elementowej sprawdzić hipotezę H₀: m=m₀ wobec hipotezy alternatywnej H₁ : m≠m₀.

Test istotności dla hipotezy H₀ jest następujący. Na podstawie wyników próby oblicza się wartość średniej z próby, a następnie wartość zmiennej normalnej standaryzowanej U według wzoru

(1.4)

Z tablicy wartości N(0,1) wyznacza się następnie taką wartość krytyczną u_α, by dla założonego z góry małego prawdopodobieństwa α zachodziła równość P{|U|≥u_α}=α.

Model II

Populacja generalna ma rozkład normalny N(m,σ), przy czym odchylenie standardowe σ populacji jest nieznane. W oparciu o wyniki małej, n-elementowej próby losowej należy zweryfikować hipotezę H₀: m=m₀, wobec hipotezy alternatywnej H₁: m≠m₀.

Obliczamy wartość statystyki t według wzoru,

(1.5)

Model III

Populacja generalna ma rozkład N(m,σ) lub dowolny inny rozkład o średniej wartości m i o skończonej, ale nieznanej wartości wariancji σ². Na podstawie wyników dużej próby losowej (n co najmniej rzędu kilku dziesiątków) z tej populacji należy zweryfikować hipotezę H₀: m=m₀, wobec hipotezy alternatywnej H₁: m≠m₀.

Test istotności tej hipotezy jest analogiczny jak w modelu I.

Przykład 1

Pewien automat w fabryce czekolady wytwarza tabliczki czekolady o nominalnej wadze 250 g. Wiadomo, że rozkład wagi produkowanych tabliczek jest normalny N(m,5). Kontrola techniczna pobrała w pewnym dniu próbę losową 16 tabliczek czekolady i otrzymała ich średnią wagę 244 g. Czy można stwierdzić, że automat rozregulował się i produkuje tabliczki czekolady o mniejszej niż przewiduje norma wadze? Na poziomie istotności α=0.05 zweryfikować odpowiednią hipotezę statystyczną.

Rozwiązanie

Z treści zadania wynika, że należy zweryfikować hipotezę o wartości średniej m. wagi tabliczek czekolady. Stawiamy hipotezę H₀: m=250 g , wobec H₁: m<250 g.

Wobec podejrzenia o zaniżenie wagi tabliczek czekolady, stosujemy odpowiedni dla modelu I test istotności dla średniej, z lewostronnym obszarem krytycznym. Z tablicy rozkładu normalnego N(0,1) odczytujemy taką wartość u_α, że P{U≤u_α}=0,05.= 1.64

(1.4)
= (244-250)/5 x sqrt16 = 24/5 = 4,8

Z próby wyznaczamy wartość u=-4,8

Ponieważ wartość krytyczna u_α,=1.64<4,8 to odrzucamy hipotezę zerową. Oznacza to, że badana partia jednostkowego ciężaru tabliczki czekolady jest zaniżona, a automat dozujący wymaga natychmiastowej regulacji.

Przykład 2

W szpitalu wylosowano niezależnie spośród pacjentów leczonych na pewną chorobę próbę 26 chorych i otrzymano dla nich średnią ciśnienia tętniczego krwi
oraz odchylenie standardowe s=45. Należy na poziomie istotności α=0,05 zweryfikować hipotezę, że pacjenci ci pochodzą z populacji o średnim ciśnieniu tętniczym 120.

Rozwiązanie

Z treści zadania wynika, że odchylenie standardowe populacji nie jest znane, a próby nie można uznać za dużą. Ponadto można przyjąć założenie, że ciśnienie krwi u ludzi ma rozkład normalny.

Mamy zatem do czynienia z modelem II, przy czym odpowiedni test istotności dla tego modelu zastosujemy z dwustronnym obszarem krytycznym. Z tablicy rozkładu t Studenta należy odczytać taką wartość t_α, że dla α=0,05 i dla n-1=25 stopni swobody P{|t_α|≥t}=0,05; wartością tą jest t=2.06. Należy teraz obliczyć z próby wartość statystyki

(1.5)
=(135-120)/45 x 5 =1.67

t=1,67

Porównując wartość t z wartością t_α widzimy, że |t|=1,67<2,06=t_α. Oznacza to, że nie znaleźliśmy się w obszarze krytycznym, zatem nie ma podstaw do odrzucenia hipotezy H₀. Różnica uzyskana z próby nie jest w stosunku do hipotetycznej wartości statystycznie istotna, tzn. da się usprawiedliwić przypadkiem.

4. Test dla dwóch średnich

W praktyce i zastosowaniach statystyki bardzo często zachodzi potrzeba sprawdzenia hipotez dotyczących równości wartości średnich w dwóch populacjach normalnych. Populacje te mogą być tworzone w wyniku oddziaływania na część osobników czynnikiem badawczym, lub układem klasyfikacyjnym lub mogły być tworzone oddzielnie, ale ich przestrzeń zmienności jest tożsama. W praktyce badawczej interesują nas rezultaty w ramach, których czynnik badawczy spowodował wystąpienie tak dużych zmian w populacji, że możemy mówić o wystąpieniu nowej jakości

W zależności od ilości posiadanych o porównywalnych populacjach informacji wyróżnimy trzy modele. W każdym z nich weryfikować można hipotezę H₀: m₁=m₂, czyli m₁-m₂=0, gdzie m₁ i m₂ oznaczają wartości średnie odpowiednio pierwszej i drugiej populacji generalnej. Postać hipotezy alternatywnej H₁ decyduje o rodzaju wybieranego w stosowanym dla hipotezy H₀ teście istotności, jednostronnego lub dwustronnego obszaru krytycznego.

Model I

Badamy dwie populacje generalne mające rozkłady normalne N. W oparciu o wyniki dwu niezależnych prób, odpowiednio o liczebnościach n₁ i n₂, wylosowanych z tych populacji należy sprawdzić hipotezę H₀: m₁=m₂, wobec hipotezy alternatywnej H₁: m₁≠m₂.

Z wyników prób wylosowanych z tych populacji obliczamy wartości średnich
i
, a następnie wartość statystyki U wg wzoru,

(1.6)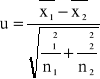

Model II

Badamy dwie populacje generalne mające rozkłady normalne, przy czym odchylenia standardowe tych populacji są nieznane ale jednakowe. Na podstawie wyników dwu małych prób odpowiednio o liczebnościach n₁ i n₂, wylosowanych niezależnie z tych populacji, należy zweryfikować hipotezę H₀: m₁=m₂ wobec hipotezy alternatywnej H₁: m₁≠m₂.

Obliczmy wartość statystyki t według wzoru

(1.7)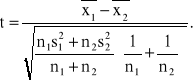

Statystyka ta ma przy założeniu prawdziwości hipotezy H₀ rozkład t Studenta o n₁+n₂-2 stopniach swobody. Z tablicy rozkładu t Studenta należy odczytać wartość dla n₁+n₂-2 stopni swobody oraz dla założonego z góry poziomu istotności α taka wartość krytyczną t_α, by spełniona była równość.

Model III

Badamy dwie populacje generalne mające rozkłady normalne lub inne, byle o skończonych wariancjach
i
, które są nieznane. Na podstawie wyników dwu dużych prób wylosowanych z obu populacji należy sprawdzić hipotezę H₀: m₁=m₂ wobec hipotezy alternatywnej H₁: m₁≠m₂.

Test istotności dla sprawdzanej hipotezy H₀ budujemy analogicznie jak w modelu I, tj. w oparciu o rozkład normalny N(0,1), z tą jedynie różnicą, że przy obliczaniu wartości u zamiast nieznanych wariancji
i
przyjmujemy wartości
i
uzyskane z dużych prób.

Przykład 1

Chcemy stwierdzić, czy słuszne jest mniemanie, że zatrudnione na tych samych stanowiskach w pewnym przemyśle kobiety otrzymują przeciętnie niższą płacę niż mężczyźni. Z populacji kobiet zatrudnionych na określonych stanowiskach wylosowano w tym celu niezależnie próbę n₁=100 kobiet i otrzymano z niej średnią płacę
oraz wariancję
. Z populacji mężczyzn zatrudnionych w tym przemyśle na tych samych stanowiskach wylosowano niezależnie n₂=80 mężczyzn i otrzymano dla nich średnią płacę
oraz wariancję
. Na poziomie istotności α=0,01 należy sprawdzić hipotezę, że średnie płace kobiet są niższe.

Rozwiązanie

Hipotezę badawczą o niższych przeciętnie zarobkach kobiet, zamieniamy na hipotezę statystyczną, że średnie zarobki kobiet m₁ oraz mężczyzn m₂ nie różnią się istotnie i zależy nam oczywiście na odrzuceniu tej ostatniej hipotezy statystycznej. Stawiamy hipotezę H₀: m₁=m₂, wobec hipotezy alternatywnej H₁: m₁<m₂.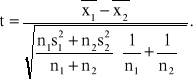
(2180 - 2280)/sqrt(6400/100)+(10000/80) = 100/SQRT 189 = 7.27

Obliczamy teraz wartość u z wyników obu prób losowych u=-7,27.

Z tablicy rozkłady N(0,1) należy odczytać, ze względu na lewostronny obszar krytyczny, w taki sposób krytyczną wartość u_α by P{U≤u_α}=0,01 = 2.33. Znaleźliśmy się w obszarze krytycznym, zatem hipotezę H₀ o równości średnich odrzucamy na korzyść alternatywy H₁.

Zauważmy przy tym, że nawet dla bardzo małego poziomu istotności α, też należałoby ją zadecydowanie odrzucić. Często mówi się wtedy, że otrzymana różnica średnich (100zł) jest statystycznie bardzo istotna.

Otrzymany wynik oznacza, że rzeczywiście w tym przemyśle kobiety zarabiają przeciętnie mniej niż mężczyźni zatrudnieni na tych samych stanowiskach.

Przykład 2

Wysunięto hipotezę, że czas potrzebny na obróbkę pewnego metalowego detalu można zmniejszyć przez zastosowanie innego niż dotychczas typu obrabiarki. Przy niezmienionych innych warunkach, zmierzono dla losowo wybranych sztuk czasy wykonywania tego detalu na dwóch typach obrabiarek i otrzymano dla obrabiarki II (nowej) następujące wyniki (w minutach): 15, 12, 10, 18, 14, 15, 13, a dla obrabiarki I (starej): 17, 11, 22, 18, 19, 13, 14, 16. Zweryfikować wysuniętą hipotezę na poziomie istotności α=0,05.

Rozwiązanie

Mamy do czynienia z modelem II. Stawiamy hipotezę H₀: m₁=m₂, wobec hipotezy alternatywnej H₁: m₁>m₂, gdzie m₁ oznacza średni czas toczenia przy użyciu obrabiarki starej, a m₂ oznacza średni czas toczenia przy użyciu nowo proponowanej obrabiarki.

Z tablicy rozkładu t Studenta należy więc dla α=0,05 oraz dla n₁+n₂-2=13 stopni swobody odczytać taką wartość krytyczną t_α =2.160, by spełniona była nierówność P{t≥t_α}=0,05. Następnie należy wg wzoru (1.7) obliczyć wartość statystyki t. Zauważmy jednak, że

,

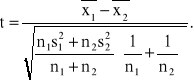
(16 - 14)/sqrt(88-39)/(8+7-2)x(1/8+1/7)

= 2/sqrt2.62 = 1.23

wystarczy zatem obliczyć średnie
i
oraz sumy kwadratów odchyleń od nich.

Otrzymujemy więc wartość statystyki

Ponieważ t_α = 2.160> t =1,23 to nie ma podstaw do odrzucenia hipotezy zerowej. Oznacza to że zakup nowej obrabiarki w celu zwiększenia wydajności pracy jest nieuzasadniony

Zadanie domowe

Niżej zestawiono wyniki dwutygodniowej sprzedaży produktów nabiałowych spółdzielni mleczarskiej „Przyszłość” przed i po zastosowaniu kampanii marketingowej.

Dzień sprzed. Wart sprz. Przed prom Wart. Sprzed po prom

Pon 456 zł 532 zł

Wtor 351 375

Środa 421 495

Czwartek 495 510

Piątek 311 379

Sobota 650 765

Niedziela 234 432

Pon. 486 619

Wtorek 376 438

Środa 478 456

Czwartek 512 543

Piątek 338 456

Sobota 578 650

Niedz 387 398

434,7 503,43

5. Test dla dwóch wskaźników struktury (procentów)

Badając dwie populacje generalne ze względu na cechę niemierzalną musimy często sprawdzać hipotezę, że frakcje elementów wyróżnionych (wskaźniki struktury lub procenty) są w obu populacjach takie same.

Test podany poniżej pozwala na zweryfikowanie tej hipotezy w oparciu o wyniki dwu dużych prób i korzysta się przy tym z asymptotycznego rozkładu normalnego odpowiedniej statystyki. Jak zawsze, w zależności od postaci hipotezy alternatywnej, obszar krytyczny w tym teście buduje się albo dwustronnie, albo też jednostronnie.

Model

Dane są dwie populacje generalne o rozkładach dwupunktowych z parametrami odpowiednio p₁, p₂ (oznaczającymi frakcje elementów wyróżnionych w tych populacjach). Na podstawie dwu dużych prób o liczebnościach odpowiednio n₁ i n₂ (n₁ i n₂ >100) należy sprawdzić hipotezę, że parametry p₁ i p₂ są jednakowe, tzn. H₀: p₁=p₂, wobec hipotezy alternatywnej H₁: p₁
p₂.

Test istotności dla tej hipotezy jest następujący. Z obu prób o liczebnościach n₁ i n₂ wyznaczamy odpowiednie liczby m₁ i m₂ elementów wyróżnionych w tych próbach. Następnie wg wzoru

obliczamy wartość średniego wskaźnika struktury z obu prób
oraz wg wzoru

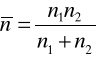
wartość pseudoliczebności próby n. Z kolei obliczamy wartość statystyki

(1.8)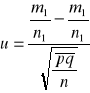
, gdzie

m₁/n₁ i m₂/n₂ są wskaźnikami struktury uzyskanymi z obu prób.

Przykład

W celu sprawdzenia, czy zachorowalność na pylicę jest w pewnym województwie taka sama w mieście jak i na wsi, pobrano z ludności wiejskiej i miejskiej dwie próby, mianowicie z ludności miejskiej wylosowano n₁=1200 osób i otrzymano m₁=40 chorych na pylicę, a z ludności wiejskiej wylosowano n₂=1500 osób i otrzymano m₂=100 osób chorych. Przyjmując poziom istotności α=0,05 należy zweryfikować hipotezę o jednakowym procencie chorych na pylicę w mieście i na wsi w tym województwie.

Rozwiązanie

Zastosujmy powyższy model. Ponieważ nie ma sugestii co to tego, który procent zachorowań na wsi czy w mieście ma być większy, dlatego budujemy dwustronny obszar krytyczny. Formalnie pisząc, stawiamy hipotezę H₀: p₁=p₂, wobec hipotezy alternatywnej H₁: p₁
p₂, gdzie p₁ i p₂ oznaczają nieznane wskaźniki struktury chorych na pylicę odpowiednio w populacji ludności miejskiej i wiejskiej.

Z prób obliczamy

oraz

,

u
-3.9

Z tablicy rozkładu normalnego N(0,1) dla dwustronnego obszaru krytycznego i przy przyjętym poziomie istotności α, odczytujemy krytyczną wartość u_α=1,96. Z porównania wynika, że
, a więc znaleźliśmy się w obszarze krytycznym, zatem hipotezę H₀ odrzucamy. Nie można więc twierdzić, że w tym województwie jednakowa jest zachorowalność na pylicę na wsi i mieście.

6. Test dla dwóch wariancji

W przypadku gdy badanie statystyczne ze względu na pewną cechę mierzalną prowadzimy w dwóch populacjach, może zajść potrzeba sprawdzenia hipotezy o jednakowym stopniu rozproszenia wartości badanej cechy w obu populacjach. Oznacza to sprawdzanie jednorodności dwu wariancji ważne przy stosowaniu testów parametrycznych.

Rozkładem, którym będziemy posługiwać się w omawianym teście, jest rozkład F Snedecora.

Model

Dane są dwie populacje generalne mające odpowiednio rozkłady normalne
i
gdzie parametry tych rozkładów są nieznane. Z populacji tych wylosowano niezależnie dwie próby o liczebności odpowiednio n_l i n₂ elementów. Na podstawie wyników tych prób należy sprawdzić hipotezę Ho:
, wobec hipotezy alternatywnej H₁ :

Przykład

Przed zastosowaniem testu t Studenta dla hipotezy, że średnie zarobki pracowników zatrudnionych na tych samych stanowiskach roboczych w dwu różnych fabrykach są jednakowe, należy sprawdzić założenie tego testu, że wariancje zarobków w obu fabrykach są identyczne. Z jednej fabryki wylosowano w tym celu niezależnie 16 pracowników i otrzymano z tej próby wariancję
=22500 (zł)². Natomiast z drugiej fabryki wylosowano 21 pracowników do próby i otrzymano z niej
=40000 (zł)². Można przyjąć, że rozkłady zarobków w obu fabrykach są normalne. Na poziomie istotności α=0,05 należy sprawdzić hipotezę, że wariancje zarobków badanych pracowników są takie same w obu fabry­kach.

Rozwiązanie

Z danych liczbowych zadania wynika, że aby otrzymać w liczniku statystyki F obliczanej w tym teście większą wartość, należy oznaczyć n₁=21,
=40000 oraz n₂=16,
=22500. Stawiamy hipotezę H₀ :
, wobec hipotezy alternatywnej H_l :

Stosując omówiony powyżej test istotności dla tej hipotezy, obliczamy ze wzoru (2.10) wartość , statystyki F; mamy

F=40000/22500=1,78

Natomiast dla przyjętego poziomu istotności α=0,05 z tablicy rozkładu F Snedecora dla n_l -1=20 oraz n₂-1=15 stopni swobody odczytujemy wartość krytyczną F_α=2,33. Ponieważ nie otrzymaliśmy wartości F z obszaru krytycznego, bo F=1,78<2,33=F_α, zatem nie ma podstaw do odrzucenia hipotezy Ho, że wariancje zarobków w obu populacjach pracowników nie różnią się istotnie.

W następstwie otrzymanego wyniku możliwe jest zastosowanie testu t Studenta dla porównania średnich zarobków w obu fabrykach.

7. Test analizy wariancji (klasyfikacja pojedyncza) dla wielu średnich

Omówione testy t-Studenta oraz testy analizy wariancji, należą do grupy tzw. Testów parametrycznych. Oznacza to, że warunkiem stosowania tych testów jest zgodność rozkładu cech z rozkładem normalnym i jednorodność wariancji(wariancje porównywanych szeregów statystycznych nie różnią się istotnie)

Testy analizy wariancji są podstawowym narzędziem statystyki ekspe­rymentalnej w naukach medycznych, rolniczych i technicznych. Testy te pozwalają na sprawdzenie, czy pewne czynniki, które, można dowolnie regulować w toku eksperymentu, wywie­rają wpływ, a jeśli tak, to jak wielki, na kształtowanie się średnich wartości badanych cech mierzalnych. Istotą analizy wariancji jest rozbicie na audytywne składniki (których liczba wynika z potrzeb eksperymentu) sumy kwadratów wariancji całego zbioru wyników. Porównanie poszczególnej wariancji wynikającej z działania danego czynnika oraz tzw. wariancji resztowej, czyli wariancji mierzącej losowy błąd (które to porównanie odbywa się przez zastosowanie testu F Snedecora) daje odpowiedź, czy dany czynnik odgrywa istotną rolę w kształtowaniu się wyników ekspery­mentu.

Testy analizy wariancji mają bardzo liczne zasto­sowania między innymi w analizie regresji.

Model analizy wariancji dla klasyfikacji pojedynczej

Danych jest k populacji o rozkładzie normalnym
(i =1, 2, ... , k) lub o rozkładzie zbliżonym do normalnego. Zakłada się przy tym, że wariancje wszystkich k populacji są równe, tzn.
(lecz nie muszą być znane). Z każdej z tych populacji wylosowano niezależnie próby o liczebności n_i elementów. Wyniki prób oznaczone są przez x_ij (i=1, 2, ..., k, j=1, 2, ..., n_i) przy czym x_ij=m_i+
, gdzie
jest wartością zmiennej losowej nazywanej składnikiem losowym, mają­cej rozkład
. Na podstawie wyników x_ij należy zweryfikować hipotezę H0 : m₁ = m₂ = ... = m_k wobec hipotezy alternatywnej H_l : nie wszystkie średnie badanych populacji są równe.

Test istotności (analizy wariancji) dla tej hipotezy jest następujący. Obliczamy z wyników poszczególnych prób średnie grupowe
i średnią ogólną
.

(1.9)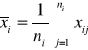
dla i=1,2,...,k

(2.0)
gdzie

Z kolei obliczamy odpowiednie sumy kwadratów i wypełniamy wartościami liczbowymi następującą tablicę analizy wariancji; występująca w niej statystyka F ma przy założeniu prawdziwości hipotezy Ho rozkład F Snedecora o k-1 i n-k stopniach swobody:

Źródło zmienności	Suma kwadratów	Stopnie swobody	Wariancja	Test F
Ogólnej		nxk-1
Między populacjami (grupami)		k-1
Wewnątrz grup (składnik losowy)	Zmienność ogólna - zmienność międzygrupowa	kxn-k

=(
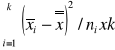
)/ nxk-1
= (
-
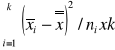
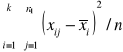
)/ kxn-k

Obliczoną w tablicy analizy wariancji wartość F porównujemy w końcu z wartością krytyczną F_α odczytaną z tablicy rozkładu F Snedecora dla ustalonego z góry poziomu istotności α i dla odpowiedniej liczby k-1 oraz kxn-k stopni swobody. Spełniona ma być przy tym równość P {F
F_α}=α. Jeżeli w wyniku porównania otrzymamy nierówność F
F_α , to hipo­tezę Ho o równości średnich w badanych populacjach należy odrzucić: Natomiast gdy F<F_α , to nie ma podstaw do odrzucenia hipotezy H₀.

Gdy F< 1, to bez porównywania z F_α nie ma podstaw do odrzucenia hipotezy H₀. Odrzucenie hipotezy H₀ oznacza udowodnienie istotnego wpływu podziału na te populacje. W przeciwnym przypadku, wszystkie grupy (populacje) można uznać za równoważne z punktu widzenia otrzymywanych wartości badanej cechy.

Przykład

Koszty materiałowe pewnego wyrobu, który można produkować trzema różnymi metodami, mają rozkład normalny o jednakowej wariancji dla każdej z tych metod. Wylosowane sztuki tego wyrobu dały następujące koszty materiałowe dla poszczególnych metod produkcji (w zł):

Metoda
A	B	C
25 15 20 30 10 - -	40 20 25 50 10 35 -	5 15 20 20 40 10 30

Na poziomie istotności α=0,05 należy zweryfikować hipotezę, że średnie koszty materiałowe są jednakowe dla wszystkich trzech metod produkcji tego wyrobu.

Rozwiązanie

Formalnie biorąc stawiamy hipotezę H₀ : m₁=m₂=m₃, ,gdzie m₁,m₂,m₃ oznaczają średnie koszty materiałowe odpowiednie dla każdej z metod produkcji. Hipotezę tę można zweryfikować za pomocą testu analizy wariancji dla przypadku pojedynczej klasyfikacji. W celu wypełnienia danymi liczbowymi odpowiedniej dla tego testu tablicy analizy wariancji, przeprowadzamy niezbędne obliczenia średnich i sum kwadratów. Z obliczeń tych otrzymujemy

n=n₁+n₂+n₃=18

,
,
,

,
,

,

,
,

Otrzymujemy zatem następującą tablicę analizy wariancji:

Źródło zmienności	Suma kwadratów	Stopnie swobody	Wariancja	Test F
między grupami (metodami)	400,0	2	200,0	F=1,39
Wewnątrz grup (resztkowa)	2150	15	143,3

Z tablicy rozkładu F Snedecora dla przyjętego poziomu istotności α=0,05 i dla liczby stopni swobody 2 i 15 odczytujemy krytyczną wartość F_α=3,68. Ponieważ nie otrzymaliśmy wartości F z obszaru krytycznego, bo F=1,39 < <3;68=F_α, więc nie ma podstaw do odrzucenia sprawdzanej hipotezy Ho o równości średnich kosztów materiałowych przy produkcji tego wyrobu trzema różnymi metodami. Oznacza to, że nie udowodniliśmy, że metody te dają różne średnie koszty materiałowe tego wyrobu. Powodem tego rezultatu jest wysoka wariancja kosztów zużycia materiałów wynikająca przede wszystkim ze zmienności tych kosztów w drugiej technologii.

Przykład marketingowy

Przeprowadzono analizę porównawczą metod promocji

Wartość sprzedaży w tys. zł na dzień dla grupy produktów mleczarskich
	metody promocji
	I	II	III
poniedziałek	3,54	4,43	4,98
wtorek	2,89	3,54	3,55
środa	3,23	3,78	4,5
czwartek	2,75	3,22	4,89
piątek	4,32	4,18	4,67
sobota	4,53	5,03	5,23
niedziela	3,35	4,12	4,65
poniedziałek	3,12	3,98	4,53
wtorek	2,53	3,45	3,87
środa	3,36	3,17	3,67
czwartek	2,65	2,98	3,41
piątek	3,86	3,78	4,08
sobota	4,12	4,57	4,5
niedziela	3,07	4,21	3,99
Suma	47,32	54,44	60,52	Razem
Średnia	3,3800	3,8886	4,3229	162,28
Kwadraty sum	2239,1824	2963,7136	3662,6704	8865,5664
poniedziałek	12,5316	19,6249	24,8004
wtorek	8,3521	12,5316	12,6025
środa	10,4329	14,2884	20,25
czwartek	7,5625	10,3684	23,9121
piątek	18,6624	17,4724	21,8089
sobota	20,5209	25,3009	27,3529
niedziela	11,2225	16,9744	21,6225
poniedziałek	9,7344	15,8404	20,5209
wtorek	6,4009	11,9025	14,9769
środa	11,2896	10,0489	13,4689
czwartek	7,0225	8,8804	11,6281
piątek	14,8996	14,2884	16,6464
sobota	16,9744	20,8849	20,25
niedziela	9,4249	17,7241	15,9201	Razem
Suma	165,0312	216,1306	265,7606	646,9224

Obliczamy sumę kwadratów odchyleń zmienności ogólnej

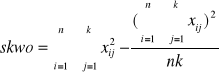
Suma kwadratów odchyleń dla zmienności międzygrupowej

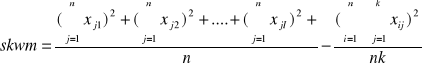
skwm= 633,2547 - 627,019

skwm=6,2357

Suma kwadratów odchyleń zmienności błędu

skwbł=skwo-skwm

skwbł= 19,85-6,2357= 13,61

Źródło zmienności	Suma kwadratów	Stopnie swobody	Wariancja	Test F
Ogólnej	19,85	42-1=41	-
Między populacjami (grupami)	6,2357	3-1=2	6,2357/2=3,1178	8,936**
Wewnątrz grup (składnik losowy)	13,61	3*14-3=39	13,61/39=0,3489

W celu porównania istotności różnic między metodami promocji stosujemy nowy wielokrotny test rozstępu.

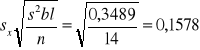
sqrt0,02492

Z tablic wartości krytycznych nowego wielokrotnego testu rozstępu odczytujemy wartości krytyczne dla rozstępu 2 i 3 oraz liczby stopni swobody dla błędu równej 39 wykonujemy następujące obliczenia:

Wyznaczamy przedział ufności

Rozstęp P_0,05 P_0,01 (2) 2,88x0,158 =0,455 3,88x0,158 =0,613

(3) 3,04x0,158 =0,480 4,06x0,158 =0,6415

Rozstęp (2) (3)

Metoda promocji x_śr

III Metoda 4,32

II Metoda 3,89 0,43

I Metoda 3,38 0,51* 0,94**

Analiza istotności różnic pomiędzy średnimi sprzedaży wyrobów uzyskanej po zastosowaniu I, II, i III metody promocji pozwala stwierdzić, że celowe jest zastosowanie III ewentualnie drugiej metody promocji przy rezygnacji ze stosowania metody I.

Schemat dwuczynnikowej analizy wariancji

poniedziałek	3,54	4,43	4,98
Wtorek	2,89	3,54	3,55
Środa	3,23	3,78	4,5
czwartek	2,75	3,22	4,89
Piątek	4,32	4,18	4,67
Sobota	4,53	5,03	5,23
Niedziela	3,35	4,12	4,65
	24,61	28,30	32,47	85,38	4,06

poniedziałek	3,12	3,98	4,53
Wtorek	2,53	3,45	3,87
Środa	3,36	3,17	3,67
czwartek	2,65	2,98	3,41
Piątek	3,86	3,78	4,08
Sobota	4,12	4,57	4,5
Niedziela	3,07	4,21	3,99
	22,71	26,14	28,05	76,9	3,66

Wartości średnie sprzedaży w I tygodniu badań xs-1 = 4.06 a w II tygodniu sprzedaży xs2 = 3,66

skwm= 635,2413 - 627,019

skwm=8,2223

obliczamy sumę kwadratów odchyleń dla okresów tygodni

skwIcz =

obliczamy sumę kwadratów odchyleń dla drugiego czynnika -metody promocji

skwIIcz =

skwIIcz =633,2547 - 627,019

skwIIcz=6,2351

Źródło zmienności	Suma kwadratów	Stopnie swobody	Wariancja	Test F
Ogólnej	19,85	42-1=41	-
Między populacjami (grupami)	8,2223	6-1=5
Zmienność I cz- okresów	1,712	2-1=1	1,712	1,712:0,2836=6.0366*
Zmienność II cz- promocji	6,2351	3-1=2	3,1178	`10,9936**
Zmienność interakcji	0,2752	(2-1)x(3-1)=2	0,1376	0,4852
Wewnątrz grup	11,6277	3*14=42	11,6277:41= 0,2836

Zawarta w tabeli II cz. Analizy wariancji zmienność interakcji obliczana jest następująco:

Skwint = skwm - skwIcz - skw II cz

Skwi = 8,2223 - 1,712-6,2351 = 0,2752

Prezentowane w tabeli wyniki dwuczynnikowej analizy wariancji pozwalają stwierdzić że wyodrębnione czynniki w postaci zmienności sprzedaży w okresach tygodniowych są istotnie zróżnicowane na poziomie istotności α=0,05

Podobnie jak w obliczeniach jednoczynnikowej analizy wariancji otrzymaliśmy istotny wpływ metod promocji na poziomie istotności α=0,01

8. NIEPARAMETRYCZNE TESTY ISTOTNOŚCI

8. Test zgodności
   

Nieparametryczne testy istotności, w których weryfikowana hipoteza dotycząca rozkładu badanej cechy w populacji generalnej nie precyzuje wartości parametrów tego rozkładu, można ogólnie podzielić na dwie grupy. Pierwsza grupa to tzw. testy zgodności, a druga, bardzo liczna, to testy dla hipotezy, że dwie próby pochodzą z jednej populacji (czyli że dwie populacje mają ten sam rozkład.) Jednym z najstarszych testów statystycznych jest test zgodności
. Nazwa jego pochodzi stąd, że statystyka, jakiej używa się przy weryfikacji hipotezy o zgodności próby wyników z rozkładem populacji, ma rozkład asymptotyczny
.

Test zgodności
pozwala na sprawdzenie hipotezy, że populacja ma określony typ rozkładu (tj. określoną postać funkcyjną dystrybuanty). W teście zgodności
próba musi być duża.

Model

Populacja generalna ma dowolny rozkład o dystrybuancie na­leżącej do pewnego zbioru
rozkładów o określonym typie postaci funk­cyjnej dystrybuanty. Z populacji tej wylosowano niezależnie dużą próbę (n co najmniej kilkadziesiąt), której wyniki podzielono na r rozłącznych klas o liczebnościach n_i w każdej klasie, przy czym
. Otrzymano w ten sposób tzw. rozklad empiryczny. Na podstawie wyników tej próby należy sprawdzić hipotezę Ha, że populacja generalna ma rozkład typu
, tzn. Ho : F(x)
S2, gdzie F(x) jest dystrybuantą rozkładu populacji.

Test istotności, zwany testem zgodności, dla tej hipotezy jest następu­jący. Z hipotetycznego rozkładu typu
obliczamy dla każdej z r klas wartości badanej cechy X prawdopodobieństwa p_i, że zmienna losowa X o rozkładzie
przyjmie wartości należące do klasy o numerze i (i=1, 2, ..., r). Z kolei mnożąc p_i przez liczebność całej próby n otrzymuje się liczebności teoretyczne np_i , które powinny były wystąpić w klasie i, gdyby populacja miała rozkład typu
, tzn. gdyby hipoteza Ho była prawdziwa. Ze wszystkich liczebności empirycznych n_i oraz hipotetycznych np_i wyznacza się następnie wartość statystyki

(2.1)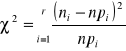

która przy założeniu prawdziwości hipotezy Ho ma rozkład asymptotyczny
o r-1 stopniach swobody lub o r-k-1 stopniach swobody, gdy z próby szacowano k parametrów rozkładu
metodą największej wiarygodności.

Przykład 1

Losowa próba n=200 niezależnych obserwacji miesięcznych wydatków na żywność rodzin 3-osobowych dała następujący rozkład tych wydatków (w tys. zł):

Wydatki	Liczba rodzin
1,0-1,4 1,4-1,8 1,8-2,2 2,2-2,6 2,6-3,0	15 45 70 50 20

Należy na poziomie istotności α=0,05 zweryfikować hipotezę, że rozkład wydatków na żywność jest normalny.

Rozwiązanie

Z treści zadania wynika, że nie są sprecyzowane parametry rozkładu hipotetycznego, stawiamy zatem hipotezę Ho : F(x)
, gdzie
jest klasą wszystkich dystrybuant normalnych. Hipotezę tę weryfikujemy za pomocą testu
. Dwa parametry rozkładu, średnią m i odchylenie standardowe
, szacujemy z próby za pomocą estymatorów uzyskanych metodą największej wiarygodności i uzyskujemy wartości
=2,0 tys. zł oraz s=0,43 tys. zł. Dalsze obliczenia w teście
wygodnie jest przeprowa­dzić tabelarycznie, przy czym niech u_i oznacza standaryzowaną (tj. u_i= =(xi-
)/s) wartość prawego końca przedziału klasowego, a F(u_i) wartość dystrybuanty rozkładu N(0, 1) w punkcie u_i. Mamy

xi	ni	ui	F(ui)	pi	npi	(F-f) x(F-f)
1,4 1,8 2,2 2,6 3,0	15 45 70 50 20	-1,39 -0,46 +0,46 1,39 -	0,082 0,323 0,667 0,918 -	0,082 0,241 0,354 0,241 0,082	16,4 48,2 70,8 48,2 16,4	1,96 10,24 0,64 3,24 12,96	0,12 0,21 0,01 0,07 0,79
	200			1,000	200,0		1,20

Zwróćmy przy tym uwagę, że prawdopodobieństwo dla ostatniego prze­działu wyznaczamy jako 1- F(1,39). Otrzymaliśmy więc wartość statystyki
=1,20: Odpowiednia liczba stopni swobody wynosi 5-2-1=2. Z tablicy rozkładu
dla 2 stopni swobody i dla przyjętego poziomu istotności α=0,05 odczytujemy wartość krytyczną
=5,991.

Ponieważ

nie ma podstaw do odrzucenia hipotezy H₀, że rozkład miesięcznych wydatków na żywność w populacji rodzin 3-osobowych jest normalny.

Przykład 2

Zbadano 300 losowo wybranych 5-sekundowych odcin­ków czasowych pracy pewnej centrali telefonicznej i otrzymano następujący empiryczny rozkład liczby zgłoszeń:

Liczba zgłoszeń	Liczba odcinków
0 1 2 3 4 5	50 100 80 40 20 10

Na poziomie istotności α=0,05 należy zweryfikować hipotezę, że rozkład liczby zgłoszeń w tej centrali jest rozkładem Poissona.

Rozwiązanie

Z treści zadania wynika, że nie jest sprecyzowany parametr
rozkładu Poissona, stawiamy więc hipotezę H₀ : F(x)
,gdzie F(x) jest dystrybuantą rozkładu liczby zgłoszeń, a
klasą wszystkich rozkładów Poissona. Parametr
szacujemy z próby za pomocą jego estymatora uzyskanego metodą największej wiarygodności, którym jest średnia z próby
. Otrzymujemy
=1,7. Przyjmując za
tę wartość, z tablicy rozkładu Poissona odczytujemy prawdopodobieństwa p_i dla każdej kolejnej liczby zgłoszeń i przeprowadzamy tabelarycznie dalsze obliczenia w celu uzyskania wartości statystyki
.

Mamy

xi	ni	pi	npi
0 1 2 3 4 5	50 100 80 40 20 10	0,183 0,311 0,264 0,150 0,064 0,028	54,9 93,3 79,2 45,0 19,2 8,4	24,01 44,89 0,64 25,00 0,64 2,56	0,44 0,48 0,01 0,55 0,03 0,30
	300	1,000	300,0		1,81

Z obliczeń otrzymaliśmy wartość statystyki
=1,81, a dla przyjętego poziomu istotności α=0,05 i dla 6-1-1 =4 stopni swobody odczytana z tablicy rozkładu
krytyczna wartość wynosi
=9,488. Ponieważ
=1,81 < 9,488 =
, więc nie ma podstaw do odrzucenia hipotezy, że rozkład liczby zgłoszeń w tej centrali telefonicznej jest rozkładem Poissona.

9. Test niezależności
   

Często stosowany w praktyce test niezależności
jest testem istotności pozwalającym na sprawdzenie, czy dwie badane cechy (niekoniecznie mierzalne) są niezależne. Test ten oparty jest na tej samej statystyce co test zgodności
, z tym że hipotetycznymi prawdopodobieństwami są oszacowane z próby prawdopodobieństwa otrzymania równocześnie określonej wartości (czy kategorii jakościowej) cechy X oraz Y, przy założeniu niezależności tych cech. Sporządza się zatem odpowiednią tablicę kombinowaną dla dwu cech, zwaną tablicy niezależności, która po wypełnieniu daje macierz liczebności empirycznych. Nakłada się na nią macierz liczebności teoretycznych, obliczonych przy założeniu niezależności cech znajdujących się w główce i w boczku. Porównanie elementów obu macierzy, czego dokonuje się przez zastosowanie statystyki
, daje odpowiedź, czy można odrzucić hipotezę o niezależności cech na skutek wystąpienia zbyt dużych różnic liczebności empirycznych i teoretycznych.

Model

Z populacji tej wylosowano niezależnie dużą próbę o liczebności n elementów. Wyniki próby klasyfikujemy w kombinowaną tablicę niezależności o r wierszach i s kolumnach. Poniższe wzory reprezentują liczebności brzegowe. Zachodzą zatem równości

(2.2)

(2.3)

Z elementów macierzy liczebności empirycznych [n_ij] oraz elementów macierzy liczebności teoretycznych [np_ij] konstruujemy statystykę

(2.4)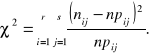

Statystyka ta ma przy założeniu prawdziwości hipotezy H₀ o niezależności cech, asymptotyczny rozkład
z (r-1)(s-1) stopniami swobody.

Przykład

W celu stwierdzenia, czy podanie chorym na pewną chorobę nowego leku przynosi poprawę w ich stanie zdrowia, wylosowano dwie grupy pacjentów w jednakowym stopniu chorych na tę chorobę i jednej grupie o liczebności 120 podawano nowy lek, a druga grupa o liczebności 80 pacjentów otrzymała tradycyjne leki. Po pewnym czasie stwierdzono zestawione w tablicy liczebności chorych w poszczególnych kategoriach stanu zdrowia. Na poziomie istotności a=0,001 zweryfikować hipotezę, że nowy lek istotnie poprawia stan zdrowia pacjentów.

Leczeni	Stan zdrowia po leczeniu
		Bez poprawy	Wyraźna poprawa	Całkowite wyzdrowienie
badanym lekiem	20 39	40 36	60 45
tradycyjnie	45 26	20 24	15 30

65 60 75 200

Występujące w badaniach wyniki reprezentujące badania empiryczne pozwalają wyznaczyć na podstawie proporcji wartości liczebności teoretycznych, które powinniśmy otrzymać gdy badany czynnik nie wpływałby na wyniki leczenia.

X:65 =120:200 X:65=80:200 X:75=120:200

X11 = 65x120/200 = 39 X21 = 65x80/200=26 X13 75x120:200=45

Pozostałe wartości teoretyczne możemy obliczyć z różnic bądź proporcji

Jeżeli częstotliwość empiryczną oznaczymy przez f, a teoretyczną obliczoną z proporcji - przez F, to wartość chi kwadrat obliczamy wg następującego wzoru:

χ2 = (F11-f11)x(F11-f11 )/F11 + +(F23 -f23 )x(F23 -f23 )/F23

χ2o= (39-20)x19/39 + (26-45)x(-19) + (36-40)x(-4) + (24-20)x4 +

+(45-60)x(-15) + (30-15)x15 = 9,2 +13,88 + 0,44 + 0,66 + 5 + 7,5=

= 36,66.

Ponieważ liczba stopni swobody n' = (2-1)x(3-1) = 2 to χ2 0,001=13,815.

Przy χ2o = 36,66 to na poziomie istotności α0,001 odrzucamy hipotezę zerową, co oznacza, że zastosowanie nowego leku decyduje o wynikach leczenia.Rozwiązanie

W inny sposób możemy wykonać obliczenia następująco:

Obliczenia w tekście
niezależności rozpoczynamy od obliczeń liczebności brzegowych n_i. i n._j oraz oszacowania prawdopodobieństw brzegowych p_i. i p._j. Przyjmując następnie założenie o niezależności cech obliczamy prawdopodobieństwa teoretyczne p_ij= p_i.p._j. Wyniki obliczeń prawdopodobieństw p_ij zamieszczone są w prawym górnym rogu każdej kratki. Mnożąc te prawdopodobieństwa przez n=200 otrzymujemy dla każdej kratki liczebności teoretyczne np_ij, które umieszczono w dolnym lewym rogu. Zauważyć przy tym trzeba, że ze względu na konieczność bilansowania się elementów w wierszach i kolumnach obliczenia przeprowadzamy tylko dla tylu kratek, ile wynosi liczba stopni swobody, tzn. (r-1)(s-1)=(2-1)(3-1)=2, a pozostałe elementy zarówno macierzy [p_ij] jak i [np_ij] wyznaczamy z wartości brzegowych.

Leczeni	Stan zdrowia po leczeniu
		Bez poprawy			Wyraźna poprawa			Całkowite wyzdrowienie			ni.	pi.
	Badanym lekiem			0,195			0,180			0,225	120	0,60
		20			40			60
		-39			36			45
	Tradycyjnie			0,130			0,120			0,150			80	0,40
		45			20			15
		26			24			30
n.j	65			60			75			200
p.j	0,325			0,300			0,375				1,00

PRZYKŁAD MARKETINGOWY- 1

W dużej sieci handlowej wprowadzano do sprzedaży trzy nowe asortymenty produktów spożywczych, stosując trzy różne metody promocji stosowane równolegle w trzech podobnych obiektach handlowych. Z systemu informacji handlowej hipermarketu uzyskiwano dane o liczbie klientów kupujących poszczególne asortymenty wyrobów oraz odpowiadające im wartości sprzedaży.

Należy zweryfikować hipotezę zerową o braku zależności pomiędzy stosowanymi metodami promocji a liczbą klientów dokonujących zakupy wprowadzanych do sprzedaży nowych wyrobów.

W poniższej tabeli zamieszczono wyniki dotyczące liczby osób kupujących poszczególne produkty w tyś osób na tydzień

Asort/ met. pro	Metoda1	Metoda2	Metoda3
Produkt 1	3,5	6,7	7,8 18
Produkt 2	11,4	8,9	12,5 32,8
Produkt 3	5,8	5,0	8,9 19,7

Σ 20,7 20,6 29,2 70,5

F11 =5,3 F12 = 5,26 F13 = 7,46 F21 = 9,63 F22 =9,58 F23 = 13,6

F31 = 5,78 F32 = 5,76 F33 =8,16

X = 0,61 +0,39+0,02+0,33+0,05+0,09+0,00+0,1+0,07=1,66

Przykład Marketingowy 2

W ramach trzech kanałów dystrybucji dokonywano działań reklamowo promocyjnych o podobnym poziomie nakładów i dokonywano oceny przyrostu wartości sprzedaży w kolejnych czterech tygodniach. Badanie miało na celu zidentyfikowanie kanału dystrybucji o najwyższym poziomie efektywności reagowania na zastosowane metody reklamy, które kontynuowałoby w przyszłości w tym sektorze.

Wyniki przyrostu sprzedaży w poszczególnych kanałach dystrybucji zestawiono w poniższej tabeli.

Zestawienie przyrostu sprzedaży w kanałach dystrybucji w tyś zł

Tydz sp\ kanały dyst	I kan dyst	II kan. dyst	III kan. dyst	Σ
I tydz	3,2 2,7	3,4 3,6	4,5 4,9	11,1
II tydz	4,4 3,7	4,5 4,8	6,1 6,5	15,0
III tydz	3,7 4,2	5,9 5,5	7,5 7,5	17,1
IV tydz	4,3 5,0	6,6 6.6	9,7 9,0	20,6
Σ	15,6	20,4	27,8	63,8

X = 0,09+0,00+0,3+0,13+0,02+0,03+006+ 0,03+0,00+0,1+0,00+0,05= 0,55

---