RACHUNEK RÓŻNICZKOWY
Niech ![]()
będzie funkcją rzeczywistą zmiennej rzeczywistej
Definicja ilorazu różnicowego
Niech ![]()
oraz ![]()
. Ilorazem różnicowym funkcji ![]()
pomiędzy punktami ![]()
i ![]()
nazywamy liczbę ![]()
.
Załóżmy, że ![]()
wraz z pewnym otoczeniem (otoczeniem lewostronnym, otoczeniem prawostronnym).
Definicja pochodnej .
Pochodną (pochodną lewostronną, prawostronną) funkcji ![]()
w punkcie ![]()
nazywamy granicę ![]()
(![]()
, ![]()
) o ile ona istnieje. Oznaczamy ją wtedy jako ![]()
(![]()
,![]()
).
Definicja różniczkowalności funkcji.
Mówimy, że funkcja ![]()
jest różniczkowalna (różniczkowalna lewostronnie, prawostronnie) w punkcie ![]()
jeśli ma w tym punkcie skończoną pochodną (pochodną lewostronną, prawostronną).
Mówimy, że funkcja ![]()
jest różniczkowalna w przedziale otwartym, jeśli jest różniczkowalna w każdym punkcie tego przedziału.
Mówimy, że funkcja ![]()
jest różniczkowalna w przedziale domkniętym, jeśli jest różniczkowalna w każdym punkcie wewnętrznym tego przedziału, oraz prawostronnie różniczkowalna w lewym krańcu i lewostronnie różniczkowalna w prawym krańcu.
Definicja kąta nachylenia.
Niech ![]()
będzie dowolną prostą na płaszczyźnie![]()
w której![]()
oznacza oś odciętych. Jeśli ![]()
, to przyjmujemy, że kątem nachylenia prostej ![]()
jest zero. Jeśli ![]()
to przyjmujemy, że kątem nachylenia prostej ![]()
jest kąt, którego jednym z ramion jest ![]()
, a drugim odcinek ![]()
przebiegający w górnej półpłaszczyźnie.
Interpretacja geometryczna ilorazu różnicowego i pochodnej.
Prostą przechodzącą przez punkty, ![]()
,![]()
nazywać będziemy sieczną. Zauważmy, że iloraz różnicowy funkcji ![]()
pomiędzy punktami ![]()
i ![]()
jest tangensem kąta nachylenia siecznej. Przy ustalonym ![]()
i ![]()
zmierzającym do ![]()
zauważamy, że sieczne wyznaczone przez te punkty przyjmują w granicy o ile ona istnieje położenie prostej, którą nazwiemy styczną do wykresu funkcji w punkcie![]()
. Pozwala to na spostrzeżenie, że pochodna funkcji jest tangensem kąta nachylenia stycznej do wykresu funkcji w punkcie ![]()
.
Wniosek.
Równanie stycznej do wykresu funkcji w punkcie ![]()
ma postać ![]()
.
Definicja.
Normalną do wykresu funkcji f w punkcie ![]()
nazywamy prostą prostopadłą do stycznej w tym punkcie i przechodzącą przez ten punkt.
Definicja.
Niech funkcje f i g przecinające się w punkcie o odciętej będą różniczkowalne w ![]()
. Kątem przecięcia wykresów funkcji f i g nazywamy nie większy od prostego kąt ![]()
, pomiędzy stycznymi do wykresów tych funkcji w punkcie ich przecięcia.
Wniosek. 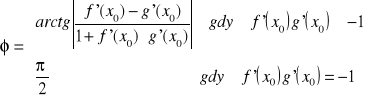
.
Twierdzenie.
Jeżeli funkcja f jest różniczkowalna w pewnym punkcie, to jest w tym punkcie ciągła.
Uwaga. Twierdzenie odwrotne jest fałszywe. (przykład [Author ID0: at Tue Aug 14 13:07:00 2001
][Author ID0: at Tue Aug 14 13:07:00 2001
]![]()
[Author ID0: at Tue Aug 14 13:07:00 2001
])
Twierdzenie.
Jeżeli f i g są różniczkowalne w punkcie ![]()
oraz ![]()
, to funkcje
[Author ID0: at Tue Aug 14 13:07:00 2001
][Author ID0: at Tue Aug 14 13:07:00 2001
]![]()
[Author ID0: at Tue Aug 14 13:07:00 2001
]są różniczkowalne w tym punkcie, oraz prawdziwe są wzory:
[Author ID0: at Tue Aug 14 13:10:00 2001
][Author ID0: at Tue Aug 14 13:10:00 2001
]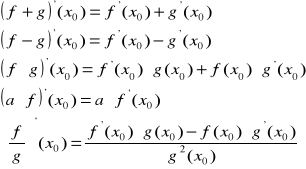
[Author ID0: at Tue Aug 14 13:10:00 2001
]
Ostatni wzór jest prawdziwy przy dodatkowym założeniu, że ![]()
.
Uwaga. Twierdzenie powyższe jest prawdziwe również dla pochodnych jednostronnych oraz dla pochodnych niewłaściwych, o ile nie występują symbole nieoznaczone.
Twierdzenie (o pochodnej funkcji złożonej).
Jeśli funkcja ![]()
jest różniczkowalna w punkcie ![]()
, zaś funkcja ![]()
jest różniczkowalna w punkcie ![]()
to funkcja ![]()
jest różniczkowalna w punkcie ![]()
przy czym [Author ID0: at Tue Aug 14 13:19:00 2001
][Author ID0: at Tue Aug 14 13:19:00 2001
]![]()
[Author ID0: at Tue Aug 14 13:19:00 2001
].
Twierdzenie (o pochodnej funkcji odwrotnej)
Niech U będzie dowolnym podzbiorem otoczenia punktu ![]()
oraz f dowolną funkcją taką, że![]()
. Jeśli ![]()
jest ciągłą i różnowartościową funkcją różniczkowalną w punkcie ![]()
, taką, że ![]()
, to funkcja odwrotna ![]()
jest różniczkowalna w punkcie ![]()
i ![]()
.
Uwaga. Twierdzenia o pochodnej funkcji złożonej i pochodnej funkcji odwrotnej są prawdziwe również dla pochodnych jednostronnych i dla pochodnych niewłaściwych, o ile nie występują symbole nieoznaczone.
Wzory na pochodne funkcji elementarnych
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Definicja różniczki .
Niech funkcja f będzie różniczkowalna w punkcie ![]()
. Różniczką funkcji f w punkcie ![]()
nazywamy funkcję liniową, która dowolnej liczbie rzeczywistej ![]()
przypisuje liczbę ![]()
. Różniczkę funkcji f w punkcie ![]()
będziemy oznaczać jako ![]()
.
Uwaga. Zauważmy, że różniczka funkcji identycznościowej obliczana w dowolnym punkcie przypisuje dowolnej liczbie rzeczywistej ![]()
nią samą. Stąd wniosek, że ![]()
. Ponieważ różniczka funkcji f w dowolnym punkcie ![]()
to ![]()
, więc możemy zapisać, że ![]()
. W powyższym wzorze ![]()
jest funkcją, ![]()
jest funkcją, a ![]()
jest liczbą. Wzór ten można zapisać w postaci ![]()
. Jest on oczywiście prawdziwy dla dowolnego argumentu ![]()
i stwierdza, że iloraz dwóch różniczek jest funkcją stałą. Argument ![]()
z przyczyn praktycznych w powyższym wzorze nie występuje.
Definicja pochodnej rzędu n (indukcja).
Załóżmy, że ![]()
wraz z pewnym otoczeniem, oraz że zdefiniowaliśmy już pochodną ![]()
funkcji ![]()
rzędu ![]()
w każdym punkcie wspomnianego otoczenia. Jeśli ![]()
jest funkcją różniczkowalną w punkcie ![]()
to jej pochodną w tym punkcie nazywać będziemy pochodną rzędu ![]()
funkcji ![]()
w punkcie ![]()
. Pochodną rzędu ![]()
funkcji ![]()
w punkcie ![]()
oznaczać będziemy jako ![]()
. Przyjmujemy ponadto, że ![]()
.
Twierdzenie
Jeżeli f i g mają pochodne rzędu ![]()
w punkcie ![]()
, to funkcja ![]()
ma pochodną rzędu n w punkcie ![]()
i wyraża się ona wzorem
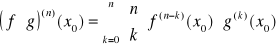
(wzór Leibniza).
Załóżmy, że ![]()
.
TWIERDZENIA O WARTOŚCI ŚREDNIEJ:
Twierdzenie (ROLLE'A)
Jeżeli funkcja f jest ciągła w przedziale [Author ID0: at Tue Aug 14 14:56:00 2001
][Author ID0: at Tue Aug 14 14:56:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:56:00 2001
], różniczkowalna w przedziale [Author ID0: at Tue Aug 14 14:57:00 2001
][Author ID0: at Tue Aug 14 14:57:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:57:00 2001
], oraz [Author ID0: at Tue Aug 14 14:58:00 2001
][Author ID0: at Tue Aug 14 14:58:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:58:00 2001
], to istnieje przynajmniej jeden punkt [Author ID0: at Tue Aug 14 14:59:00 2001
][Author ID0: at Tue Aug 14 14:59:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:59:00 2001
] taki, że ![]()
.
Twierdzenie (CAUCHE'EGO )
Jeżeli funkcje ![]()
i ![]()
są ciągłe w przedziale [Author ID0: at Tue Aug 14 14:56:00 2001
][Author ID0: at Tue Aug 14 14:56:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:56:00 2001
], różniczkowalne w przedziale [Author ID0: at Tue Aug 14 14:57:00 2001
][Author ID0: at Tue Aug 14 14:57:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:57:00 2001
] to istnieje przynajmniej jeden punkt [Author ID0: at Tue Aug 14 14:59:00 2001
][Author ID0: at Tue Aug 14 14:59:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:59:00 2001
] taki, że![]()
.
Twierdzenie (LAGRANGEA).
Jeżeli funkcja f jest ciągła w przedziale [Author ID0: at Tue Aug 14 14:56:00 2001
][Author ID0: at Tue Aug 14 14:56:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:56:00 2001
]i różniczkowalna w przedziale [Author ID0: at Tue Aug 14 14:57:00 2001
][Author ID0: at Tue Aug 14 14:57:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:57:00 2001
], to istnieje punkt [Author ID0: at Tue Aug 14 14:59:00 2001
][Author ID0: at Tue Aug 14 14:59:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:59:00 2001
] taki, że ![]()
.
Powyższe trzy twierdzenia zwane są twierdzeniami o wartości średniej.
Twierdzenie.(warunki dostateczne monotoniczności funkcji)
Niech funkcja ![]()
będzie różniczkowalna w przedziale [Author ID0: at Tue Aug 14 14:56:00 2001
][Author ID0: at Tue Aug 14 14:56:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:56:00 2001
].
Jeśli
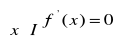
to funkcja f jest stała w przedziale I.Jeśli
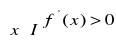
to funkcja f jest rosnąca w przedziale I.Jeśli
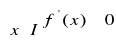
to funkcja f jest niemalejąca w przedziale I.Jeśli
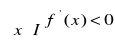
to funkcja f jest malejąca w przedziale I.Jeśli
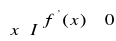
to funkcja f jest nierosnąca w przedziale I.
Twierdzenie.
Jeżeli funkcja ![]()
jest różniczkowalna w przedziale I oraz jest niemalejąca w tym przedziale, to![]()
.
Twierdzenie.
Jeżeli funkcja ![]()
jest różniczkowalna w przedziale I, to jest ona rosnąca w tym przedziale, wtedy i tylko wtedy, gdy ![]()
oraz zbiór ![]()
nie zawiera przedziału.
Twierdzenie.
Niech ![]()
, ![]()
będą funkcjami różniczkowalnymi na przedziale I oraz niech ![]()
. Jeżeli ![]()
oraz ![]()
, to ![]()
.
Twierdzenie. (REGUŁA DE L'HOSPITALA)
Niech ![]()
i ![]()
będą funkcjami różniczkowalnymi w pewnym sąsiedztwie ![]()
punktu ![]()
oraz![]()
. Jeżeli ![]()
, oraz istnieje granica 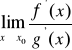
(właściwa lub nie), to istnieje również granica ![]()
przy czym 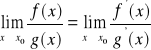
.
Uwaga: twierdzenie odwrotne nie jest prawdziwe.
Twierdzenie (WZÓR TAYLORA)
Jeśli funkcja f ma ciągłą pochodną rzędu ![]()
w przedziale ![]()
oraz pochodną rzędu ![]()
w przedziale ![]()
, to istnieje punkt ![]()
taki, że ![]()
. Ostatni składnik sumy występującej w powyższym wzorze oznaczać będziemy jako![]()
i nazywać resztą w postaci Lagrange'a. Tak więc ![]()
Definicja.
Funkcja f osiąga w punkcie ![]()
maksimum (minimum) lokalne, jeżeli ![]()
(![]()
).
Definicja.
Funkcja f osiąga w punkcie ![]()
maksimum (minimum) lokalne właściwe, jeżeli ![]()
(![]()
).
Maksima i minima funkcji nazywamy ekstremami tej funkcji.
Twierdzenie Fermata. (warunek konieczny istnienia ekstremum).
Jeżeli funkcja f ma ekstremum lokalne w punkcie ![]()
oraz jest różniczkowalna w tym punkcie, to ![]()
.
Twierdzenie. ( I warunek wystarczający istnienia ekstremum lokalnego .
Załóżmy, że ![]()
. Przyjmijmy, że![]()
jest ciągła na ![]()
i różniczkowalna na ![]()
. Jeśli ![]()
to ![]()
ma w punkcie ![]()
minimum właściwe. Jeśli ![]()
to ![]()
ma w punkcie ![]()
maksimum właściwe.
Twierdzenie. (II warunek wystarczający).
Jeżeli funkcja f ma pochodną rzędu ![]()
w pewnym otoczeniu punktu![]()
, ciągłą w punkcie ![]()
, oraz ![]()
, ![]()
, to w przypadku gdy n jest liczbą parzystą, funkcja f ma ekstremum lokalne w punkcie ![]()
. Jest to maksimum właściwe, gdy ![]()
, zaś minimum właściwe, gdy ![]()
. Jeśli n jest liczbą nieparzystą, to f nie ma ekstremum lokalnego w punkcie ![]()
.
Definicja ekstremum absolutnego.
Niech ![]()
i niech f będzie funkcją rzeczywistą taka, że ![]()
. Mówimy, że ![]()
osiąga w punkcie ![]()
maksimum (minimum) absolutne na zbiorze A, jeżeli
![]()
Twierdzenie
Niech ![]()
będzie ciągła w przedziale ![]()
i różniczkowalna w ![]()
. Funkcja ![]()
osiąga w tym przedziale swoje ekstrema absolutne w punktach zbioru ![]()
Definicja.
Załóżmy, że ![]()
jest funkcją różniczkowalną w punkcie![]()
. Funkcję ![]()
nazywamy wypukłą (wklęsłą) w punkcie ![]()
jeśli ![]()
(![]()
). Funkcję ![]()
nazywamy wypukłą (wklęsłą) na przedziale ![]()
, gdy jest wypukła (wklęsła) w każdym punkcie tego przedziału.
Twierdzenie (warunek wystarczający wypukłości (wklęsłości))
Załóżmy, że istnieje druga pochodna funkcji ![]()
w przedziale ![]()
. Jeśli ![]()
(![]()
) to funkcja ![]()
jest wypukła (wklęsła) na ![]()
.
Definicja punktu przegięcia
Mówimy, że funkcja![]()
ciągła w punkcie ![]()
ma w punkcie ![]()
punkt przegięcia, jeśli funkcja ta jest wypukła (wklęsła) na pewnym lewostronnym sąsiedztwie punktu ![]()
i wklęsła (wypukła) na pewnym prawostronnym sąsiedztwie punktu ![]()
.
Twierdzenie (warunek konieczny istnienia punktu przegięcia )
Jeśli funkcja ![]()
ma pochodną rzędu drugiego w pewnym otoczeniu punktu ![]()
ciągłą w ![]()
i ![]()
jest punktem przegięcia funkcji ![]()
to ![]()
.
Twierdzenie ( I warunek wystarczający istnienia punktu przegięcia).
Załóżmy, że ![]()
. Przyjmijmy, że![]()
ma pochodną rzędu pierwszego na ![]()
i pochodną rzędu drugiego na ![]()
. Jeśli ![]()
lub ![]()
to ![]()
ma w punkcie ![]()
punkt przegięcia.
Twierdzenie. (II warunek wystarczający istnienia punktu przegięcia
Jeżeli funkcja f ma pochodną rzędu ![]()
w pewnym otoczeniu punktu![]()
, ciągłą w punkcie ![]()
, oraz ![]()
, ![]()
, to w przypadku gdy n jest liczbą nieparzystą, funkcja f ma w punkcie ![]()
punkt przegięcia.. Jeśli n jest liczbą parzystą, to f nie ma punktu przegięcia w punkcie ![]()
.
Definicja asymptoty pionowej
Załóżmy, że ![]()
jest funkcją określoną na pewnym sąsiedztwie punktu![]()
. Prostą o równaniu ![]()
nazywamy asymptotą pionową funkcji ![]()
gdy ![]()
.
Definicja asymptoty poziomej
Załóżmy, że ![]()
jest funkcją określoną na pewnym przedziale ![]()
. Prostą o równaniu ![]()
nazywamy asymptotą ukośną w minus nieskończoności (plus nieskończoności) funkcji ![]()
gdy ![]()
(![]()
).
Twierdzenie o współczynnikach asymptoty ukośnej
Prosta o równaniu ![]()
jest asymptotą ukośną funkcji ![]()
w minus nieskończoności (plus nieskończoności) wtedy i tylko wtedy gdy ![]()
(![]()
Wyszukiwarka