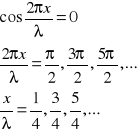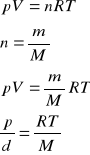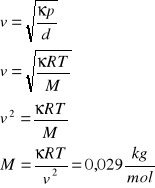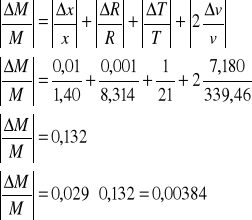Wstęp teoretyczny
Interferencja fal. Wyprowadzenie i dyskusja równania fali wypadkowej.
Interferencją nazywamy zjawisko nakładania się dwu lub więcej fal o tych samych częstotliwościach i amplitudach, różniących się fazami. Różnica faz powinna być stała w dostatecznie długim okresie czasu. Różnica faz takich fal występuje na przykład w skutek różnicy przebytych dróg. Równania falowe dla takich fal są następujące:
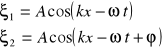
W danym punkcie w przestrzeni fale te wywołują drgania równoległe o różnicy faz ![]()
Wyprowadzenie równania fali wypadkowej
-korzystanie ze wzoru
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Fala wypadkowa ma więc tę pulsację ale inną amplitudę równą ![]()
. Gdy fazy fal są zgodne ![]()
to amplituda fali wypadkowej wynosi 2A, mówimy wówczas, że fale się wzmacniają. Gdy fazy fal są przeciwne ![]()
to amplituda fali wypadkowej jest równa zeru. Mówimy wówczas, że fale się wygaszają.
Warunkiem koniecznym występowania interferencji fal jest to, aby różnica faz fal nakładających się była stała w czasie. Takie fale noszą nazwę spójnych.
.
Fale stojące. Równanie fali stojącej.
Fale stojące powstają wtedy, gdy spotykają się dwa ciągi fal, które mają te same częstotliwości i amplitudy, lecz rozchodzą się w przeciwnych kierunkach. Dzieje się tak często, gdy fala rozchodząc się w ośrodku ograniczonym napotyka na falę odbitą od granicy ośrodka bez straty energii rozchodząc się w kierunku przeciwnym.
W przypadku odbicia od ośrodka akustycznie gęstszego:
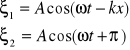
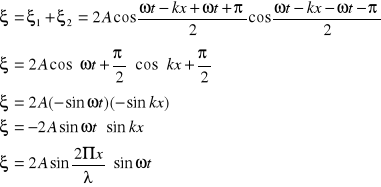
Dla punktów o maksymalnej amplitudzie (strzałek): B=2A
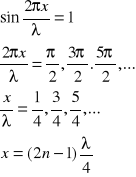
Dla punktów o minimalnej amplitudzie (węzłów): B=0
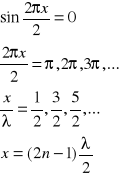
W przypadku odbicia od ośrodka akustycznie rzadszego:
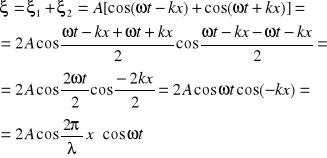
Dla punktów o maksymalnej amplitudzie (strzałek): B=2A
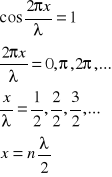
Dla punktów o minimalnej amplitudzie (węzłów): B=0
|
|
Prędkość rozchodzenia się fal w ośrodkach sprężystych. Wyprowadzić wzór Newtona.
Rozchodzenie się fali w długim sprężystym pręcie o przekroju poprzecznym S. Niech działanie siły F w czasie ![]()
t powoduje przesunięcie przekroju S o odległość ![]()
l. W tym samym czasie wywołane działaniem siły rozchodzi się w pręcie na odległość l . zgodnie z drugą zasadą Nevtona musi być spełnione równanie:
![]()
![]()
v
F
l
Załóżmy, że wywołane działaniem siły odkształcenie pręta zawarte jest w granicach proporcjonalności czyli zakładamy , że spełnione są warunki , w których obowiązuje prawo Hooke'a. Podstawiając zamiast naprężenia p stosunek F/S mamy :
![]()
E- moduł Yanga
Masa cząstek objętych zaburzeniem iloczynom objętości Sl i gęstości materiału ![]()
![]()
m = S l![]()
Zmiana prędkości cząstek pręta pozostających pierwotnie w spoczynku, a następnie przesuniętych w czasie ![]()
t odległość ![]()
l wynosi :
![]()
podstawiając do wzoru ![]()
otrzymujemy
![]()
stosunek l / ![]()
t wyraża prędkość rozchodzenia się zaburzenia . Oznaczamy ją symbolem v
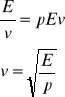
- wzór NEVTONA
Ze wzoru wynika , że prędkość rozchodzenia się fali w pręcie jest proporcjonalna do pierwiastka kwadratowego z modułu Yanga i odwrotnie proporcjonalna do pierwiastka kwadratowego z gęstości.
Jeśli działanie siły wywołuje nie zmiany długości pręta lecz, odkształcenie objętościowe lub postaciowe , to prędkość fali wyraża się wzorami:
![]()
k - moduł sprężystości objętościowej
G - moduł sprężystości postaciowej
W przypadku rozchodzenia się fal sprężystych (objętościowych) w wodzie ![]()
a więc v =1432 m/s
Przy badaniu prędkości rozchodzenia się fal sprężystych w ośrodkach gazowych należy uwzględnić rodzaj zachodzącej przemiany: czy jest to przemiana izotermiczna , tj: zachodzi w stałej temperaturze, czy też jest adiabatyczna, to jest odbywa się bez wymiany ciepła z otoczeniem. W pierwszym przypadku obowiązuje prawo Boyle'a - Moniotte'a pV=const, w drugim prawo Poissona ![]()
Podczas przemian izotermicznych wartość modułu sprężystości objętościowej gazu równa się wartości ciśnienia k = p . Możemy wykazać , że w przemianach adiabatycznych k = Hp , gdzie ![]()
. W tym celu różniczkujemy równanie Poissona ![]()
i otrzymujemy
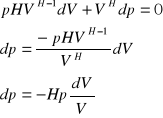
Znak minus przypomina , że wzrostowi ciśnienia odpowiada zmniejszenie się objętości gazu. Porównując ostatnie wyrażenie z prawem Hooke'a ![]()
Znajdujemy, że k=Hp
Rozchodzenie się fali głosowej w gazach odpowiada w przybliżeniu przemianom adiabatycznym. Wyznaczone doświadczalnie wartości prędkości rozchodzenia się fali głosowej w powietrzu zgodne są z wartościami obliczeniowymi ze wzoru ![]()
Równanie stanu gazu doskonałego. Masa molowa (cząsteczkowa).
Dla dostatecznie małych gęstości przy danej masie gazu utrzymywanego w stałej temperaturze jego ciśnienie jest odwrotnie proporcjonalne do objętości (prawo Boyle'a) i przy danej masie gazu utrzymywanego pod stałym ciśnieniem objętość jest wprost proporcjonalna do temperatury (prawo Charlesa i Gay-Lucassa).
Możemy podsumować te wnioski zapisując zależność:
Objętość zajmowana przez jego gaz jest przy stałym ciśnieniu i temperaturze proporcjonalna do jego masy.
Zamiast wyrażenia const w równaniu zapiszemy stałą nR, gdzie n - liczba moli gazu, a R - stała gazowa = 8,314 J/ mol K określana na podstawie doświadczeń, i otrzymujemy
pV=nRT, n=m/M
M - masa molowa, równa względnej masie atomowej
Równanie to nazywamy równaniem stanu gazu doskonałego lub r. Clapeyrona.
Budowa i zasada działania interferometru Quincke'go.
C D
B
A
Interferometr Quincke'go zbudowany jest z dwóch części (rur) zgiętych w kształt litery U tak, że ramiona jednej można wsuwać do ramion drugiej, zmieniając w ten sposób długość ramienia. Przez pomiar przesunięcia ruchomej części można łatwo wyznaczyć długość fali (odczytując kolejne maksima i minima).
Fala głosowa od wlotu A do punktu wyjścia D rozchodzi się dwoma drogami B i C. Ramię C może zmieniać swoją długość podobnie jak w puzonie. Dzięki takiej budowie fala w rurze D powstaje w wyniku nakładania się (interferencji ) dwóch fal cząstkowych biegnących ramionami B i C. Jeżeli długość dróg ![]()
, w ramionach B i C różni się o parzystą liczbę połówek fal, wtedy w ramieniu D obydwie fale wzmacniają się. Gdy różnica ta jest równa nieparzystej liczbie półfal, następuje wygaszenie fali w rurze D. Zmieniając długość ramienia C możemy uzyskać kolejne minima i maksima natężenia dźwięku w rurze D.
Obliczenia
Tabela pomiarów i wyniki
Rachunek błędów
błąd względny
błąd bezwzględny jest mianowany
Obliczam kolejne wartości
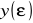
ze wzoru:
Temperatura powietrza |
21oC |
294oK |
|||||
L.p. |
ν [kHz] |
rmax [mm] |
Δrmax [mm] |
rmin [mm] |
Δrmin [mm] |
λ [m] |
V [m/s] |
|
2,5 |
43 |
69 |
18 |
69 |
0,138 |
345 |
1 |
|
112 |
|
83 |
|
|
|
|
2,7 |
51 |
64 |
15 |
64 |
0,128 |
345,6 |
2 |
|
115 |
|
79 |
|
|
|
|
3,0 |
40 |
58 |
13 |
58 |
0,116 |
348 |
3 |
|
98 |
|
71 |
|
|
|
|
3,3 |
35 |
52 |
7 |
52 |
0,104 |
343,2 |
4 |
|
87 |
|
59 |
|
|
|
|
3,5 |
38 |
48 |
7 |
48 |
0,96 |
336 |
5 |
|
86 |
|
55 |
|
|
|
|
3,8 |
29 |
43 |
8 |
43 |
0,86 |
326,8 |
6 |
|
74 |
|
51 |
|
|
|
|
4,0 |
34 |
43 |
0 |
43 |
0,86 |
344 |
7 |
|
77 |
|
43 |
|
|
|
|
4,3 |
22 |
39 |
1 |
40 |
0,795 |
341,8 |
8 |
|
61 |
|
41 |
|
|
|
|
4,5 |
33 |
37 |
4 |
37 |
0,74 |
333 |
9 |
|
70 |
|
41 |
|
|
|
|
4,6 |
22 |
36 |
4 |
36 |
0,72 |
331,2 |
10 |
|
58 |
|
40 |
|
|
|
|
|
Średnia prędkość dźwięku w powietrzu [m/s] |
339,46 |
||||
|
|
Średnia masa cząsteczkowa powietrza [kg/kmol] |
0,029 |
||||
W tabeli pomiarów, w kolumnach Δrmax i Δrmin podałem już uśrednione wartości.
Długość fali λ obliczyłem ze wzoru ![]()
, ![]()
.
Prędkość fali dźwiękowej obliczałem z zależności ![]()
, ![]()
.
Średnią prędkość dźwięku w powietrzu obliczyłem ze wzoru ![]()
, i otrzymałem:
<v>=339,46 m/s
Aby obliczyć średnią masę cząsteczkową powietrza musiałem znaleźć zależność łączącą masę cząsteczkową powietrza, prędkość dźwięku w powietrzu i temperaturę:
κ = 1,40 R = 8,314 J/mol*K T = 21oC = 294oK V = 339,46 m/s |
|
|
Błąd pomiaru prędkości dźwięku obliczyłem metodą Gaussa, czyli metodą średniego błędu kwadratowego.
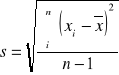
W tym przypadku wzór przyjmuje postać:
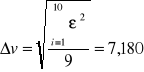
A zatem
![]()
Błąd wyznaczenia średniej masy cząsteczkowej powietrza obliczyłem metodą pochodnej logarytmicznej.
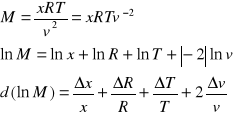
|
|
4 Błąd pomiaru prędkości dźwięku metodą Gaussa:
1 Obliczam ![]()
ze wzoru:
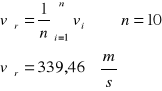
2 Odliczam ![]()
Wynik zawiera tabela załączona do sprawozdania.
3 Obliczam ![]()
Wynik zawiera tabela załączona do sprawozdania.
4 Sumuję poszczególne ![]()
![]()
5 Wyliczam średnie odchylenie od wzoru:
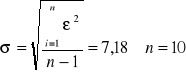
6 Obliczam stałą h ze wzoru:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wnioski
Po wykonaniu ćwiczenia średnia prędkość dźwięku wyniosła 339,46 m/s, a średnia masa cząsteczkowa 0,029 kg/kmol. Zmierzona prędkość odbiega od faktycznej prędkości dźwięku w powietrzu. Spowodowane to może być błędem pomiarowym wynikającym z klasy urządzenia pomiarowego. Stwierdzam, że gdyby przeprowadzić więcej pomiarów zmierzona prędkość byłaby dokładniejsza.
1
2
![]()
Wyszukiwarka