Nr. Ćwicz. 220 |
data 20-05-1999 |
Andrzej Gessner |
WBMiZ |
Semestr: IV |
grupa : M1 |
Prowadzący: dr Arkadiusz Ptak |
|
|
Przygotowanie: |
Wykonanie: |
ocena ostatecz.: |
TEMAT: WYZNACZANIE STAŁEJ PLANCKA I PRACY WYJŚCIA NA PODSTAWIE ZJAWISKA FOTOELEKTRYCZNEGO
1. Wstęp:
W ciałach stałych będących przewodnikami, elektrony walencyjne nie są związane z macierzystymi atomami - poruszają się one swobodnie w sieci krystalicznej tworząc tzw. gaz elektronowy. W wyniku wzajemnego oddziaływania atomów bariery potencjału oddzielające sąsiednie atomy ulegają obniżeniu do wartości mniejszej niż całkowita energia elektronu i nie stanowią przeszkody w ruchu elektronów.
Atomy znajdujące się na powierzchni kryształu mają sąsiadów tylko od strony wnętrza i dlatego energia potencjalna w pobliżu tych atomów jest inna niż w głębi kryształu. Energia potencjalna na powierzchni jest większa, więc powierzchnia stanowi barierę dla elektronów, dzięki której nie mogą one opuścić kryształu. Opuszczenie metalu przez elektron (pokonanie bariery potencjału Uo) jest możliwe, jeśli uzyska on na to dodatkową energię o wartości przynajmniej e*Uo. Ta energia nazywa się pracą wyjścia. Źródłem energii mogą być:
a) podwyższona temperatura - termoemisja
b) silne pole elektryczne - emisja polowa
c) bombardowanie cząstkami o dostatecznie dużej energii kinetycznej
d) oświetlenie kryształu
W przypadku oświetlenia kryształu mamy doczynienia ze zjawiskiem fotoelektrycznym.
Wybicie elektronu z metalu przez foton zachodzi tylko wtedy, gdy energia fotonu hυ jest równa lub większa od pracy wyjścia W.
Przemiany energii w zjawisku fotoelektrycznym opisuje równania Einsteina
(1)
gdzie: h - stała Plancka równa 6,62⋅10 -34 J⋅s, υ - częstotliwość fali świetlnej, W - praca wyjścia
m - masa elektronu, v - jego prędkość poza metalem.
Prąd fotoelektryczny płynie nawet wtedy, gdy między anodą i katodą nie ma napięcia. Dzieje się tak dzięki energii kinetycznej posiadanej przez elektrony w momencie wybicia z metalu. Całkowity zanik prądu można spowodować przykładając napięcie o przeciwnej polaryzacji, tzn. potencjał niższy na anodę. Jeżeli napięcie ma odpowiednią wartość zwaną potencjałem hamującym Vh to następuje całkowite zahamowanie elektronów - ich energia kinetyczna zostaje zużyta na wykonanie pracy przeciwko polu elektrycznemu.
(2)
Uwzględniając powyższy związek możemy przekształcić równanie (1) do postaci :
(3)
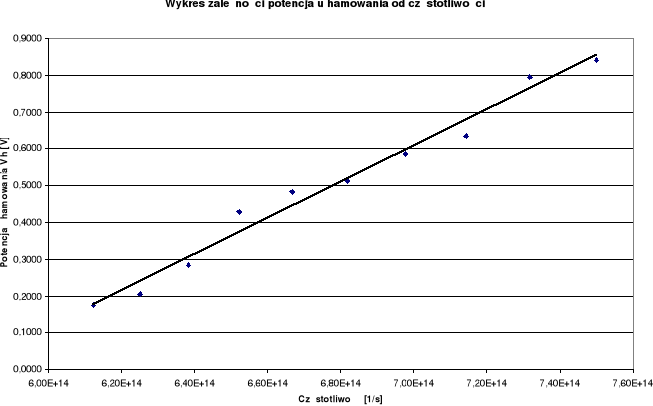
Na podstawie wykresu zależności Vh=f(υ) można znaleźć stałą Plancka h oraz pracę wyjścia W, gdyż tangens kąta nachylenia prostej opisanej równaniem (3) wynosi h/e, a punkt przecięcia prostej z osią rzędnych ma wartość - W/e.
nr. filtru |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
λ [nm] |
400 |
410 |
420 |
430 |
440 |
450 |
460 |
470 |
480 |
490 |
Pomiary i obliczenia:
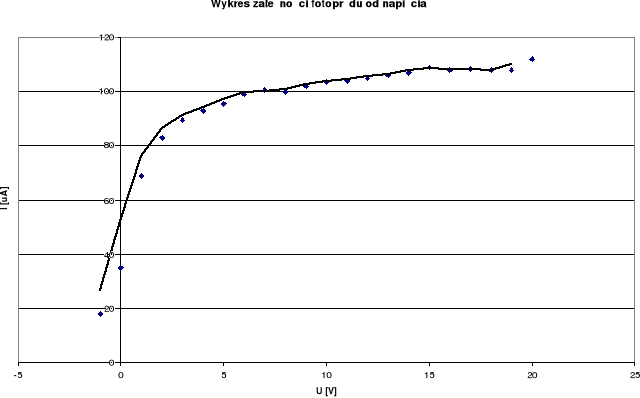
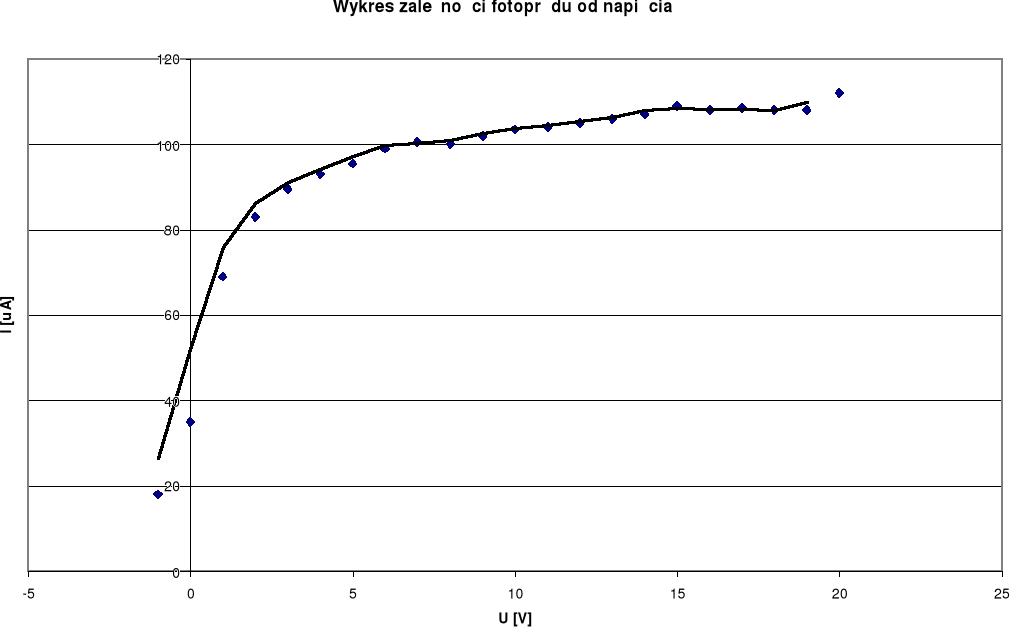
Tabelka z pomiarami fotoprądu w zależności od napięcia:
U [V] |
I [μA] |
||
|
1 |
2 |
śr |
+20,00 |
113 |
111 |
112 |
+19,00 |
109 |
107 |
108 |
+18,00 |
108 |
108 |
108 |
+17,00 |
109 |
108 |
109 |
+16,00 |
108 |
108 |
108 |
+15,00 |
110 |
108 |
109 |
+14,00 |
107 |
107 |
107 |
+13,00 |
106 |
106 |
106 |
+12,00 |
106 |
104 |
105 |
+11,01 |
105 |
103 |
104 |
+10,00 |
104 |
103 |
104 |
+9,01 |
102 |
102 |
102 |
+8,01 |
101 |
99 |
100 |
+7,00 |
103 |
98 |
101 |
+6,00 |
102 |
96 |
99 |
+5,00 |
98 |
93 |
96 |
+4,00 |
94 |
92 |
93 |
+3,00 |
91 |
88 |
90 |
+2,00 |
84 |
82 |
83 |
+1,00 |
70 |
68 |
69 |
0,00 |
35 |
35 |
35 |
-1,00 |
18 |
18 |
18 |
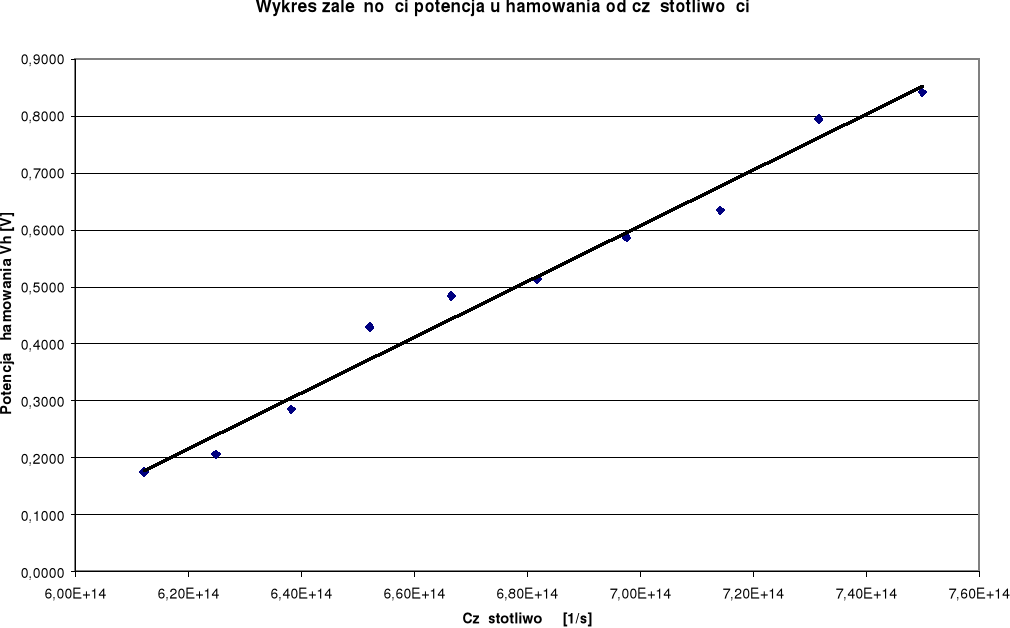
Pomiary napięcia hamowania:
Nr filtru |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Vh [V] |
1 |
-0,8321 |
-0,7896 |
-0,6326 |
-0,5866 |
-0,5128 |
-0,4838 |
-0,4255 |
-0,2865 |
-0,1971 |
-0,1760 |
|
2 |
-0,8483 |
-0,7959 |
-0,6353 |
-0,5864 |
-0,5129 |
-0,4828 |
-0,4351 |
-0,2843 |
-0,2148 |
-0,1738 |
|
3 |
-0,8433 |
-0,7983 |
-0,6345 |
-0,5861 |
-0,5127 |
-0,4848 |
-0,4255 |
-0,2820 |
-0,2041 |
-0,1741 |
|
śr |
-0,8412 |
-0,7946 |
-0,6341 |
-0,5864 |
-0,5128 |
-0,4838 |
-0,4287 |
-0,2843 |
-0,2053 |
-0,1746 |
Wyznaczanie stałej Plancka i pracy wyjścia:
Równanie prostej regresji z wykresu zależności potencjału hamowania od częstotliwości:
y = 5·10-15x - 2,8253, Δa = 2,623·10-16 [J·s/C], Δb = 0,165 [J/C]
Korzystając z zależności:
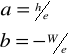
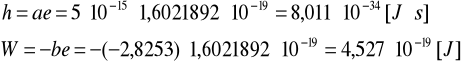
obliczamy stałą Plancka h oraz pracę wyjścia W:
Obliczenia błędów:
Dokładność pomiarów:
ΔU = 0,01 [V]
ΔI = 1 [μA]
ΔVh = 0,0001 [V]
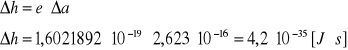
Błąd wyznaczenia stałej Plancka h metodą różniczki zupełnej wyznaczony został ze wzoru:
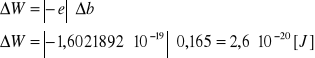
Błąd wyznaczenia pracy wyjścia W -metodą różniczki zupełnej ze wzoru:
Zestawienie wyników:
Stała Plancka:
wartość tablicowa: h = 6,62·10-34 [J·s]
wartość wyznaczona doświadczalnie: h = (8,01 ± 0,42)·10-34 [J·s]
Praca wyjścia:
W = (4,53 ± 0,26)·10-19 [J]
Wnioski:
Zależność fotoprądu od napięcia nie jest zależnością liniową. Dla wartości bliskich 0V natężenie wzrasta gwałtownie, powyżej 4V notuje się spadek wzrostu i dalej funkcja rośnie już w mniejszym stopniu. Zależność potencjału hamowania od częstotliwości fali świetlnej jest liniowa, jak można odczytać na dołączonym wykresie. Pewien rozrzut wartości dokoła prostej regresji jest wynikiem niestabilnej pracy miernika. Obliczona wartość stałej Plancka różni się w znacznym stopniu od wartości tablicowej. Rozbieżność tą można tłumaczyć niestabilnymi wskazaniami mierników.
Wykresy:
![]()
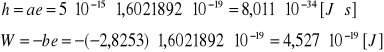
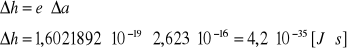
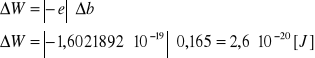
Wyszukiwarka