WALEC

Rozkład materiału - GEOMETRIA

Klasa I	Klasa II	Klasa III
Figury na płaszczyźnie Symetrie Kąty w kole	Długość okręgu. Pole koła Trójkąty Prostokątne Wielokąty i okręgi Wielościany	Powtórzenie wiadomości Figury podobne Stereometria

Analizowane podręczniki:

1. Matematyka z plusem. Podręcznik dla klasy 3. Praca zbiorowa pod redakcją Małgorzaty Dobrowolskiej, Gdańskie Wydawnictwo Oświatowe, Gdańsk 2001

2. Józef Dawid, Ewa Rucińska, Wojciech Jędrychowski, Matematyka 2001. Gimnazjum. Podręcznik dla klasy 3, Wydawnictwo Szkolne i Pedagogiczne, Warszawa 2001

3. Anna Drężek, Barbara Grabowska, Matematyka wokół nas. Podręcznik dla klasy 3, Wydawnictwo Szkolne i Pedagogiczne, Warszawa 2001

I. Zagadnienie dotyczące Walca po raz pierwszy pojawia się w klasie III gimnazjum w rozdziale dotyczącym „Stereometrii”. W podręczniku „Matematyka z plusem” wprowadzone jest ona w rozdziale zatytułowanym „Bryły”, który dzieli się na kolejne podrozdziały: 1.Graniastosłupy 2.Ostrosłupy 3.Przykłady brył obrotowych 4.Walec 5.Stożek 6.Kula 7.Zadania uzupełniające. W „Matematyce 2001” rozdziały, w których znajdziemy to zagadnienie to: „Bryły obrotowe” oraz „Pola i objętości brył obrotowych”. Natomiast w „Matematyce wokół nas” temat ten zawarty jest w rozdziale „Bryły obrotowe” i również podzielony jest na kilka podrozdziałów: 1.Przykłady brył obrotowych 2.Walec 3.Stożek 4.Kula 5.Pola powierzchni brył obrotowych 6.Objetości brył obrotowych 7.Zadania utrwalające 8.Sprawdź, czy to umiesz.

Wprowadzenie pojęcia walca wymaga od uczniów dobrej znajomości figur płaskich oraz pojęć związanych z bryłami takich jak: podstawa, promień podstawy czy wysokość, siatka bryły, przekątna bryły, uczniowie muszą znać również wzory na wyliczanie pół i objętości brył. Poznając bryły obrotowe uczniowie poznają również związane z nimi pojęcia, np. oś obrotu, przekrój osiowy i przekrój poprzeczny.

II. Sposoby wprowadzania.

Podręcznik „Matematyka z plusem” proponuje wprowadzenie zagadnienia Brył obrotowych z wykorzystaniem pomocy w postaci wiertarki i kartonika, bądź zwykłego ołówka i kartonu. W wyniku obrotu wiertła lub ołówka z kartonikiem w kształcie figury płaskiej, można dostrzec powstające bryły, zwane bryłami obrotowymi. „Matematyka 2001” i „Matematyka wokół nas” prezentują szereg przykładów, gdzie w życiu codziennym spotykamy bryły obrotowe, są nimi np. puszki czy rury. Zagadnienie dotyczące samego walca, w każdym podręczniku wprowadzone jest w taki sam sposób. Powiedziane jest, że walec otrzymujemy w wyniku obrotu prostokąta dookoła prostej, zawierającej jego bok. „Matematyka wokół nas” jako jedyna dodaje, że jest to obrót o 360⁰. W każdym z podręczników, na początku rozdziału, zaproponowane są zadania, w których uczniowie muszę wykazać się znajomością wyglądu siatki walca, przekroju osiowego czy poprzecznego bryły, umiejętnością zaznaczenia wysokości figury, promienia podstawy czy tworzącej. Jedyne co różni te zadania od siebie, to poziom trudności. Według mnie najprostsze zadania proponuje „Matematyka wokół nas”:

Zad. 1/283

Narysuj walec i zaznacz na rysunku kolorem jego przekrój osiowy. Czym dla walca są boki tego przekroju?

Zad. 7/283

Oblicz pole przekroju osiowego walca, wiedząc, że obwód podstawy jest równy 6Π cm, a wysokość walca jest o 7 cm dłuższa od promienia podstawy.

Najtrudniejsze zaś „Matematyka z plusem”, dla porównania mamy zadania:

Zad. 3/169

Promień podstawy walca ma długość 4 cm, wysokość walca ma 8 cm długości. Oblicz długość przekątnej przekroju osiowego tego walca.

Zad. 4/169

Przekątna przekroju osiowego walca ma długość 12 cm i jest nachylona do podstawy walca pod kątem 60⁰. Oblicz długość promienia i wysokość walca.

W „matematyce wokół nas” podobne zadania, z zastosowaniem funkcji trygonometrycznych i twierdzenia Pitagorasa pojawiają się dopiero przy wyliczaniu pól powierzchni i objętości walców.

We wszystkich podręcznikach wzory na pole powierzchni walca wprowadzane są za pomocą jego siatki, czyli wyjaśnienia, że pole całkowite składa się z sumy pól dwóch podstaw2^. Πr² i pola prostokąta 2ΠrH, wzór na objętość zaś wprowadzany jest zasadzie analogii do graniastosłupa, z tym, że tu pole podstawy stale wyraża się wzorem P_p=Πr², a H to wysokość walca

Objętość walca V=Πr^2.H Pole powierzchni całkowitej walca P_c=2^. Πr² + 2ΠrH

Typowe zadania na wyliczanie pól i objętości pojawiające się w każdym z podręczników:

Zad.

Prostokąt o wymiarach 6 cm x 8 cm obraca się raz dokoła większego boku, drugi raz dokoła mniejszego boku. Oblicz stosunek pól powierzchni powstałych brył.

Zad.

Jakie są objętości walców, które powstały w wyniku obrotu prostokąta o wymiarach 10 cm i 6 cm, gdy osią obrotu dla jednego był dłuższy bok, a dla drugiego krótszy bok.

Porównując ze sobą sposoby w jakie autorzy wprowadzają pojęcie walca i innych brył obrotowych mogę stwierdzić, że najkorzystniej czyni to „Matematyka 2001”. Wszystkie najważniejsze informacje dotyczące brył obrotowych, tj. pola powierzchni czy objętości zestawione są w przejrzystych tabelkach, ułatwiających porównanie tych brył ze sobą i jednocześnie naukę poszczególnych wzorów. „Matematyka wokół nas” jak również „Matematyka z plusem” omawiają te bryły po kolei, rozpoczynając od walca, po czym zajmują się stożkiem, a następnie kulą. Wiąże się to również z zadaniami pojawiającymi się w podręcznikach. W „Matematyce 2001” zadania łączą w sobie wiadomości odnośnie walca, stożka i kuli, co zdecydowanie rzadziej można zaobserwować w dwóch pozostałych podręcznikach.

III. Prawdopodobne problemy i trudności.

Moim zdaniem najpoważniejsze trudności związane z tym zagadnieniem wiążą się z tym, iż na początku, uczniowie muszą bardzo dużo rzeczy sobie wyobrazić. Wszystkie ćwiczenia, wprowadzające do tematu, w podręczniku „Matematyka z plusem” rozpoczynają się od słów: „Wyobraź sobie”, a wiadomo, że nie każdy jest w stanie sobie wszystko wyobrazić, dlatego bardzo ważne jest, aby uczniowie mogli porozcinać te bryły i rozłożyć je na płaszczyźnie, dopiero wówczas nie będą mieli wątpliwości, że obliczając sumę pól otrzymanych figur płaskich, otrzymują pole powierzchni odpowiedniej bryły. Bardzo wiele zadań ułatwiających uczniom zrozumienie tematu znajduje się w książce „Matematyka 2001”, gdzie należy wielokrotnie wyciąć z kartonu prostokąt, obrócić go i dopiero wówczas naszkicować bryłę jaka powstanie, czyli walec. Inne problemy mogłyby się pojawić podczas rozwiązywania zadań tekstowych dotyczących walca, z wykorzystaniem poznanych wcześniej własności trójkątów prostokątnych o kątach 90^o, 45^o, 45^o lub 90^o, 30^o, 60^o oraz twierdzenia Pitagorasa. Wszelkie trudności mogłyby wynikać z wcześniejszego, niedostatecznego opanowania tych treści i nieumiejętności ich wykorzystania w rozwiązywaniu zadań, czyli nie dostrzeżenia pojawiających się w nich zależności.

IV. Wiadomości i umiejętności związane z obliczaniem pól powierzchni walców oraz ich objętości wykorzystywane są podczas realizacji kolejnych tematów z działu dotyczącego brył obrotowych. Szczególnie wyraźnie widać to w momencie wprowadzana wzoru na objętość stożka. Każdy z podręczników wyraźnie podkreśla związek pomiędzy objętością walca a objętością stożka, mianowicie udowadniane jest, że objętość stożka jest trzy razy mniejsza niż objętość walca o takiej samej podstawie i wysokości.

V. Występowanie i postać na egzaminach zewnętrznych - standardy egzaminacyjne

Test gimnazjalny 2004 Standard I.3 - Posługiwanie się własnościami figur

Zadanie 34. (0-5)

Dziecko nasypuje piasek do foremek w kształcie stożka o promieniu podstawy 5 cm

i tworzącej 13 cm. Następnie przesypuje go do wiaderka w kształcie walca o wysokości

36 cm i promieniu dwa razy większym niż promień foremki. Jaką część wiaderka

wypełniło dziecko, wsypując 6 foremek piasku? Zapisz obliczenia.

Rozwiązanie:

• zastosowanie poprawnej metody obliczenia wysokości stożka

• zastosowanie poprawnej metody obliczenia objętości stożka (foremki)

• zastosowanie poprawnej metody obliczenia objętości walca (wiaderka)

• zastosowanie poprawnej metody obliczenia, jaką część wiaderka wypełnił piasek z sześciu foremek

• bezbłędne wykonanie rachunków

Test gimnazjalny 2005 Standard IV.3 - Tworzenie modeli sytuacji problemowej

Zadanie 13. (0-1)

Które z naczyń w kształcie walca, o wymiarach przedstawionych na rysunku, ma

największą objętość?

h - wysokość walca r - promień podstawy walca

I. r = 6 cm II. r = 5 cm III. r = 4 cm IV. r = 3 cm

h = 6 cm h = 9 cm h = 12 cm h = 18 cm

A. I B. II C. III D. IV

Rozwiązanie: Odpowiedź B

Test gimnazjalny 2007 Standard IV.3 - Tworzenie modeli sytuacji problemowej

Zadanie 28. (0-2)

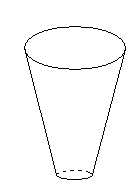
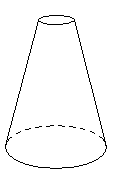
Do początkowo pustych wazonów, takich jak przedstawione na rysunkach, jednakowym

i równomiernym strumieniem wpływała woda.

................... ...................... .........................

Na wykresach I - IV przedstawiono schematycznie charakter zależności wysokości

poziomu wody w wazonie od czasu jego napełniania. Pod każdym wazonem wpisz

numer odpowiedniego wykresu.

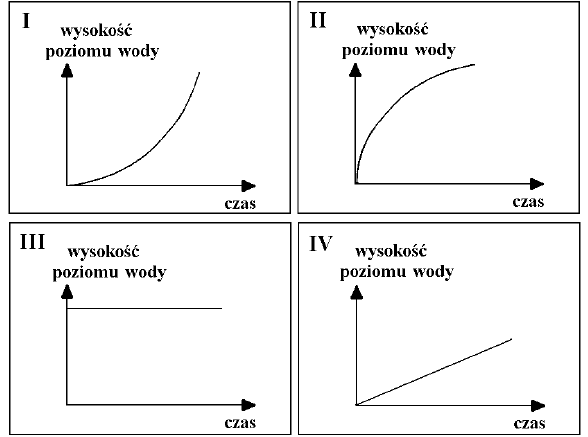
Rozwiązanie: Odpowiedź: II, IV, I

VI. Wykorzystanie zagadnienia podczas realizacji ścieżek międzyprzedmiotowych

Jedną ze ścieżek międzyprzedmiotowych, którą można by zrealizować podczas omawiania zagadnienie walca, jest ścieżka regionalna. Podczas realizacji tej ścieżki można poprosić uczniów, aby wyszukali jak najwięcej budynków w swojej okolicy, które wyglądem przypominają walec, a następnie mogli by odszukać informacje w Internecie, bądź literaturze na temat tego budynku, co pozwoliłoby zrealizować ścieżkę czytelniczą i medialną.

Umiejętność wyliczania pól powierzchni walców i ich objętości mogą być wykorzystywane na lekcjach chemii, gdzie między innymi menzurki mają kształt walca, a uczniowie mogą wyliczać objętość płynów w niej zawartych, na geografii bądź na fizyce, np.:

Zadanie o treści geograficznej

Rurociąg doprowadzający wodę do osiedla ma średnicę wewnętrzną 16 cm. Ile m³ wody zużywa to osiedle w czasie jednej doby, jeżeli średnia szybkość wody w rurociągu wynosi 0,5m/s?

Zadanie o treści fizycznej

Do wykonania uzwojenia pierwotnego transformatora zużyto 100 m drutu miedzianego o średnicy 2 mm. Ile waży miedź zużyta do wykonania tego uzwojenia, jeżeli gęstość miedzi wynosi 8950kg/m³.

VII. Cele operacyjne - WALEC

Temat zajęć	Cele podstawowe	Cele ponadpodstawowe
Walec	zna pojęcie walca rozumie pojęcie walca, wskazuje model umie kreślić siatkę walca oraz wskazać przekroje walca (osiowy i poprzeczny) zna wzór na objętość i pole powierzchni całkowitej walca umie obliczyć pole powierzchni całkowitej lub bocznej walca, podstawiając do wzoru umie obliczyć objętość walca, podstawiając do wzoru umie rozwiązać zadanie tekstowe związane z polem powierzchni całkowitej lub objętością walca	umie rozwiązać zadanie tekstowe związane z polem powierzchni, całkowitej lub objętością walca umie stosować twierdzenie Pitagorasa w zadaniach o walcu umie stosować własności trójkątów prostokątnych o kątach 90^0, 45^0, 45^0oraz 90^0, 30^0, 60^0w zadaniach o walcu umie rozwiązać zadanie tekstowe związane z bryłami złożonymi z walców

VIII. Zadania

Zad.1

Puszka w kształcie walca jest oklejona etykietą z papieru. Jaki kształt ma ta etykieta po przecięciu jej prostopadle do podstawy puszki i rozwinięciu? Jak wygląda siatka walca?

Zad.2

Przekrój osiowy walca jest kwadratem o polu 16 cm². Oblicz pole powierzchni całkowitej i objętość walca.

Zad.3

Przekrój osiowy walca jest prostokątem o boku 12 cm, którego przekątne przecinają się pod kątem 60⁰. Oblicz objętość tego walca.

Zad.4

Kwadrat o boku 12 cm obrócono o kąt, który łączy środki przeciwległych boków. Narysuj w skali 1 : 3 siatkę otrzymanej bryły.

Zad. 5

W walec wpisano graniastosłup prawidłowy trójkątny, a z kolei w graniastosłup wpisano walec. Zatem stosunek objętości walców wynosi:

1. 4 : 1

2. 3 : 1

3. 1 : 2

Zad. 6

Jak zmieni się objętość walca, gdy trzykrotnie zwiększymy długość jego promienia?

1. wzrośnie trzykrotnie

2. wzrośnie dziewięciokrotnie

3. nie zmieni się

Zad. 7

Fabryka produkuje dwa rodzaje blaszanych puszek. Każda puszka ma pojemność 1 l i kształtem przypomina walec. Puszki mają wysokość 20 cm albo 25 cm. Na którą puszkę zużywa się więcej blachy? (na wyższą puszkę)

Zad. 8

Pewna firma sprzedawała sok pomidorowy w puszkach w kształcie walca o promieniu podstawy r i wysokości h. Firma konkurencyjna wypuściła na rynek taki sam sok pomidorowy w puszkach w kształcie walca, którego promień podstawy był większy o 10%, a wysokość mniejsza o 10%. Obaj producenci ustalili jednakową cenę za puszkę soku. Która firma sprzedawała drożej?

Zad. 9

W walec wpisano stożek, a w stożek wpisano kulę, jak na rysunku.

Wiedząc, że przekrój osiowy stożka jest trójkątem

Równobocznym o boku a, spróbuj

wyznaczyć pola powierzchni całkowitych tych brył.

IX. Realizacja zagadnienia - ciekawe metody i środki.

Uczniowie zagadnienia dotyczącego brył obrotowych, w tym walca, najlepiej uczą się poprzez obserwację i manipulację modelami, dlatego można wykorzystać tu środki dydaktyczne w postaci:

• tablic matematycznych dotyczących objętości i pól powierzchni całkowitych danych brył

• brył geometrycznych z siatkami

• brył geometrycznych z przekrojami

oraz metody takie jak:

• prezentacja multimedialna dotycząca siatek brył obrotowych, np. wykonana w programie PowerPoint;

• prezentacja, wykorzystująca między innymi ołówek i kartonik, bądź prostokątną kartkę papieru, uczniowie obserwują wówczas, w jaki sposób powstają bryły obrotowe, tym samym uczą się i potrafią wskazać oś obrotu czy przekrój poprzeczny danej figury;

• dyskusja, pogadanka na temat tego, gdzie w życiu codziennym mamy do czynienia z walcami;

• ćwiczenia, czyli rozwiązywanie zadań o treści z życia codziennego z wykorzystaniem wiadomości o walcu;

X. Konspekt lekcji

Konspekt lekcji.

Magdalena Golon 22.03.2007 r.

III klasa gimnazjum

1. Temat lekcji: Walec - obliczanie pól powierzchni całkowitej i objętości.

2. Cele operacyjne lekcji:

1. Uczeń zna pojęcie walca.

2. Uczeń potrafi kreślić siatkę walca.

3. Uczeń zna wzór na objętość walca oraz potrafi wyliczyć objętość wykorzystując dany wzór.

4. Uczeń zna wzór na pole powierzchni całkowitej walca.

5. Uczeń umie obliczyć pole powierzchni całkowitej lub bocznej wykorzystując podane wzory.

6. Uczeń potrafi rozwiązać zadanie tekstowe związane z polem powierzchni całkowitej lub objętością walca.

3. Środki dydaktyczne:

Tablica, kreda, podręcznik do matematyki, kartki z zadaniami dla uczniów (załącznik nr1)

4. Metody nauczania: pogadanka, wyjaśnienie, ćwiczenia.

Forma pracy: zbiorowa.

5. Przebieg lekcji:

1. Wstępne czynności organizacyjne: przywitanie się z uczniami, sprawdzenie obecności, mobilizacja do pracy, podanie tematu lekcji.

2. Opracowanie części głównej lekcji:

Przypomnienie poznanej wcześniej definicji walca:

Nauczyciel: Jaką bryłę obrotową nazywamy walcem?

Uczniowie: Walcem nazywamy bryłę, którą można otrzymać w wyniku obrotu prostokąta dookoła prostej, zawierającej jego bok.

Nauczyciel: Jak nazywamy prostą wokół, której obracamy dany prostokąt?

Uczniowie: Prostą nazywamy osią obrotu.

Ćwiczenie wprowadzające wzór na pole powierzchni całkowitej walca

Narysuj siatkę walca, wiedząc, że promień podstawy wynosi 2 cm, a wysokość bryły 5 cm.

Dane:

r = 2 cm

h = 5 cm

Nauczyciel: W jaki sposób wyliczylibyście pole powstałej siatki?

Uczniowie: Należy wyliczyć pola dwóch kół oraz pole prostokąta, a później je do siebie dodać.

Obliczenia:

Pole koła P=πr² pole kół, czyli dwóch podstaw walca P=2π2²=8π

Pole prostokąta P=ab pole danego prostokąta, czyli pole powierzchni bocznej P=2πr ^. h P=2π2^.5=20π

A zatem mamy, że pole całkowite walca jest sumą pól jego podstaw i pola powierzchni bocznej.

P=2πr²+2πr ^. h

Zad.1

Prostokąt o wymiarach 6 cm x 8 cm obraca się raz dokoła większego boku, drugi raz dokoła mniejszego boku. Oblicz stosunek pól powierzchni powstałych brył.

Rozwiązanie:

Dane: Szukane:

h₁=8 cm r₁,r₂

h₂=6 cm
=?

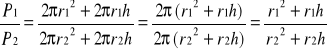
8=2πr₁ r₁=
6=2πr₂ r₂=

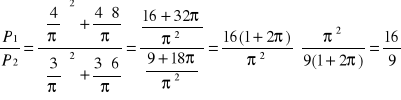
Odp. Stosunek pól powierzchni powstałych walców wynosi
.

Zad.2

Pojemniki, w których przewozi się benzynę, mają kształt walca o wysokości 1 m i promieniu podstawy 40 cm. Ile litrów benzyny mieści się w takim pojemniku? Ile(co najmniej) blachy trzeba zużyć, aby taką beczkę wykonać?

Rozwiązanie:

Przypomnienie wzoru na objętość walca: V= πr^2.h

Dane: Szukane:

h = 1 m V=?

r = 40cm = 0,4 m (ujednolicenie jednostek)

P=?

[m³]

[m²]

1m³=1000l

0,5m³=500l

Odp.W beczce tej mieści się 500l benzyny, a trzeba a nią zużyć co najmniej 3,1 m² blachy.

Zad.3

Przekątna przekroju osiowego walca ma długość 5 cm i nachylona jest do płaszczyzny podstawy pod kątem 60⁰. Jaką długość ma promień podstawy tego walca? Jaka jest wysokość walca?

Rozwiązanie:

Dane: Szukane:

c=5cm r=?

α=60⁰ h=?

Korzystając z funkcji trygonometrycznych mamy:

cosα=
cos60⁰=

2a=5 a=2,5

r=
r=0,5^.2,5=1,25 [cm]

Korzystając z twierdzenia Pitagorasa a²+h²=c² otrzymujemy:

h²=c²-a² h²=5²+2,5²=25+6,25=31,25=31
h=
[cm]

Odp. Wysokość walca wynosi
cm, a promień podstawy 1,25 cm.

Zad. 4

Powierzchnię boczną puszek w kształcie walca oklejona samoprzylepną folią. Oblicz, ile metrów kwadratowych folii należy przygotować na oklejenie 100 puszek, wiedząc, że promień podstawy jest równy ¼ wysokości puszki i ma 5 cm długości.

Rozwiązanie:

Dane:

r = 5cm

r=
h, h = 4r h= 4^.5=20 cm

π=3,14

P_{powierzchni bocznej walca}=2π^.h

P=2^.3,14^.5^.20=628 [cm²]

Zamiana jednostek: 1m²=10 000 cm² 100^.628=62 800 cm²=6,28 m²

Odp. Należy przygotować 6,28 m² folii.

6. Uwagi własne:

Jeśli wystarczy czasu zostanie dodatkowo rozwiązane zadanie:

Czy na kartce papieru o wymiarach 20cm x 14cm zmieści się siatka walca, którego powierzchnia boczna jest prostokątem o polu równym 108cm², a jego dłuższy bok jest trzy razy dłuższy od krótszego boku.

Rozwiązanie:

Dane: Szukane:

P_pow.bocznej=108cm² P=2πr²+2πr ^. h=?

P_pow.bocznej=4a²

108=3a² a=

3a=2πr r=

P=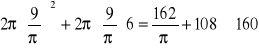
cm²

Pole kartki papieru wynosi 20^.14=280 cm²

Odp. Na kartce papieru zmieści się siatka walca o podanych wymiarach.

To zadanie, jeśli nie zostanie wykonane na lekcji, zostanie zadane jako praca domowa.

Literatura:

• Matematyka z plusem. Podręcznik dla klasy 3. Praca zbiorowa pod redakcją Małgorzaty Dobrowolskiej, Gdańskie Wydawnictwo Oświatowe, Gdańsk 2001

• Józef Dawid, Ewa Rucińska, Wojciech Jędrychowski, Matematyka 2001. Gimnazjum. Podręcznik dla klasy 3, Wydawnictwo Szkolne i Pedagogiczne, Warszawa 2001

• Anna Drężek, Barbara Grabowska, Matematyka wokół nas. Podręcznik dla klasy 3, Wydawnictwo Szkolne i Pedagogiczne, Warszawa 2001

2Πr

r

h

8 cm

6 cm

60⁰

5cm

a

h

2πr

h

3a

a

---