Teoria Mechanizmów

i Maszyn

Analiza kinematyczna i kinetostatyczna mechanizmu suwakowego

Mech-6/A

xxxxxxxxxxxxxx

WIMiR gr. 1x rok II C

Rok akademicki 2010/2011

1. Synteza strukturalna i geometryczna mechanizmu

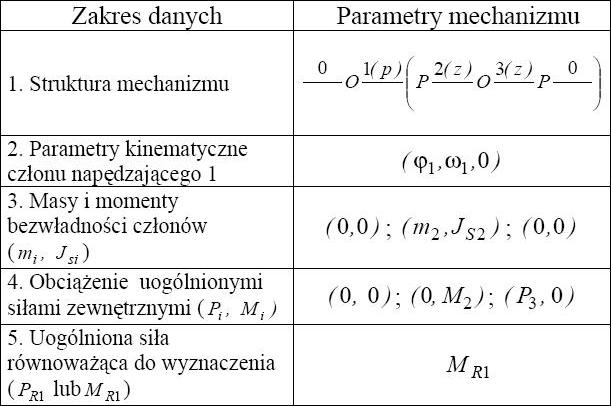
Symboliczny zapis struktury i parametrów projektowanego mechanizmu przedstawia tabela

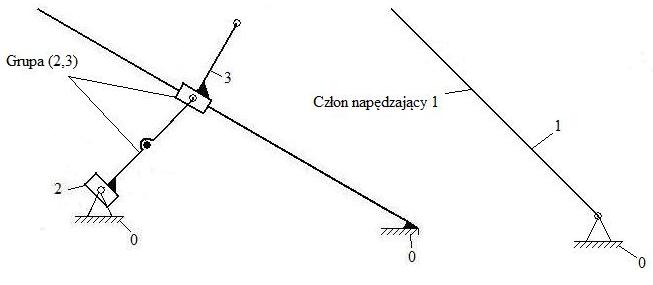
1.1 Budowa łańcucha kinematycznego - schemat ideowy.

Zgodnie z numerem zadania przyjęto wymiary mechanizmu i położenie jak na rysunku.

AB = 0,5m P₃ = 200 N

BS₂ = 0,15m P₃ || CE

BC = 0,3m

CD = 0,2m

CE = 0,6m

φ₁ = 135°

ω₁ = 2

1.2 Ruchliwość i klasa mechanizmu

Ruchliwość mechanizmu

w=3n-p₄-2p₅

liczba członów n = 3; liczba par kinematycznych klasy IV p₄=0; liczba par kinematycznych klasy V p₅=4; (0,1), (1,2), (2,3), (3,0)

Klasa mechanizmu

Po odłączeniu członu napędzającego 1, pozostałe człony tworzą grupę strukturalną.

Badam ruchliwość grupy strukturalnej po połączeniu jej członów ruchomych z podstawą; n=2, p₅=3; (0,2), (2,3), (3,0).

w_gr=3n-2p₅=
=0

Grupa strukturalna (2,3) jest grupą klasy 2, postaci 4.

Analizowany mechanizm składa się z członu napędzającego 1 i grupy strukturalnej klasy 2, jest więc mechanizmem klasy 2.

Nazwa strukturalna mechanizmu: mechanizm suwakowy

2. Analiza kinematyczna mechanizmu

2. 1 Metoda grafoanalityczna (metoda planów)

Plany prędkości i przyspieszeń rysuję w podziałce k_V =

dla prędkości i k_a =

dla przyspieszeń.

PLAN PRĘDKOŚCI:

Ponieważ człon 2 porusza się ruchem płaskim, a jego ruch jest złożeniem ruchu obrotowego członu 1 (ruch unoszenia) i ruchu postępowego wzdłuż członu 1:

ω₂ = ω₁

V_A = 0

Z planu prędkości odczytuję wartości:

V_B2 = 3,2878
V_CB = 0,6

V_C2 = V_D = 3,8637
V_B2B1 = 3,1321

V_S2 = 3,5794

PLAN PRZYSPIESZEŃ:

Ponieważ ω₁ jest stała:

ε₁ = ε₂ = 0

=
= 2

=
= 12,5284

=
= 1,2

=
= 0,6

Z planu przyspieszeń odczytuję:

a_B2 = 52,7446
a_S2 = 52,8904

a_C2 = a_D = 53,0425

2. 2 Metoda analityczna

Kąt φ₁(t) definiuje ruch mechanizmu w czasie.

φ₂ = φ₁ -

l₁(t) i l₃(t) są funkcjami zmiennymi w czasie.

Wartości stałe i niezależne od czasu:

l₂ = 0,3 m

l₀ = 0,4156 m

φ₃ =

Dla zadanego położenia:

Mechanizm zapisuję wielobokiem wektorowym:

Po zrzutowaniu równania na osie układu współrzędnych mam:

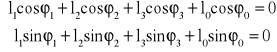
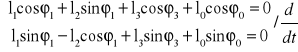
Po zróżniczkowaniu obu równań:

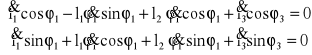
Obliczam wartości prędkości V_B2B1 i V_C2

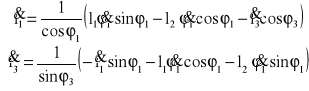
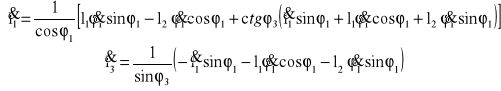
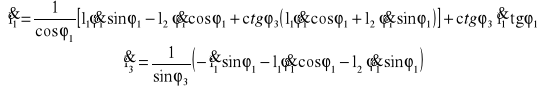
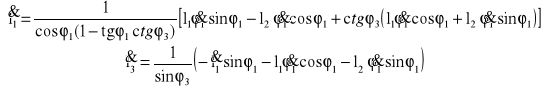
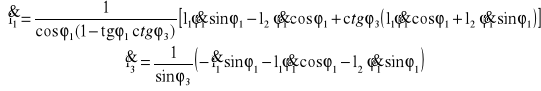
Po podstawieniu wartości dla zadanego położenia:

V_B2B1 = 3,1321

V_C2 = 3,8637

Po zróżniczkowaniu równań prędkości obliczam wartości przyspieszeń

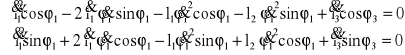
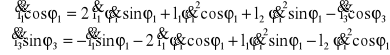
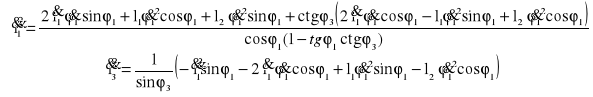
Po podstawieniu wartości dla zadanego położenia:

a_C2 = 53,0418

2. 3 Analiza kinematyczna mechanizmu za pomocą programu SAM 6.1

Schemat mechanizmu:

Wykresy:

2. 4 Zestawienie wyników dla zadanego położenia w tabeli:

	Metoda planów	Metoda analityczna	SAM
VB2	3,2878		3,294
VS2	3,5794		3,581
VC2 = VD	3,8637	3,8637	3,871
VB2B1	3,1321	3,1321
aB2	52,7446		52,945
aS2	52,8904		53,092
aC2 = aD	53,0425	53,0418	53,246
	53,2351	53,2344

3. Analiza kinetostatyczna mechanizmu

Przyjmuję:

P₃ = 200 N

M₂ = 120 Nm

m₂ = 10 kg

Wyznaczam siły bezwładności i ciężkości, oraz moment od sił bezwładności:

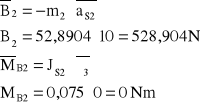
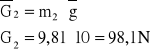
Odrzucenie członu napędzającego i oswobodzenie od więzów.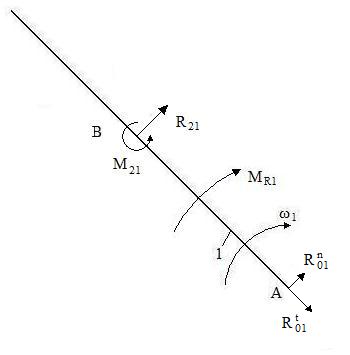

Równania wektorowe równowagi sił działających na grupę strukturalną:

Równanie dla członu 2:

Równanie dla członu 3:

Po zsumowaniu obu równań otrzymuję równanie dla grupy strukturalnej

Reakcje wewnętrzne w grupie znoszą się

Plan sił rysuję w podziałce k_R =

Z planu sił odczytuję

R₁₂ =1442,7921N R₀₃ =1476,5886N

R₃₂ = R₂₃ =

Wyznaczenie uogólnionej siły równoważącej, oraz sił reakcji działających na człon napędzający.

R₀₁ =1442,7921N

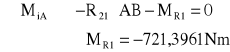
Znak „-” oznacza przeciwny zwrot momentu równoważącego.

Sprawdzenie obliczenia uogólnionej siły równoważącej metodą mocy chwilowych

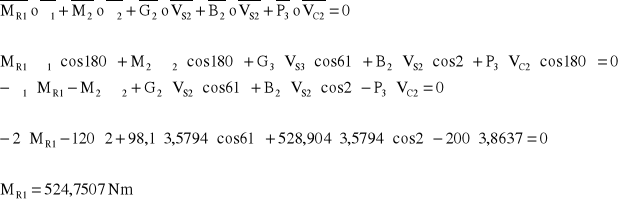
12

---