1. Wektorowy opis ruchu - przemieszczenie, prędkość
2. Wektorowy opis ruchu - przyspieszenie
3. Siła tarcia
- jest zawsze przeciwnie skierowana do kierunku ruchu jednego ciała względem drugiego
- nie zależy od wielkości trących się powierzchni
- doświadczalnie stwierdzono, że jest proporcjonalna do siły nacisku N
FT = μF < to nie jest równanie wektorowe (określa jedynie empiryczną wartość siły tarcia)
- rozróżniamy tarcie statyczne i kinematyczne (dynamiczne)
najczęściej: μs > μk
- tarcie ślizgowe (powyżej) jest o wiele większe od tarcia tocznego
- zjawisko tarcia ma również miejsce w przypadku cieczy i gazów
- aby zmniejszyć tarcie między powierzchnie wprowadza się dodatkową substancję (smar, olej) lub tworzy się łożyska
4. Zasady dynamiki Newtona
I zasada:
Gdy na ciało nie działają żadne siły lub gdy działające siły się równoważą to ciało pozostaje w spoczynku lub porusza się ze stałą prędkością V (ruchem jednostajnym, prostoliniowym). I z.d. jest spełniona w IUO.
II zasada:
Gdy na ciało działa niezrównoważona siła F to ciało porusza się ruchem z przyspieszeniem a proporcjonalnym do działającej siły i odwrotnie proporcjonalnym do masy ciała m.
![]()
Wnioski z I i II z.d.:
- aby podtrzymać ruch nie są potrzebne żadne siły
- siły są konieczne dopiero, gdy chcemy zmienić stan ruchu ciała
III zasada:
Gdy ciało A działa na ciało B z siłą (akcji) FAB to ciało B działa na ciało A z siłą (reakcji) FBA o takiej samej wartości lecz zwróconą przeciwnie.
![]()
(siły te działają wzdłuż prostej, łączącej oba ciała)
Zasady mechaniki (dynamiki) można stosować:
- posługując się IUO i rozważać siły rzeczywiste
lub
- posługując się NIUO ale dodając do sił rzeczywistych siły bezwładności (fikcyjne, pozorne)
5. Inercjalne i nieinercjalne układy odniesienia
IUO mają prędkość stałą (też zerową) V = const. (wektorowo)
NIUO mają prędkość zmienną V ≠ const. (wektorowo)
6. Przykłady ruchu ciał pod działaniem siły grawitacji
- rzut ukośny ( przy powierzchni Ziemi)
- ruch po okręgu ( pod działaniem siły centralnej)
7. Środek masy
- dla układu punktów materialnych:
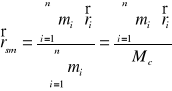
r - współrzędne punktów (wektory)
m - masy punktów
- dla ciała o budowie ciągłej (suma ściśle upakowanych cząstek dm)
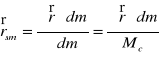
Uwagi:
- położenie środka masy jest niezależne od przyjętego układu współrzędnych. Zależy tylko i wyłącznie od mas punktów i ich wzajemnego rozmieszczenia.
Na przykład przyjmując początek układu współrzędnych w środku masy (czyli r = 0) otrzymamy 0.
- jednorodne układy o elementach symetrii mają środek masy położony na tych elementach symetrii (np. w punkcie (kula), na osi (walec))
![]()
Iloczyn całkowitej masy układu punktów materialnych i przyspieszenia jego środka masy równa się sumie wektorowej Fc wszystkich sił działających na układ. Środek masy układu punktów porusza się w taki sposób, jakby cała masa układu była skupiona w środku masy i jakby wszystkie siły zewnętrzne nań działały (suma Fc tych sił jest przyłożona do środka masy)
Uwagi:
- podane równania obowiązują dla każdego układu punktów materialnych. Układ może być ciałem sztywnym, w którym punkty mają stałe położenie względem siebie. Może być również zbiorem cząstek, w których występują wszystkie rodzaje ruchu wewnętrznego (drgania, obrót, …). Środek masy każdego układu niezależnie od tego, jaki jest ten układ, oraz niezależnie od ruchu jego poszczególnych części, porusza się zgodnie z podanymi wcześniej równaniami.
- ruch środka masy ciała (ruch postępowy ciała) możemy otrzymać zakładając, że cała masa tego ciała jest skupiona w środku masy i wszystkie siły zewnętrzne działają na ten punkt.
- gdy siłą zewnętrzną jest siła ciężkości, wtedy działa ona na środek ciężkości ciała. W większości przypadków środek ciężkości pokrywa się ze środkiem masy, który jest pojęciem bardziej ogólnym.
8. Pęd dla pojedynczego ciała i układu ciał. Zasada zachowania pędu
![]()
(wektor)
Uwaga:
Ponieważ pęd ciała jest proporcjonalny do prędkości, zależy więc od układu odniesienia obserwatora. Układ ten musimy zawsze ustalić zanim określimy pęd.
Z wcześniejszego równania dla ruchu środka masy układu:
![]()
stąd:
![]()
Całkowity pęd układu punktów materialnym jest równy sumie (wektorowej) pędów poszczególnych punktów.
Całkowity pęd układu punktów materialnych jest równy też iloczynowi całkowitej masy układu i prędkości jego środka masy. (w tym samym układzie odniesienia)
Z wcześniejszego równania dla ruchu środka masy układu:
![]()
Ale można napisać (przy założeniu, ze Mc = const.):
![]()
![]()
zatem:
![]()
Zmiana całkowitego pędu układu ciał w jednostce czasu (pochodna całkowitego pędu po czasie) jest równa całkowitej (wypadkowej) sile działającej na ten układ ciał (wektorowo).
Zasada zachowania pędu:
Jeżeli całkowita suma wszystkich sił zewnętrznych działających na układ jest równa zeru:
![]()
to całkowity wektor pędu tego układu pozostaje stały
![]()
Zasada zachowania pędu jest bardziej fundamentalna niż zasady Newtona (obowiązuje również w mechanice kwantowej)
Uwagi:
- zasada zachowania pędu ( przy zerowaniu się wypadkowej sił zewnętrznych) obowiązuje dla wszystkich obserwatorów w różnych układach odniesienia ( wyznaczą różne wartości całkowitego pędu układu, lecz każdy z nich zgodzi się, że ustalona przez niego wartość pędu pozostaje nie zmieniona, gdy punkty materialne tworzące układ przemieszczają się.
- całkowity pęd układu może być zamieniony tylko przez siły zewnętrzne działające na ten układ.
- pęd jest wielkością wektorową zasada zachowania pędu jest równoważna trzem równaniom skalarnym dla trzech kierunków przestrzeni napisanym z uwzględnieniem kierunków i zwrotów wszystkich pędów w układzie.
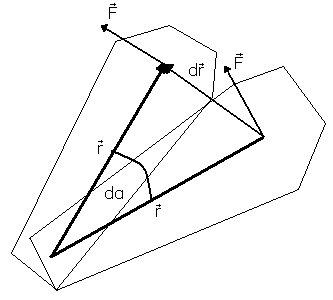
9. Praca w ruchu postępowym
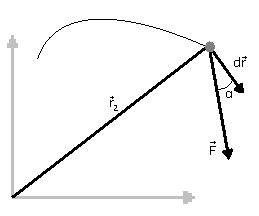
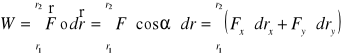
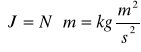
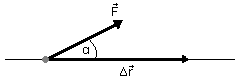
Pracę W (gdy siła i przemieszczenie są wektorami stałymi) wyrażamy skalarnym iloczynem siły i przemieszczenia ciała:
![]()
Uwaga:
Praca powstaje ze skalarnego iloczynu dwóch wielkości wektorowych. Jest więc skalarem.
![]()
Praca to iloczyn wartości składowej siły w kierunku przemieszczenia ciała przez wartość przemieszczenia ciała ( lub iloczyn wartości składowej przemieszczenia ciała w kierunku działania siły przez wartość tej siły)
Uwaga:
- jeżeli na ciało działa kilka sił to całkowita praca jest sumą prac wykonanych przez poszczególne siły
(alternatywnie można zsumować siły wektorowo i obliczać pracę siły wypadkowej Ww)
![]()
- praca wykonana przez siłę wypadkową przy przemieszczeniu punktu materialnego jest równa pracy, jaką wykonuje ten punkt przeciwko tej sile wziętej ze znakiem minus (konsekwencja III zasady dynamiki)
Wnioski:
- praca (mimo fizycznego wysiłku) może być zerowa
- praca może być dodatnia: cosα > 0
- praca może być ujemna: cosα < 0
Praca wykonana przez wypadkową siłę może przyczynić się do zmiany energii kinetycznej ciała (twierdzenie o pracy i energii)
10. Moc w ruchu postępowym
Moc (skalar) jest miarą szybkości wykonywania pracy.
- Moc średnia (całkowita praca podzielona przez całkowity czas)
![]()
- Moc chwilowa:
![]()
![]()
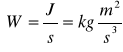
Uwaga:
- Ponieważ: ![]()
Na przykład w ruchu jednostajnym moc jest równa iloczynowi siły oraz prędkości (średnią)
11. Energia kinetyczna
Energia kinetyczna ciała: ![]()
Energia ( jakakolwiek) i praca mają te same jednostki. Energia (jak i praca) jest skalarem.
Uwagi:
- energia kinetyczna jest związana z ruchem ciała i jest równa pracy jaką może wykonać to ciało, zanim się zatrzyma.
- jeżeli wartość prędkości jest stała to nie ma zmiany energii kinetycznej i praca siły wypadkowej jest równa zeru
- również w ruchu jednostajnym po okręgu W=0 ( bo pracę nad punktem materialnym wykonuje jedynie składowa siły mająca kierunek zgodny z kierunkiem tego ruchu)
- jeżeli energia kinetyczna punktu materialnego maleje, to o wielkość równą dokładnie pracy jaką wykonuje ten punkt.
- jeżeli energia kinetyczna punktu materialnego maleje, praca wykonana przez siłę wypadkową przy przemieszczeniu tego punktu jest ujemna ( przemieszczenie i składowa siły wypadkowej w kierunku ruchu są skierowane przeciwnie)
- energia kinetyczna zespołu punktów materialnych jest po prostu sumą energii kinetycznych poszczególnych punktów (sumą algebraiczną bo energia jest skalarem)
- energia kinetyczna nie może być ujemna ( w fizyce nie występuje pojęcie prędkości urojonej)
- bezwzględna wartość energii kinetycznej zależy od wyboru układu odniesienia jednak często interesujące są bardziej zmiany tej energii niż jej wartość absolutna
12. Energia potencjalna
Uwagi:
- nie można podać ogólnej formuły opisującej energie potencjalną (w przeciwieństwie do energii kinetycznej) postać wzorów na energie potencjalną zależy od sytuacji i rodzaju oddziaływań (grawitacyjne, elektrostatyczne, sprężystości)
- energia potencjalna jest związana z położeniem układu ciał i jest równa pracy którą ten układ może wykonać zmieniając względne położenie swoich części, czyli zmieniając swój stan
- w każdym przypadku musimy określić, jaką pracę może wykonać układ przechodząc z jednego stanu do innego i potraktować tą pracę, jako różnicę energii potencjalnych układu między tymi dwoma stanami
- pojecie energii potencjalnej ma sens tylko w odniesieniu do sił zachowawczych
- energia potencjalna może być zarówno potencjalna jak i ujemna (w przeciwieństwie do energii kinetycznej)
Wnioski:
- Fizyka nie wskazuje żadnego konkretnego punktu (poziomu) odniesienia z jednoznaczną wartością energii potencjalnej
- zatem sami musimy obrać dowolny punkt (poziom) odniesienia i przypisać mu dowolna wartość energii potencjalnej (najczęściej zero) a następnie konsekwentnie trzymać się tego przyporządkowania
- powyższe przyporządkowania zwykle ustalamy tak, alby wygodne były dalsze rachunki (np. Punkt odniesienia w miejscu początku lub końca ruchu w nieskończoności lub w miejscu gdzie siła zachowawcza jest równa zeu)
- przy obliczeniach interesują nas zawsze tylko różnice energii potencjalnej, a nie jakaś absolutna wartość tej energii w danym punkcie
- praca wykonana nad ciałem przez siłę zachowawczą jest równa przyrostowi jego energii potencjalnej, wziętemu ze znakiem minus
- dowolność obrania poziomu odniesienia dla energii potencjalnej jest podobna do dowolności obrania układu odniesienia dla energii kinetycznej. W obu przypadkach interesują nas bardziej zmiany tych energii niż ich bezwzględne wartości
- Jednak dla jednoznaczności obliczeń zawsze należy obrać konkretny układ odniesienia (dla energii kinetycznej) lub poziom odniesienia (dla energii potencjalnej)
-energia potencjalna to funkcja położenia której ujemna pochodna (przestrzenna) daje wyrażenie na działającą siłę (zachowawczą)
13. Zasada zachowania energii w obecności działania sił (zachowawczych i niezachowawczych)
Zasada zachowania energii mechanicznej:
Jeżeli w układzie działają tylko siły zachowawcze wówczas całkowita energia mechaniczna układu pozostaje stała:
![]()
Całkowita energia mechaniczna Ecm jest wówczas stałą ruchu.
Uwagi:
- zasada zachowania energii mechanicznej obowiązuje w wybranym zamkniętym układzie obiektów, które mogą oddziaływać na siebie wyłącznie siłami zachowawczymi
- przykładem może być układ rzucone ciało - ziemia (tuż po rzucie i tuż przed chwytem rzucającego)
- energia potencjalna zmagazynowana jest w układzie rzucone ciało - ziemia
- teoretycznie prócz rzuconego ciała również Ziemia się porusza (zasada zachowania pędu) jednak jej ruch jest tak znikomy, że go pomijamy i bierzemy pod uwagę tylko ruch rzuconego ciała
- przyjmujemy zatem, że energia kinetyczna zmagazynowana jest w poruszającym się ciele
- jak widać, w ogólności energia potencjalna i kinetyczna mogą występować w różnych częściach układu i stosunki między nimi mogą być zmienne gdy stan układu ulega zmianom.
Z zasady zachowania energii mechanicznej można mieć pełen pożytek, gdy potrafimy obliczać energię potencjalną
Siła jest zachowawcza, jeżeli praca wykonana przez tę siłę nad punktem materialnym, który porusza się po dowolnej drodze zamkniętej jest równa zeru.
W poziomie siła grawitacji (pionowa) nie wykonuje pracy (poziome składowe przemieszczenia są nieistotne)
Dla wykonanej pracy istotne są tylko pionowe składowe przemieszczenia
Siły niezachowawcze:
- jeżeli punkt materialny po przebyciu drogi zamkniętej, wraca do punktu wyjścia ze zmienioną energią kinetyczną (większą lub mniejszą) oznacza to, iż przynajmniej jedna z działających w układzie sił jest niezachowawcza
- siła jest niezachowawcza, jeżeli praca wykonana przez tę siłę nad punktem materialnym, który porusza się po dowolnej drodze zamkniętej, nie jest równa zeru
- siłę nazywamy niezachowaczą jeżeli praca wykonana przez tę siłę nad punktem materialnym poruszającym się pomiędzy dwoma punktami zależy od kształtu drogi łączącej te punkty
Najpopularniejszą siłą niezachowawczą jest siła tarcia. Jest przykładem siły rozpraszającej (dysupatywnej), która wykonuje nad ciałem pracę ujemną i dąży do zmniejszenia całkowitej energii mechanicznej układu. Siła tarcia powoduje jednocześnie zmianę energii wewnętrznej ciał ΔUwew co przejawia się wzrostem ich temperatury
Istnieją również inne siły niezachowawcze, powodujące zmiany energii mechanicznej układu przy jednoczesnych zmianach innych form energii
Zasada zachowania energii całkowitej
Energia całkowita układu Ec nie zmienia się. Energia może być przekształcona z jednej formy w inna, ale nie może być wytwarzana, ani niszczona energia całkowita jest wartością stałą.
Uwagi:
- energia mechaniczna (kinetyczna i potencjalna) jest zachowana tylko w przypadku działania sił zachowawczych
- energia całkowita jest zachowana zawsze (niezależnie od rodzaju działających sił)
14. Parametry ruchu obrotowego a parametry ruchu postępowego
Dla wygody wprowadza się do opisu ruchu obrotowego dodatkowe parametry ułatwiające rachunki (przemieszczenie, prędkość i przyspieszenie kątowe) W rozważaniach jakie nastąpią zakładamy, że początki wektorów wodzących (punktu odniesienia) i osie obrotu są nieruchome względem IUO
Ciało (sztywne) wykonuje ruch obrotowy, jeżeli każdy punkt tego ciała porusza się po okręgu a środki wszystkich okręgów leżą na linii prostej zwaną osia obrotu.
Jeżeli poprowadzimy linię prostopadłą do osi obrotu z jakiegokolwiek punktu ciała sztywnego to każda taka linia będzie zakreślała ten sam kąt w tym samym czasie. Zatem możemy opisać czysty ruch obrotowy ciała sztywnego, opisując ruch dowolnie wybranego punktu tego ciała (z wykluczeniem punktów na osi obrotu)
Parametry ruchu obrotowego ciała:
- przyrost kąta w radianach: ![]()
- średnia prędkość kątowa: ![]()
- chwilowa prędkość kątowa: ![]()
- średnie przyspieszenie kątowe: ![]()
- chwilowe przyspieszenie kątowe: ![]()
Zależność między (wartościami) parametrów ruchu postępowego i obrotowego:
- zależność między s i α można zapisać i zróżniczkować po czasie jako:
![]()
- zależność między V i ω można zapisać i zróżniczkować po czasie jako:
![]()
Można również wektorowo wykazać że
![]()
Odpowiadające sobie parametry:
Ruch postępowy |
Ruch obrotowy |
s |
α |
V |
ω |
a |
ε |
15. Moment siły a moment pędu
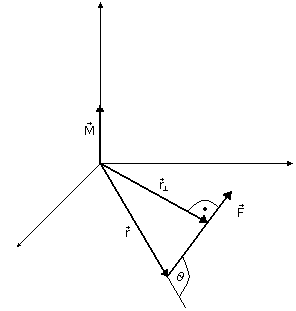
![]()
Moment siły - moment obrotowy (wektor)
![]()
- ramię siły
Uwagi:
- Moment siły jest wynikiem iloczynu wektorowego
- Moment siły w ruchu obrotowym jest odpowiednikiem siły w ruchu postępowym
- Tylko niezerowy moment siły może wpłynąć na ruch obrotowy ciała (sama siła nie wystarczy - musi działać jeszcze na niezerowym ramieniu)
- Moment siły zależy nie tylko od wartości siły i jej kierunku, lecz także od pozycji ramienia siły względem początku układu odniesienia (który należy wcześniej zdefiniować)
- Moment siły ma ten samy wymiar (jednostkę) co praca. Ale są to całkowicie różne wielkości fizyczne
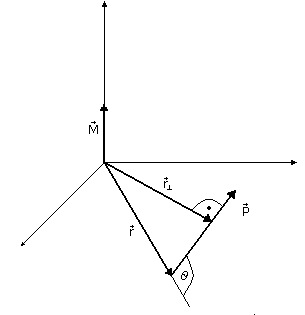
Moment pędu (wektor)
![]()
- ramię pędu
Uwagi:
- Moment pędu jest wynikiem iloczynu wektorowego
- moment pędu w ruchu obrotowym jest odpowiednikiem pędu w ruchu postępowym
- moment pędu zależy nie tylko od wartości pędu i jego kierunku, lecz także od pozycji ramienia pędu względem początku układu odniesienia (który należy wcześniej zdefiniować)
Zależność miedzy momentem siły i momentem pędu:
Równanie ![]()
mnożymy lewostronnie wektorowo przez ![]()
:
![]()
(1)
Równanie ![]()
różniczkujemy po czasie:
![]()
Ale ![]()
ponieważ ![]()
i ![]()
są równoległe
Mamy zatem: ![]()
(2)
Równania 1 i 2 mają identyczne prawe strony zatem można przyrównać ich strony lewe:
![]()
Wnioski:
- zmiana momentu pędu punktu materialnego w jednostce czasu jest równa momentowi siły działającej na ten punkt
- powyższy wniosek jest równoważny stwierdzeniu, ze stosunek zmiany pędu punktu materialnego od czasu, w którym ta zmiana nastąpiła, jest równy sile działającej na ten punkt
- wektorowe równanie zależności miedzy momentem siły i momentem pędu jest równoważne trzem równaniom skalarnym (składowa x(y,z) momentu siły dana jest przez składową x(y,z) czasowej zmiany momentu pędu)
16. Energia kinetyczna w ruchu obrotowym. Moment bezwładności
Praca (moc) momentu siły wykonana nad bryłą sztywną:
![]()
Wiemy, ze:
![]()
Zatem otrzymujemy:
![]()
Dzieląc (różniczkując przez przyrost czasu dr)
![]()
Ale ![]()
Zatem ostatecznie:
![]()
(1)
Z drugiej strony wykonana nad ciałem praca dW będzie powodowała zmianę energii kinetycznej ruchu obrotowego dEk:
dW=dEk
dzieląc (różniczkując) powyższe równanie przez przyrost czasu dt (zakładając, że I=const (bryła sztywna)):
![]()
Ale znowu ![]()
zatem otrzymujemy: ![]()
(2)
Równania 1 i 2 mają identyczne lewe strony zatem można przyrównać ich strony prawe: ![]()
Zatem ostatecznie (po skróceniu ω): ![]()
(3)
Uwagi:
- równanie 3 jest równaniem skalarnym dotyczy zatem momentów sił, prędkości kątowych i przyspieszeń kątowych leżących wzdłuż wspólnej osi (zgodne kierunki) i przyjmujących zgodne zwroty
- równanie 3 jest odpowiednikiem IIz.d. dla ruchu obrotowego (przekształcona do postaci wygodnej w ruchu obrotowym)
- Tak jak siła ma związek z przyspieszeniem ciała w ruchu postępowym, tak moment siły ma związek z przyspieszeniem kątowym ciała dookoła własnej osi. Moment bezwładności I jest miarą oporu ciała, przeciw zmianie jego ruchu obrotowego przez moment siły.
17. Praca i moc w ruchu obrotowym
18. Zasada zachowania momentu pędu. Przykłady jej konsekwencji
![]()
(1)
Jeżeli wypadkowy moment sił zewnętrznych działających na układ wynosi zero:
![]()
To na podstawie równania 1 całkowity wektor momentu pędu tego układu pozostaje stały:
![]()
Zasada zachowania momentu pędu jest zasadą bardziej fundamentalną niż zasady Newtona
Uwagi:
- całkowity moment pędu układu może być zmieniony tylko przez niezerowy wypadkowy moment sił zewnętrznych działających na ten układ.
- przy braku (lub zerowaniu się) momentów siły zewnętrznych całkowity wektor momentu pędu układu pozostaje stały (ale wektory momentów pędu poszczególnych punktów materialnych mogą się zmieniać, lecz ich suma wektorowa pozostaje stała)
- moment pędu jest wielkością wektorową. Zasada zachowania pędu jest równoważna trzem równaniom skalarnym dla trzech osi współrzędnych przechodzących przez punkt odniesienia. Na podstawie zasady zachowania momentu pędu otrzymujemy trzy warunki na ruch układu.
19. Siła i energia potencjalna sprężystości
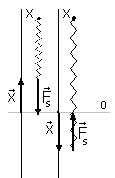
Siła sprężystości:
![]()
(1)
też skalarnie:
![]()
(2)
k - współczynnik sprężystości sprężyny (skalar)
Uwagi:
- równania 1 i 2 są zależnościami empirycznymi. Jest to specjalny przypadek ogólnej zależności dotyczącej deformacji ciał sprężystych zwanej prawem Hooke'a. Stwierdza ono, że odkształcenie ciała jest proporcjonalne do przyłożonego naprężenia. Prawo to dotyczy wielu rodzajów ciał pod warunkiem, że deformacja nie jest duża (nie przekracza graniczy sprężystości - ciało ma możliwość powrotu do pierwotnego kształtu i rozmiarów)
- siła sprężystości jest siłą przywracającą równowagę układu
- siła sprężystości ( w granicach stosowania prawa hooke'a) jest siłą zachowawczą
Energia potencjalna sprężyny
Wzór na Ep siły zachowawczej:
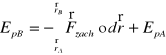
W przypadku sprężyny (zakładając EpA=0 dla x=0)
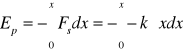
Stąd:
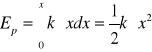
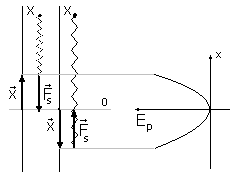
Ep sprężyny: ![]()
< Zależność paraboliczna
Uwagi:
- Do końca sprężyny o współczynniku sprężystości k mocujemy ciało o masie m. Samą sprężynę uznajemy jako pozbawioną masy
- dla prostoty rachunków pomijamy ciężary ciał (brak pola grawitacyjnego)
20. Równanie ruchu harmonicznego prostego i jego rozwiązanie
21. Energia w ruchu harmonicznym prostym
22. Wahadło fizyczne, wahadło matematyczne
Wahadło fizyczne
To dowolne ciało sztywne o masie m zawieszone (w polu grawitacyjnym) tak, że może się wahać dookoła pewnej osi (względem której ma moment bezwładności I)
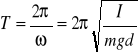
![]()
Wahadło matematyczna
To punktowa masa m zawieszona na nieważkiej nierozciągliwej nici o długości l. jest to szczególny przypadek wahadła fizycznego.
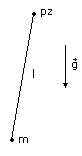
![]()
Okres i f ruchu wahadła matematycznego:
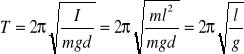
![]()
23. Ruch harmoniczny tłumiony
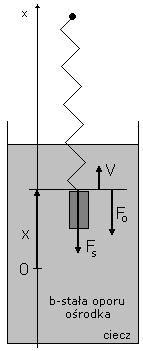
Ciężarek m na sprężynie k w cieczy b
Ruch harmoniczny tłumiony:
Siła oporu ośrodka:
![]()
Podobnie jak siła sprężystości:
![]()
W równaniu:
![]()
Zatem otrzymujemy analogiczne równanie z dodatkowym składnikiem:
![]()
Wnioski:
- w przedstawionym modelu siła tarcia jest proporcjonalna do prędkości (najczęstszy przypadek)
- częstość ω` (przy tłumieniu) jest mniejsza od normalnej. ω (bez tłumienia)
- w ruchu harmonicznym tłumionym energia oscylatora w wyniku tarcia ulega stopniowemu rozpraszaniu i z biegiem czasu zmniejsza się do zera
- czas po którym amplituda ruchu drgającego spada do 1/e wartości początkowej nazywamy średnim czasem życia oscylacji
- uzyskane rozwiązanie obowiązuje dla małej stałej oporu b. Gdy siła tarcia jest dostatecznie duża to b również rośnie i rozwiązanie przestaje być ruch okresowy. Wówczas ciało bez oscylacji powraca do położenia równowagi
24. Ruch harmoniczny wymuszony. Rezonans
Uwagi:
- drgania wymuszone mają częstość taką z jaką działa siła zewnętrzna ω'' nie taka jaka jest częstość własna
ciała ω
- reakcja ciała (amplitud ruchu) zależy od stosunku jaki zachodzi pomiędzy częstością wymuszoną ω'' a częstością własną ω
- dla pewnej charakterystycznej wartości częstości wymuszającej ω'', amplituda oscylacji osiąga maksimum. Takie zjawisko nazywa się rezonansem
- częstość ω'' przy której pojawia się maksymalna amplituda drgań wymuszonych danego układu nazywamy częstotliwością rezonansową. Im mniejsze tłumienie b tym częstość rezonansowa ω'' bliższa jest częstości ω układu nie tłumionego
- kolejne impulsy siły wymuszającej nawet niewielkie, ale następujące w odpowiednich chwilach (zsynchronizowane) mogą doprowadzić do drgań o dużej amplitudzie
25. Zależność między ruchem harmonicznym prostym a ruchem po okręgu
Wnioski:
- ruch harmoniczny prosty można opisać jako rzut jednostajnego ruchu po okręgu na jego średnicę
- prędkość kątowa ω modelowanego punktu poruszającego się po okręgu jest równa częstości ω w ruchu harmonicznym prostym
- odpowiednie składowe ruchu po okręgu są identyczne do ruchu harmonicznego prostego
- faza początkowa (stała fazowa) φ ruchu po okręgu będzie odpowiadała początkowej sytuacji ruchu harmonicznego
- metoda wirujących wykresów (wskazowych) jest powszechnie stosowana w opisie zjawisk periodycznych. Znacząco ułatwia ukazanie zależności fazowych między przebiegami.
26. Opis propagacji pojedynczego zaburzenia oraz fali sinusoidalnej w ośrodku sprężystym
27. Interferencja fal o tych samych częstotliwościach
Uwagi:
- w sytuacji nakładania się fal o tych samych częstotliwościach możemy wyróżnić dwie skrajne sytuacje
- wzmocnienia
Gdy różnice faz Δφ lub dróg Δr spotykających się fal wynoszą:
Δφ = π, 3π, 5π, …, (2n+1)π
![]()
Gdzie n = 0,±1,±2,… jest rzędem wzmocnień lub osłabień (wygaszeń)
O tym gdzie występują wzmocnienia i osłabienia decyduje geometria sytuacji (interferencja w przestrzeni)
28. Interferencja fal różniących się częstotliwościami
Wnioski:
- Z wielu fal składowych można zbudować skomplikowaną falę złożoną
- istnieje też możliwość operacji odwrotnej: rozłożenia skomplikowanych ruchów falowych na kombinację fal prostych (analiza Fouriera)
Dowolny (skomplikowany) periodyczny rucha falowy (cząsteczek) może być przedstawiony w postaci kombinacji liniowej (sumy) ruchów harmonicznych prostych (sinusoidalnych)
- Gdy ruch nie jest periodyczny (pojedynczy impuls) suma zostaje zastąpiona tzw. Całka Fouriera (kombinacja nieskończenie wielu ruchów harmonicznych prostych) zatem zjawiska impulsowe będą produkowały szerokie spektrum sygnałów sinusoidalnych (zakłóceń np. elektrycznych)
- powyższe wnioski wynikają z zasady superpozycji
- z powyższych powodów bardzo istotne jest zagadnienie ruchu (falowego) harmonicznego prostego
Uwagi:
- prędkość fal w ogólności może zależeć od ich częstotliwości. Mówimy wówczas o dyspersji
- w ośrodku dyspersyjnym fale (impulsy) złożone z elementarnych fal prostych będą w trakcie propagacji zmieniały swój kształt (fale składowe rozjeżdżają się w czasie i przestrzeni)
- zmiana kształtu fal i impulsów może zachodzić również w wyniku pochłaniania energii przez ośrodek (dyssypacja energii - fale gasnące)
29. Efekt Dopplera dla fal mechanicznych
Nieruchome źródło emituje falę o częstotliwości f długości fali![]()
i prędkością ![]()
Gdy obserwator (słuchacz) porusza się z prędkością ![]()
w kierunku „do” źródła (+) lub od źródła (-) wówczas będzie obserwował kolejne długości fal docierające do niego z (słyszalną) częstotliwością
(1)
Ruchomy obserwator będzie „odbierał” sygnał o częstotliwości większej (+) lub mniejszej (-) od „nadawanej” przez nieruchome źródło
Źródło poruszające się z prędkością Vz w kierunku do obserwatora (-) lub od obserwatora (+) emituje falę o częstotliwości f i okresie T (względem źródła) oraz prędkości V i długości ![]()
. W wyniku ruchu źródła długość ta jest krótsza (-) lub dłuższa (+) w stosunku do ![]()
o składnik Vz T:
![]()
(2)
Nieruchomy obserwator (słuchacz) będzie odbierał kolejne długości fal (np grzbiety) docierające do niego z (słyszalną) częstotliwością
![]()
Uwaga:
-W najbardziej ogólnej sytuacji gdy zarówno obserwator jak i źródło poruszają się z prędkościami odpowiednio ![]()
oraz ![]()
, wzór na odbieraną (słyszalną) przez obserwatora częstotliwość ![]()
ma postać:
![]()
Gdzie:
- Znaki górne (+ w liczniku i - w mianowniku) odpowiadają sytuacji gdy obserwator i źródło poruszają się wzdłuż łączącej je prostek w kierunku do siebie (odbierana (słyszana) przez obserwatora częstotliwość fo jest większa niż częstotliwość emitowana przez źródło
- Znaki górne (- w liczniku i + w mianowniku) odpowiadają sytuacji gdy obserwator i źródło poruszają się wzdłuż łączącej je prostek w kierunku „od” siebie (odbierana (słyszana) przez obserwatora częstotliwość fo jest mniejsza niż częstotliwość f emitowana przez źródło
Uwagi:
-w przypadku fal mechanicznych o prędkości fali V decyduje ośrodek, w którym się ona propaguje i wszystkie inne (![]()
,![]()
) są mierzone względem tego ośrodka
-w przypadku fal elektromagnetycznych efekt Dopplera również występuje. Jednak nie potrzebują one ośrodka materialnego, który by je przenosił i ich prędkości względem źródła, a także względem obserwatora ma zawsze tę samą wartość niezależnie od ruchu tych ciał względem siebie. Dlatego wzór Dopplera dla fal elektromagnetycznych ma inną postać niż dla fal mechanicznych (choć zjawiska są jakościowo podobne)
-efekt Dopplera ma ogromne znaczenie i wiele zastosowań w takich dziedzinach jak transmisja sygnałów i łączności ,metrologia, medycyna, astronomia, spektroskopia itd.
30. Temperatura i jej interpretacja. „Zerowa” zasada termodynamiki
-analizując zjawisko fizyczne (termodynamiczne) możemy mówić o:
Układzie (myślowo wyodrębnionym z otaczającego świata),
Otoczenia ( wszystkie poza układem co ma wpływ na jego zachowanie)
Przykłady:
-rzucony kamień (układ), powietrze i Ziemia (otoczenie)
-gaz w zbiorniku (układ), podgrzewane palnikiem ścianki zbiornika (otoczenie)
-kawałki lodu (układ) pływające w wodzie (otoczenie)
-ale też : mieszanina wody z lodem (układ), szklanka i powietrze (otoczenie)
Zwykle tak dobieramy układ i otoczenie, aby można było wygodnie określić zachowanie układu i analizować jego oddziaływanie z otoczeniem
Uwagi:
Opisując zachowanie układu posługujemy się wielkościami:
-makroskopowymi (cechy układu jako całości), np temperatura T, ciśnienie P, objętość V, energia wewnętrzna U, entropia S itp., Wielkości te często są bezpośrednio związane z naszymi doznaniami zmysłowymi
Lub
-mikroskopowymi (cechy składników tworzących układ - atomów, cząsteczek…), np: prędkości, energia, masy, momenty pędu, zachowanie podczas zderzeń itp. Wielkości te nie są bezpośrednio związane z naszymi doznaniami zmysłowymi
Termodynamika zajmuje się opisem zjawisk cieplnych posługując się wielkościami makroskopowymi
Mechanika statystyczna posługuje się wielkościami mikroskopowymi
Dla dowolnego układu wielkości makroskopowe i mikroskopowe muszą być ze sobą związane: są one po prostu innymi sposobami opisu tej samej rzeczywistości
np ciśnienie gazu (wielkość makroskopowa) jest miarą średniej szybkości przekazu pędu cząsteczek gazy do jednostkowej powierzchni ścianki naczynia (wielkość mikroskopowa)
temperatura:
Łączymy dwa ciała : A(gorące) z B(zimne)
Po odpowiednio długim czasie ich temperatury będą identyczne
Mówimy ,że takie ciała są w równowadze termicznej
Wprowadzamy ciało C (termometr) który osiąga równowagę termiczną zarówno z ciałem A, oraz z ciałem B i wskazuje temperaturę (wspólną dla wszystkich trzech ciał A, B, C)
Zerowa zasada termodynamiki:
Jeżeli każde z dwóch ciał A i B jest w równowadze termicznej z trzecim ciałem C(termometrem) to A i B są w równowadze termicznej ze sobą
Lub w innym sformułowaniu:
Istnieje wielkości skalarna, nazywana Temperaturą, która jest właściwością wszystkich układów termodynamicznych (w stanach równowagi), taka że równość temperatur jest warunkiem koniecznym i wystarczającym równowagi termicznej
Uwagi:
- myśl zawarta w zerowej zasadzie termodynamiki, choć prosta, nie jest wcale oczywista. Na przykład osoby A i B mogą znać osobę C ale nie muszą znać się wzajemnie
- istotą zerowej zasady termodynamiki jest stwierdzenie ze istnieje bardzo użyteczna wielkość zwana temperaturą.
31. Pomiary temperatury
Pomiar temperatury można zrealizować przy pomocy ciała termometrycznego przejawiającego określoną cechę termometryczną (zależną od temperatury)
np ciała termometryczne (cecha termometryczna) : pręt metalowy (długość pręta), spirala bimetaliczna (skręcanie kątowe spirali), włókno żarówki (kolor - widmo emitowanego światła), przewodniki lub półprzewodniki (opór elektryczny) ciecz w rurce (długość słupa cieczy ), gaz w naczyniu (ciśnienie gazu).
Palec jako termometr
- Palec może być dobrym czujnikiem temperatury
- Jeżeli wytrzymamy 5 sekund z palcem przytkniętym do gorącego elementu, to wielkość radiatora jest mniej więcej właściwa, a temperatura obudowy wynosi około 85![]()
C
- Jeżeli element jest zbyt gorący by go dotknąć dłużej to mokrym palcem (woda, ślina) dotkniemy na ułamek sekundy elementu: jeśli ślad tylko szybko wysycha to obudowa ma nie więcej niż 100![]()
C.
- Jeżeli zacznie skwierczeć to ma powyżej 100![]()
C
Pomiary temperatury:
- W ogólności określony wybór ciała termometrycznego i cechy termometrycznej - wraz z założeniem określającym (liniowy) związek tej cechy z temperaturą - prowadzi do jakiejś szczególnej skali temperatury. Pomiary wykonywane przy użyciu tej skali niekoniecznie będą się zgadzać z pomiarami wykonywanymi przy zastosowaniu dowolnej innej niezależnie zdefiniowanej skali temperatury
- Aby otrzymać jednoznacznie określoną skalę temperatury, należy wybrać jeden ,określony rodzaj termometru jako wzorcowy, oraz określić (arbitralnie) jego temperaturę w punkcie wzorcowym (standardowym),
-Jako wzorcowy (precyzyjny i użyteczny do formułowania praw fizyki) wybrano termometr gazowy o stałej objętości. Przyjęto, że w punkcie potrójnym wody (gdy para wodna ,woda i lód współistnieją w równowadze termicznej) przy ciśnieniu 4,58mm Hg wskazuje on temperaturę 273,16 [K - kelwin].
Bezwzględna termodynamiczna skala temperatur (skala Kelvina)
- Najniższa temperatura jaką można zmierzyć jakimkolwiek termometrem gazowym, jest równa około 1k (temperatura skraplania helu pod niskim ciśnieniem - gazu, który przechodzi w stan ciekły w temperaturze niższej niż jakikolwiek gaz)
- Natomiast przy pomocy przemian termodynamicznych można określić skalę temperatury w sposób niezależny od właściwości jakiejkolwiek określonej substancji. W ten sposób stworzono bezwzględną termodynamiczną skalę temperatury (skalę Kelvina), która ma zero bezwzględne 0K
- Jak dotąd doświadczalnie jedynie zbliżono się do zera bezwzględnego ale nie osiągnięto go
- stan zera bezwzględnego jest stanem odpowiadającym minimalnej (ale nie zerowej) energii ruchu (efekty kwantowe)
- nie istnieją temperatury niższe od 0K
- idealna skala gazowa i skala Kelvina są identyczne w zakresie temperatur, w którym może być użyty termometr gazowy (powyżej około 1K)
Wyznaczanie za każdym razem temperatur przy pomocy gazu doskonałego byłoby pracochłonne i nie praktyczne. Dlatego zdefiniowano Międzynarodową Praktyczną Skalę temperatur (IPTS). Jest to zespół przepisów, które wraz ze stałymi punktami wzorcowymi określają sposób skalowania i kalibrowania przyrządów przemysłowych i naukowych zgodnie ze skalą Kelvina
Stosowane powszechnie skale temperatury
-Skala Celsjusza używa jako jednostki C o tej samej wielkości co „stopień” w stali Kelvina
![]()
-Skala Fahrenheita (nie używana w pracach naukowych)
![]()
Uwagi:
Podczas pomiarów temperatury (pomijając metody bezstykowe - zdalne) należy uwzględniać takie czynniki jak:
-odpowiedni kontakt termiczny badanego układu i czujnika temperatury (termometru)
-czas ustalania równowagi termodynamicznej układu i czujnika
-masy i rozmiary czujnika oraz układu (pojemności cieplne)
-położenie czujnika względem układu i otoczenia
32. Rozszerzalność cieplna
Liniowa:
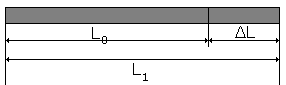
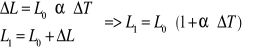
![]()
- przyrost temperatury
![]()
- współczynnik rozszerzalności liniowej Δ
Niektóre wartości ![]()
Dla zakresu temperatury 0 ![]()
100![]()
C (dla lodu -10![]()
0![]()
C)
SUBSTANCJA |
|
Twarda guma |
80 |
Lód |
51 |
Ołów |
29 |
Glin |
23 |
Mosiądz |
19 |
Miedź |
17 |
Stal |
11 |
Szkło (zwyczajne) |
9 |
Szkło (pyrek_ |
3,2 |
Inwar |
0,7 |
Powierzchniowa (dla ciał izotropowych):

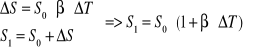
![]()
- przyrost temperatury
![]()
- współczynnik rozszerzalności powierzchniowej (![]()
)
Objętościowa:
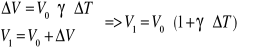
![]()
- przyrost temperatury
![]()
- współczynnik rozszerzalności objętościowej (![]()
)
Uwagi
- w ogólności współczynnika rozszerzalności (![]()
)zależą również od temperatury (lecz dla celów technicznych można je przyjąć jako stałe)
- niektóre ciała w pewnych zakresach temperatury mają ujemne współczynniki rozszerzalności cieplnej (n.p niektóre substancje podobne do gumy, woda w zakresie 0 + 4![]()
C )
- istnieją ciała wykazujące anizotropię rozszerzalności cieplnej (różne współczynniki rozszerzalności w różnych kierunkach - ciała krystaliczne)
- dla cieczy i gazów istotna jest tylko rozszerzalność objętościowa
- rozszerzalność objętościowa cieczy jest średnio o rząd wielkości większa niż stałych
- gaz znacznie gwałtowniej reagują na zmiany temperatury (i ciśnienia) niż ciała stałe i ciecze.
33. Ciepło przy zmianach temperatury i przy zmianach stanu skupienia
Ciepło Q
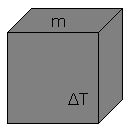
![]()
Po dostarczeniu określonej ilości ciepło Q do ciała o masie m jego temperatura wzrasta o ΔT
![]()
![]()
- ciepło właściwe ciała (bez zmiany stanu skupienia ) ![]()
Uwagi:
-ciepło jest to coś co przenosi się miedzy otoczeniem i układem w wyniku istnienia jedynie różnicy temperatur
-fachowo mówiąc, ciepło jest po prostu jedną z form energii (wyrażoną oczywiście w J) równoważną innym jej formom (energii mechanicznej , elektrycznej …),
-Czasami ciepło (energię) wyraża się w kaloriach (jedna kaloria to ilość ciepła potrzebna do podgrzania 1g wody z 14,5![]()
C do 15,5![]()
C):
1cal = 4,186J
34. Przewodnictwo cieplne
35. I zasada termodynamiki
Wnioski:
- Ciepło Q i praca W to dwie równoważne formy energii, które po dostarczeniu do ciała mogą zmienić jego temperaturę
- Z temperaturą wiąże się pojęcie energii wewnętrznej ciała U [J] (w szczególności dla gazu doskonałego energia wewnętrzna zależy wyłącznie od temperatury (w skali Kelvina) i jest do niej proporcjonalna). Energia wewnętrzna jest miarą energii kinetycznej ruchu cząstek na poziomie mikroskopowym (ruchy postępowe, rotacyjne, oscylacyjne)
I zasada dynamiki:
Zatem zmiana energii wewnętrznej ciała ΔU możliwa jest przy pomocy ciepła Q lub pracy W.
![]()
Ciepło może być dostarczane do układu (+Q) lub czerpane z niego (-Q) podobnie praca może być wykonywana na rzecz układu (+W) lub jego kosztem (-W). Wszystkie te efekty mogą wpłynąć na zmianę energii wewnętrznej układu ΔU
Wyszukiwarka