Wykład 3. Weryfikacja modeli ekonometrycznych

dr Jerzy Zemke

Katedra Ekonometrii

Wydział Zarządzania U.G.

Weryfikacja to sprawdzenie trzech zbiorów założeń o elementach modelu:

1. stopnia zgodności modelu do opisywania przezeń fragmentu rzeczywistości ekonomicznej,

2. określenia kierunku i siły oddziaływania zbioru zmiennych objaśniających na zmienną objaśnianą,

3. weryfikacji założeń o składniku losowym,

4. weryfikacji założeń o stabilności struktury modelu.

Konstrukcja a następnie estymacja parametrów strukturalnych oraz struktury stochastycznej modelu, była możliwa w rezultacie przyjęcia licznego zbioru założeń. Dotyczyły one „oczekiwań” związanych ze zbiorem zmiennych objaśniających, składnika losowego oraz postaci analitycznej relacji pomiędzy zmiennymi objaśniającymi a zmienną objaśnianą. Jest rzeczą oczywistą, że taka konstrukcja formalna definiowana przy tak licznym zbiorze warunków wymaga weryfikacji, która powinna przynieść odpowiedź na fundamentalne pytanie, czy model „potwierdza” przyjęte założenia?

Procedura weryfikacji powinna zatem dać odpowiedź na pytania o poprawność wyboru zbioru zmiennych objaśniających, przyjętego do opisu zmian zmiennej objaśnianej, istotna staje się odpowiedź na pytanie o kierunek oddziaływania zmiennych objaśniających w kontekście zmian zmiennej objaśnianej, wreszcie powinniśmy poznać odpowiedź na pytanie o istotność wpływu zmiennych objaśniających na zmiany zmiennej objaśnianej?.

Chcemy znać także odpowiedź na pytanie, czy przyjęte założenie o postaci analitycznej modelu, nie niesie sprzeczności z „modelowym” opisem zmian zmiennej objaśnianej.

Wprowadzając do modelu składnik losowy, fakt ten tłumaczymy lakonicznie „obiektywną koniecznością”. Mamy świadomość, że należy to przekonywująco uzasadnić a przede wszystkim odpowiedzieć na pytanie, czy składnik losowy jest symetryczny, czy jest losowy, czy jest stacjonarny, czy wartość oczekiwana składnika losowego jest równa zero, czy nie ma miejsca autokorelacja składnika losowego, czy rozkład składnika losowego jest zgodny z rozkładem normalnym?.

Oczekiwania weryfikacji pokazuje schemat, obejmujący wszystkie elementy tego etapu budowy modelu, jak również decyzje, jakie należy podjąć po zakończeniu realizacji każdego etapu procedury w przypadku negatywnej odpowiedzi na pytanie, czy weryfikowany element struktury modelu spełnia nasze oczekiwanie, tzn. czy ma własność którą sprawdzamy, jej nie ma.

Ponadto bez odpowiedzi pozostają pytania o istotność łącznego wpływu zbioru zmiennych objaśniających, istotność zmian zgodności dopasowania modelu w wyniku uzupełnienia bądź usunięcia zmiennych objaśniających, czy pytanie o stabilność struktury modelu.

Schemat procedury weryfikacji założeń przyjętych

w procesie budowy modelu ekonometrycznego.

1. Dopuszczalność modelu ze względu na
.

Niech
model nie jest dopuszczalny ze względu na
}, gdzie
jest wartością „progową” współczynnika determinacji
. Hipotezą alternatywną do
jest hipoteza
model jest dopuszczalny ze względu na
}.

2. Wyrazistość modelu
.

Niech
oznacza udział błędu standardowego
w stosunku do przeciętnej wartości zmiennej objaśnianej
:

.

Weryfikujemy hipotezę
model jest wyrazisty} wobec hipotezy alternatywnej
model jest mało wyrazisty}; gdzie
oznacza wartość krytyczną współczynnika wyrazistości. Wartość krytyczna - „progowa”
, określona w procentach, oznacza jaki najwyższy procent może stanowić błąd standardowy
w stosunku do wartości przeciętnej zmiennej objaśnianej.

3. Istotność parametrów strukturalnych modelu.

Kiedy w początkowej fazie budowy modelu ekonometrycznego przyjmowano założenie o zbiorze zmiennych objaśniających
zmiany zmiennej objaśnianej
, zakładano jednocześnie, że wszystkie zidentyfikowane zmienne objaśniające

wpływają znacząco, w istotny sposób na zmiany zmiennej
.Obecnie założenie to powinno zostać zweryfikowane po to, by stwierdzić, które ze zmiennych istotnie wpływają na zmiany
. W praktyce badań ekonometrycznych oznacza to, że po zakończeniu etapu estymacji parametrów strukturalnych, weryfikujemy hipotezę o istotności ocen, tzn. chcemy znać odpowiedź na pytanie, które parametry istotnie różnią się od zera.

Niech

nie ma istotnego wpływu na zmiany zmiennej
}, hipotezą alternatywną do
jest hipoteza

istotnie wpływa na zmiany
}. Do weryfikacji sformułowanych hipotez posłużymy się statystyką:

,

gdzie:statystyka
ma rozkład
o
stopniach swobody,

- oceny parametrów strukturalnych modelu,

- wartości współczynników przy zmiennych objaśniających dla niektórych i, które a priori są dane /wartości
są równe zero jeśli nie dysponujemy dodatkowymi informacjami o ich wartościach/,

wariancje parametrów
,

- liczba szacowanych parametrów modelu.

Obliczone statystyki
są porównywane z odczytaną z tablic rozkładu
wartością krytyczną /krytyczna wartość sprawdzianu hipotezy/
. Wartość krytyczna ma rozkład
, gdzie poziom istotności
jest prawdopodobieństwem popełnienia błędu w rezultacie którego zostaje odrzucona hipoteza prawdziwa,
jest liczebnością próby statystycznej.

Uwaga:
oznacza tu nie liczbę zmiennych objaśniających lecz liczbę szacowanych parametrów strukturalnych modelu.

Jeżeli
nie ma podstaw do odrzucenia hipotezy
, oznacza to, że zmienna
nie ma istotnego wpływu na zmiany zmiennej
. Jeżeli natomiast
odrzucamy hipotezę
na rzecz hipotezy alternatywnej
, co oznacza, że zmienna
ma znaczący, istotny wpływ na zmiany zmiennej
.

4. Symetria składnika losowego.

Weryfikacja tej własności modelu dotyczy składnika losowego modelu. Poprzednie odnosiły się do założeń o zmiennych objaśniających modelu.

Cechą charakterystyczną poprawnego rozkładu reszt jest symetria rozkładu, rozumiana jako równość prawdopodobieństw /częstości/ występowania dodatnich i ujemnych reszt, czyli:

=
.

Sprawdzając własność symetrii składnika losowego, weryfikujemy hipotezę
, wobec hipotezy alternatywnej
. Statystykę weryfikującą hipotezę
w przypadku dużej próby statystycznej definiujemy następująco:

,

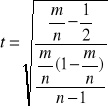
gdzie m jest liczbą dodatnich reszt, a n liczbą wszystkich reszt /liczebność próby/. Rozkład statystyki t jest zbliżony do rozkładu normalnego dla dużej próby statystycznej.

Jeżeli przy założonym poziomie istotności
odczytana z tablic rozkładu normalnego wartość
spełnia nierówność
, to nie ma podstaw do przyjęcia hipotezy
, należy przyjąć hipotezę alternatywną
co z kolei oznacza brak symetrii rozkładu składnika losowego. Jeśli obliczona wartość
nie mamy podstaw do odrzucenia hipotezy
, składnik losowy ma rozkład symetryczny.

W przypadku małej próby statystycznej częstość
ma rozkład dwumianowy o parametrach (p,q), gdzie
. Dla sprawdzenia hipotezy symetrii wystarczy sprawdzić czy zachodzi nierówność:

, gdzie
odczytujemy z tablic 3.1 rozkładu dla
.

Tablica 3.1

5	1	4	18	5	13
6	1	5	19	5	14
7	1	6	20	6	14
8	2	6	21	6	15
9	2	7	22	7	15
10	2	8	23	7	16
11	3	8	24	7	17
12	3	9	25	8	17
13	3	10	26	8	18
14	4	10	27	9	18
15	4	11	28	9	19
16	4	12	29	9	20
17	4	13	30	10	20

Jeżeli warunek
zostaje spełniony, nie ma podstaw do odrzucenia hipotezy
, w przeciwnym przypadku należy uznać hipotezę alternatywną
, co oznacza brak symetrii składnika losowego.

5. Losowość składnika losowego.

Symetryczny rozkład składnika losowego nie jest równoznaczny z losowością rozkładu reszt. Przyczyn takiej sytuacji należy upatrywać w zbyt „długich” seriach reszt o takich samych znakach.

Test serii jest sprawdzianem losowości składnika losowego. Niech A oznacza zdarzenie takie, że

, natomiast B oznacza zdarzenie, że
. Zdefiniujmy ciąg tych zdarzeń według następujących zasad:

1. jeżeli weryfikowany model jest modelem o jednej tylko zmiennej objaśniającej, to:

1. w porządku odpowiadającym rosnącym wartościom tej zmiennej /dane przekrojowe/,

2. w porządku odpowiadającym kolejnym momentom czasu/ szeregi czasowe/,

2. jeżeli weryfikowany model jest modelem o wielu zmiennych objaśniających, a dane stanowią szeregi czasowe, przyjmujemy porządek zdarzeń według kolejnych momentów czasu.

Każdy podciąg ciągu zdarzeń A oraz B, mający tę własność, że zawiera tylko elementy jednego rodzaju A lub B bezpośrednio po sobie następujące, określamy mianem serii. W ciągu może wystąpić kilka serii o jednakowej maksymalnej długości k. Liczbę tych wyróżnionych serii oznaczmy
. Długość serii i liczba serii są zmiennymi losowymi o znanych rozkładach. Rozkłady te stanowią podstawę opracowania tablicy testu serii. Z tablic tych odczytujemy maksymalną liczbę obserwacji n, przy których prawdopodobieństwo spełnienia nierówności:

.

Ta wartość prawdopodobieństwa jest poziomem istotności
przyjętym dla sprawdzenia hipotezy o losowości rozkładu reszt modelu.

Tablica 3.2

Długość serii k	Największa liczba obserwacji n, dla której .
5	10
6	14
7	22
8	34
9	54
10	86
11	140
12	230

Tablica testu serii.

Jeżeli długość serii /maksymalnej/ jest większa od k przy liczebności próby n, to odrzucamy hipotezę
/
składnik losowy jest losowy}/ i przyjmujemy hipotezę alternatywną
/
składnik losowy nie jest losowy}/, w przeciwnym przypadku nie ma podstaw do odrzucenia hipotezy o losowości składnika losowego.

Weryfikacji tej własności składnika losowego można przeprowadzić także przy wykorzystaniu tablic liczby serii. Sprawdzianem hipotezy
jest parametr
określający liczbę wszystkich serii, niezależnie od długości w ciągu reszt. Z tablic liczby serii, dla parametrów rozkładu
, gdzie
oznacza liczbę zdarzeń A,
oznacza liczbę zdarzeń B a parametr
poziom istotności, odczytujemy wartość krytyczną
. Jeżeli
, to nie ma podstaw by przyjąć hipotezę
, oznacza to, że liczba serii uzyskana w próbie jest zbyt mała przyjmujemy hipotezę alternatywną
. Jeśli
, to nie ma podstaw do odrzucenia hipotezy
, co oznacza losowość składnika losowego.

6.Stacjonarność składnika losowego.

Odpowiedź na pytanie o stacjonarność składnika losowego jest jednocześnie weryfikacją założenia o stałości wariancji. Ponieważ stacjonarność rozumiemy jako brak istotnego związku szeregu reszt z czasem, zatem weryfikacja tego założenia, to odpowiedź na pytanie, czy miara takiego powiązania - współczynnik korelacji Pearsona różni się istotnie od zera.

Niech statystyka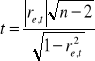
, gdzie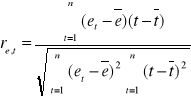
jest sprawdzianem hipotezy
składnik losowy jest stacjonarny} wobec hipotezy alternatywnej
składnik losowy nie jest stacjonarny}. Statystyka t ma rozkład t-Studenta o parametrach
. Z tablic rozkładu t-Studenta odczytujemy wartość krytyczną
. Jeśli
, nie ma podstaw do odrzucenia hipotezy
, jeśli natomiast ma miejsce relacja
, to należy odrzucić hipotezę
, i przyjąć hipotezę alternatywną
, co oznacza brak stacjonarności rozkładu składnika losowego.

W przypadku braku stacjonarności składnika losowego przyczyną może być niewłaściwa metoda estymacji. W takich przypadkach zalecana jest tzw. uogólniona metoda najmniejszych kwadratów. Metoda uogólniona różni się od klasycznej postacią funkcji kryterium dopasowania modelu do danych empirycznych, mianowicie:

,

gdzie
jest ilorazem wariancji składnika losowego w momencie czasu
do wariancji w momencie czasu
.

7. Weryfikacja założenia o wartości oczekiwanej składnika losowego.

Ten etap procedury weryfikacyjnej nie dotyczy modeli liniowych, bowiem metoda najmniejszych kwadratów daje gwarancje nieobciążoności składnika losowego, co wyraża się tym, że jego wartość oczekiwana jest równa zero. Weryfikację tej własności składnika losowego prowadzi się w przypadku modeli sprowadzalnych do postaci liniowej, modeli segmentowych, adaptacyjnych.

Weryfikacji poddajemy hipotezę
wobec hipotezy alternatywnej
. Sprawdzianem hipotez jest statystyka:

, gdzie S jest standardowym błędem oceny.

Statystyka t ma rozkład t-Studenta o (n-1) stopniach swobody. Z tablic rozkładu Studenta dla parametrów rozkładu
określamy wartość krytyczną statystyki
. Jeśli
nie ma podstaw do odrzucenia hipotezy
, jeśli natomiast
nie ma podstaw do przyjęcia hipotezy
, przyjmujemy hipotezę alternatywną
, co oznacza, iż
.

8. Autokorelacja składnika losowego

Analizując ciąg reszt uporządkowanych według wskaźnika czasu, można niekiedy zauważyć, że istnieje zależność reszt z okresu t od reszt przyporządkowanym okresom wcześniejszym. Zależność ta nosi nazwę autokorelacji. Literatura wyróżnia następujące przyczyny wystąpienia autokorelacji:

1. powolne wygasanie tendencji w kształtowaniu się wielkości ekonomicznych /bezwład/,

2. pominięcie istotnych zmiennych objaśniających,

3. przyjęcie błędnego założenia o postaci analitycznej,

4. pominięcie zmiennych opóźnionych w czasie,

5. błędy w ocenie opóźnień czasu niektórych zmiennych objaśniających,

6. „manipulowanie danymi” np. agregacja, bądź interpolacja brakujących informacji statystycznej.

W przypadku zależności pomiędzy szeregami opóźnionymi o jeden okres weryfikujemy hipotezę
wobec hipotezy alternatywnej
. Sprawdzianem jest statystyka:

.

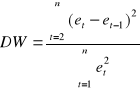
Przekształcając zdefiniowane wyrażenie otrzymamy:

.

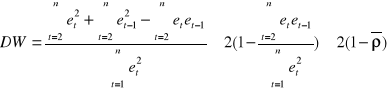
Z definicji współczynnik korelacji
należy przedziału [-1;1] tzn. /
/, zatem statystyka DW należy do przedziału
.

Dla współczynnika korelacji z przedziału [-1,0), obserwujemy ujemną autokorelację, której z reguły odpowiada wartość DW z przedziału (2,4]. Natomiast dla autokorelacji dodatniej, współczynnik
należy do przedziału (0,1], a statystyka DW będzie się zawierała w przedziale [0,2].

W przypadku autokorelacja dodatniej, weryfikujemy hipotezę
wobec hipotezy alternatywnej
. Z tablic rozkładu statystyki Durbina - Watsona dla parametrów rozkładu (n,k) /k oznacza liczbę zmiennych objaśniających/ odczytujemy wartości
oraz
, są to wartości odpowiednio dolna oraz górna wartość krytyczna:

1. jeżeli
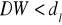
   , hipotezę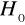
   odrzucamy na rzecz hipotezy alternatywnej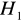
   , oznacza to autokorelację składnika losowego,

2. jeżeli
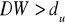
   , nie mamy podstaw do odrzucenia hipotezy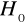
   , oznacza to brak istotnej autokorelacji składnika losowego,

3. jeżeli
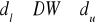
   , nie mamy podstaw do przyjęcia bądź odrzucenia żadnej z dwu hipotez, jest to tzw. obszar niekonkluzywności testu Durbina - Watsona.

Jeśli ma miejsce przypadek autokorelacji ujemnej, korekcie poddajemy wartość statystyki DW, nowa wartość DW' jest różnicą 4-DW. Weryfikujemy hipotezę
, wobec hipotezy alternatywnej
:

4. jeżeli
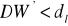
   , hipotezę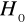
   odrzucamy na rzecz hipotezy alternatywnej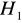
   , oznacza to autokorelację składnika losowego,

5. jeżeli
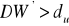
   , nie mamy podstaw do odrzucenia hipotezy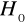
   , oznacza to brak istotnej autokorelacji składnika losowego,

6. jeżeli
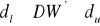
   , nie mamy podstaw do przyjęcia bądź odrzucenia żadnej z dwu hipotez, jest to tzw. obszar niekonkluzywności testu Durbina - Watsona.

Oczywiście możliwe jest także łączne testowanie autokorelacji, bez rozstrzygania jej znaku.

Test Durbina - Watsona stosowany może być wówczas gdy w zbiorze zmiennych objaśniających modelu nie występuje opóźniona w czasie zmienna objaśniana. Jeżeli takie zmienne występują, wówczas w weryfikacji przyjętych hipotez korzystamy z testu - h, pochodzącego od Durbina:

,

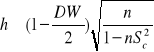
gdzie:
- ocena wariancji współczynnika regresji /parametr strukturalny/ przy
.

Test h ma jedno ograniczenie oczywiście poza tym, że weryfikuje autokorelację rzędu pierwszego, jest nim mianowicie to, że nie możemy wyznaczyć wartości h jeżeli
.

W przypadku autokorelacji rzędu p, w weryfikacji hipotezy o braku autokorelacji rzędu wyższego aniżeli jeden korzystamy z testu Godfreya.

Weryfikujemy hipotezę
autokorelacji rzędu p czyli
}, bowiem zakładamy, że w przypadku hipotezy alternatywnej składniki losowe są generowane przez proces autoregresyjny rzędu p, zapisujemy:

,

gdzie:
- składnik losowy o wartości oczekiwanej
, stałą wariancją
oraz zerowymi kowariancjami
dla
.

Hipoteza alternatywna wobec
przyjmie zatem postać:

miejsce autokorelacja rzędu i, tzn. istnieje takie i, że

Statystyka F ma rozkład Fishera - Snedecora z
stopniami swobody, gdzie
, a
,
oznacza liczbę szacowanych parametrów modelu.

Statystyka zaproponowana przez Godfreya jest równa:

,

gdzie:

,

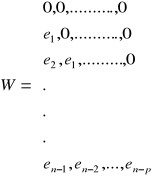
Test Godfreya ma dwa sprawdziany:
, dla dużych prób, oraz
o rozkładzie
dla małych prób. Pomiędzy sprawdzianami testu zachodzi relacja:

.

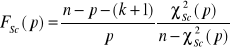
Jeżeli
lub
są większe od wartości krytycznych odczytanych z tablic rozkładu dla ustalonego poziomu istotności i właściwej liczby stopni swobody, nie ma powodów do przyjęcia hipotezy
, należy przyjąć hipotezę alternatywną
, co oznacza istnienie autokorelacji rzędu i. Jeśli zachodzi relacja przeciwna i obliczone statystyki
oraz
są mniejsze od wartości krytycznych odczytanych z tablic rozkładu, nie mamy podstaw do odrzucenia hipotezy
.

9. Normalność składnika losowego.

Podstawową własnością rozkładu normalnego jest symetria oraz mezokurtyczność. Asymetria rozkładu wynika z nierównomierności prawostronnego i lewostronnego rozproszenia, co oznacza, że wartości liczbowe średniej, mediany i dominanty nie pokrywają się.

Standardową miarą asymetrii rozkładu jest współczynnik skośności, określany także mianem współczynnika asymetrii:

;

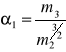
gdzie:
, k=2,3,4,…

Dodatnia wartość
wskazuje na prawostronną asymetrię, natomiast wartość ujemna
na asymetrię lewostronną.

Kurtoza rozkładu wyraża się albo tym, że gęstość rozkładu obserwacji w pobliżu średniej jest większa niż dla rozkładu normalnego, albo tym, że gęstość rozkładu w pobliżu średniej jest mniejsza iż dla rozkładu normalnego. W pierwszym przypadku rozkład cechuje tzw. smukłość, drugi przypadek określamy mianem spłaszczenia rozkładu. Miarą nasilenia kurtozy jest współczynnik kurtozy:

.

Dla rozkładu normalnego, współczynnik kurtozy jest równy
, stąd w praktyce, współczynnik kurtozy definiowany jest jako odchylenie od standardu, czyli

Do weryfikacji hipotez
- rozkład zgodny z rozkładem normalnym} wobec hipotezy alternatywnej
nie ma rozkładu normalnego} korzystamy ze statystyki Jarque'a-Bera
:

Weryfikacja zgodności rozkładu składnika losowego z rozkładem normalnym prowadzona jest na podstawie reszt modelu, stąd:

, j=1,2,3…,

statystykę Jarque'a-Bera można zapisać w postaci równoważnej:

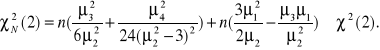
Z tablic testu
dla określonego poziomu ufności
oraz n-2 stopni swobody odczytujemy wartość krytyczną
. Jeśli
, to nie ma powodów do odrzucenia hipotezy
, składnik losowy jest zgodny z rozkładem normalnym, jeśli natomiast
, należy odrzucić hipotezę
i przyjąć hipotezę alternatywną
.

Zweryfikowany zbiór własności elementów struktury modelu dotyczył zarówno zmiennych modelu ale także i to w dużej części składnika losowego. Proces weryfikacji powinien zostać uzupełniony o testy istotności łącznego wpływu zmiennych objaśniających, test na dołączanie i usuwanie zmiennych, weryfikację poprawności założenia o postaci analitycznej oraz testy stabilności struktury modelu weryfikowanej w kontekście stałości oszacowanych parametrów strukturalnych czasie.

10. Istotność łącznego wpływu zmiennych objaśniających.

Definiujemy hipotezę
wobec hipotezy alternatywnej
istnieje takie i, że
. Sprawdzianem hipotezy
jest statystyka:

.

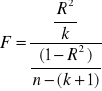
Z tablic rozkładu statystyki F przy określonym poziomie istotności
oraz parametrach rozkładu
, odczytujemy wartość krytyczną statystyki
. Jeśli
, to ma podstaw do odrzucenia hipotezy
, jeśli natomiast
, odrzucamy hipotezę
na rzecz hipotezy alternatywnej
.

11. Test na dołączenie i usuwanie zmiennych.

Budując model ekonometryczny zadajemy sobie pytanie, na ile włączenie dodatkowej zmiennej poprawia dokładność opisu zmian zmiennej objaśnianej. Miarą zgodności czy też dopasowania modelu do danych empirycznych jest współczynnik
. Stąd pytanie, czy uwzględnienie nowej zmiennej w modelu poprawi istotnie stopień dopasowania mierzony współczynnikiem
?.

Niech
, ponadto załóżmy, że stopień dopasowania modelu do danych empirycznych mierzy
/współczynnik determinacji modelu pierwotnego, przed dołączeniem dodatkowej zmiennej objaśnianej/.

Pierwotny zbiór zmiennych objaśniających uzupełnimy o zmienne {
, tzn. ,
miarę dopasowania modelu o tak uzupełniony zbiór zmiennych oznaczmy jako
.

Chcemy zatem zweryfikować hipotezę
wobec hipotezy alternatywnej
istnieje takie j, że k+1
oraz
. Sprawdzianem hipotezy
jest statystyka F:

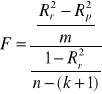
, gdzie m liczba dołączonych zmiennych.

Statystyka F ma rozkład Fishera-Snedecora o parametrach rozkładu
. Z tablic rozkładu statystyki dla poziomu istotności
odczytujemy wartość statystyki
. Jeśli
nie ma podstaw do odrzucenia hipotezy
, jeśli natomiast
, odrzucamy hipotezę
na rzecz hipotezy alternatywnej
, co oznacza, że dołączenie nowej zmiennej powoduje istotne zwiększenia stopnia dopasowania modelu.

12. Poprawność założenia o postaci analitycznej modelu.

Najprostszym rozwiązaniem wątpliwości z tym związanych jest sprawdzenie, czy kwadraty wartości teoretycznych zmiennej objaśnianej nie stanowią „pominiętej zmiennej” w budowanym modelu. Sprawdzamy zatem, czy włączenie dodatkowej zmiennej powoduje istotny wzrost współczynnika determinacji
.

Idea weryfikacji podana została przez Ramseya. Sprawdzian testu ma dwie wersje,
o rozkładzie
oraz wersję
o rozkładzie Fishera-Snedecora
.

Weryfikujemy hipotezę
błąd w założeniu o postaci analitycznej} wobec hipotezy alternatywnej
poprawna postać analityczna}. Z tablic rozkładu
bądź rozkładu statystyki F odczytujemy wartości krytyczne obydwu statystyk, statystykę
weryfikujemy identycznie jak w teście Godfreya.

13. Stabilność parametrów strukturalnych modelu.

Po oszacowaniu parametrów strukturalnych modelu, ciekawe staje się pytanie, czy oszacowane parametry nie zmieniają się w czasie? To ważne pytanie, bowiem od stałości parametrów zależy wiarygodność konstruowanych prognoz zmian zmiennej objaśnianej w przyszłości.

W 1960 r. Chow podał sprawdzian stabilności parametrów modelu. Należy dokonać podziału próby na dwa podzbiory
oraz
takie, że
.

Zatem model możemy zapisać:

,

Weryfikujemy hipotezę
wobec hipotezy alternatywnej
. Sprawdzianem hipotezy
jest statystyka
dla dużych prób i statystyka
dla prób małych.

,

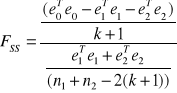
gdzie:
- wektor reszt modelu szacowanego MNK na podstawie całej próby n,

- wektor reszt modelu szacowanego MNK na podstawie próby n₁,

- wektor reszt modelu szacowanego MNK na podstawie próby n₂.

Przy założeniu, że wariancje składnika losowego w obydwu „podpróbach” są sobie równe, statystyka
ma rozkład Fishera-Snedecora o (
stopniach swobody a statystyka:

, ma rozkład
.

Z tablic rozkładu statystyk F oraz
odczytujemy wartości krytyczne. Jeśli statystyki obliczone są mniejsze lub równe wartościom krytycznym statystyk, to nie ma powodów by przyjąć hipotezę
, w przeciwnym przypadku uznajemy hipotezę alternatywną
, co oznacza, że parametry strukturalne nie są stabilne w czasie.

1.Dopuszczalność modelu ze względu na

Tak

Nie

Nie

Tak

2.Wyrazistość modelu V

3.Istotność parametrów strukturalnych

Nie

Tak

4.Symetria składnika losowego

Nie

Tak

5.Losowość składnika losowego

Nie

Tak

6.Stacjonarność składnika losowego

Nie

Tak

7.Weryfikacja założenia o wartości oczekiwanej składnika losowego

Nie

Tak

8.Badanie braku autokorelacji składnika losowego

Tak

Nie

9.Normalność rozkładu składnika losowego

Nie

Tak

I. Ustalenie zbioru zmiennych relacji opisujących badaną prawidłowość

II. Przyjęcie założeń o postaci analitycznej zdefiniowanych relacji

III. Estymacja parametrów strukturalnych modelu

IV. Weryfikacja założeń przyjętych w etapach I,II,III

V. Predykcja ekonometryczna, konstrukcja prognoz

---