MECHANIKA

Mechanika - dział fizyki mówiący o ruchu ciał materialnych pod wpływem działających sił.

Podstawowe pojęcia mechaniki to:

1. Punkt materialny.

2. Układ punktów materialnych.

3. Bryła sztywna.

Ad1. Punktem materialnym - nazywamy punkt geometryczny, który posiada pewną skończoną masę.

Ad2. Układem punktów materialnych - nazywamy zbiór punktów materialnych.

Ad3. Bryłą sztywną - nazywamy układ punktów, w którym wzajemne odległości nie ulegają zmianie.

Pojęcia pierwotne w mechanice:

Przestrzeń - jest to wielkość związana z określeniem położenia punktu lub ciała.

Czas - II wielkość pierwotna

Masa - miara służąca do scharakteryzowania i do porównania ciał materialnych w oparciu o podstawowe eksperymenty

Siła - jest miarą oddziaływania jednego ciała na drugie po przez kontakt bezpośredni obu ciał, bądź na odległość ( pola magnetyczne ).

Mechanika Newtonowska - wielkości niezależne

Mechanika realistyczna - wielkości zależne przy dużych prędkościach

Mechanika klasyczna - zajmuje się badaniem warunków spoczynku i ruchem punktów materialnych i brył sztywnych w funkcji czterech pojęć podstawowych.

Podział wielkości fizycznych:

- skalary,

- wektory.

Skalar - to wielkość, którą można określić za pomocą jednej liczby rzeczywistej ( np. czas, masa, energia, praca, moc, gęstość ).

Wektor - jest to wielkość określona liczbą, posiadająca kierunek i zwrot w przestrzeni ( np. siła, prędkość, przyspieszenie ). Obrazem wektora jest odcinek skierowany.

Określając wektor należy podać:

- Wartość ( moduł wektora ) - stanowi liczbę jednostek długości narysowanej w przyjętej skali - oznaczenie:

- Kierunek ( wyznacza prosta „l” )

- Zwrot ( zaznaczony grotem )

Oznaczenie wektora:

Pojęcie siły można określić jako wzajemne oddziaływanie jednego ciała na drugie. Jest wielkością wektorową gdyż dla jednoznacznego opisania należy określić:

1. Wartość liczbową - długość odcinka CD.

2. Kierunek - który wyznacza prosta „l”.

3. Zwrot - oznaczony grotem.

Punkt D ( punkt zetknięcia wektora siły z ciałem ) nazywamy punktem przyłożenia siły.

Układ sił - jest to zbiór sił przyłożonych w jednym lub kilku punktach ciała.

Podział sił ( na sposób przyłożenia ):

• siła skupiona,

• siła powierzchniowa,

• siła objętościowa lub masowa.

Siła skupiona - jest to sił, która działa na ciało materialne w pewnym określonym punkcie.

Siły powierzchniowe - są to siły, których działanie jest rozłożone na części lub na całej powierzchni ( np. siła nacisku jednego ciała położonego na drugie, siła wiatru napierającego na ścianę budynku ).

Siły objętościowe lub masowe - są to siły, których działanie jest rozłożone na całą objętość ciała.

Podział sił:

• siły wewnętrzne,

• siły zewnętrzne:

- siły czynne,

- siły bierne.

Siły zewnętrzne - są to siły oddziaływania pomiędzy poszczególnymi ciałami lub bryłami sztywnymi, źródłem działania tych sił są inne ciała.

Siły zewnętrzne czynne - są to takie siły, które próbują zmienić stan spoczynkowy lub ruchowy ciała.

Siły zewnętrzne bierne - występują w miejscach ograniczających swobodę ruchu ciała w tzw. podporach, występują one podczas działania sił zewnętrznych czynnych przeciwdziałając ruchowi.

Siły wewnętrzne - siły oddziaływania pomiędzy cząsteczkami materii tego samego ciała po dokonaniu „myślowego” przecięcia przez ciało.

DEF. MOMENTU SIŁY WZGLĘDEM PUNKTU: Momentem siły względem punktu ( nazwanego punktem „O” ) nazywamy wektor momentu
_O równy iloczynowi wektorowemu promienia
wyprowadzonego z punktu O do wektora
i wektora siły
.

_O
=

Jego kierunek (
_O ) jest prostopadły do płaszczyzny utworzonej przez wektory
i
.

Jego wartość jest równa
=Fd.

Zwrot
_O zgodny z regułom śruby prawoskrętnej.

PRAWA NEWTONA

I Prawo Newtona. Jeżeli na ciało nie działają żadne siły lub działające siły równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym po lini prostej.

II Prawo Newtona. Jeżeli na ciało działa siła ( wypadkowa wszystkich sil działających na punkt materialny jest różna od zera ), to porusza się ono względem inercjalnego układu odniesienia ruchem zmiennym z przyspieszeniem wprost proporcjonalnym do siły, a odwrotnie proporcjonalnym do masy ciała. Kierunek i zwrot wektora przyspieszenia są zgodne z kierunkiem i zwrotem wektora siły.

III Prawo Newtona. Jeżeli dwa ciała A i B działają wzajemnie na siebie, to siła
_AB, z jaką ciało A działa na ciało B i siła
_BA, z jaką ciało B działa na ciało A, są równe co do wartości, mają ten sam kierunek, ale przeciwne zwroty.

_AB= ­ -
_BA

Prawo Grawitacji Newtona. Każde dwa punkty materialne przyciągają się wzajemnie siłą wprost proporcjonalną do iloczynu ich mas i odwrotnie proporcjonalną do kwadratu odległości między nimi.

₁₂=g

- wektor jednostkowy, g - stała grawitacji

ZASADY STATYKI

Zasada pierwsza ( zasada równoległoboku ) - działanie dwóch sił P1 i P2 można zastąpić działaniem jednej siły R, działającej na ten sam punkt i będącej przekątną równoległoboku ABCD zbudowanego na wektorach sił P1 i P2.

Gdy siły P1 i P2 działają wzdłuż jednej prostej i są zgodnie skierowane R=P1+P2.

Natomiast, gdy siły są przeciwnie skierowane i P2>P1; R=P2-P1.

Zasada druga - jeżeli do ciała przyłożone są dwie siły, to równoważą się one tylko wtedy gdy mają te samą linię działania, te same wartości liczbowe i przeciwne zwroty. Aby siły te równoważyły się, muszą być spełnione zależności:
i
. Na podstawie tej zasady można, wyprowadzić pojęcie siły zerowej, czyli siły, której wartość jest równa zeru. Z zasady tej wynika także pojęcie siły przeciwnej do siły P1, której bezwzględna wartość oraz linie działania są takie same, ale zwrot jest przeciwny. Siłę przeciwną oznacza się znakiem minus ( -P2 ).

Zasada trzecia - skute działania układu sił przyłożonego do ciała nie zmienia się, jeśli do tego układu dodamy lub odejmiemy dowolny układ równoważących się sił, czyli tzw. układ zerowy. Z zasady tej wynika następujący wniosek: każdą siłę działającą na ciało sztywne można przesunąć dowolnie wzdłuż jaj lini działania.

Zasada czwarta ( zasada zesztywnienia ) - jeżeli ciało odkształcalne znajduje się w równowadze pod działaniem pewnego układu sił, to również pozostanie w równowadze ciało odkształcalne sztywne ( nieodkształcalne ) identyczne z poprzednim, pod działaniem tego samego układu sił. Wynika stąd wniosek, że warunek konieczny i wystarczający do równowagi ciała sztywnego jest tylko warunkiem koniecznym, ale nie wystarczającym do równowagi ciała odkształcalnego.

Zasada piąta ( zasada działania i przeciwdziałania ) - każdemu działaniu towarzyszy równe co do wartości, o przeciwnym zwrocie i leżące na tej samej prostej przeciwdziałanie.

Zasada szósta ( zasada oswobodzenia od więzów ) - każde ciało nie swobodne można myślowo oswobodzić z więzów, zastępując ich działanie reakcjom, a następnie rozważać jako ciało swobodne znajdujące się pod działaniem sił czynnych i biernych ( reakcji więzów ).

Własności iloczynu skalarnego:

• przemienność:
  

• rozdzielność względem dodawania:
  

• łączność mieszana:
  

• warunek prostopadłości wektorów:
  

Własności iloczynu wektorowego:

• antyprzemienność:
  

• rozdzielność względem dodawania:
  

• łączność mieszana:
  

• prostopadłość iloczynu wektorowego do pozostałych czynników:
  =0

Zwrot zgodny z regułą Zwrot przeciwny do reguły

śruby prawo skrętnej śruby prawo skrętnej

znak „+” znak „ - ”

Moment siły względem punktu nie zmieni się jeżeli siłę przeniesiemy wzdłuż jej lini działania.

Jeżeli prosta działania siły przechodzi przez punkt O to moment siły równa się zero.

Moment siły w kartezjańskim układzie współrzędnych.

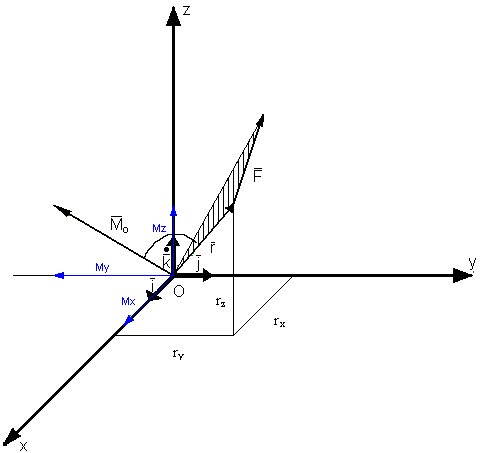
M_x, M_y, M_z - moment siły względem danej osi

,
,
- wektory jednostkowe

Po rozwinięciu wyznacznika współrzędne, które nazywamy momentami siły względem odpowiedniej osi nazywamy:

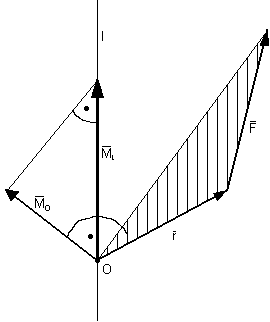
Moment siły względem osi jest równy zero, gdy siła jest równoległa do osi lub gdy linia działania siły przecina oś.

Moment siły
względem punktu o jest sumą, momentów sił względem osi: x, y, z przecinających się w tym punkcie.

Momentem siły
względem dowolnej prostej l nazywamy rzut, wektora momentu obliczanego względem dowolnego punktu leżącego na prostej l, na prostą l.

( rys. obok )

Zmiana bieguna ( punktu O ) momentu siły.

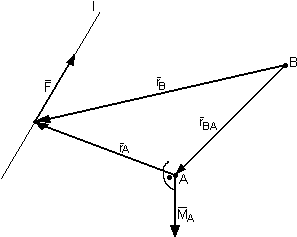
Moment względem punktu A:

Moment względem punktu B:

Patrz rysunek - dodawanie wektorów metodą trójkąta:

Moment siły względem punktu B jest równy sumie dwóch momentów, z których jeden obliczany jest względem dowolnego punktu, natomiast drugi jest momentem tej siły uczepionym w punkcie A liczonym względem punktu B.

Twierdzenie Varignona. Moment sumy sił względem dowolnego punktu jest równy sumie momentów poszczególnych sił względem tego punktu.

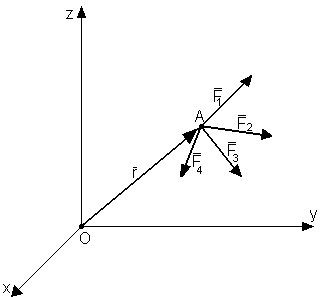
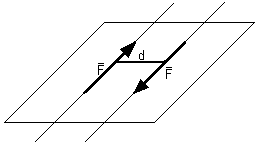
Para sił i jej własności. Układ dwóch sił równoległych o takich samych wartościach liczbowych lecz przeciwnie zwróconych nazywamy parą.

d - ramię pary sił

Wypadkowa pary sił równa się zero, czyli pary sił nie można zastąpić jedną siłą.

Oddziaływanie pary sił wyraża się momentem pary sił.

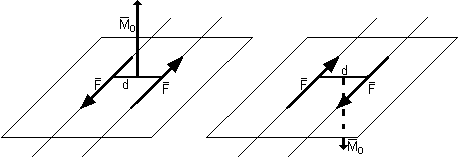
Momentem pary sił - jest wektor prostopadły do płaszczyzny działania pary sił, o wartości równej iloczynowi wartości siły i ramienia, o zwrocie zgodnym z regułą śruby prawo skrętnej.

Własności pary sił:

I Dwie pary sił o tej samej płaszczyźnie działania są sobie równe, gdy posiadają równe momenty.

Dowód pierwszej własności:

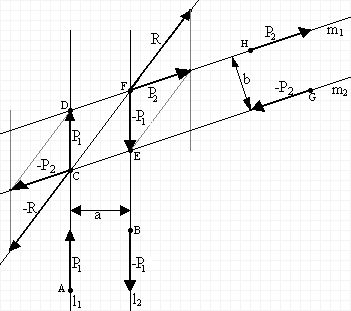
Na rysunku przedstawiono parę sił P₁ i P₂ o liniach działania l₁ i l₂, których moment: M₁=P₁a.

Prowadząc dwie dowolne proste m₁ i m₂, otrzymamy punkty C, D, E, F. Siły P₁ i -P₁ przyłożone do punktów A i B możemy przesunąć do punktów C i F. Na prostej przechodzącej przez punkty C i F przykładamy układ sił R i -R równy zeru. Po złożeniu sił P₁ i -R oraz -P₁ i R otrzymamy siły wypadkowe P₂ i -P_2. Z równości obu równoległoboków sił, zbudowanych w punktach C i F, wynika że siły P₂ i -P₂ tworzą parę sił równoważną parze sił P₁ i -P₁, bo różnią się tylko o układ równoważny zeru: M₂=P₂b=P₁a=M₁

II Zachowując niezmieniony moment, parę sił można przenieść do dowolnej płaszczyzny równoległej do jej płaszczyzny działania nie zmieniając równowagi układów.

Dowód drugiej własności:

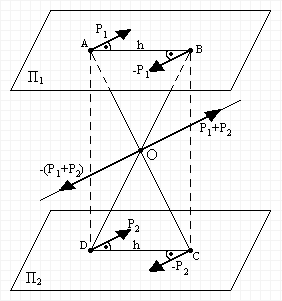
Mamy parę sił P₁ i -P₁ w odległości h, leżącą na płaszczyźnie ∏₁. Na płaszczyźnie równoległej ∏₂ do ∏₁ umieszczamy dwa układy równoważne zeru sił P₂ i -P₂ w tej samej odległości h. Zakładamy, że siły P₂ i -P₂ są równe sile P₁. wypadkowa sił jednakowo zwróconych P₁ i P₂ wynosi ( P₁ + P₂ ) i przyłożona jest w punkcie O. Podobnie wypadkowa sił -P₁ i -P₂ równa się sile wypadkowej -( P₁ + P₂ ) i przy łożona jest także w punkcie O. Siły wypadkowe równoważą się, tworząc w punkcie O układ równoważny zeru. Z całego układu pozostaną, wówczas siły P₂ i -P₂ tworząc parze sił równoważną parze sił P₁ i -P₁. otrzymaną parę sił P₂ i -P₂ możemy na podstawie pierwszego twierdzenia zastąpić w płaszczyźnie ∏₂ dowolną, inną parą sił o tym samym momencie.

III Dwie pary sił działające w jednej płaszczyźnie można zastąpić przez jedną parę sił, działającą w tej samej płaszczyźnie o momencie równym sumie momentów dwóch par sił.

Dowód trzeciej własności:

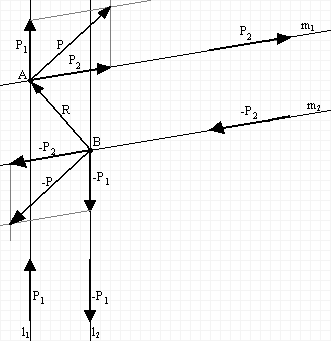
Mamy dwie pary sił P₁ i -P₁ oraz P₂ i -P₂. siły wchodzące w skład tych par możemy przesunąć wzdłuż ich linii działania l₁ i l₂ oraz m₁ i m₂ do punktów A i B. Po złożeniu sił P₁ i P₂ oraz -P₁ i -P₂ otrzymamy wypadkowe P i -P.

P=P₁+P₂ -P=-P₁-P­₂

Stąd wynika, że siły P i -P stanowią parę sił. Jest to para stycznie równoważna układowi par ( P₁, -P₁ ) i ( P₂, -P₂ ), ponieważ powstała z tych par przez zastosowanie zasad statyki. Po oznaczeniu przez M₁, M₂, M momentów par ( P₁, -P₁ ), ( P₂, -P₂ ) i ( P, -P ) oraz
:

IV Dwie pary sił działające w przecinających się płaszczyznach są równoważne jednej parze sił o momencie równym wektorowej sumie momentów tych par.

Dowód czwartej własności:

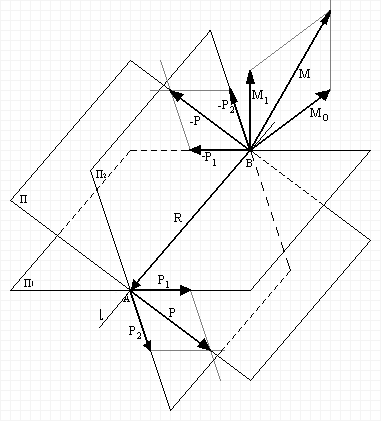
Mamy dwie pary sił ( P₁, -P₁ ) i ( P₂, -P₂ ), o momentach M₁ i M₂, działające odpowiednio w płaszczyznach ∏₁ i ∏₂ , przecinające się wzdłuż prostej l. Przyłożone do punktu A siły P₁ i P₂ zastępujemy wypadkową P, a siły -P₁ i -P₂ wypadkową -P.

P=P₁+P₂ -P=-P₁-P₂

Co oznacza, że siły P i -P stanowią parę równoważną układowi dwóch par ( P₁, -P₁ ) i ( P₂, -P₂ ). Oznaczając moment pary sił ( P, -P ) przez M oraz
:

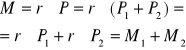
Twierdzenie o równoległym przesunięciu sił.

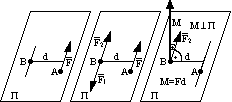
Do punktu B przykładamy siły zerowe F₁ i F₂, siła F₁ równoważy siłę F.

Płaski dowolny układ sił.

Płaskim układem sił - nazywamy taki układ, w którym siły zewnętrzne czynne i bierne leżą w jednej płaszczyźnie.

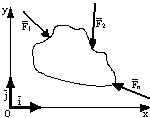
Warunki równowagi dowolnego układu sił.

Dowolny płaski układ sił jest w równowadze jeśli algebraiczne sumy wszystkich rzutów sił na osie układu i suma momentów wszystkich sił względem dowolnie obranego bieguna na płaszczyźnie działania tych sił są równe zeru.

Punkty ABC nie mogą leżeć na jednej linii.

Szczególny przypadek: warunki równowagi płaskiego zbieżnego układu sił.

Układem sił zbieżnych - nazywamy układ, w którym linie działania się przecinają się w jednym punkcie.

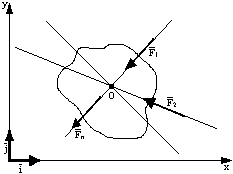
Siły zbieżne leżące w jednej płaszczyźnie są w równowadze jeżeli sumy rzutów tych sił na dwie osie prostokątnego układu współrzędnych są równe zero.

Płaski układ sił równoległych.

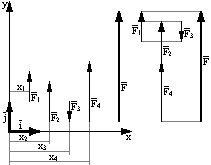
Poszczególne siły rzutujemy na oś y, powstaje siła F, która musi spełnić:

Geometryczne warunki równowagi układów sił na płaszczyźnie.

Równowaga trzech sił na płaszczyźnie. Trzy siły leżące na jednej płaszczyźnie są w równowadze w tedy gdy kierunki działania tych sił przecinają się w jednym punkcie, siły zaś tworzą trójkąt zamknięty o zgodnym obiegu strzałek.

Równowaga czterech sił na płaszczyźnie. Cztery siły leżące na płaszczyźnie są w równowadze wtedy gdy wypadkowe par sił wchodzących w skład czwórki sił mają te same wartości, przeciwne zwroty i leżą, na prostej działania łączącej punkty przecięcia par sił.

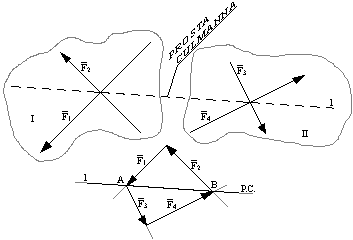
Kierunki par sił muszą się przecinać, Prosta Culmanna ( domniemana siła ) dla sił F₁, F₂ ma zwrot AB, a dla sił F₃, F₄ zwrot BA.

Rodzaje podpór:

1. Podpora przegubowa przesuwna:

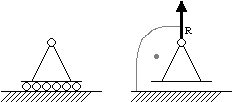
Jedna niewiadoma reakcja R.

2. Podpora przegubowa stała:

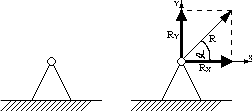
Dwie niewiadome reakcje R_x i R_y ( lub R i α )

3. Zawieszenie na cięgnach wiotkich:

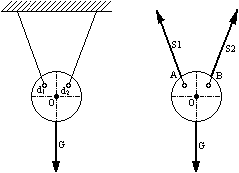
Dwie niewiadome S₁ i S_2­

4. Podparcie na gładkiej lub chropowatej powierzchni:

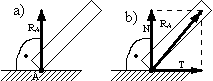
a) więzły idealne

b) więzły normalne ( z tarciem )

5. Utwierdzenie sztywne:

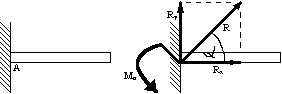
Trzy niewiadome R_x, R_y i Mo ( moment utwierdzenia )

6. Pręt przegubowy:

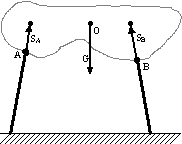
Po jednej niewiadomej na każdy pręt

Zastosowanie metody wieloboku sznurowego do redukcji płaskiego układu sił.

Dane są trzy siły P₁, P₂, P₃ działające w jednej płaszczyźnie, wzdłuż prostych l₁, l₂ i l₃.

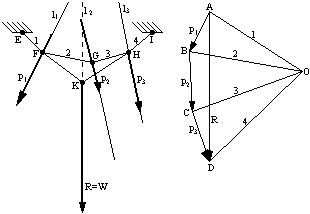
Jeżeli chcemy znaleźć wypadkową W tych sił, to należy zbudować wielobok ABCD. Wartość i kierunek wypadkowej określa zamykający bok AD ( wektor główny R ) wieloboku sił. Pozostaje jeszcze kreślić w planie sił punkt, przez który przechodzi linia działania tej wypadkowej. W tym celu w wieloboku sił obieramy dowolny punkt O, zwany biegunem, i łączymy go promieniami 1, 2, 3, 4 z początkiem i końcem każdej z sił P₁, P₂, P₃. jak wynika z wieloboku sił, na trzy siły przypadają cztery promienie. W ogólnym przypadku na n sił przypada n+1 promieni. Przy tym sposobie oznaczenia promień 1 łączy biegun O z wierzchołkiem wieloboku sił, w którym znajduje się początek siły P1, następnie promień 2 łączy biegun O z wierzchołkiem wieloboku sił, w którym znajduje się początek siły P₂ itd.

W planie sił z dowolnego punktu F, położonego na prostej l₁ ( linia działania siły P₁ ), prowadzimy proste równoległe do promieni 1 i 2. Prosta równoległa do promienia 2 przecina prostą l₂ ( linię działania siły P₂ ) w punkcie G. Z tego punktu prowadzimy prostą równoległą do promienia 3, aż do przecięcia się z prostą l₃ ( linia działania siły P₃ ) w punkcie H, z którego prowadzimy prostą równoległą do promienia 4.

Sposób rysowania prostych równoległych planie sił jest taki, że każdemu trójkątowi ( P₁, 1, 2 ) w wieloboku sił odpowiada w planie sił węzeł F, w którym przecina się linia działania siły P₁ z prostymi równoległymi do promieni 1 i 2. ostatecznie otrzymujemy w planie sił linię łamaną EFGHI ( 1, 2, 3, 4 ), nazwaną wielobokiem sznurowym. Następnie rozkładamy każdą z sił P₁, P₂, P₃ na składowe wzdłuż wieloboku sznurowego. Tak więc siłę P₁ rozkładamy na S₁ i S₂, siłę P₃ na składowe S₃ i S₄. Wielkości i zwroty tych składowych odczytujemy z wieloboku sił, gdzie P₁=S₁+S₂, P₂=S₂'+S₃, P₃=S₃'+S₄, S₂'=-S₂, S₃'=-S₃.

W ten sposób dany układ sił ( P₁, P₂, P₃ ) zastępuje się równoważnym mu statycznie układem sił ( S_1, S₂, S₂', S₃, S₃', S₄ ). Ale siły S₂ i S₂' oraz S₃ i S₃' ( jako parami równe co do wartości i przeciwnie skierowane ) równoważą się wzajemnie. Pozostają jedynie siły S₁ i S₄ działające wzdłuż skrajnych boków 1 i 4 wieloboku sznurowego. Wypadkowa W sił S₁ i S₄ jest równocześnie wypadkową sił P₁, P₂ i P₃, a jej linia działania - prosta l - przechodzi w planie sił przez punkt K przecięcia boków 1 i 4 wieloboku sznurowego i jest równoległa do wektora głównego R ( boku AD wieloboku sił ). Podobnie wyznacza się wypadkową dowolnej liczby sił działających w jednej płaszczyźnie ( oczywiście przy założeni, że wypadkowa istnieje ).

Na podstawie dotychczasowych rozważań możemy stwierdzić, że:

Dowolny płaski układ sił można zastąpić przez dwie siły, działające wzdłuż skrajnych boków wieloboku sznurowego. Wartości tych sił są wyrażone przez długości odpowiednich promieni wieloboku sił, a zwroty są takie, że wektorowa suma tych sił jest równa wektorowi głównemu R. Linia działania wypadkowej W=R przechodzi przez punkt przecięcia skrajnych boków wieloboku sznurowego.

Korzystając z tych spostrzeżeń, możemy przy określaniu wypadkowej płaskiego układu sił nie wyznaczać sił składowych S_1, S₂, S₂', S₃, S₃', S₄ ..., itd., które wyznaczaliśmy w celu wyjaśnienia konstrukcji wieloboku sznurowego.

Na poniższym rysunku przedstawiono sposób określania wypadkowej czterech sił działających w jednej płaszczyźnie. Wartości wypadkowej i jej kierunek określa zamykający bok AE wieloboku ABCDE, a jej linia działania przechodzi przez punkt K, będący punktem przecięcia się skrajnych boków wieloboku sznurowego 1 i 5.

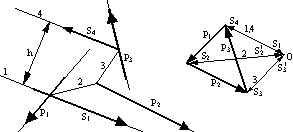
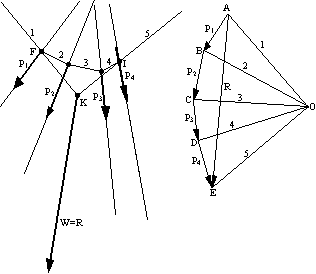
W dotychczas rozważanych przykładach układy sił redukowały się do siły wypadkowej, gdyż odpowiadające im wieloboki sił nie zamykały się. Weźmy teraz pod uwagę przypadek, gdy wektor główny R jest równy zeru, tzn., że wielobok sił jest zamknięty i ma zgodny obieg wektorów sił P₁, P₂, P₃. W przypadku pierwszym ( obok, prawa ) układ sił sprowadza się do pary sił S₁ i S₄. Ramię h tej pary jest równe odległości między skrajnymi bokami wieloboku sznurowego i i 4.

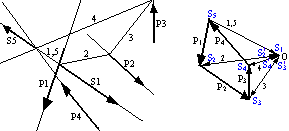
W przykładzie drugim ( obok, lewo ) siły S₁ i S₅ równoważą się, gdyż pierwszy bok wieloboku sznurowego 1 pokrył się z ostatnim 5, co oznacza, że układ sił ( P₁, P₂, P₃, P₄ ) jest w równowadze.

Przy redukcji płaskiego układu sił mogą występować następujące przypadki:

1. Wielobok sił nie zamyka się - układ sił                                                                       redukuje się do jednej siły wypadkowej.

2. Wielobok sił zamyka się, a wielobok sznurowy nie zamyka się - układ sił redukuje się do pary sił.

3. Wielobok sił zamyka się i wielobok sznurowy również się zamyka - układ sił znajduje się w równowadze.

Dowolny układ sił w przestrzeni.

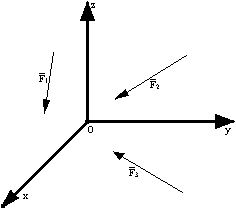
Przestrzennym układem sił - nazywamy układ o dowolnie rozmieszczonych w przestrzeni liniach działania.

Warunki równowagi dowolnego przestrzennego układu sił.

Przestrzenny dowolny układ sił znajduje się w równowadze jeżeli algebraiczne sumy rzutów wszystkich sił na trzy osie układu współrzędnych i algebraiczne sumy momentów wszystkich sił względem tych osi są równe zero.

Równania równowagi:

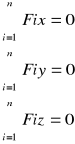
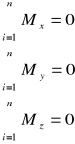
Przestrzenny układ sił zbieżnych:

Przestrzenny układ sił zbieżnych - znajduje się w równowadze gdy sumy rzutów wszystkich sił na trzy osie prostokątnego układu współrzędnych są równe zero.

Równania równowagi:

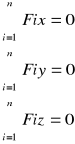
Przestrzenny układ sił równoległych:

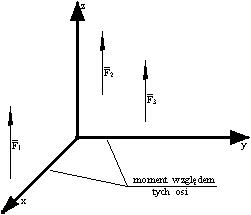
Warunki równowagi przestrzennego układu sił równoległych - suma rzutów sił na oś równoległą do kierunku działania sił jest równa zero oraz równania momentów względem osi leżących na płaszczyźnie prostopadłej do kierunku działania sił są równe zero.

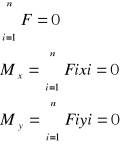
Sposoby podparcia w układach przestrzennych:

1. Przegub kulisty.

2. Łożysko szyjne.

3. Łożysko oporowe lub stopowe.

4. Zawias.

5. Usztywnienie całkowite.

Redukcja dowolnego układu sił.

Przez redukcję układu sił rozumiemy przekształcenie układu w możliwie najprostszy.

Elementy redukcji dowolnego płaskiego układu sił:

- wektor główny F_g,

- moment główny M_g,

- parametr układu tzw. wyróżnik k ( p ).

Wektor główny - równy jest sumie geometrycznej wszystkich sił układu traktowanych jako wektory swobodne. Wektor główny nie zależy od bieguna do którego redukujemy układ sił.

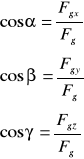
Moment główny ( ogólny ) - równy jest sumie momentów wszystkich sił względem bieguna redukcji O. Moment główny zależy od wyboru bieguna.

Parametr układu ( wyróżnik ) - to iloczyn skalarny wektora głównego i momentu ogólnego.

, czyli:
k≤0

Przypadki redukcji dowolnego układu sił.

WEKTOR GŁÓWNY	MOMENT GŁÓWNY	PARAMETR UKŁĄDU k	WYNIK REDUKCJI
=0	=0	=0	UKŁĄD W RÓWNOWADZE
=0	≠0	=0	PARA SIŁ
≠0	=0	=0	WYPADKOWA
≠0	≠0	≠0	( )SKRĘTNIK, DWIE SIŁY SKOŚNE

Redukcja dowolnego przestrzennego układu sił do skrętnica.

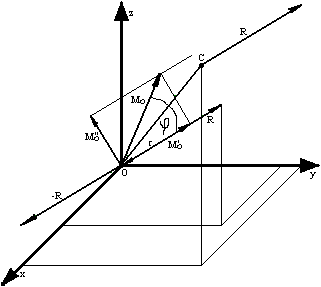
Układ wektora głównego R i momentu głównego M_go, obliczonego względem środka redukcji O, spróbujmy zredukować do prostszej postaci. Niech wektory R i M_o będą przyłożone w punkcie O, początku układu współrzędnych.

Rozłóżmy moment główny M_o na dwie składowe: M'_o - zgodną z kierunkiem wektora głównego R i M''_o - prostopadłą do tego wektora. Następnie składową M''_o zastępujemy parą sił ( -R, R ), leżącą w płaszczyźnie prostopadłej do M''_o, przy czym siła ( -R ) jest przyłożona w punkcie O. Linia działania drugiej siły R będzie przechodzić przez pewien szczególny punkt, którego położenie jest opisane promieniem - wektorem r, wynikającym z następującej zależności:
, która określa równoważność zastępowania wektora M''_o parą sił ( -R, R ). W wyniku tych przekształceń otrzymaliśmy dwie siły ( -R, R ), przyłożone w punkcie O, które można usunąć jak układ równoważący się. Cały układ redukuje się wówczas do siły R przyłożonej do punktu głównego M'_o równoległej do R.
, gdzie
- wektor jednostkowy ( wersor ) o kierunku i zwrocie wektora R, natomiast cosφ - cosinusem kąta między wektorami R a M_o.

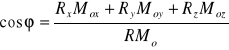
. Ponieważ wektor M'_o jest wektorem swobodnym, więc można go przenieść do punktu C.

Tak więc wykazaliśmy, że dowolny przestrzenny układ n sił można zredukować do dwóch wektorów kolinearnych: wektora głównego R, określanego wzorem
i wektora M'_o, określanego zależnością
. Taki prosty układ tych wektorów nazywa się skrętnikiem, a ich linia działania, przechodząca przez punkt C, nazywa się osią centralną układu sił Pi.

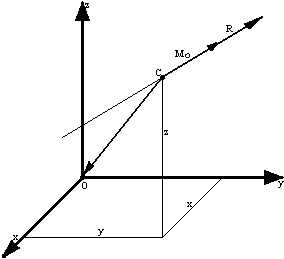
Układ złożony z wektora głównego i składowej momentu głównego M'_o, leżącej na linii działania wektora R, nazywamy skrętnikiem.

Równanie osi centralnej wyznaczamy, redukując wektor główny R i moment główny M_o ( obliczony względem środka redukcji O ) do innego środka redukcji, którym jest punkt C. Moment główny M_c względem punktu C, opisanego promieniem wektorem r o składowych ( -x, -y, -z ) na podstawie wzory
wynosi:

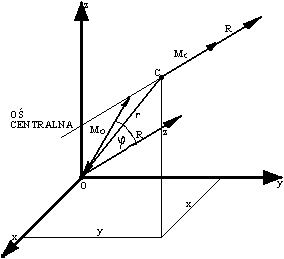
stąd otrzymujemy składowe wektora głównego M_c:

M_cx=M_ox-R_zy+R_yz

M_cy=M_oy-R_zx-R_xz

M_cz=M_oz-R_yx+R_xy

Ponieważ punkt C leży na osi centralnej, więc M_c= M'_o. Wówczas wektory R i M_c, jako kolinearne, muszą być wzajemnie proporcjonalne, czyli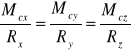
, a po podstawieniu wyrażeń ( M_cx, M_cy, M_cz ) otrzymamy ostatecznie:

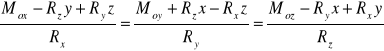
, związki te przedstawiają dwa niezależne równania liniowe z trzema niewiadomymi ( x, y, z ), będące równaniem osi centralnej układu sił. Prosta ta ma takie same cosinusy kierunkowe jak wektor główny układu R.

Redukcja dowolnego przestrzennego układu sił do siły wypadkowej.

Szczególny przypadek redukcji przestrzennego układu sił otrzymujemy, gdy wektor momentu głównego M_o, obliczony względem dowolnego punktu O, będzie prostopadły do wektora głównego R.

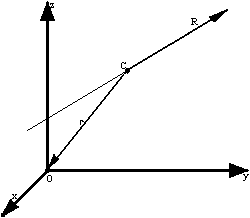
Składowa momentu głównego M'_o ( według pierwszego rysunku do redukcji do skrętnika ) będzie równa zeru i układ redukuje się wyłącznie do sumy geometrycznej R, przechodzącej przez punkt C. Oznacza to, że taki układ sił Pi daje się zredukować wyłącznie do jednej siły R, która jest wypadkową układu sił, leżącą na osi centralnej układu. W tym przypadku oś centralna staje się linią działania wypadkowej ( rysunek po prawej ).

Warunkiem koniecznym i dostatecznym, aby przestrzenny układ sił Pi redukował się do wypadkowej, jest istnienie różnej od zera sumy geometrycznej R i prostopadłości wektora momentu głównego M_o­ względem dowolnie wybranego punktu O do linii działania sumy geometrycznej.

Przykład:

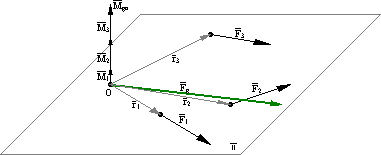
Wektor główny jest niezmiennikiem - nie zależy od bieguna redukcji.

- odległość między parą sił

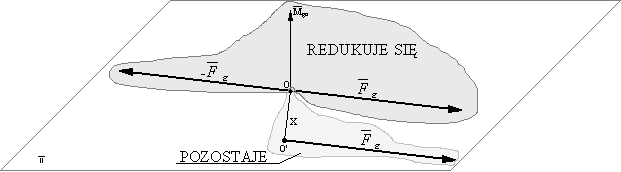
Do układu sił dodajemy parę sił. Siły
_g i -
_g równoważą się, redukuje się również moment główny, pozostaje tylko jedna siła ale przesunięta o x od bieguna.

17

Rys a)

---