WYKŁAD 1 30.09.2006
dr ZYGMUNTA BARAŃSKA
Literatura:
L. Hryniewicka „Ćw statystyczne w naukach ekonomicznych” ODDK, 2003
A. Komosa „Statystyka zbiór zadań”
PODSTAWOWE POJĘCIA
Statystyka:
Zestaw liczb zebranych i zinterpretowanych do przedstawienia określonego problemu
Wartości (parametry) wyliczane na podstawie badań próbnych
Nauka zajmująca się zbieraniem, prezentacją i analizą zebranego materiału (przeważnie liczbowego)
STATYSTYKA
Statystyka opisowa
proste przeliczenia arytmetyczne, nie wymagające znajomości rachunku prawdopodobieństwa; dotyczy sytuacji gdy badane są wszystkie występujące zdarzenia
Statystyka matematyczna
procedury oparte na matematyce, a w szczególności na rachunku prawdopodobieństwa, stosowana w sytuacji gdy badamy przedstawicieli określonej grupy biorącej udział w badaniu
Zbiorowość statystyczna - ogół osób lub rzeczy, które podlegają badaniu, składa się z jednostek statystycznych
Zjawiska masowe - służą do zauważenia prawidłowości statystycznych
ANALIZA ETAPÓW BADAŃ STATYSTYCZNYCH
I. PROGRAMOWANIE BADANIA
Określenie celu badania:
cele ogólne
cele szczególne (hipotezy szczegółowe)
Określenie przedmiotu badana - tj. określenie zbiorowości statystycznej i jednostki statystycznej; zbiorowość statystyczną określamy trzema stałymi cechami:
kto jest badany (cecha rzeczowa)
kiedy jest badany (cecha czasowa)
gdzie jest badany (cecha przestrzenna)
Zbiorowości:
statyczne - badane w pewnym momencie
dynamiczne - badane w pewnym okresie czasu
przeliczalne - zawierają konkretną liczbę jednostek
nieprzeliczalne - nie można określić liczby jednostek
jednorodne
niejednorodne - dzielimy na podzbiorowości jednorodne
Określenie zakresu badania (wyodrębnienie cech badanych u jednostek statystycznych)
Wybór zakresu obserwacji / wybór typu badania:
badanie całkowite (pełne) - do badania bierzemy wszystkie jednostki wchodzące w skład zbiorowości (np. spis ludności, spis gospodarstw rolnych, rejestracja urodzeń i zgonów, inwentaryzacja środków trwałych w przedsiębiorstwie)
badanie częściowe - badamy tylko część jednostek zbiorowości
▪ dobór jednostek w sposób losowy (każda jednostka ma znane prawdopodobieństwo wejścia do grupy badanej; stosowany odpowiedni schemat losowania)
▪ dobór jednostek w sposób nielosowy (przeprowadzający badanie sam decyduje kto bierze udział w badaniu)
badanie monograficzne - jedna wybrana jednostka zostaje opisana wszechstronnieOrganizacja obserwacji statystycznej:
jednorazowa
powtarzalna
ciągła
Wybór techniki zbierania danych
wywiad osobisty
samospisywanie (ankieta pocztowa)
bezpośrednia obserwacja lub pomiar
rejestry i dane sprawozdawcze
Gromadzenie danych statystycznychKontrola materiału statystycznego
ilościowa (kompletności)
merytoryczna (poprawnosci)
Ustalenie zasad klasyfikacji:
porządkowanie
grupowanie statystyczne:
wariancje - dla cech ilościowych wyodrębniamy warianty liczbowe
typologie - dla cech jakościowych wyodrebniamy grupy typologiczne
Budowa szeregów statystycznych - powstają w wyniku grupowania i porządkowania
szczegółowe (wyliczające)
rozdzielcze z cechą jakościową (strukturalne)
rozdzielcze z cechą ilościową (punktowe = jednostopniowe, przedziałowe = wielostopniowe)
kumulacyjne
geograficzne (przestrzenne)
czasowe (dynamiczne, chronologiczne)
stosowany dla cechy ciągłej lub dla cechy skokowej gdy jest duża liczba wariantów i duża liczba obserwacji
<xi0,xi1): xi0 - dolna granica przedziału czasowego; xi1 - górna granica przedziału czasowego
szeregi zamknięte: 15,0 - 25,0; 25,0 - 35,0...45,0 - 55,0
szeregi otwarte: poniżej 25,0; 25,0 - 35,0; ...; 45,0 - 55,0; powyżej 55,0
punktowe
liniowe
powierzchniowe (najczęściej dla szeregów rozdzielczych strukturalnych)
bryłowe
dla szeregu rozdzielczego jednopunktowego najczęściej słupkowy diagram odcinkowy
szeregi rozdzielcze przedziałowe - wykres liniowy, powierzchniowy
jeśli rozpiętości przedziałów klasowych są równe to:
szeregi czasowe na wykresach liniowych lub powierzchniowych
tablice proste
tablice złożone
tablice kombinowane
tablice specjalne
Tablica prosta - zawiera tylko jeden szereg
Tablica złożona - zawiera więcej niż jeden szereg
Tablica kombinowana - ma przeliczenia lub doliczenia, może mieć więcej niż jeden szereganaliza struktury
analiza korelacji
analiza szeregów dynamicznych i ich dekompozycja
wyliczanie miar tendencji centralnej
obliczanie miar dyspersji (rozproszenia)
obliczanie miar skośności (asymetrii)
obliczanie miar koncentracji
budujemy szereg
nanosimy dane na wykres - wykres może mieć różne rozkłady:
liczona z wszystkich wartości szeregu
∑ odchyleń każdego x od średniej daje wartość 0:
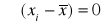
50% zbiorowości ma wartości cechy nie większe niż mediana
50% zbiorowości ma wartości cechy nie mniejsze niż mediana
25% zbiorowości ma wartości cechy nie większe niż Q1
75% zbiorowości ma wartości cechy nie mniejsze niż Q1
75% zbiorowości ma wartości cechy nie większe niż Q3
25% zbiorowości ma wartości cechy nie mniejsze niż Q3
10% zbiorowości ma wartości cechy nie większe niż D1
90% zbiorowości ma wartości cechy nie mniejsze niż D1
90% zbiorowości ma wartości cechy nie większe niż D9
10% zbiorowości ma wartości cechy nie mniejsze niż D9
szereg szczegółowy
szereg rozdzielczy jednostopniowy
aby wyliczyć Me należy zbudować szereg kumulowany (skumulować szereg): nsk
w szeregu skumulowanym szukamy pozycji mediany (pMe):
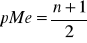
szereg rozdzielczy wielostopniowy
kumulujemy szereg
pozycja mediany (pMe):
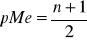
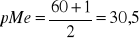
mediana:
szereg szczegółowy
szereg rozdzielczy jednostopniowy
szereg rozdzielczy wielostopniowy
szereg rozdzielczy jednostopniowy
kumulujemy szereg
pozycja Q1:
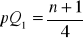
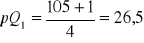
kwartyl Q1:
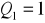
(czyli ten xi dla którego jest pQ1)szereg rozdzielczy wielostopniowy
kumulujemy szereg
pozycja Q1 (Q3)
Q1 (Q3)
Miary rozproszenia / dyspersji
miary klasyczne (bezwzględne, względne)
miary pozycyjne (bezwzględne, względne)
Wariancja s2 - bezwzględna
Odchylenie standardowe s - bezwzględna - mówi o przeciętnym odchyleniu poszczególnych wartości na „+” lub „-” od średniej
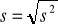
Współczynnik zmienności V(s) - względny - służy do porównywania szeregów,
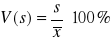
Rozstęp R - bezwzględny,
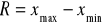
Odchylenie ćwiartkowe Q - bezwzględny,
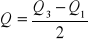
- dyspersja dla wartości pomiędzy ćwiartką 3 i 1; połowa obszaru pomiędzy ćwiartką 1 i 3; przeciętne odchylenie od mediany od Q1 do Q3.Współczynnik zmienności V(Q) - względny,
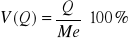
; dyspersja w % pomiędzy Q1 i Q3.Miary klasyczne
Miary pozycyjne
Miary mieszanemoment trzeci centralny
współczynnik asymetrii
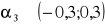
- asymetria niewielka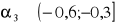

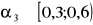
- asymetria umiarkowana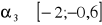

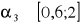
- asymetria wyraźna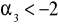

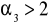
- mamy do czynienia ze zbiorowością niejednorodnąwspółczynnik asymetrii A(Q)
współczynnik asymetrii A(D)
współczynnik asymetrii
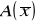
współczynnik asymetrii A(Me)
moment czwarty centralny
współczynnik skupienia
Moment centralny r-tego rzędu
Moment zwykły r-tego rzędu:
metoda graficzna: krzywa Lorentza
współczynnik koncentracji Pearsona
wielowymiarowy - nie omawiamy
dwuwymiarowy - omawiamy
funkcyjny [y = f(x)] - zawsze zapisywany w postaci funkcji jednej zmiennej (konkretnej wartości jednej zmiennej odpowiada konkretna wartość drugiej zmiennej)
stochastyczny - jednej wartości y może odpowiadać szereg wartości x [y = f(x1, x2, x3)]
korelacyjny - jednej wartości y odpowiada wartość średnia x [
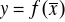
]jednostronne
dwustronne
współczynniki korelacji
analiza regresji
Wyliczenie współczynników, które mówią o kierunku i sile zależności między dwoma cechami
pierwsza 2 powinna mieć nr 2
druga 2 powinna mieć nr 3
więc: 2+3=5
5:2(bo były dwie 2)=2,5 → każda dwójka będzie miała nr 2,5pierwsza 3 powinna mieć nr 4
druga 3 powinna mieć nr 5
trzecia 3 powinna mieć nr 6
więc 4+5+6=15
15:3(bo były trzy 3)=5 → każda trójka będzie miała nr 5x rośnie i y rośnie - korelacja prostoliniowa dodatnia
x rośnie y maleje - korelacja prostoliniowa ujemna
x rośnie y nie wykazuje wyraźnych zmian - korelacji brak
korelacja prostoliniowa ujemna ale słabsza niż w przypadku b) - im większy rozrzut pkt-ów tym słabsza korelacja
korelacja prostoliniowa dodatnia - słabsza niż w przypadku a)
korelacja prostoliniowa ujemna - silniejsza niż w d) słabsza niż w b)
korelacja prostoliniowa dodatnia - bardzo słaba
korelacja krzywoliniowa
Każda jednostka statystyczna różni się od pozostałych pewnymi właściwościami cech (poziomem cech)
CECHY ZMIENNE
Ilościowe
można przedstawić w formie liczb, mierzalne
Jakościowe
właściwości, które można określić tylko słownie
Skokowa
z pewnego przedziału liczbowego przyjmuje tylko określone wartości liczbowe; np. {2,4,5,7,8}
Ciągła
z pewnego przedziału liczbowego może przyjmować dowolną liczbę wartości; np. (2,8)
Dwudzielna
może przyjmować tylko dwie kategorie; np. płeć = kobieta lub mężczyzna
Wielodzielna
może przyjmować więcej niż dwie kategorie; np. ukończona szkoła średnia = liceum lub technikum lub zawodówka, it
II. OBSERWACJA STATYSTYCZNA
Materiał pierwotny
zebrany ściśle do celów badania
Materiał wtórny
zebrany do innych celów, a wykorzystywany m.in. do danego badania
III. OPRACOWANIE DANYCH
Szereg statystyczny - ciąg wartości licznowych i nieliczbowych badanej cechy uporządkowany wg określonych kryteriów
Rodzaje szeregów statystycznych:
♦ szereg rozdzielczy strukturalny
poziom wykształcenia |
liczba osób |
podstawowe zasadnicze zawodowe średnie ... |
6 26 19 ... |
♦ szereg rozdzielczy punktowy
liczba dzieci na utrzymaniu xi |
liczba osób ni |
0 1 ... |
34 26 ... |
♦ szereg rozdzielczy jednopunktowy (np. odziały banku wg ilości stanowisk)
ilość stanowisk |
ilość oddziałów |
... ... |
... ... |
♦ szereg rozdzielczy przedziałowy
wiek w latach <xi0,xi1) |
liczba osób ni |
15,0 - 25,0 25,0 - 35,0 ... |
14 32 ... |
♦ szereg geograficzny
województwo |
przeciętne miesięczne wynagrodzenie |
... ... ... |
... ... ... |
♦ szereg dynamiczny
grupy wiekowe |
ludność w tyś. |
||
|
1970 |
1980 |
1990 |
przedprodukcyjny produkcyjny ... |
x a ... |
y b ... |
z c ... |
♦ szereg szczegółowy - szereg tylko uporządkowany, nie pogrupowany = szereg prosty
SYMBOLE
R - obszar zmienności / rozstęp
![]()
n - liczebność / ogólna liczba obserwacji
k - ilość przedziałów klasowych
![]()
c - rozpiętość przedziału klasowego
![]()
IV. PREZENTACJA GRAFICZNA - zbudowanie wykresu statystycznego dla kolejnych szeregów statystycznych.
Rodzaje wykresów:
♦ dla wykresy powierzchniowego - histogram:
na osi ox granice przedziałów
na osi oy liczba obserwacji
♦ dla wykresu liniowego
na osi ox środki przedziałów klasowych (![]()
)
![]()
na osi oy liczba obserwacji
na osi ox lata
na osi oy badana cecha
WYKŁAD 2 01.10.2006
Tablica statystyczna - przedstawienie jednego lub więcej szeregów jednocześnie; część liczbowa tablicy składa się z odpowiednich kolumn i wierszy a część opisowa z tytułu (określenie zbiorowości) i wierszy (boczek tablicy); każdy wiersz tablicy musi być wypełniony nazwą kolumn (główka tablicy); pod każdą tablicą musi być podane źródło danych; pod tablicą mogą być zamieszczone informacje dodatkowe.
W tablicach używa się następujących znaków umownych:
kropka (∙) - oznacza zupełny brak wiarygodnych informacji
zero (0) - oznacza, że dane zjawisko występuje ale w ilościach mniejszych niż pół jednostki miary przyjętej w tablicy
kreska (-) - oznacza, że dane zjawisko nie występuje
gwiazdka (*) - stawiana jest obok liczby, która została zmieniona w stosunku do poprzednio opublikowanej
napis „w tym” - oznacza, że nie podaje się wszystkich składników sumy ogólnej
iks (x) - oznacza, że rubryki nie można wypełnić ze względu na układ tablicy
Rodzaje tablic:
makroregion |
współczynnik aktywności zawodowej |
Stołeczny Północny ... |
58,6 56,4 ... |
|
ludność w tyś |
||
|
1970 |
1980 |
1990 |
przedprodukcyjny produkcyjny ... |
a b ... |
c d ... |
e f ... |
grupy wiekowe |
razem |
M |
K |
przedprodukcyjny produkcyjny ... |
5 3 ... |
2 1 ... |
3 2 ... |
ANALIZA STATYSTYCZNA
Analiza statystyczna - wyliczenie pewnych parametrów na podstawie zbudowanych szeregów w celu określenia pewnych prawidłowości w badanej zbiorowości
Analizę statystyczną rozpatrujemy wg pojęć:
I. ANALIZA STRUKTURY
Analiza struktury dla cech ilościowych:
1. Miary tendencji centralnej = miary położenia
miary klasyczne
jest to średnia arytmetyczna; liczone są dla szeregów rozdzielczych o zamkniętych przedziałach klasowych; nie liczymy dla szeregów skrajnie asymetrycznych, bimodalnych, u-towych;
miary pozycyjne
liczymy tylko z określonych wartości szeregu; należą do nich: mediana (Me), dominanta (D), kwartyle: pierwszy (Q1), trzeci (Q3), decyle: pierwszy (D1), dziewiąty (D9)
Właściwości średniej arytmetycznej (= wartości przeciętnej)
Me (mediana) - wartość środkowa badanej cechy (szeregu), dzieli szereg w ten sposób, że:
D (dominanta) - wartość w szeregu występująca najliczniej
Q1, Q3 (kwartyle) - dzielą zbiorowość na cztery części
Q1 - dzieli szereg w ten sposób, że:
Q3 - dzieli szereg w ten sposób, że:
D1, D9 (decyle) - dzielą zbiorowość na dziesięć części
D1 - dzieli szereg w ten sposób, że:
D9 - dzieli szereg w ten sposób, że:
Zależność pomiędzy D, D1, D9, Q1, Q3, Me, ![]()
:
Aby liczyć miary pozycyjne szereg musi być liczny
MEDIANA Me
5, 5, 6, 6, 7, 7, 8, 9, 10
Me = 7 (bo 7 leży po środku szeregu)
5, 5, 6, 6, 7, 7, 8, 9 ![]()
![]()
xi |
ni |
nsk |
5 |
2 |
2 |
6 |
2 |
4 (=2+2) |
7 |
2 |
6 (=4+2) |
8 |
1 |
7 (=6+1) |
9 |
1 |
8 (=7+1) |
10 |
1 |
9 (=8+1) |
xi - wydajność
ni - ilość pomiarów
![]()
(piąta obserwacja w szeregu jest medianą, szukamy obserwacji równej lub pierwszej większej); czyli ![]()
xi |
ni |
nsk |
0-2 |
10 |
10 |
2-4 |
20 |
30 (=10+20) |
4-6 |
10 |
40 (=30+10) |
6-8 |
10 |
50 (=40+10) |
8-10 |
10 |
60 (=50+10) |
![]()
, gdzie: ci - rozpiętość przedziału mediany,
ni - liczebność w przedziale mediany
![]()
![]()
; ![]()
; ![]()
; ![]()
![]()
![]()
Środkowa wartość cechy wynosi 4,1
DOMINANTA D
5, 5, 6, 6, 7, 7, 8, 9, 10
W tym szeregu dominanty brak (bo żadna wartość pomiaru nie występuje częściej niż inna)
5, 5, 6, 6, 7, 7, 7, 8, 9, 10
D = 7 (bo 7 występuje najczęściej)
xi |
ni |
5 |
2 |
6 |
2 |
7 |
3 |
8 |
1 |
9 |
1 |
10 |
1 |
D = 7 (bo 7 występuje najczęściej)
xi |
ni |
0-2 |
10 |
2-4 |
20 |
4-6 |
10 |
6-8 |
10 |
8-10 |
10 |
![]()
![]()
![]()
Aby można było policzyć dominantę to przedział dominanty, przedział ją poprzedzający i następujący po niej muszą mieć tą samą rozpiętość: ![]()
KWARTYLE Q1, Q3
xi |
ni |
nsk |
0 |
20 |
20 |
1 |
50 |
70 (=50+20) |
2 |
20 |
90 (=70+20) |
3 |
10 |
100 (=90+10) |
4 |
5 |
105 (=100+5) |
Q3 - analogicznie jak Q1:
![]()
![]()
![]()
xi |
ni |
nsk |
10-20 |
20 |
20 |
20-30 |
50 |
70 |
30-50 |
20 |
90 |
50-70 |
10 |
10 |
70-100 |
10 |
110 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
DECYLE D1, D9
Liczymy analogicznie jak kwartyle, gdzie:
![]()
![]()
![]()
![]()
Dyspersja - rozproszenie (odległość) poszczególnych wartości od średniej (![]()
); dzielimy ją na:
MIARY KLASYCZNE DYSPERSJI:
MIARY POZYCYJNE DYSPERSJI:
Dyspersja: do 10% - małe zróżnicowanie zbiorowości
10% do 35% - przeciętne zróżnicowanie
35%< - duże zróżnicowanie
WYKŁAD 3 21.10.2006
W rozkładach symetrycznych odchylenie ćwiartkowe wynosi ![]()
odchylenia standardowego:![]()
.
Jeśli mamy wybór to lepsze są metody klasyczne - obejmują cały szereg.
3. Miary asymetrii - skośności
Asymetria = skośność - nierównomierne rozłożenie liczebności wokół średniej:
Rozkłady symetryczne - 50% jednostek leży poniżej i 50% jednostek leży powyżej średniej
Asymetria prawostronna (dodatnia) - ponad 50% obserwacji ma wartości poniżej średniej (![]()
); lub inaczej: dominująca grupa obserwacji ma wartości poniżej średniej
Asymetria lewostronna (ujemna) - ponad 50% obserwacji leży powyżej średniej (![]()
); lub inaczej: dominująca grupa obserwacji ma wartości powyżej średniej
MIARY KLASYCZNE
![]()
jeśli: ![]()
to mówimy, że rozkład jest symetryczny![]()
- asymetria lewostronna![]()
- asymetria prawostronna
Moment trzeci centralny liczymy gdy można policzyć średnią arytmetyczną
![]()
, ![]()
mówi o sile asymetrii:
![]()
- rozkład symetryczny![]()
- asymetria lewostronna![]()
- asymetria prawostronna
MIARY POZYCYJNE
![]()
gdzie ![]()
dla: ![]()
- rozkład symetryczny![]()
- asymetria prawostronna![]()
- asymetria lewostronna![]()
![]()
![]()
- mamy do czynienia ze zbiorowością niejednorodną
Jest to asymetria dla obszaru od![]()
do ![]()
, NIE obejmuje wszystkich wartości szeregu
Współczynnik asymetrii A(Q) liczymy gdy nie można policzyć średniej arytmetycznej
![]()
gdzie ![]()
Liczony jeśli nie można wyliczyć![]()
, mówi o asymetrii w obszarze od![]()
do![]()
MIARY MIESZANE
![]()
gdzie ![]()
Aby go policzyć, musi być możliwość policzenia D, interpretacja jak wyżej (przy A(Q))
![]()
gdzie ![]()
Liczony jeśli nie można wyliczyć D
4. Miary skupienia - kurtozy
Skupienie (kurtoza) - rozpatrywanie jak leżą określone wartości wokół średniej skupienie wartości wokół średniej)
Liczymy tyko gdy rozkłady są symetryczne, lub zbliżone do symetrycznych:
Rozkład normalny - jest rozkładem teoretycznym; pierwszym pkt-em przegięcia jest odchylenie standardowe
Badamy na ile dane skupienie jest większe/mniejsze od rozkładu normalnego
![]()
NIE INTERPRETUJEMY
![]()
jeśli:
![]()
rozkład o spłaszczeniu takim jak rozkład normalny![]()
rozkład wysmukły![]()
rozkład spłaszczony
Skupienie -3 = ekses (![]()
) spotykane w literaturze
W statystyce istnieją moment centralne (![]()
) i momenty zwykłe (m)
![]()
![]()
Koncentracja
Koncentracja - nie równomierny podział rozpatrywanej cechy
Omawiamy na przykładzie:
Miarą koncentracji jest
Rozkład wynagrodzeń w sektorze edukacji (99r)
|
wysokość trapezu |
oś x na diagramie |
|
|
|
oś y na diagramie (podstawy kolejnych trapezów) |
suma podstaw poszczególnych trapezów dzielona na 2 |
pola poszczególnych trapezów (niw% = wysokość trapezu) |
|
|
|
|
|
|
( |
|
|
300-540 |
5,3 |
5,3 |
420 |
2226 |
2,3 |
2,3 |
1,15 |
6,1 |
540-700 |
18 |
23,3 |
620 |
11160 |
11,4 |
13,7 |
8 |
144 |
700-780 |
9,1 |
32,4 |
740 |
6784 |
6,9 |
20,6 |
17,5 |
156,07 |
780-860 |
10,3 |
42,7 |
820 |
8446 |
8,6 |
29,2 |
24,9 |
256,47 |
860-940 |
10,8 |
53,5 |
900 |
9720 |
9,9 |
39,1 |
34,2 |
369,36 |
940-1020 |
10,2 |
63,7 |
980 |
9996 |
10,2 |
49,3 |
44,2 |
450,84 |
1020-1200 |
16,7 |
80,4 |
1110 |
18537 |
18,9 |
68,2 |
58,8 |
981,96 |
1200-1500 |
13,5 |
93,9 |
1350 |
18255 |
18,6 |
86,8 |
77,5 |
1046,25 |
1500-2000 |
4,3 |
98,2 |
1750 |
7525 |
7,7 |
94,5 |
90,7 |
390,01 |
2000-4000 |
1,8 |
100 |
3000 |
5400 |
5,5 |
100 |
97,3 |
175,14 |
|
100 |
|
|
97969 |
|
|
|
Pole b = 3976,06 |
![]()
=(![]()
w%)sk
Koncentracja będzie mała gdyż krzywa koncentracji leży blisko linii równomiernego rozkładu
WSPÓŁCZYNNIK KONCENTRACJI PEARSONA:
![]()
gdzie ![]()
Aby obliczyć K musimy znać wartość pola a i pola b:
![]()
(pole trójkąta leżącego pod linią równomiernego rozkładu)
stąd: ![]()
otrzymujemy:![]()
Ponieważ nie znamy f-cji opisującej krzywą koncentracji musimy w przybliżeniu obliczyć pole b. Po zrzutowaniu wszystkich pkt-ów na oś ox i założeniu że odległości pomiędzy kolejnymi pkt-ami na krzywej koncentracji są mierzone po linii prostej otrzymujemy pole b jako sumę pól trapezów
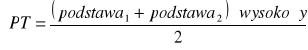
Otrzymujemy b = 3976,06 więc:![]()
INTERPRETACJA:
K = 0,2 - mała koncentracja, mały odsetek osób ma 20% ogółu wynagrodzeń, zaś duża liczba pozostałych ma ok. 80% wszystkich wynagrodzeń.
METODY ANALIZY CECH JAKOŚCIOWYCH
Wskaźnik struktury (frakcja, częstość względna)
![]()
, ![]()
- udział procentowy
Dla cech jakościowej można policzyć tylko wi.
Względny wskaźnik podobieństwa struktur:
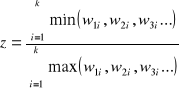
gdzie ![]()
jeśli: ![]()
- struktury są identyczne![]()
- struktury są zupełnie różne![]()
- struktury średnio podobne
Wskaźnik natężenia
![]()
lub ![]()
lub ![]()
WYKŁAD 4 28.10.2006
W analizie struktury rozpatrujemy 4 obszary:
1. rozstęp: ![]()
2. typowy obszar zmienności ![]()
, ![]()
3. rozstęp kwartylowy ![]()
4. rozstęp decylowy ![]()
Graficzne wyznaczanie dominanty (D), mediany (Me), kwartyli (![]()
, ![]()
) i decyli (![]()
, ![]()
)
|
|
|
0-2 |
10 |
10 |
2-4 |
20 |
30 |
4-6 |
30 |
60 |
6-8 |
10 |
70 |
8-10 |
10 |
80 |
Dominanta - wyznaczamy za pomocą histogramu
Mediana - wyznaczamy przy pomocy krzywej kumulacyjnej
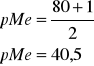
Analogicznie wyznaczamy kwartyle - szukając pozycji Q1 i Q3 oraz decyle - szukając pozycji D1 i D9
KORELACJA = związek cech
Związki dwuwymiarowe dla cech ilościowych:
staż pracy |
wydajność w sztukach |
2 |
2 |
2 |
3 |
2 |
1 |
METODY ANALIZY ZWIĄZKÓW KORELACYJNYCH
CECHY ILOŚCIOWE → WSPÓŁCZYNNIK KORELACJI r - PEARSONA
współczynnik korelacji Pearsona (r) - można go stosować tylko jeśli rozrzut pkt-ów jest liniowy
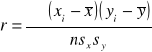
dla ![]()
gdzie: n - liczba par obserwacji
sx - odchylenie standardowe dla x
sy - odchylenie standardowe dla y
![]()
co najmniej 100 obserwacji
INTERPRETACJA:
![]()
- korelacja bardzo słaba (mało znacząca dla mniej niż 100 obserwacji)
![]()
- korelacja niska, mała
![]()
- korelacja umiarkowana
![]()
- korelacja znaczna, wyraźna
![]()
- korelacja wysoka, pewna
![]()
- korelacja przechodzi w związek funkcyjny
PRZYKŁAD
wiek |
cena auta |
|
|||||||
|
|
|
|
|
|
|
|
|
|
1 |
40 |
1 |
1600 |
40 |
36,13 |
3,87 |
14,96 |
15,44 |
283,39 |
2 |
32 |
4 |
1024 |
64 |
31,96 |
0,04 |
0,00 |
7,44 |
55,35 |
2 |
33 |
4 |
1089 |
66 |
31,96 |
1,04 |
1,07 |
8,44 |
71,23 |
3 |
27 |
9 |
729 |
81 |
27,80 |
-0,80 |
0,63 |
2,44 |
5,95 |
3 |
25 |
9 |
625 |
75 |
27,80 |
-2,80 |
7,82 |
0,44 |
0,19 |
3 |
26 |
9 |
676 |
78 |
27,80 |
-1,80 |
3,23 |
1,44 |
2,07 |
5 |
17 |
25 |
289 |
85 |
19,46 |
-2,46 |
6,05 |
-7,56 |
57,15 |
7 |
12 |
49 |
144 |
84 |
11,12 |
0,88 |
0,77 |
-12,56 |
157,75 |
8 |
9 |
64 |
81 |
72 |
6,96 |
2,04 |
4,18 |
-15,56 |
242,11 |
34 |
221 |
174 |
6257 |
645 |
221 |
X |
38,71 |
X |
830,22 |
y - cecha zależna (cena auta zależy od wieku auta)
x - cecha niezależna (wiek auta nie zależy od jego ceny)
r - można też liczyć ze wzoru:
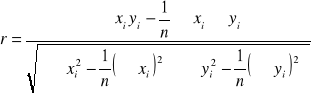
→ ![]()
- korelacja wysoka
SKALA PORZADKOWA → WSPÓŁCZYNNIK KORELACJI rs - SPEARMANA
wiek |
cena auta |
|
|
|
|
|
|
|
|
1 |
40 |
1 |
9 |
64 |
2 |
32 |
2,5 |
7 |
20,25 |
2 |
33 |
2,5 |
8 |
30,25 |
3 |
27 |
5 |
6 |
1 |
3 |
25 |
5 |
4 |
1 |
3 |
26 |
5 |
5 |
0 |
5 |
17 |
7 |
3 |
16 |
7 |
12 |
8 |
2 |
36 |
8 |
9 |
9 |
1 |
64 |
34 |
221 |
X |
X |
232,5 |
NADAWANIE NR RANGOWYCH:
Nadajemy wartościom x i y nr zgodnie z przyjętym porządkiem (rosnącym - u nas, lub mającym). Najmniejsza wartość x będzie miała nr 1, druga w kolejności nr 2, trzecia w kolejności nr 3, itd. Jeśli jednak jest więcej niż jeden identyczny x to nr tworzymy następująco:
W ten sposób powstają rangi wiązane.
Z y postępujemy analogicznie: y=9 jest najmniejszy więc ma nr 1, a y=40 jest największy więc ma nr 9
współczynnik Spearmana (mniej dokładny niż współczynnik Pearsona):
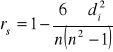
, gdzie n - liczba par obserwacji
rs = -0,94 → interpretacja taka sama jak przy wsp. Pearsona
Jeśli ponad 25% jest rang wiązanych to liczymy współczynnik Spearmena z poprawką na rangi wiązane:
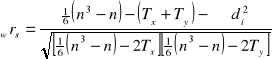
przy czym: ![]()
gdzie: Tx poprawka na rangi wiązane x;
Ty - poprawka na rangi wiązane y;
t - ilość wspólnych wiązań
PRZYKŁAD
x |
y |
rangi x |
rangi y |
|
|
36 27 40 19 26 35 37 28 27 26 46 34 40 34 23 38 20 24 12 |
27 25 39 17 21 22 29 17 17 18 39 21 27 29 15 38 21 19 10 |
6 11,5 2,5 18 13,5 7 5 10 11,5 13,5 1 8,5 2,5 8,5 16 4 17 15 19 |
6,5 8 1,5 16 11 9 4,5 16 16 14 1,5 11 6,5 4,5 18 3 11 13 19 |
-0,5 3,5 1 2 2,5 -2 0,5 -0,6 -4,5 -0,5 -0,5 -2,5 4 4 -2 1 6 2 0 |
0,25 12,25 1 4 6,25 4 0,25 36 20,25 0,25 0,25 6,25 16 16 4 1 36 4 0 |
X |
X |
X |
X |
0 |
168 |
Rangi wiązane x |
2,5 |
8,5 |
11,5 |
13,5 |
|
ti |
2 |
2 |
2 |
2 |
|
|
6 |
6 |
6 |
6 |
|
![]()
Rangi wiązane y |
1,5 |
4,5 |
6,5 |
11 |
16 |
|
ti |
2 |
2 |
2 |
3 |
3 |
|
|
6 |
6 |
6 |
24 |
24 |
|
![]()
CECHY JAKOŚCIOWE → WSPÓŁCZYNNIK Q - KENDALLA; T - CZUPROWA; C - PEARSONA
Dane muszą być przedstawione w formie tablicy.
PRZYKŁAD:
Czy płeć determinuje posiadanie karty bankomatowej?
karta bankomatowa |
płeć |
|
|||
|
K |
M |
|
||
posiada |
20 |
a |
90 |
b |
110 |
nie posiada |
110 |
c |
30 |
d |
140 |
|
130 |
120 |
250 |
||
Jeśli obie cechy są dwudzielne to tablica nazywa się dwa na dwa - przyjmujemy wtedy współczynnik asocjacji (Kendalla) Q:
![]()
dla ![]()
INTERPRETACJA: ![]()
- słabe / umiarkowane powiązanie
![]()
- wyraźne powiązanie
![]()
- silne powiązanie
![]()
- mamy wyraźną zależności płci i posiadania karty bankomatowej, karty posiadają gł. mężczyźni
współczynnik asocjacji jest najmniej dokładny, lepiej liczyć
współczynnik kontyngencji (Pearsona ) C:
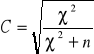
dla ![]()
- jest najdokładniejszy
lub
współczynnik Czuprowa T
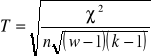
dla ![]()
gdzie: n - liczba obserwacji
w - liczba wierszy tablicy
k - liczba kolumn tablicy
![]()
Statystyka dla tablicy 2×2 i n>40:
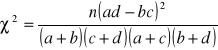
→ ![]()
Otrzymujemy: T = 0,6 i C = 0,51 → zależność umiarkowana
21
STATYSTYKA WYKŁADY
Utworzony przez Ania Marzec
1 szereg
2 szereg
Symetria normalna
Symetria spłaszczona
Symetria wysmukła
Asymetria zdecydowana lewostronna (ujemna)
Asymetria skrajna lewostronna (ujemna)
Asymetria umiarkowana lewostronna (ujemna)
Asymetria zdecydowana prawostronna (dodatnia)
Asymetria skrajna prawostronna (dodatnia)
Asymetria umiarkowana prawostronna (dodatnia)
Rozkład u-towy (siodłowy)
Rozkład równomierny
Rozkład bimodalny
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
D
Me
Rozkład wielomodalny
Rozkład jednopunktowy
D Me ![]()
![]()
Rozkład dwupunktowy (dla cechy dwudzielnej)
10%
![]()
Me D
100%
10%
![]()
100%
krzywa koncentracji
a
b
linia równomiernego rozkładu = brak koncentracji
![]()
w%
(![]()
w%)sk
Im dalej od przekątnej leży krzywa koncentracji tym większa koncentracja
III
II
I
![]()
![]()
D
Me
D Me ![]()
![]()
![]()
Me D
![]()
asymetria lewostronna (ujemna)
asymetria prawostronna (dodatnia)
rozkład symetryczny
I rozkład spłaszczony = platokurtyczny
II rozkład wysmukły = leptokurtyczny
III rozkład spłaszczony jak rozkład normalny
30
![]()
s
-s
p.p.
p.p.
20
10
10
8
6
4
2
xi
ni
D
Me
ni
xi
2
4
6
8
10
10
20
30
70
60
40,5
80
k = 2
(dwie cechy)
skale pomiarowe
obie cechy są jakościowe
skale nominalne
cechy ilościowe i jakościowe wyrangowane
skale porządkowe
obie cechy są ilościowe
skala interwałowa i ilorazowa
cecha jakościowa i ilościowa
współczynniki korelacji
T - Czuprowa
Q - Kendalla (asocjacji)
C - Pearsona (kontyngencji)
są jeszcze 2 - nie zajmujemy się nimi
rs - Spearmana
są jeszcze 2 - nie zajmujemy się nimi
r - Pearsona
jest jeszcze 1 - nie zajmujemy się nim
są 2 Pearsona nie zajmujemy się nimi
h)
g)
f)
e)
d)
c)
b)
a)
r=-0,9
r=0,6
r=0,4
r=-0,8
40
![]()
- nr rangowy x
![]()
- nr rangowy y
![]()
- różnica w rangach x i y
r=1
r=-1
korelacja liniowa ujemna
6
7
8
ni
xi
1
3
2
4
5
10
20
30
r=0
Wyszukiwarka