Aparatura
Do wykonania tego ćwiczenia niezbędne były: generator, opornik, woltomierz, kondensator, cewka indukcyjna, przewody.
Schemat doświadczenia:
Połączyliśmy układ jak na rysunku :
Szeregowy
Równoległy
Pomiary:
Doświadczenie przeprowadziliśmy w kilku etapach. Na początku połączyliśmy obwód szeregowo po czym zaczęliśmy zadawać odpowiednią częstotliwość na generatorze, która wynosiła od 22 do 100 Hz. Odczytywaliśmy zmiany napięć wskazywane przez woltomierz .Kolejnym krokiem było połączenie obwodu równolegle po czym zadawana częstotliwość na generatorze wynosiła od 50 do 100 Hz. Zapisywaliśmy zmiany napięć wskazywane przez woltomierz. Na podstawie naszych pomiarów mogliśmy określić częstotliwość rezonansową f jak i korzystając ze wzoru Thomsona znależć indukcyjność cewki L i niepewność U(L).
Obwód szeregowy
Częstotliwość zadana |
Zmiany napięcia |
50 |
7,76 |
51 |
7,70 |
52 |
7,64 |
53 |
7,58 |
54 |
7,52 |
55 |
7,48 |
56 |
7,44 |
57 |
7,41 |
58 |
7,38 |
59 |
7,36 |
60 |
7,35 |
62 |
7,32 |
64 |
7,32 |
66 |
7,33 |
68 |
7,36 |
70 |
7,40 |
72 |
7,46 |
74 |
7,53 |
76 |
7,60 |
Test Chi2
Z programu komputerowego „Matex” odczytaliśmy wartość liczby chi2 , która wynosi:
![]()
Porównaliśmy naszą liczbę z tabelą chi2 i w naszym przypadku poziom istotności α wynosi:
α= 0.9
Ze wzoru 1- α obliczyliśmy poziom ufności dopasowania:
α= 0,1
Im poziom ufności dopasowania jest bliższy zeru tym lepiej.
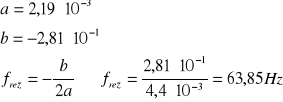
Obliczam niepewność U(f) z prawa propagacji :

Obwód równoległy
Częstotliwość zadana |
Zmiany napięcia |
55 |
11,16 |
56 |
11,20 |
57 |
11,21 |
58 |
11,25 |
59 |
11,28 |
60 |
11,29 |
62 |
11,32 |
64 |
11,36 |
66 |
11,37 |
68 |
11,38 |
70 |
11,39 |
72 |
11,39 |
74 |
11,38 |
76 |
11,36 |
78 |
11,34 |
80 |
11,31 |
82 |
11,28 |
84 |
11,23 |
86 |
11,17 |
88 |
11,11 |
90 |
11,04 |
Test Chi2
Z programu komputerowego „Matex” odczytaliśmy wartość liczby chi2 , która wynosi:
![]()
Porównaliśmy naszą liczbę z tabelą chi2 i w naszym przypadku poziom istotności α wynosi:
α= 0.99
Ze wzoru 1- α obliczyliśmy poziom ufności dopasowania:
1-α= 0,1
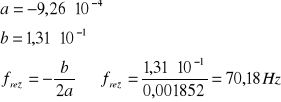
Obliczam niepewność U(f) z prawa propagacji :
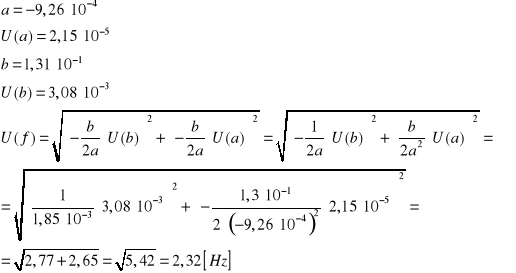
Obliczam indukcyjność cewki L :
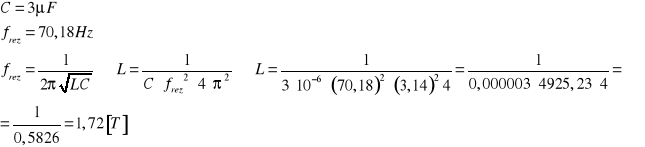
Niepewność wartości indukcyjności wyliczam ze wzoru :
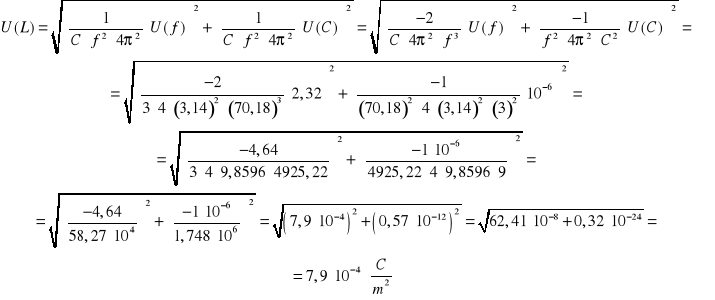
Drgania
Drgania - procesy, w trakcie których wielkości fizyczne na przemian rosną i maleją w czasie.
W zależności od drgającego medium wyróżniamy drgania mechaniczne, elektryczne, elektromechaniczne. Szczególnymi rodzajami drgań rozpatrywanymi w fizyce są:
drgania mechaniczne: wahadło matematyczne, ciało na sprężynie, wahadło fizyczne, drgania cząsteczek sieci krystalicznych, drgania strun instrumentów muzycznych, drgania powietrza.
drgania elektryczne: zmiany natężenia prądu w układzie kondensatora i cewki
drgania elektromechaniczne: drgania krystalicznych sieci jonowych.
Bez względu na drgajacą wielkość stosuje się podział ruchu drgającego ze względu na własności matematyczne funkcji opisującej drgania lub co jest równoważne na równania opisujące zachowanie się układu drgajacego. Wyróżnia się drgania okresowe i nieokresowe. Wśród drgań okresowych wyróżnia się często spotykany i najprostszy w opisie matematycznym ruch harmoniczny, a w drganiach nieokresowych drgania prawie okresowe.
W zależności od rodzaju równań drgań wyróżnia się drgania liniowe i drgania nieliniowe.
Jeżeli na drgajacy układ ma wpływ inny drgajacy układ to drgania nazywamy wymuszonymi. Układy autonomiczne (nie wymuszone) dzieli się na zachowawcze (energia drgań nie zmienia się), tłumione (energia zmniejsza się), samowzbudne (energia drgań rośnie).
Szczególnym przypadkiem drgań są drgania harmoniczne. Takie drgania powstają, gdy siła sprowadzająca układ drgający do położenia równowagi jest proporcjonalna do wychylenia układu z tego położenia.
Drgania harmoniczne
Szczególnym rodzajem drgań są drgania harmoniczne, tj. okresowe, o stałej amplitudzie, opisane sinusoidą. Ze względu na prostotę opisu drgania harmoniczne są wykorzystywane do opisu wielu drgań rzeczywistych jako ich przybliżenie (lub poprzez rozkład na nie).
Najprostsze równanie opisujące drgania harmoniczne (dla ciężarka zawieszonego na sprężynie) ma postać:
mx'' (t) + k x(t) = 0.
Rozwiązaniem jest funkcja
x(t)=Asinωt+φ0,
gdzie A - amplituda drgań
ω - częstość kołowa (ν - częstość drgań)
k - współczynnik sprężystości
m - masa ciała
φ0 - faza początkowa.
Ze względu na fizykę procesów wyróżnia się drgania mechaniczne i elektryczne.
Z reguły w życiu nie mamy do czynienia z jednym prostym harmonicznym ruchem drgającym. Można zauważyć że, w czasie wykonywania pomiaru przyspieszenie przy pomocy wahadła nie porusza się w niezmiennej płaszczyźnie. Poniżej znajduje się przypadek gdy mamy do czynienia ze złożeniem dwóch liniowych prostych ruchów harmonicznych.
Ruchy te są do siebie położone pod kątem prostym. Czyli płaszczyzny ich drgań są prostopadłe. Powstały ruch jest złożeniem dwóch niezależnych drgań o równaniach:
x = Ax cos(x t + δ )
y = Ay cos(y t + )
Rezonans
Rezonans - efekt fizyczny dotyczący ciał i cząstek drgających pod wpływem siły harmonicznej tłumionej.
Szybkość strat energii w tłumieniu b, masa m ciała i współczynnik sprężystości k siły harmonicznej określają częstotliwość drgań własnych ciała f0, które jednakże zanikają pod wpływem tłumienia. Jeżeli na to ciało działa jeszcze trzecia siła, oscylująca w czasie z częstotliwością f, to ciało drgające czerpie stąd energię, która jest wytracana w tłumieniu. Dochodzi do pewnego stanu stacjonarnego, w którym omawiane ciało drga z częstotliwością równą f.
Amplituda tych drgań zależy od częstotliwości f. Jeżeli f jest bliskie f0, to amplituda osiąga maksimum. Mówimy wtedy, że zachodzi rezonans amplitudy. Podobnie możemy mówić o rezonansie mocy, gdy energia pobierana przez ciało, a dostarczana przez oscylującą siłę zewnętrzną, osiąga maksimum dla pewnej częstości f bliskiej f0.
Drgania elektromagnetyczne
Obwód LC bez źródła prądu przemiennego.
Podobnie jak w poprzednim obwodzie płynie tu malejący prąd związany z rozładowywaniem się kondensatora. Malejący prąd, który płynie przez zwojnicę powoduje powstanie w niej zjawiska samoindukcji. W zwojnicy wytwarza się siła elektromotoryczna, która powoduje, że pomimo rozładowywania się kondensatora, prąd dalej płynie i powoduje ponowne ładowanie kondensatora.
|
Okres drgań elektromagnetycznych wynosi:
Wzory na wielkości w drganiach elektromagnetycznych są bardzo podobne do wzorów w drganiach mechanicznych. Wystarczy tylko odpowiednio zamienić wielkości.
Drgania mechaniczne |
|
Drgania elektromagnetyczne |
x (wychylenie) |
odpowiada |
Q (ładunek) |
A (amplituda) |
odpowiada |
|
V (prędkość) |
odpowiada |
I (natężenie) |
a (przyspieszenie) |
odpowiada |
|
m (masa) |
odpowiada |
L (indukcyjność) |
k (współczynnik proporcjonalności) |
odpowiada |
|
Waga statystyczna. Średnia ważona.
Załóżmy, że wykonano pomiary tej samej wielkości x za pomocą różnych przyrządów lub metod pomiarowych. Wyniki pomiarów są scharakteryzowane w każdej grupie wartością średnią ![]()
i niepewnością standardową ![]()
. Wartość średnia ważona wielkości x zdefiniowana jest następująco :
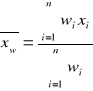
gdzie waga ![]()
pomiarów i- tej grupy jest obliczana ze wzoru :
![]()
a niepewność średniej ważonej jest średnią ważoną niepewności poszczególnych pomiarów :
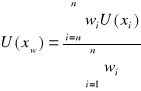
Wyszukiwarka