METODY BADANIA PIONOWOŚCI BUDOWLI WYSMUKŁYCH.

1-trygonometryczna

2-bezpośredniego rzutowania

3-wcięć

4-jednego punktu oporowego

5-projekcji laserowej

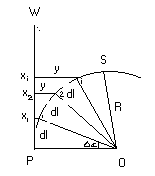
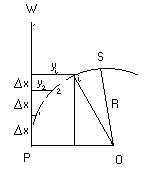
1)polega na wyznaczeniu wychyleń kątowych poszczególnych p-tów budowli w stos. do p-tu na najniż. poziomie. Pomiary z 3 stanow. symetrycznie wokół budowli. Odl. stanow. od bud. >1,5 h.

składowe wychylenia ze stanowisk:

wektory r1, r2, r3 są prostopadłe do kier. celowania ze stanow. 1, 2, 3. Wielkość wychylenia R i jego rzuty Rx i Ry oblicza się ze wzorów:

α1,α2,α3 azymuty linii celowania

azymut i wielkość wychylenia wylicza się ze wzoru:

błąd wychylenia wypadkowego:

wartość przybliżona bł. azymutu w-ychylenia wypadkowego oblicz-am:

Mając 3 składowe wychylenia r1, r2, r3 można wyznaczyć wychylenie wypadkowe met. analit.-graf. Langa. Szkicujemy rozmieszczenie stanow i nanosimy kierunki celu na najnizszy poziom. Od tych kierunków odkłada się wielkości r wyznaczone na i-tym poziomie. Przez końce takich odcinków prowadzimy proste równoległe do kierunków średnich. Proste tworzą trójkąt błędów. Geometrycny środek trójk. bł. określa położenie osi komina na danym poziomie. Wymiary trojk. błędów zależą od bł. pomiaru.

Budowle wysmukłe to bud. któ-rych wys. kilkakrotnie przewyższa szerokość. kominy przemysłowe, chłodnie kominowe, wieże, maszty telewizyjne, latarnie itp. Geod. obsł

obejmuje:

-projekt realizacji prac geodezyjnyc

-założenie geod. sieci realizacyjnyc

-wykonanie prac realizacyjnych

-kontrola w trakcie wznoszenia

-inwentaryz. powykon. i sporządze-nie dokumentacji powykonawczej

-obserwacja odkształceń w czasie montażu

Budowle wysm. mierzy się też w okresie eksploatacji. W celu wy-krycia odchyleń od pionowego i prostoliniowego przebiegu osi bu-dowli prowadzi się pomiary pio-nowości. Wykorzystuje się kilka metod.

OBL. MAS ZIEMNYCH

met. siatki kwadratów

Projektowana płaszczyzna dzieli obszar działki na części znajdujące się pod i nad tą płaszczyzną - inaczej na obszary wykopów i nasypów. Linia przecięcia pow-ierzchni terenu z powierzchnią projektowaną nazywa się linią robót zerowych. Na podstawie rzędnych istniejących i projekt-owanych, po odpowiednich obli-czeniach, otrzy-mujemy wielkość danego wykopu lub nasypu. Wzo-rem pozwalającym określić nam tę objętość jest wzór:

Pow. nasypu i wykopu określa się analitycznie, graficznie lub mecha-nicznie. Błąd wyznaczenia zależy przede wszystkim od długości boku kwadratu

met. przekrojów poprzecznych

Sposób ten jest powszechnie stosowany do obliczania robót ziemnych przy projektowaniu „budowli” o kształcie wydłużonym.

F₁, F₂ - pola powierzchni prze-krojów utworzonych z przecięcia terenu płaszczyznami pionowymi w miejscach przekrojów poprzecz-nych;

d - odległość między przekrojami

wzór ścisły na obliczenie objętości

DROGA

Przy projektowaniu wykorzystuje się mapy syt-wys gdzie nanosi się wszystkie elementy projektowanej trasy. Projekt wykonuje się w pł. poziomej i pion.

1)wykonanie projektu na mapie

2)tyczenie w terenie p-tu począ-tkowego i końcowego odcinka trasy oraz p-tów wierzchołkowych

3)pomiar długości odcinków kie-runków głównych oraz kątów zwr-otu stycznnych

4)na podst. parametrów określony-ch projektem obliczamy miary li-niowe i kątowe i wyznaczamy p-ty główne i pośrednie, sporządzamy szkice realizacyjne

5)wyzn. kilometraż wszystkich p-tów trasy

6)projektujemy niweletę i obl. łuki pionowe, wykonujemy przekroje poprz.

P-ty główne to p-ty styku łuku kołowego z prostymi głównymi tra-sy. Wyznaczenie terenowe polega na odłożeniu miar kątowych i liniowych od p-tu wierzchołko-wego (wyzn. na podst. osn. geod.) i kierunków głównych. W celu kon-troli prawidłowości wyznaczenia wyznaczać p-t środkowy S na 2 sposoby. Styczna główna t - dł. od W do P lub K. t = R tg (α/2);

WS = R (secα/2 - 1)

W celu bezpieczeństwa między prostą i łukiem stosuje się krzywą przejściową o zmiennej krzywiźnie. Jest to klotoida o parametrze a:

L R = a² = const. Łagodzi ona działanie siły odśrodkowej. Stoso-wane są 2 klotoidy symetryczne (jednakowe a) lub niesymetryczne (różne a). P-ty gł. klotoidy to p-ty styczności z prostą i łukiem koło-wym. Wzory:

τ = L/2R = L²/2a²

Xs = X - Rsinτ; H = Y - R(1-cosτ);

Ys = R + H = Y + Rcosτ;

T = X + Ytgτ; T_D = X - Yctgτ;

T_D = X - Yctgτ; N = Y/cosτ;

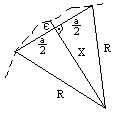
T_s = (R+H) tg ½γ; T_o = T_s + X_s;

Z = (R+H)(secγ/2 - 1)+H;

Z' = R(secα/2 - 1); patrz rysunek

Łuk koszowy - zespół krzywych (2 lub więcej łuków kołowych) o różnych promieniach; mają 1,2 lub więcej p-tów wspólnych i wspólne styczne w tych p-tach. P-ty gł. łuku koszowego to p-ty styczności z prostymi gł. i p-ty wsp. poszczegól-nych łuków. Wyznacza się je tak samo jak pojedynczy łuk kołowy.

α = α₁ + α₂;

t₂ = t₁cosβ+R₁sinβ-(R₁-R₂)sinα₂

R₂ = t₁sinβ-R₁cosβ-(R₁-R₂)cosα₂

cosα₂=(t₁sinβ-R₁cosβ-R₂)/(R₁-R₂)

α₁ = (200^g - β) - α₂

PM₁=M₁S₁=S₁N₁=N₁T₁=R₁tgα₁/4

TYCZENIE P-TÓW POŚREDN.

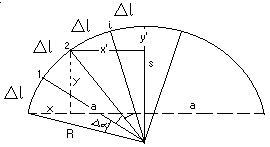
met. rzędnych od stycznej dla równych odcinków łuku

p-ty na łuku tyczy się w równych odstępach Δl. Dla tej wartości wyzn. kąt środk. Δα i wartości x i y poszczególnych p-tów pośrednich.

x_i=Rsin(i_*Δα); y_i = R[1-cos(i_*Δα)]

Δα^g = Δl _* ρ^g / R

met. rzędnych od stycznej dla równych odcinków na stycznej

zakłada się równe odcinki na stycznej (jednakowe wartości x), wyznacza się kolejne y.

y=R-√(R₂-x₂) lub y ≈ x² / 2R

TYCZENIE P-TÓW POŚREDN. KLOTOIDY

met. rzędnych od stycznej

wartości rzędnych i odciętych oblicza się w odniesieniu do klo-toidy jednostkowej a=1, później przelicza się wg wzoru

x=L - L⁵/40 + ...;y=L³/6-L⁷/336 +...

X = a x oraz Y = a y

met. biegunowa

określamy wartości odpowiednich kątów i długości, które później realizujemy w terenie.

x=L - L⁵/40 + ...;y=L³/6-L⁷/336 +...

ω = arc tg y/x; d = a√(x²+y²)

met. biegunowa w tyczeniu p-tów pośr. łuku kołowego

Podobnie jak przy tyczeniu klotoi-dy. Od stycznej KKP-W odkłada się kolejne wartości kąta biegu-nowego i w ten sposób (znając od-ległość do kolejnych p-tów pośr.) otrzymujemy szukane p-ty. Rysunk podobny do powyższego, tyle że między p-tami pośr. jest jeszcze cięciwa c. Δα=(Δl/r)_*ρ

d_i = 2Rsin(i_* (Δα/2))

c = 2R sin(Δα/2)

met. od przedłużonej cięciwy w łuku kołowym

łuk dzieli się na równe odcinki, od stycznej gł. odkłada się wart. x i prostopadle y. Później od cięciwy P-1 tak samo i mamy p-t 2. Cięciwa 1-2, odkł. x i y - mamy p-t 3 itd. Istnieje jednak możliwość wystą-pienia błędów wytyczenia (przeno-szenie błędów - źle wyznaczony p-t wpływa na kolejne p-ty).

ϕ=(Δl/2R)_*ρ; x₁=ccosϕ; x₂=ccos2ϕ

c=2Rsinϕ, y₁=csinϕ; y₂=csin2ϕ

met. rzędnych od cięciwy przy

p-tach pośr. łuku kołowego

Na cięciwie odkłada się wart. x a na prostopadłej wart. y. Wielkości wyznacza się pośrednio na podst. obliczonych a, s, x oraz y. x i y wyznacza się identycznie jak met. rzędnych od stycznej dla równych odcinków łuku.

a=Rsinα/2; s=R(1-cosα/2);

Δα=(Δl/R)ρ;

x_i'=Rsin(i Δα); y_i'=R[1-cos(iΔα)]

x = a - x'; y = s - y'

OPRACOWANIE PIONOWE DROGI

Przekrój podłużny wykonuje się na podst. niwelacji trasy lub na podst. aktualnej mapy syt.-wys. Na prze-krój terenu wkreśla się niweletę.

Załamania niwelety w pł. pionowej powinny być złagodzone przez zastosowanie łuków pionowych (wklęsłych lub wypukłych). Tyczenie jak w łuku poziomym - p-ty gł. i pośr.

Spadek niwelety i₁=ΔH₁/D_{1 *} 100%

oraz i₂=ΔH₂/D_{2 *} 100%

styczna t do łuku pion.

t = R/2 (i₁+i₂); WS = t²/2R

P-ty pośr. wyznaczono ze wzoru:

y_i ≈ x_i² / 2R

Obliczenie rzędnych ze wzorów

dla niwelety „pod górkę”

H = H_P + i_{1 *} x

dla niwelety „z górki”

H = H_k - i_{2 *} x

x - odl. danego p-tu od początku (lub końca) łuku. Należy też wyko-nać przekr. poprz. Są tam rzędne niwelety, korony drogi, szer. jezdni, pasa drogowego, głęb. rowów, itd. Wykonuje się je dla p-tów charak-terystycznych: p-ty gł., załamania niwelety, p-ty hektometrowe, skrz-yżowania, p-ty zmian wys. jezdni...

PRZENIESIENIE WYSOKOŚCI PRZEZ PRZESZKODY WODNE

Przy budowie mostów, zapór itp. zachodzi potrzeba przeniesienia wysokości przez przeszkody wod-ne. Stosuje się met. niwelacji geo-metrycznej lub trygonometrycznej przy użyciu tarcz bisekcyjnych.

met. niwelacji geometrycznej

Na łacie A wykonuje się odczyt wstecz, następnie (przy spoziomo-wanej osi celowej) celujemy na łatę na reperze B. Pomiarowy przesuwa tarczę bisekcyjną do momentu pokrycia poziomej kreski krzyża i środka tarczy. Należy wykonać kil-ka serii pomiarów by wyelimi-nować błędy. Z różnicy odczytów A i B otrzymuje się różnicę wyso-kości.

met. niwelacji trygonometrycznej

zasada przedstawiona jest na rysun-ku.

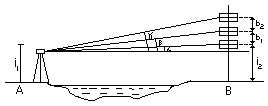
Przewyższenie ΔH można obliczyć trzykrotnie na podst. kątów α, β, γ. Chcąc zwiększyć dokładność wyz-naczenia ΔH należy przeprowadzić obserwacje jednocześnie z dwóch stanowisk po obu brzegach prze-szkody.

Na p-tach 2 i 4 ustawia się statywy z tarczami bisekcyjnymi i mierzy się wysokości tarcz nad p-tami oraz między tarczami. Teodolity ustawia się na p-tach 1 i 3. Obserwacje ką-tów pionowych wykonuje się jed-nocześnie. Mierzy się również kąty poziome.

Dokł. określenia różnicy wys. tą met. oblicza się ze wzoru:

m_h=√[(tgα+(1-K/r)D₀)m_do]² +

(d_om/cos²α)² + (d_om_K/2r)²

α - kąt pionowy

K - współczynnik refrakcji

r - promień kuli ziemskiej

d_o - odległość między p-tami

Na błąd przyrostu wysokości naj-większy wpływ wywiera błąd po-miaru kąta pionowego, wpływ od-ległości nie ma większego znacze-nia.

ΔH=i_t + Dtgα - i_s + D²[(1-K)/2r]

PROJEKTOWANIE PŁASZ-CZYZN BILANSUJĄCYCH

ROBOTY ZIEMNE

Każda płaszczyzna przechodząca przez środek ciężkości jest płasz-czyzną bilansującą roboty ziemne.

1)średnia wartość współrzędnych

X_S=Σ x_i/n Y_S=Σ y_i/n Z_S=Σ z_i/n

2)jeżeli pł. bilansująca ma zadany kierunek najw. spadku α i wart. najw. spadku k to r-nie płaszcz. to:

(kcosα)x + (ksinα)y - z + H_o = 0

H_o = - X_Skcosα - Y_Sksinα + Z_S

3)jeżeli projektowana płaszcz. ma przechodzić przez 2 p-ty

1 (x1, y1, z1) i 2 (x2, y2, z2) to

(x₁-X_S)kcosα + (y₁-Y_S)ksinα -

(z₁-Z_S) =0

(x₂-X_S)kcosα + (y₂-Y_S)ksinα -

(z₂-Z_S) =0

kcosα i ksinα dają tgα i liczymy α

4)jeżeli projektowana płaszczyzna ma przechodzić przez 1 dany p-t i ma określony max spadek wzdłuż kierunku α to mamy jedno r-nie;

(x₁-X_S)kcosα + (y₁-Y_S)ksinα -

(z₁-Z_S) =0

5)jeżeli projektowana płaszczyzna ma przechodzić przez 1 dany p-t i ma określony max spadek k to mamy jedno r-nie;

(x₁-X_S)kcosα + (y₁-Y_S)ksinα -

(z₁-Z_S) =0

i dołączamy r-nie sin²α+cos²α=1 i wyliczamy α

Projektowanie płaszcz. minimali-zujących roboty ziemne

a)dla każdego p-tu o znanych wsp. zestawiamy r-nie

v_i = (x₁-X_S)kcosα + (y₁-Y_S)ksinα -

- (z₁-Z_S)

r-nie te wagujemy proporcjonalnie do powierzchni otaczającej dany p-t i rozwiązujemy wg [pvv] = min

b)projektowana płaszczyzna ma zminimalizować roboty ziemne i zbilansować je. Wtedy dla każdego p-tu o znanych X i Y zestawiamy następujące r-nie aproksymujące:

v_i = e_X x_i + e_y y_i + z₀ - z_i

e_X - nachylenie pł. wzdłuż osi OX

e_y - nachylenie pł. wzdłuż osi OY

z₀ - przecięcie pł z osią OZ

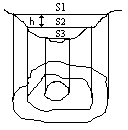
metoda przekrojów poziomych z mapy warstwicowej

V = h/2 Σ(S_i+S_i+1) + Δh/3_*S_n

met. siatki trójkątów

V = a²/2 _* 1/3(h₁+h₂+h₃)

met. p-tów rozproszonych

V = 1/3 S₁(h₁+h₂+h₃)

m_V²=(Vm_S/S)²+(S/3)²3m_h²+m_Vu²

m_Vu² = 0,6 Q S√b

Q - współczynnik bogactwa mikro- rzeźby (0,005 - 0,01)

b - średnia długość celowej

Na dokł określenia objętości skła-dają się następujące błędy:

m_K - bł. ukształt. pow. terenu

m_g - bł. zagęszczenia gruntów

m_W - wpływ dokł. materiałów wyj-ściowych.

m_K - bł. ukształt. pow. terenu

ε = R - x; x = √(R²-a²/4)

a - bok kwadratu w met. siatki kw.

Błąd obliczonej objętości ze wzglę-du na ukształtowanie terenu wynosi

m_Vu² = S ε_SR = n a² ε_SR

wpływ błędu zagęszczenia terenu

D=V_W/W_N; V_W=V_N D ±0,02D V_N

0,02D - ustalona tolerancja stopnia zagęszczenia gruntu; wg Polskiej Normy 0,9<D<1,15

wpływ dokładności materiałów wyjściowych

można to sprowadzić do wpływu dokładności wyznaczenia rzędnych terenu h.

1) V = S h₀

2) V = ΣS_i 1/KΣh_J

3) h₀ = V/S

4) h_J = h_J' ± m_hJ + u_J

Jeżeli do r-nia 3 podstawimy r-nie 4 to otrzymamy:

m_Vh = ±m₀√(S/K) + u₀S

u0 - bł. systemat. rzędnej wysokośc

m0 - bł. jednoznacznego określ. h

0,02m - niw. siatk.

0,10m - tachimetria

0,05m - p-ty rozproszone

0,05m - niw. przekrojów

0,20m - aerofotogrametria

TORY KOLEJOWE

Jedno-, dwu- i wielotorowe. Roz-jazdy są zwyczajne i krzyżowe. Rozjazd zwyczajny składa się ze zwrotnicy, torów łączących (wygię-tych wg promienia łuku kołowego), krzyżownicy. Typ rozjazdu podaje się symbolem, np. S49-300-1:9. S49- typ szyny, 300-promień toru odgałęźnego, 1:9-skos rozjazdu. Gdy od toru głównego odgałęziają się 2 tory w tę samą lub różne strony należy między początkami rozjazdów zaprojektować wstawkę prostej.

Projekt linii kolejowej obejmuje określenie niezbędnych miar kąto-wych i liniowych oraz sporządzenie szkiców umożliwiających terenową realizację projektu technicznego. W proj. tech. określa się parametry te-chniczne linii kolejowej.

połączenie torów równoległych rozjazdami o równych skosach

Wytyczenie polega na określeniu w terenie położenia p-tów środko-wych poszczególnych rozjazdów oraz p-tów pocz. i końcowych. Po-łożenie p-tu środk. wyznacza się w stosunku do istniejących torów lub osn. geod. i do założonego kilomet-rażu tego p-tu. Pozostałe p-ty wyznacza się przez odłożenie odpowiednich miar.

połączenie torów równoległych rozjazdami o różnych skosach

Opracowanie geodezyjne sprowa-dza się do określenia położenia p-tów głównych poszczególnych roz-jazdów. Punktem wyjściowym jest środek rozjazdu krzyżowego.

połączenie dwóch torów równoległych

Opracowanie geodezyjne polega na określeniu położenia p-tów głów-nych rozjazdu, wstawki prostej w oraz p-tów gł. łuku kołowego w torze odgałęźnym. Minimalną war-tość wstawki proste „w” oblicza się ze wzoru: w_min = V/6

V - max. prędkość taboru założona w projekcie

miara kontrolna c = √(b²+d²)

d - rozstaw torów, b=nd

t_proj = c - (p₁ + w_min)

t_prakt = R tg α/2

w_prakt = c - (p₁ + t_prakt)

Osmowę podst. linii kolejowych stanowi osn. państwowa I i II kl. Sieć ta jest dostatecznie gęsta by nie zachodziła potrzeba zakładania odrębnej osnowy podst. dla ter. ko-lejowych. Osnowę szczegółową do celów inwentaryzacji stanowi sieć p-tów osn. państw. III i IV kl. Ze względu na kształt szlaków kole-jowych najwłaściwszą metodą zakł-adania osnów jest met. poligonowa. Ciągi kl. III powinny być nawią-zane bezpośrednio do osn. I lub II kl., powinny znajdować się w gra-nicach pasa wywłaszczenia, w pob-liżu osi linii kolejowej. Ciągi po-winny być zbliżone do prostolinio-wych, dł. nie powinna przekraczać 3 km, dł. boku 100-300 m. dokł. pomiaru boku 1:5000, kąta ±10″

Osn. IV kl. - ciągi sytuacyjne lub linie pomiarowe, nawiązane do III kl. Dł. ciągu <2 km, linii pomiaro-wych 400m. Dł. boku ciągu sytu-acyjnego 50-350m, stosunek 2 są-siednich boków >1:3. Bł. pom. bo-ku 1:5000, kąta ±20″.

SUWNICE

Urządzenia do transportowania su-rowców i wyrobów w obrębie skła-dów lub hal produkcyjnych. Wy-magania techniczne szyn torów podsuwnicowych:

-prostoliniowe i równoległe;

-równooddalone (wg zał. projektu)

-we właściwej odległości od elem-entów konstrukcji hali czy estakady

-ułożone poziomo na jednej wyso-kości

Szyny suwnic układa się na belkach stalowych lub żelbetowych, te zaś oparte są na słupach nośnych lub wspornikach wystających ze słu-pów nośnych konstrukcji hali.

1)różnica poziomów główek szyn

± 10mm na podporach

± 15mm w przęśle

2)różnica poziomów główek w tej samej osi podłużnej b/1500 <10mm

3)max odchyłka w prześwicie

± 5mm (odch. od projektu)

4)odch. osi teoretycznej szyny od rzeczywistej ± 2,5mm

5)odchylenie czoła szyn w styku w pionie i poziomie max ± 1mm

6)max przerwa na łączeniu obu szyn ± 4mm

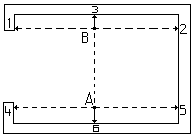
W terenie stabilizujemy 4 stanowis-ka osnowy kontrolej. Wyznaczamy współrzędne stanowisk, później rzędne p-tów zasygnalizowanych na belkach od płaszczyzn piono-wych I-II i III-IV.

Do pomiaru stosuje się łatę uk-ładaną poziomo i prostopadle do belek, tak by jej początek pokrywał się z oznaczonymi punktami ich osi Na podst. danych z pomiaru określa się odchyłki osi belek od projekto-wanych osi szyn. Oblicza się je w taki sposób, by jednocześnie uzys-kać dane do wyznaczenia wskaźni-ków montażowych szyn toru suw-nicowego. Wskaźniki te powinny leżeć na dwóch prostych równoleg-łych i odległych o projektowany rozstaw szyn. Należy je wpasować w teoretyczne osie. Przy wpasowa-niu stosuje się metodę spełniająca warunek minimum sumy kwadra-tów odchyłek osi belek od ich osi projektowanych. Opracowanie wy-konuje się dwiema metodami:

- analityczno - graficzna

- analityczna

analityczno - graficzna

Mając odczyty z łaty L i P obliczamy y_L i y_P praktyczne w układzie odniesienia (geodezyj-nym). Obliczamy środek toru dla każdego zasygnalizowanego p-tu [y₀=(y_L+y_P)/2] i obl. wartość śred-nią położenia osi toru [y_śr=(ΣY₀)/n]. Następnie obliczamy odchyłki ze wzoru: y₀-y_śr. Obliczone odchyłki odejmujemy od teoretycznej war-tości położenia osi toru (Y₀), po czym obliczamy Y_L=Y₀ - S/2 i Y_P=Y₀ + S/2. W końcu wyliczamy odchyłki osi belek w oznaczonych p-tach od wypośrodkowanych osi teoretycznych: V_YL=y_L-_YL; V_YP=y_P-Y_P oraz odchyłki rozstawu osi be-lek w poszczególnych przekrojach V_ROZ=V_YP-V_YL

met. analityczna

Różni się od anal-graf, że nie rysujemy wypośrodkowanej osi to-ru, ale obliczamy współczynniki tej osi oraz współrzędne Y0 przez podstawienie ich do odpowiednich r-ń poprawek. R-nia układa się wg wzoru: a_*i + b = y₀ - y_śr + v; i = d_i/i

a,b-współczynniki r-nia osi toru

di - odl p-tu od początku toru

d - odl. między sąsiednimi p-tami

y₀ - y_śr - wyraz wolny równania

v - poprawka

Obliczone odchyłki p-tów oznaczo-nych na osiach belek od wypośrod-kowanych teoretycznych osi szyn wykorzystywane są w ten sposób, że odkłada się je od wspomnianych p-tów z odwrotnym znakiem, uzys-kując na belkach miejsca wskźni-ków do montażu szyn.

SZYBY DŹWIGOWE

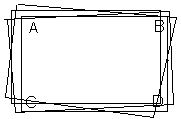
Jednocześnie z pomiarem kontrol-nym po montażu ścian każdej kon-dygnacji należy wykonać pomiar kontrolny zmontowanych szybów dźwigowych. Wyniki tego pomiaru przedstawia się na jednym szkicu z wynikami pomiaru ścian, by przed montażem następnej kondygnacji można było wykonać korektę w dalszym montażu. Po wykonaniu stanu surowego budynku wykonuje się pomiar odchyłek ścian szybów dźwigowych przed montażem dź-wigów. Celem jest stwierdzenie za-chowania dopuszczalnych odchyłek szybów oraz uzyskanie danych do osadzenia prowadnic dźwigowych. Dla szybów montowanych z prefa-brykatów wykonuje się najczęściej pomiar pionowości i rozstawów ścian z osnowy, którą stanowi za-kładana na górze lub dole dwupun-ktowa baza AB.

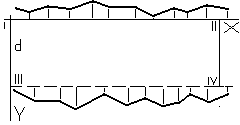
W p-tach A i B ustawia się pion opt. i 2-krotnie odczytuje na łacie odległości od pionowej osi celowej do ścian szybu. Odczyty wykonuje się dla p-tów 1-6 na każdym poziomie roboczym. Dla każdego przekroju oblicza się różnice między odczytami na poszczególnych kondygnacjach a średniąą arytm. wszystkich odczytów (dopasowaną do wymiarów projektowych szybu).

wpasowanie osi prowadnic dźwi-gowych i optymalizacja wpaso-wania

Czynność polega na znalezieniu max prostopadłościanu, który da się wpasować w przestrzeń ograniczo-ną ścianami szybu. Wpasowanie wykonuje się met. graficzną lub analityczną.

metoda graficzna

Osnową są 4 p-ty wierzchołkowe prostokąta o znanych współrz. Wszystkie przekroje orientuje się względem prostokąta i nanosi na jeden rysunek. Na kalkę nanosi się osie prowadnic i wpasowuje się w rys. przekrojów.

met. analityczna

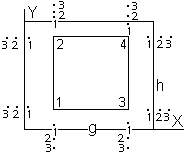
Określa się optymalne płaszczyzny w których zamontuje się prowadnice. Podst. opracowania jest met. parametryczna z warun-kami wiążącymi parametry. Obli-czenia wykonuje się w ukł., gdzie osiami XY są krawędzie ścian szybu w piwnicy budynku. W stosunku do tych osi odnosi się krawędzie ścian dla każdej kon-dygnacji. Kolejność obliczeń;

1)obl x i y p-tów obserwowanych

2)ułożenie r-ń poprawek

X_i^obs + V_X = X_i^wyr

Y_i^obs + V_Y = Y_i^wyr

3)nałożenie na niewiadome warun-ku równoległości i prostopadłości

X₃^W - X₁^W = g war. równoległości

X₄^W - X₂^W = g prostych 1-2 do 3-4

Y₂^W - Y₁^W = h oraz 2-4 do 1-3

Y₄^W - Y₃^W = h

warunki prostopadłości

X₂^W - X₁^W = 0

X₄^W - X₃^W = 0

Y₄^W - Y₂^W = 0

Y₃^W - Y₁^W = 0

Optymalizacja to ponowny pomiar poprawności wykonania pionem o-ptycznym (gdyż montażyści używ-ają ciężkich pionów sznurkowych).

PRZENOSZENIE WSKAŹNI-KÓW KONSTRUKCYJNYCH

Przed przystąpieniem do obsługi geodezyjnej kondygnacji powta-rzalnych i wyznaczaniu wskaźni-ków konstrukcyjnych na poszcze-gólnych poziomach roboczych na-leży sporządzić szkic tyczenia, za-wierający rozmieszczenie osi konst-rukcyjnych zgodnie ze szkicem do-kumentacyjnym oraz osnowe bu-dowl.-montaż. Osnowa ta będzie służyć do przenoszenia osi konst-rukcyjnych na poszczególne kondy-gnacje.

met. stałej prostej

a)stawiamy teodol. na p-cie linii bazowej osnowy bud-mont., celuje-my na tarczę na końcu tej linii

b)poziomujemy teodol. przy każ-dym pomiarze

c)układamy łatę na stropie kondyg-nacji roboczej i ustawiamy ją pro-stop. do płaszcz. celowania

d)łatę ustawiamy tak, by obraz tar-czy sygn. znalazł się na pionowej kresce siatki celowniczej teodol.

e)zaznaczamy na stropie tyczony punkt. Czynności wykonujemy w 2 poł. lunety.

1)jeśli O_K=O_P to O_K'-ΔK=O_P'-ΔP

2)ΔK = ΔP/d_{P *} d_K

poprawki trasowania

ΔP = [(O_K'-O_P')/(d_K-d_P)] _* d_P

ΔK = [O_K'-O_P'] + ΔP

analiza dokładności

1.bł centrowania teodol. 0,4mm

2.bł centrowania sygnału 0,4mm

3.niepionowość osi obr teod 0,9mm

4.bł celowania na tarczę 0,3mm

5.bł wprowadzenia sygn. w oś celo-wą 0,4mm

6.bł oznaczania wskaźnika 0,8mm

7.inne błędy 0,3mm

m = √(m₁₂+m₂²+...m₇²) = ± 1,4mm

metoda rzutowania

Wyznacza się osie konstrukcyjne lub linie równoległe do tych osi dla ścian zewn. i wewn. Przenosi się też tą met. wszystkie typy osnowy wewn. na kondygnację roboczą.

1)teod. stawiamy na stanow. pozio-mujemy, celujemy pionową kreską na wskaźnik wyjściowy na bud.

2)w 2 poł. lunety wyzn. wskaźnik na krawędzi stropu wg kreski pion.

3)każdorazowo poziomujemy teod.

4)analogicznie wyzn. wskaźnik z drugiej strony budynku

5)wtyczyć teod. w linię przeniesio-nych wskaźników i za pomocą łaty realizacyjnej wyznaczamy wskaźni-ki ścian zewn. ANALIZA:

niepionowość osi obr. teod. 0,9mm

bł. celowania 0,3mm

bł wprowadzenia sygn w płaszcz. rzutowania 0,4mm

oznacz. wskaźnika na strope 0,8mm

m² = m₁²+...m₄² = 1,3mm

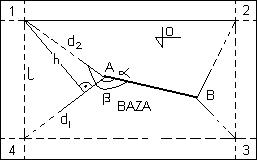
metoda biegunowa

l² = d₁² + d₂² - 2d₁d₂cos(β-α)

m_L² = cos²αm_d1² + cos²αm_d2² + h²m_β² + h²m_α²

ANALIZA

bł centrowania pionownika 0,3mm

bł poziomowania libelli 0,1mm

bł odczytu podziałki 0,7mm

bł oznaczenia p-tu na tarczy 0,5mm

m = 0,5mm

przy n kondygnacjach m_n = 0,5√n

TYCZENIE DŁUGICH PROS-TYCH PRZEZ PRZESZKODY

1.Odcinek do 2km tyczymy przy pomocy teodolitu. Na końcu odcin-ka stawiamy sygn. Tyczymy od p-tu najdalszego do najbliższego. P-ty w odl. <=300m

2.Dł. odcinka do 5km to tyczymy etapami jak w met. nr 1. Wyzna-czamy p-t najdalszy i pośrednie na tej linii, potem przenosimy teodolit na ten najdalszy p-t i powtarzamy czynność.

3.Mniej - więcej w pobliżu środka prostej wybieramy p-t, mierzymy na nim kąt wierzchołkowy i obli-czamy przesunięcie d, które należy wykonać, by p-t znalazł się dok-ładnie na tyczonej prostej.

4.Proste dłuższe od 5km - tyczenie etapami (2) lub punktami posiłko-wymi (3).

tyczenie w terenie falistym

1.Jeśli z p-tu pocz. widać końcowy to tyczymy najdalszy p-t pomocni-czy. Jeśli z dalekiego p-tu pomocni-czego nie widać końcowego to sto-sujemy met. przedłużeń (na najdal-szym stawiamy teodolit, celujemy na p-t pocz. przechylamy przez ze-nit i wyznaczamy p-t najdalszy lub końcowy. Robimy to 2-krotnie).

2.Jeżeli nie widać p-tu końcowego, a istnieje osnowa geod., to po nawi-ązaniu do niej kierunku trasy obli-czymy współrzędne p-tu pocz i koń

3.Jeśli nie widać p-tu P i K, ale w pobliżu w terenie istnieje sieć poli-gonowa, to p-ty kierunkowe można wyznaczyć przez obliczenie prze-cięć prostej PK z bokami poligo-nowymi albo przez obliczenie do-miarów prostokątnych lub bieguno-wych do określonych p-tów.

tyczenie przez przeszkody

1.Obywa się w sposób pośredni. Jeśli p-ty P i K są wzajemnie niewi-doczne to obok przeszkody wyzna-czamy linię pomocniczą PL i mie-rzymy odcinek KL i kąt α na stano-wisku L. Póńiej z zależności mate-matycznych wyznaczamy p-ty pośr-ednie linii PK.

2.Jeżeli przeszkoda rozciąga się na dużej przestrzeni (np. las) i celowa-nie z P na K jest niemożliwe to kie-runek prostej tyczy się w przybli-żeniu przez wyznaczenie azymutu PK i tyczenie go w terenie za po-mocą busoli. Sposób jest dobry gdy PK<1200m.

Dokładne wytyczenie trasy można wykonać po założeniu specjalnej osnowy wokół przeszkody. Dla krótszych odcinków może to być osnowa poligonowa, dla długich - specjalna sieć triangulacyjna.

OSNOWY REALIZACYJNE

Sytuacyjne(XY),wysokościowe(H), przestrzenne(XYH). Wszystkie dzi-elą się na podstawowe - szczegół-owe - budowlano-montażowe. Osn. dzielą się na osn. dowolnego kształ-tu, regularne, układ baz, sieci wyd-łużone, zakładane techniką GPS.

Podst. osn. real. wiąże tyczoną inw-estycję z otaczającym terenem i uz-brojeniem. Szczegółowa osn. real. służy do bezpośredniego oparcia pomiarów realizacyjnych. Podst. os real. to pozioma osn. II kl i wysokościowa II kl. Projektowanie to 1)czynności wstępne. 2)prace projektowe. A.D.1)analiza danych wyjściowych (inform. o terenie, os-nowie, plan realizacyjny inwestycji, założenia techniczne i dokładnoś-ciowe) projektu i przegląd stoso-wanych rozwiązań danego zadania. A.D.2)projektowanie obejmuje 3 etapy analiz i ustaleń (geometria sieci i obserwacje wiążące; dokład-ności obserwacji; szczegóły realiza-cji i opracowania wyników). Do wykonania projektu sieci niezbędny jest plan realizacyjny danej inwes-tycji - zawiera rozmieszczenie wszystkich zaprojektowanych obie-któw i urządzeń na tym terenie. Projektując sieć należy tak usytu-ować jej p-ty w terenie, by służyły do pomiarów przez cały okres reali-zacji inwestycji.

dokładności tyczenia lokalizacyjnego

określa się na podst. dopuszczal-nych odchyłek realizacji p-tów o-biektów. Są to bł. tyczenia p-tów w terenie i bł. czynności budowla-nych. Wartości średnich bł. tycze-nia p-tów, długości lub kierunków pozwalają na określenie dokładno-ści pomiaru sieci realizacyjnej. Ty-czenie to czynności pomiarowe ma-jące na celu wskazanie i utrwalenie w terenie lub na obiekcie zespołu p-tów o założonych z góry położe-niach w stosunku do p-tów ozna-czonych w terenie lub na obiekcie i przyjętych jako p-ty odniesienia. Tyczenie 2-etapowe - wytyczenie przybliżonej pozycji P° p-tu P i po wprowadzeniu niewielkich popra-wek tyczenia dX_t, dY_t ostatecznego położenia tego p-tu. Tyczenie 1-etapowe - wytyczenie nominalnej pozycji p-tu P bez posługiwania się utrwaloną pozycją przybliżoną P°. Pozycję p-tu znaj-dujemy przez odłożenie kątów i/lub odległości stanowiących elementy zaprojek-towanej konstrukcji tyczenia. O-gólne zasady ustalania dokładności: m_td² = m_fd² + m²_d(α,d) lub inaczej

m_td² = m₀²(F_d^T Q F_d) + m²_d(α,d)

m₀ - śr bł. jednostkowy po wyrówn

Q - macierz współczyn. wagowych

F_d - mac. funkcyjna wiążąca dł. ty-czonego odcinka ze współrz odpo-wiednich p-tów osnowy.

m_fd² - bł. średni wynikający z dokł. osnowy

m²_d(α,d) - bł. średni wynikający z dokładności tyczenia

m_α²=m_Ct²+m_Cs²+m_ς²+(m₀²+m_C²)/S

S - ilość serii

m_C = bł. celowania m_C=60``/G

m₀ - bł. odczytu

m_ς - bł. spowodowany niepoziomo-wością limbusa

m_ς = i (tgβ_P*sinδ_P - tgβ_L*sinδ_L)

i - kąt odchylenia linii najwięk-szego spadku płaszczyzny limbusa od poziomu

β - kąt nachyl. osi cel do poziomu

δ - azymut osi celowej

1.ustala się jakie i ile obserwacji w sieci należy wykonać

2.ustalamy dokładność i ilość serii pomiaru (dobór instrumentu do po-miaru)

Analizę dokładności można wyko-nać z uwzględnieniem błędów p-tów nawiązania lub bez

dokładność w met siatki kwadratów

ze wzoru Gauss-a

m_V²=(Vm_S/S)²+(S/3)²3m_h²+m_Vu²

met. przekrojów podłużnych

1. V = d/3 (F₁ + F₂ + √(F₁F₂))

2. Simpson

V = d/6 (F₁ + F₂ + 4F_ŚR)

3. wzór Czepsena

V = d/2(F₁+F₂) - d/6 i (h₂-h₁)

i - spadek terenu

Plan realizacyjny

część opisowa to: przedmiot i zak-res inwestycji; opis istniejącego za-gospodarowania terenu; zestawie-nie danych o przydatności gruntów do celów budowy; infrastruktura i uzbrojenie itp. Dla celów projekto-wych ważne są 2 cechy podkładów mapowych: dokładność i szczegół-owość. Dokładność graficzna to bł. położenia szczegółów sytuacyjnych w stosunku do poł. najbliższ. p-tu osn. geod. I grupa dokł. 0,3mm w skali mapy; pozostałe 0,6mm. Do-kł. wzajemnego poł. 2 p-tów 0,4-0,8mm w sk. mapy. Geodezyjne o-pracowanie planu realiz. i proj. techn: met. graf., analit.,anal-graf. 1. ustalenie lokalnego ukł. wsp. osn. realiz. i obl. wsp. 2. wyz-nacz. danych geod. do określenia transf. X' Y' planu realiz. na wsp. w ukł. geod. 3. obl. XYZ p-tów ok.-reślających główne elementy planu realiz. 4. obl. bł. elem. liniowych i kątowych służących do wyznacz. p-tów. 5. obl. elem. kontrolnych. Projekt techn. obiektu budowla-nego: 1. sprawdzenie danych licz-bowych proj. 2. obl. p-tów głów-nych obiektu w ukł. planu realiz. 3. przeliczenie na ukł. geod. 4. obl. elem. geod. służących do wytycz-enia obiektu w terenie. 5. wykaz geod. elem. kontrolnych. Wyniesienie proj. planu realiz. w teren: dokumentacja: zatwierdzony plan realiz. - proj. tech. obiektów budowl. - szkic dokum - dziennik bud - szkic tyczenia - dziennik nadzoru autorskiego - warunki tech - dokumentacja proceduralna. Szkic dokumentacyjny: elem. osn. realiz - usytuowanie gł i szczegól osi konstuk w nawiązaniu do osn - dane wyjściowe nawiąz geod wz-ględem osn real - odległ między p-tami osn real a osiami budowli - nr zlecenia, projektu - nazw wykona-wcy, data. Szkic tyczenia powstaje po pomiarze (zakończeniu realizacji szkicu dokumentacyjnego), nanosi się wszystko co zauważone było podczas realizacji. Met. niwelacji trygonometrycznej ΔH = d tgα

m_ΔH² = m_d²tg²α + (d²m_α² / β²cos⁴α)

m_α = ½ m_d/d ρ sin2αβ

Prace realizacyjne 1. geod opraco-wanie planu realiz oraz proj obiek-tów budowl 2. tyczenie lokaliza-cyjne ob. budowl 3. tyczenie szcze-gółów 4. pomiary kontrolne 5. po-miary przemieszczeń i odkształceń podczas budowy 6. pomiary powy-konawcze. Tyczenie lokalizacyj-ne: określenie poł. względem osn realiz elementów projektowanego obiektu i zaznaczenie ich w terenie w taki sposób, by wytyczone p-ty mogły być wykorzystane przy wy-konaniu robót bud-montażowych. Met. tyczenia lokal. biegunowa, wcięcia kątowego w przód, ortogonalna, przecięć.

INWENTARYZACJA PRZEW-ODÓW PODZIEMNYCH

Bezpośrednia (przed zasypaniem) i pośrednia (pomiar rzędnej osi prze-wodu) tachimetrem. Dzieli się na szczegółową i zbiorczą, a oprócz tego inwent. może być schematycz-na lub bramowa. Metody inwent pośredniej: indukcyjna (wykorzys-tuje zmienne pole elektryczne oraz generator drgań i nadajnik) 2. gal-waniczna (podłączenia przewodu). Met galwaniczna jest nieznacznie dokładniejsza od indukcyjnej. Wyzn poł przewodu met ind.

1. sygnał w momencie natrafienia na przewód (nadajnik wysyła fale w promieniu 5m, ciągle przesu-wamy nadajnik i w ten sposób wykrywamy przewód) 2. siatka kwadratów - nadajnik na kolejnych narożnikach siatki 3. wyzn kierun-ku podłączenia lub załamania prze-wodu 4. wyzn poł przewodów le-żących blisko siebie (gdy d>1m można wyzn poł, gdy d<1m - poł przybliżone).

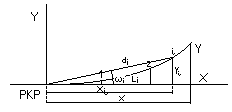
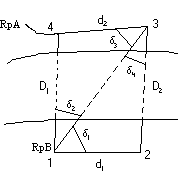
1. Budownictwo wieżowe, wyznaczenie odchyleń od pionowości metodą kątową wraz z analizą dokładności.

metoda kątowa = metoda kierunkowa = metoda dwusiecznej

Pomiar polega na wyznaczeniu kierunków stycznych (lewej K_L i prawej K_P) do obiektu w każdym z przekroju, z każdego stanowiska obserwacyjnego.

Średnia z każdej pary kierunków określa położenie osi budowli w poszczególnych przekrojach:

K=

Natomiast
jest różnicą między położeniem osi na poziomie i oraz na poziomie najniższym - najbliższym podstawie budowli ( przyjmowany za poziom zerowy) i pozwala z zależności

d - odległość między stanowiskiem a osią obiektu

obliczyć składowe wychylenia osi budowli od pionowości w kierunku prostopadłym do celowych z poszczególnych stanowisk obserwacyjnych

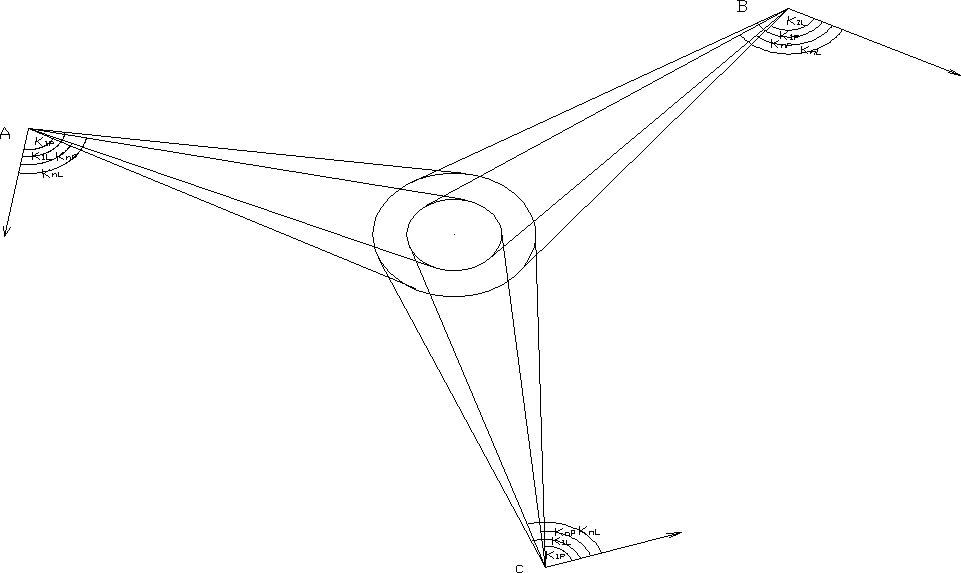
Liczba stanowisk od 2 do 5, najlepiej 3, a kąt między poszczególnymi stanowiskami a kierunkiem do osi obiektu

, n - liczba stanowisk obserwacyjnych.

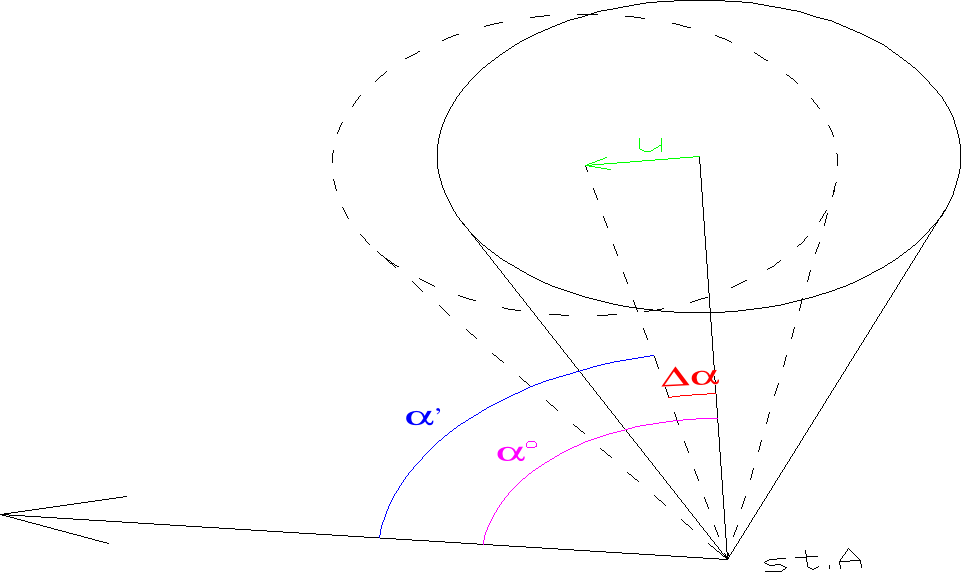
α⁰ - kąt miedzy kierunkiem nawiązania a osią obiektu tuż przy podstawie(poziom zerowy)

αⁱ - kąt między kierunkiem nawiązania a osią budynku na danym poziomie

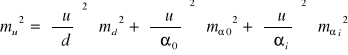
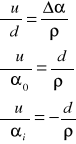
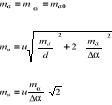
Budownictwo mieszkaniowe. Co to montaż wymuszony i swobodny?, rysunek.

Łączenie elementów prefabrykowanych w zespoły konstrukcyjne (montaż) może być realizowane w różny sposób .Spośród różnych sposobów wyróżnia się:

Montaż swobodny - montaż elementów prefabrykowanych wykonywany na styk prosty, bez pomocy części łączących ograniczających wielkości odchyłek montażu, pozwalający na swobodne, wzajemne przesunięcia względem siebie montowanych elementów.

Na rys. Zasada montażu swobodnego: a) montaż elementów płytowych, b) montaż elementów słupowych

Montaż wymuszony - montaż elementów prefabrykowanych, wyposażonych w płaszczyznach stykowych z złącza montażowe ograniczające odchyłki montażu, wyznaczające z dużą dokładnością miejsce usytuowania elementów w konstrukcji budynku.

Na rys. Zasada montażu wymuszonego: a) montaż elementów płytowych na występach rektyfikacyjnych, b )na śrubach, c) montaż elementów słupowych na śrubach.

Piotr Zyśk grupa 3, rok III

PRACE ZIEMNE

Wpływ ukształtowanie powierzchni terenu na dokładność określenia objętości

Błędy określenia objętości gruntów.

Można wyróżnić dwa podstawowe źródła błędów określenia objętości:

1. błędy pomiarów i opracowań map, na które składają się:

2. błąd odwzorowania terenu

3. błąd pomiaru rzeźby terenu

1. błąd opracowania mapy warstwicowej

4. błędy obliczania objętości, wynikające z przyjętego sposobu obliczeń

Błąd odwzorowania terenu

Powierzchni terenu nie można odwzorować wiernie (izometrycznie). Każdy pomiar rzeźby terenu stanowi aproksymacje powierzchni terenu powierzchnią topograficzną, czyli powierzchnią określoną zbiorem punktów o znanych współrzędnych w przyjętym układzie odniesienia. Geodeta, dokonując pomiaru powierzchni terenu dzieli ją na szereg płaszczyzn, najczęściej trójkątnych, przez wyznaczenie współrzędnych wierzchołków figur. W rzeczywistości pomiędzy trzema punktami tworzącymi płaszczyznę rozpięty jest pewien płat powierzchni terenu o nieregularnej krzywiźnie. Punkty powierzchni terenu mogą względem danej płaszczyzny przyjmować różne położenia:

1. wszystkie nad płaszczyzną (powierzchnia wypukła)

2. wszystkie pod płaszczyzną (powierzchnia wklęsła)

3. 
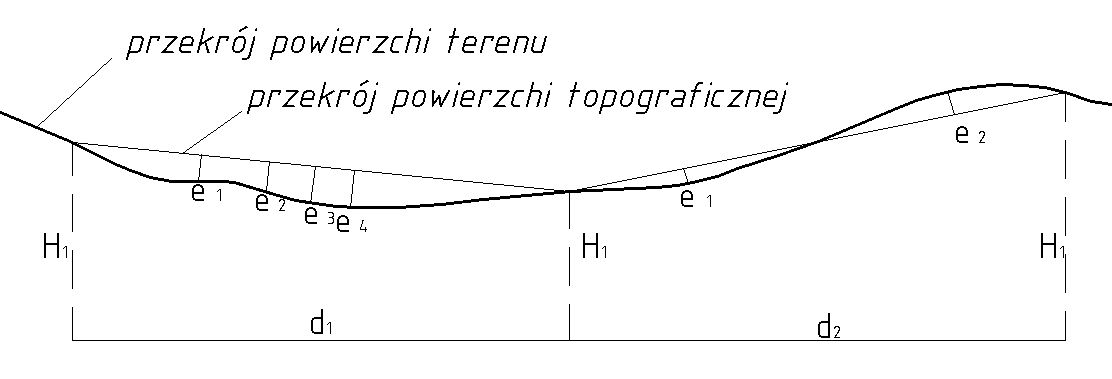
   cześć punktów nad, część pod, a wobec tego część również na płaszczyźnie

Odległości e_i powierzchni terenu zmieniają się od 0 do e_max , gdzie e_max - największa odległość pomiędzy powierzchnią terenu a daną płaszczyzną.

Ze względu na nieskończoną ilość punktów na powierzchni, średnią odległością e₀ będzie wartość oczekiwana E(e_i), a zatem objętość bryły V_i, utworzonej przez płat powierzchni terenu i daną płaszczyznę pola S_i będzie: V_i = E(e_i)S_i

W rozpatrywanym punkcie odległości e_i są błędami prawdziwymi odwzorowania terenu i jak wiadomo mogą być z dostatecznym przybliżeniem określone na drodze pomiaru. Z uwagi na skończoną liczbę punktów powierzchni, w których możemy dokonać pomiaru, wartość oczekiwaną E(e_i) zastąpimy średnim błędem odwzorowania terenu:

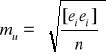
gdzie e_i - odległość pomiędzy powierzchnią terenu a płaszczyzną powierzchni topograficznej, pomierzona w punkcie i z dokładnością umożliwiającą uznać ją za błąd prawdziwy; n - liczba pomierzonych odległości.

Wpływ błędu odwzorowania terenu na dokładność obliczenia objętości gruntu będzie zależna od charakteru terenu. Jeżeli teren jest zróżnicowany pod względem ukształtowania powierzchni, tzn. gdy wymienione pod (a), (b), (c) położenia powierzchni terenu względem płaszczyzny topograficznej występują w przybliżeniu z jednakową częstotliwością na całym obszarze objętym robotami ziemnymi, wówczas ze względu na jednakowe prawdopodobieństwo wystąpienia dodatnich i ujemnych błędów odwzorowania terenu e_i można napisać:

gdzie:

m_Vz - wpływ błędu odwzorowania terenu na dokładność obliczenia objętości gruntu

m_z - średni błąd odwzorowania terenu

S₀ - pole średniego trójkąta utworzonego przez punkty pomiaru rzeźby terenu

n - liczba trójkątów na obszarze o powierzchni S

32.Pomiary kolejowe. Rozjazd prosty.

Do urządzeń techniczno-kolejowych między innymi zalicza się rozjazdy i skrzyżowania. Urządzenia te umożliwiają przejazd pociągów z jednego toru na drugi lub pozwalają na prowadzenie pociągów po danym torze, mimo iż krzyżuje się on z innym.

Rozjazdy można podzielić na 2 podstawowe typy: zwyczajne (proste) i krzyżowe.

Rozjazd zwyczajny składa się z 3 zasadniczych części:

• zwrotnicy złożonej z dwu wzajemnie połączonych iglic, których przesunięcie nadaje pociągowi określony kierunek;

• torów łączących wygiętych według promienia łuku kołowego, odpowiadającego temu rozjazdowi;

• krzyżownicy

Najważniejszymi częściami rozjazdu są zwrotnica i krzyżownica, które zapewniają właściwy i bezpieczny przejazd taboru.

W rozjeździe wyróżnia się dwa kierunki torów: kierunek toru zasadniczego (prosty) oraz kierunek toru odgałęźnego (w łuku). Za początek uważa się styk szyn przed iglicą, a za końce rozjazdów - styki szyn znajdujące się bezpośrednio za krzyżownicą w torze odgałęźnym i zasadniczym. Na mapie sytuacyjnej, gdzie zamiast torów są osie, rozjazd będzie zaznaczony w sposób schematyczny.

Rozjazd wyznaczają punkty zaznaczone na osi toru zasadniczego i odgałęźnego. Będą to: punkt A, odpowiadający początkowi rozjazdu, punkty P i P', odpowiadające końcom rozjazdu, oraz punkt M, zwany środkiem rozjazdu, który powstaje z przecięcia osi toru zasadniczego z przedłużonym kierunkiem prostym toru odgałęźnego. Punkt M zwany jest również punktem geometrycznym rozjazdu. Punkty P i P' łączy się linią prostą, a powstały trójkąt PMP' kreskuje się lub cieniuje. Kąt α, zawarty między kierunkami obydwu osi, nosi nazwę kąta rozjazdu. Wyrażany jest najczęściej za pomocą ułamka 1:n, zwanego skosem rozjazdu. Promień łuku toru odgałęźnego jest zależny od skosu rozjazdu. Im skos większy, tym promień powinien być mniejszy i odwrotnie. Odległości od punktu początkowego do środka rozjazdu (odcinek a) oraz od środka rozjazdu M do punktów końcowych P i P' (odcinki p i p') zależne są od typu rozjazdu i jego konstrukcji.

Typ rozjazdu podawany jest najczęściej w skróconej formie, np. S42-265-1:10, gdzie S42 oznacza typ szyn zastosowany do konstrukcji rozjazdu, 265 - promień toru odgałęźnego, 1:10 - skos rozjazdu.

Rozjazdy zwyczajne mogą być prawo- lub lewozwrotne, w zależności od kierunku toru odgałęźnego w stosunku do toru zasadniczego.

Tyczenie rozjazdów.

Rozjazdy tyczone są najczęściej od osi uprzednio wyznaczonego toru. Wytyczenie rozjazdu polega na wyznaczeniu w terenie punktów A, M, P i P'. Położenie punktu A można wyznaczyć na podstawie miar podanych w projekcie, lokalizujących ten punkt względem innych szczegółów, np. względem początków krzywych przejściowych lub łuków, załomów profilu, wag wagonowych, przejazdów itp.

Punkty M i P wyznacza się przez odłożenie po osi toru, począwszy od punktu A, najpierw odcinka a, a następnie p. Wyznaczone punkty A, M i P muszą leżeć na jednej prostej. Punkt P' można wyznaczyć metodą prostokątną, za pomocą wielkości x i y, przy czym

x = p'cos α; y = p'sin α;

lub wcięciem liniowym, za pomocą wielkości p' i e.

Innym sposobem wyznaczenia punktu P' jest odłożenie wielkości p' wzdłuż uprzednio wytyczonego kierunku toru odgałęźnego. Wielkości a, p, p' dla danego typu rozjazdu podane są w tablicach rozjazdów.

14. Wyróżniamy

5 metod tyczenia wskaźników konstrukcyjnych:

1. metoda przecięć kierunków,

2. metoda rzutowania,

3. metoda tyczenia od stałej prostej,

4. metoda biegunowa,

5. metoda laserowo - optyczna.

Do tyczenia wskaźników konstrukcyjnych na kolejnych kondygnacjach powtarzalnych stosuje się, zależnie od przyjętej metody obsługi geodezyjnej, następujące rodzaje osnów:

1. osnowa budowlano- montażowa zewnętrzna (dla stanowisk teodolitu poza budynkiem) zakładana w celu tyczenia wskaźników metodą stałej prostej, rzutowania lub przecięć kierunków;

2. osnowa budowlano- montażowa wewnętrzna (dla instrumentu ustawionego na stropie budynku) wyznaczana za pomocą optycznych przyrządów do pionowania lub wyznaczania teodolitem metodą wtyczania się w określone kierunki.

Metoda przecięć kierunków najczęściej stosowana jest do wyznaczenia osi stóp fundamentowych i wskaźników na półsłupkach parteru.

Podczas realizacji budynków niskich jednokondygnacyjnych i pięciokondygnacyjnych oraz budynków o średniej wysokości do XI kondygnacji tyczenie osi montażowych lub wskaźników konstrukcyjnych odbywa się wprost z ramy geodezyjnej metodą bezpośredniego rzutowania bądź metodą tyczenia stałej prostej, albo metodą przecięć kierunków (rys. ).

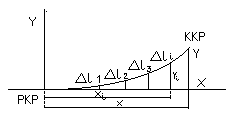
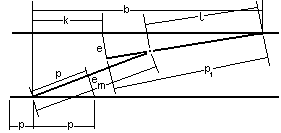
Tyczenie wskaźników montażowych metodą biegunową odbywa się z punktów P i Q przenoszonych na strop kondygnacji roboczej za pomocą pionowników (rys. ). Metoda ta polega na tym, że poszczególne punkty 1', 2', ..., n' osi montażowych na kolejnych kondygnacjach wyznacza się przez odkładanie od punktów końcowych bazy P_i i Q_i stałych kątów α₁, α₂, α₃,..., α_n oraz odcinków l₁, l₂, l₃, ..., l_n wcześniej pomierzonych na poziomie zerowym. W tym celu na każdej kondygnacji nad punktami P_i, Q_i ustawia się teodolit, który powinien być starannie zorientowany, zawsze na ten sam dobrze widoczny i odległy cel I, II ... itd. Następnie od kiedy na kierunkach wyznaczonych przez ramiona wymienionych kątów odkłada się odcinki l₁, l₂, ..., l_n, których końce określają położenie punktów osiowych 1', 2', ..., n'.

W związku z powyższym podczas lokalizacji punktów końcowych bazy pomiarowej P₀ i Q₀ powinny być spełnione następujące warunki:

• z punktów końcowych bazy (P₀ i Q₀) muszą być dobrze widoczne na wszystkich kondygnacjach co najmniej po dwa stałe punkty służące do zorientowania teodolitu (I, II, III ...),

• punkty P₀ i Q₀ powinny być tak zlokalizowane, aby odległości do tyczonych punktów osi montażowych nie przekraczały długości taśmy 20-metrowej,

• z uwagi na to, że punkty końcowe bazy pomiarowej P_i oraz Q_i spełniają funkcję stanowisk teodolitu, lokalizacja ich musi być taka, aby osoba obsługująca instrument miała zapewnione warunki bezpiecznej i dostatecznie wygodnej pracy.

Postęp w zakresie automatyzacji obliczeń pozwala również na pewną modyfikację tej metody, polegająca na tym, że na stropie kondygnacji roboczej możemy wybrać dowolnie stanowiska P i Q, a następnie metodą wcięcia wstecz (celując na punkty I, II i III) wyznaczamy współrzędne tych stanowisk. Ze współrzędnych stanowiska (P lub Q) i współrzędnych wskaźników konstrukcyjnych obliczamy wielkości kątów α i wielkości liniowe l do tyczenia tych wskaźników.

33. Pomiary kolejowe. Połączenia torów rozjazdami o równych skokach.

Kąt α zawarty między kierunkiem osi toru zasadniczego a kierunkiem osi toru odgałęzionego, nosi nazwę kąta rozjazdu. Wyrażany jest najczęściej za pomocą ułamka 1:n, zwanego skosem rozjazdu. Patrz rysunek a) w pytaniu 32

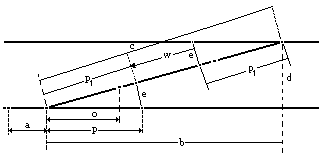
Połączenie dwóch torów równoległych dwoma rozjazdami o jednakowym skosie (rys. 3.18).

Tyczenie rozpoczyna się od wyznaczenia punktów A₁, M₁ i P₁ wzdłuż osi toru 1.

Następnie wyznacza się punkt M₂ przez wystawienie prostopadłej d (rozstaw osi toru 1 i 2) z punktu B, leżącego na osi toru 1 w odległości b = n ⋅ d od punktu M₁.

Prawidłowość wyznaczenia punktu M₂ sprowadza się przez pomiar odcinka M₁ M₂. Odcinek ten powinien być równy wielkości określonej z wzoru

M₁ M₂ = d / sinα.

Po wytyczeniu punktu M₂ wyznacza się punkty A₂ i P₂, leżący na osi toru 2, w odległości a₂ i p₂ od punktu M₂. Pozostałe punkty (P'₁ i P'₂) wyznacza się przez odmierzenie wzdłuż prostej M₁ M₂ odcinków p₁' od punktu M₁ i p₂' od punktu M₂. Między punktami P'₁ i P'₂ powstanie prosta, której długość będzie równa

w = M₁ M₂ - (p'_{1 +} p'₂).

14

Tyczenie wskaźników konstrukcyjnych

Przed Tyczeniem wskaźników konstrukcyjnych należy założyć osnowę budowlano-montażową. Osnowa budowlano-montażowa służy do geodezyjnej obsługi poszczególnych etapów wznoszenia budowli (fundamenty, stan zerowy, kondygnacje powtarzalne).

Do tyczenia wskaźników konstrukcyjnych na kolejnych kondygnacjach powtarzalnych stosuje się, zależnie od przyjętej metody obsługi geodezyjnej, następujące rodzaje osnów:

3. osnowa budowlano- montażowa zewnętrzna (dla stanowisk teodolitu poza budynkiem) zakładana w celu tyczenia wskaźników metodą stałej prostej, rzutowania lub przecięć kierunków;

4. osnowa budowlano- montażowa wewnętrzna (dla instrumentu ustawionego na stropie budynku) wyznaczana za pomocą optycznych przyrządów do pionowania lub wyznaczania teodolitem metodą wtyczania się w określone kierunki.

Metoda biegunowa

Wskaźniki metodą biegunową tyczy się z punktów A i B przenoszonych na strop kondygnacji roboczej za pomocą pionowników, lub metodą przecięć kierunków opisaną poniżej.

Metoda polega na tym, że poszczególne punkty osi montażowych na kolejnych kondygnacjach wyznacza się przez odkładanie od punktów końcowych bazy i stałych kątów oraz odcinków wcześniej pomierzonych na poziomie zerowym. W tym celu na każdej kondygnacji nad punktami A_i i B_i ustawia się teodolit, który zawsze powinien być zorientowany na ten sam dobrze widoczny cel. Może to być punkt B jeżeli teodolit stoi na punkcie A i odwrotnie (patrz rys.1) , lub na dobrze widoczny cel jak np. antena (patrz rys.2). Następnie od kierunków np. AiBi, BiAi lub AiI, BiII, itd. Odkłada się kąty. Na wyznaczonych kierunkach odkłada się odcinki, których końce określają położenie punktów osiowych.

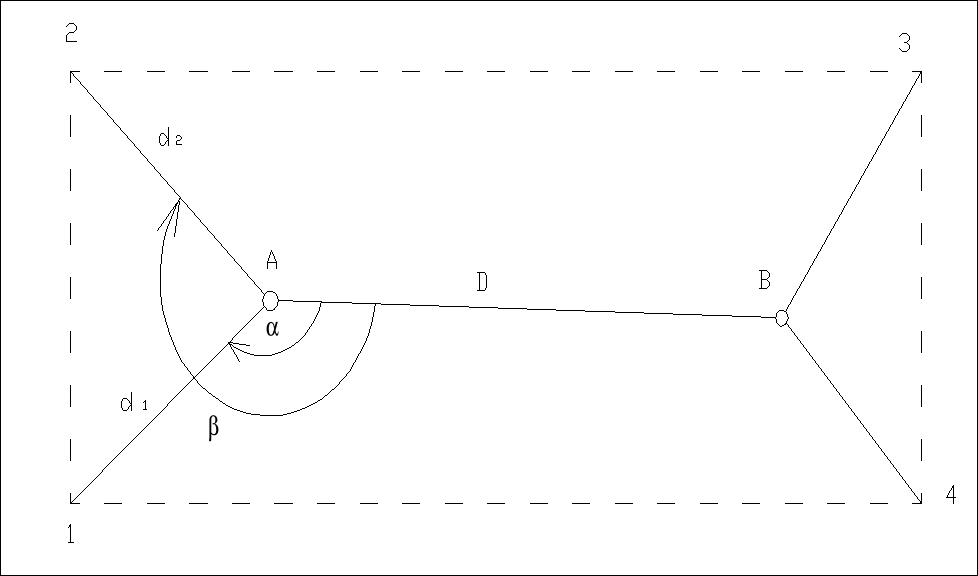
rys.1

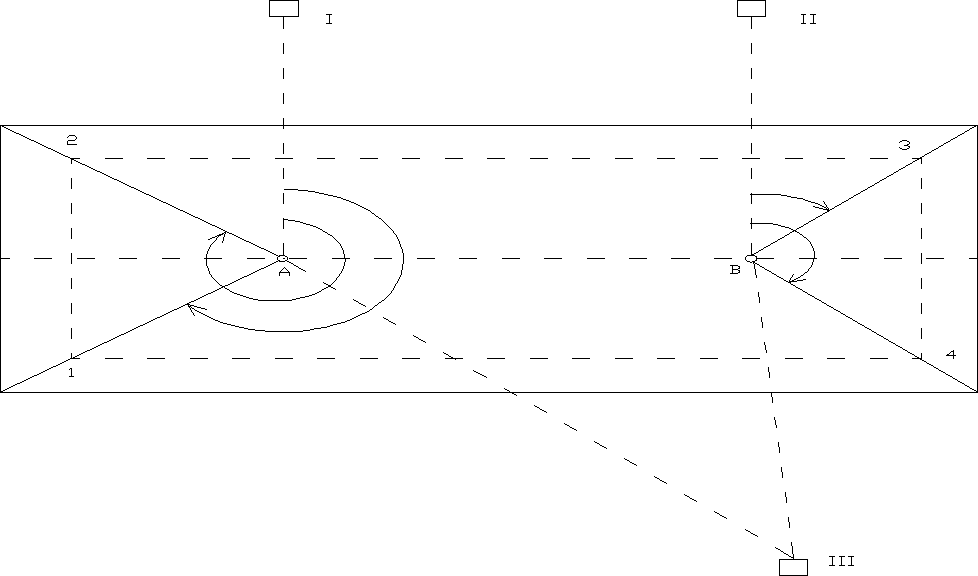
rys.2

Po wytyczeniu punktów nr. 1, 2

Kontrola pomiaru - pomiar 2

l_pom - l_obl = ?

l_obl² = d₁² +d₂² -2d₁d₂cos(-)

Analiza:

m_ = 3,7 mm, przy zał. m_ = m_ = 10^cc, m_d = 2 mm

m₁ = 0,3 mm (błąd centrowania pionownika)

m₃ = 0,1 mm (p = 20^cc/2 mm, h = 4 m, m₂ = 0,2p*h = 0,1 mm)

m_A = 1,6 mm (błąd przeniesienia pkt. A na wyższe kondygnacje)

Błąd metody m² = 3,7² + 1,6²

m =4 mm

Analiza dokładności metody biegunowej polega na porównaniu odcinka l_pom - odcinek między punktami osiowymi 1 i 2 na parterze ( chyba powinno się mówić: na stanie zerowym) z l_obl na kondygnacji.

Metoda przecięć kierunków

Metoda przecięć kierunków najczęściej stosowana jest do wyznaczenia osi stóp fundamentowych i wskaźników na półsłupkach parteru.

Wskaźniki konstrukcyjne tyczy się z osnowy budowlano-montażowej zewnętrznej.

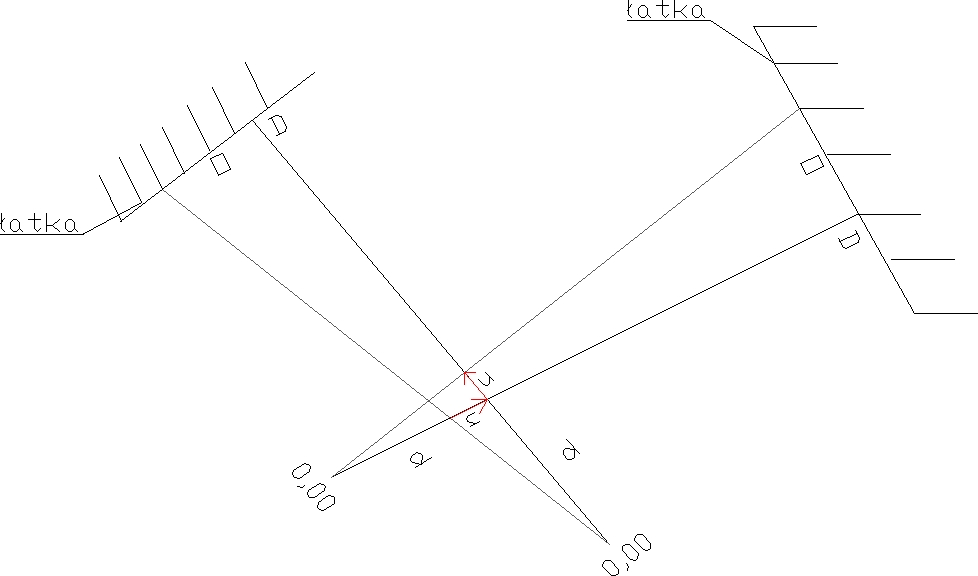
O₁/D₁=u/d₁

u=(O₁/D₁)*d₁

Np.

D₁=70m

d₁=30m

O₁=1m

u₁=0,43m

u₂=0,11m

D₂=80m

d₂=25m

O₂=0,35m

Metoda kolejnych przybliżeń

m=1,5mm

Wyznaczenie punktu A:

1. teodolit zorientowany na dobrze widoczny punkt np. antena,

2. odczyt z łatki,

(w dwóch położeniach lunety)

Ponowne ustawienie instrumentu na punkt A nie zawsze jest idealne i często myśląc, że stoimy na poprawnym punkcie tak naprawdę jesteśmy w pobliżu tego punktu tzn. na punkcie A'. Dlatego ponownie musimy zorientować teodolit na ten sam dobrze widoczny punkt i zrobić odczyt z łatki w dwóch położeniach. Następnie liczymy przesunięcie punktu A wykorzystując twierdzenie Talesa.

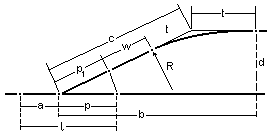
26. Budownictwo drogowe. Łuki pionowe, punkty główne i pośrednie.

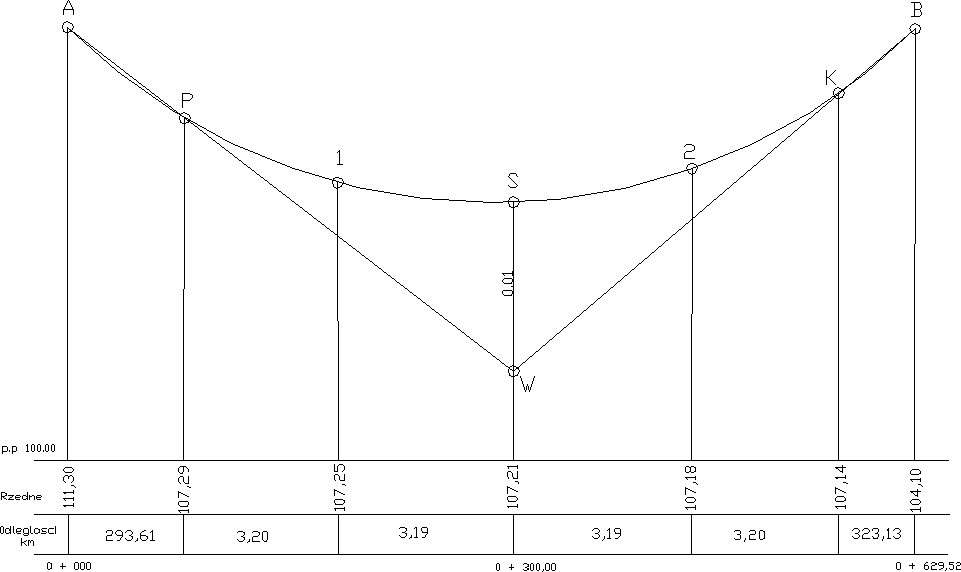
Nowo zaprojektowana niweleta drogi składa się z reguły z kilku niwelet o rożnych spadkach. Aby zachować prawidłowe warunki ruchu pojazdów na drodze, załamania niwelety płaszczyźnie pionowej powinny być złagodzone przez zastosowanie wyokrąglonych łuków pionowych. Jako łuki pionowe najczęściej stosuje się łuki kołowe lub symetryczne odcinki parabol. Łuki pionowe mogą być wklęsłe bądź wypukłe, w zależności od kierunku zmiany spadków niwelety.

Wytyczenie łuku pionowego podobnie jak poziomego, polega na wyznaczeniu w terenie punktów głównych i pośrednich łuku.

Spadek niwelety i₁=ΔH₁/D_{1 *} 100%

oraz i₂=ΔH₂/D_{2 *} 100%

styczna t do łuku pion.

t = R/2 (i₁+i₂); WS = t²/2R

Punkty pośrednie wyznaczono ze wzoru:

y_i ≈ x_i² / 2R

Obliczenie rzędnych ze wzorów

dla niwelety „pod górkę”

H = H_P + i_{1 *} x

dla niwelety „z górki”

H = H_k - i_{2 *} x

x - odl. danego p-tu od początku (lub końca) łuku.

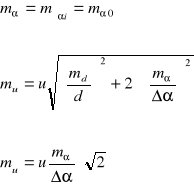
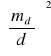
Jest bardzo małe i pomijamy

---